PHYS 415 OPTICS Review of Interference and Diffraction

PHYS 415: OPTICS Review of Interference and Diffraction F. ÖMER ILDAY Department of Physics, Bilkent University, Ankara, Turkey I used the following resources in the preparation of almost all these lectures: Trebino’s Modern Optics lectures from Gatech (quite heavily used), and various textbooks by Pedrotti & Pedrotti, Hecht, Guenther, Verdeyen, Fowles and Das www. bilkent. edu. tr/~ilday

Interference vs. Diffraction • Interference is when we add up multiple but a finite number of E&M waves • Diffraction is when we add up a continuum of E&M waves. • Fundamentally, there is no difference. www. bilkent. edu. tr/~ilday

Interference and Interferometers www. bilkent. edu. tr/~ilday

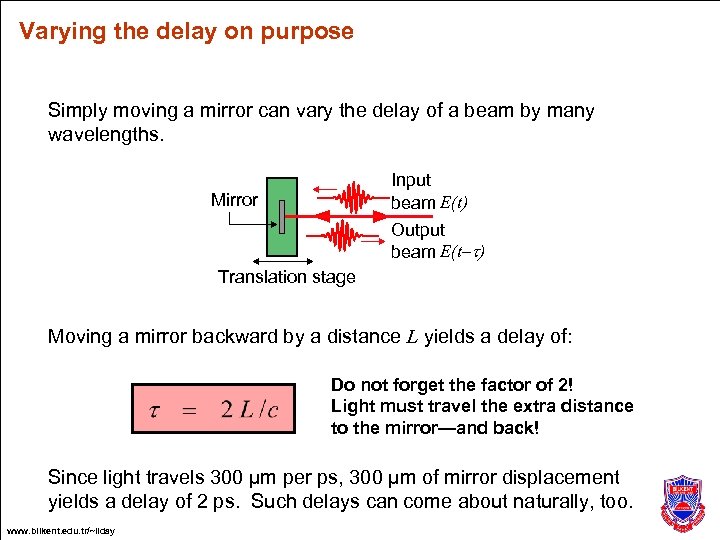Varying the delay on purpose Simply moving a mirror can vary the delay of a beam by many wavelengths. Input beam E(t) Mirror Output beam E(t–t) Translation stage Moving a mirror backward by a distance L yields a delay of: Do not forget the factor of 2! Light must travel the extra distance to the mirror—and back! Since light travels 300 µm per ps, 300 µm of mirror displacement yields a delay of 2 ps. Such delays can come about naturally, too. www. bilkent. edu. tr/~ilday

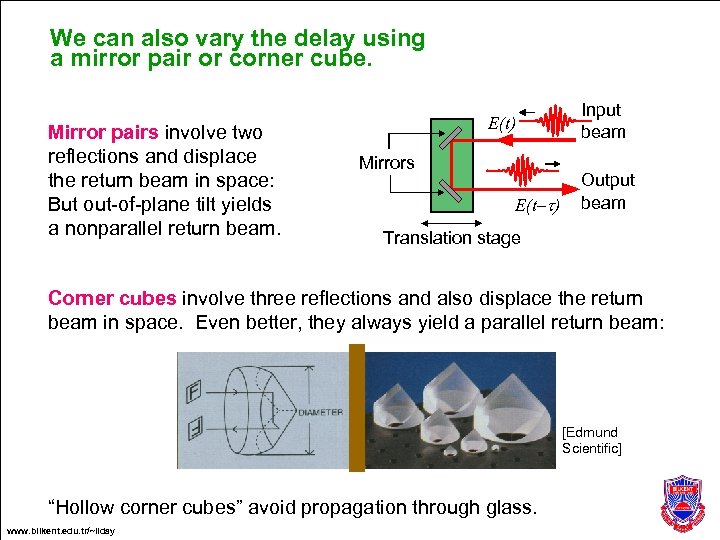We can also vary the delay using a mirror pair or corner cube. Mirror pairs involve two reflections and displace the return beam in space: But out-of-plane tilt yields a nonparallel return beam. E(t) Mirrors E(t–t) Input beam Output beam Translation stage Corner cubes involve three reflections and also displace the return beam in space. Even better, they always yield a parallel return beam: [Edmund Scientific] “Hollow corner cubes” avoid propagation through glass. www. bilkent. edu. tr/~ilday

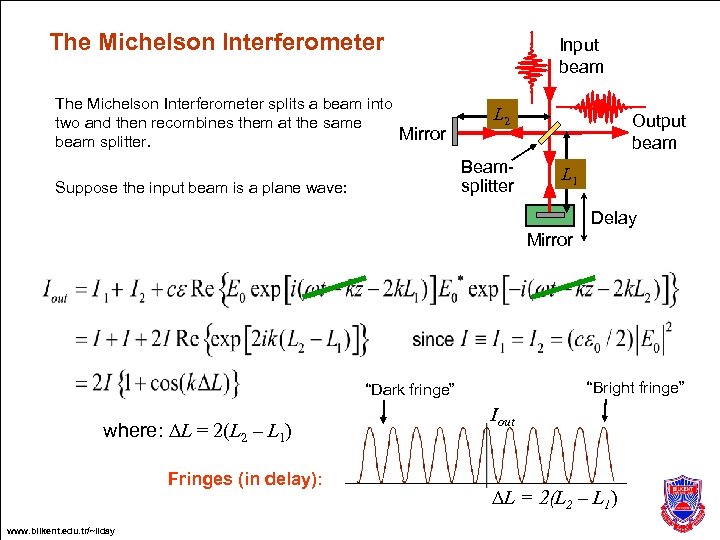The Michelson Interferometer splits a beam into two and then recombines them at the same Mirror beam splitter. Input beam L 2 Beamsplitter Suppose the input beam is a plane wave: Output beam L 1 Delay Mirror “Bright fringe” “Dark fringe” where: DL = 2(L 2 – L 1) Fringes (in delay): www. bilkent. edu. tr/~ilday Iout DL = 2(L 2 – L 1)

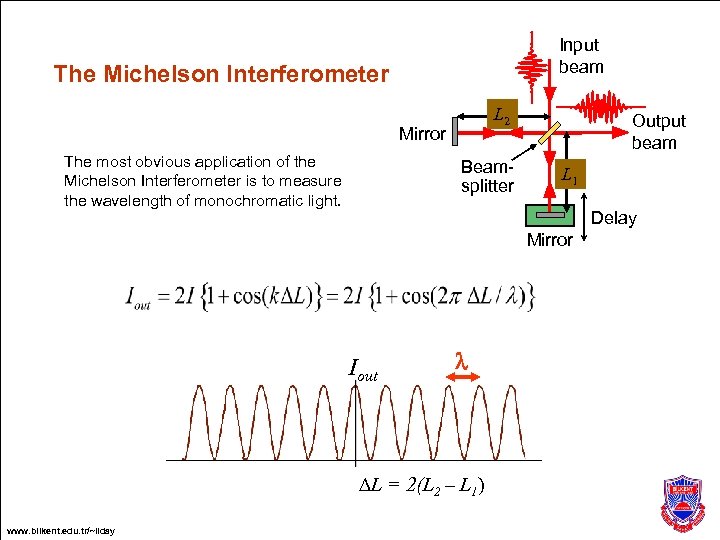Input beam The Michelson Interferometer L 2 Mirror The most obvious application of the Michelson Interferometer is to measure the wavelength of monochromatic light. Beamsplitter Output beam L 1 Delay Mirror Iout l DL = 2(L 2 – L 1) www. bilkent. edu. tr/~ilday

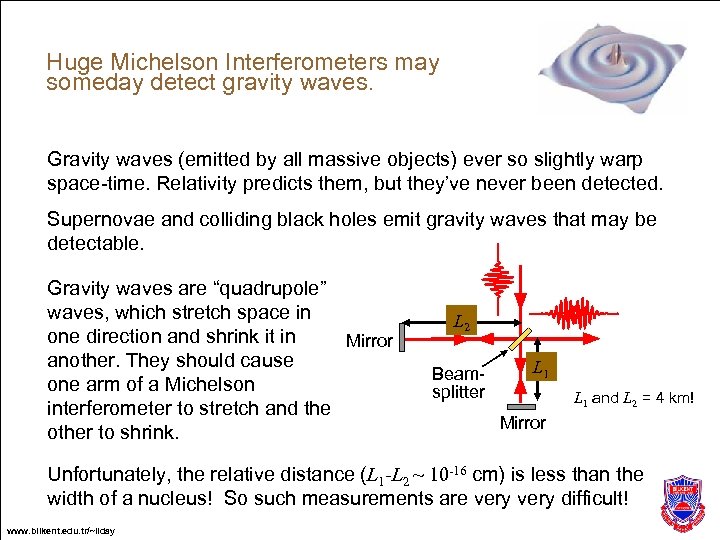Huge Michelson Interferometers may someday detect gravity waves. Gravity waves (emitted by all massive objects) ever so slightly warp space-time. Relativity predicts them, but they’ve never been detected. Supernovae and colliding black holes emit gravity waves that may be detectable. Gravity waves are “quadrupole” waves, which stretch space in one direction and shrink it in Mirror another. They should cause one arm of a Michelson interferometer to stretch and the other to shrink. L 2 Beamsplitter L 1 and L 2 = 4 km! Mirror Unfortunately, the relative distance (L 1 -L 2 ~ 10 -16 cm) is less than the width of a nucleus! So such measurements are very difficult! www. bilkent. edu. tr/~ilday

The LIGO project Cal. Tech LIGO The building containing an arm A small fraction of one arm of the Cal. Tech LIGO interferometer… Hanford LIGO The control center www. bilkent. edu. tr/~ilday

The LIGO folks think big… The longer the interferometer arms, the better the sensitivity. So put one in space, of course. www. bilkent. edu. tr/~ilday

The Michelson Interferometer is a Fourier Transform Spectrometer L 2 Suppose the input beam is not monochromatic (but is perfectly spatially coherent): Þ Iout = 2 I + c e Re{E(t+2 L 1 /c) E*(t+2 L 2 /c)} Beamsplitter L 1 Now, Iout will vary rapidly in time, and most detectors will simply integrate over Mirror a relatively long time, T : Delay Changing variables: t' = t + 2 L 1 /c and letting t = 2(L 2 - L 1)/c and T ® ¥ The Field Autocorrelation! Recall that the Fourier Transform of the Field Autocorrelation is the spectrum!! www. bilkent. edu. tr/~ilday

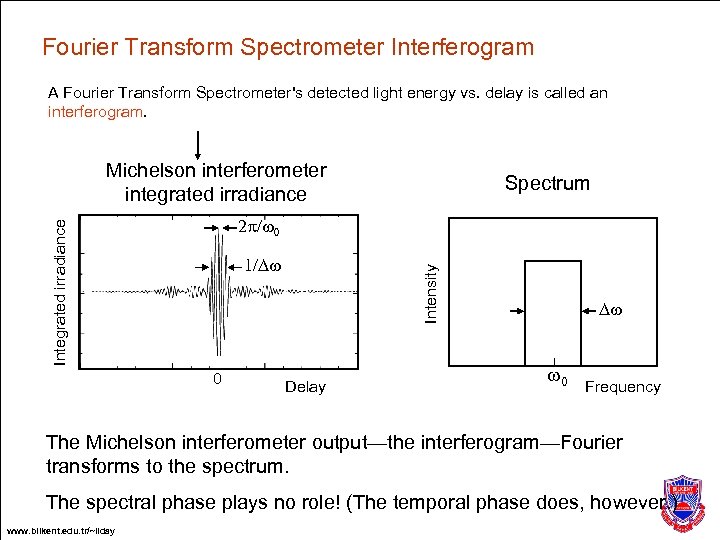Fourier Transform Spectrometer Interferogram A Fourier Transform Spectrometer's detected light energy vs. delay is called an interferogram. Michelson interferometer integrated irradiance Spectrum Integrated irradiance 2 p/w 0 0 Intensity 1/Dw Delay Dw w 0 Frequency The Michelson interferometer output—the interferogram—Fourier transforms to the spectrum. The spectral phase plays no role! (The temporal phase does, however. ) www. bilkent. edu. tr/~ilday

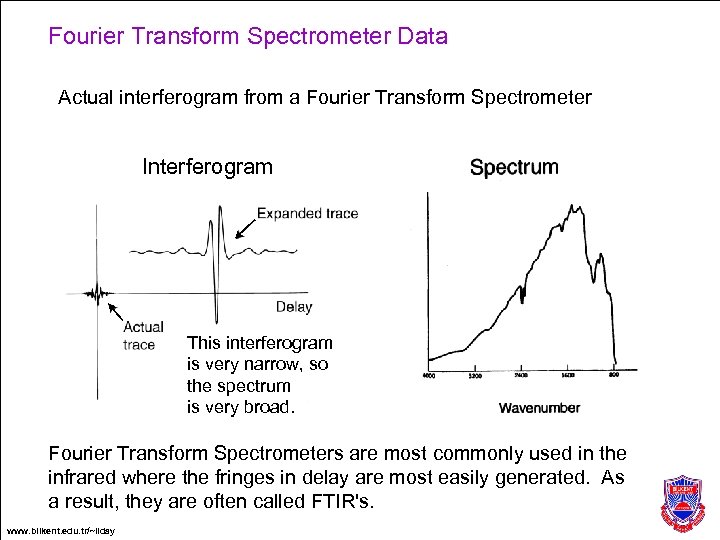Fourier Transform Spectrometer Data Actual interferogram from a Fourier Transform Spectrometer Interferogram This interferogram is very narrow, so the spectrum is very broad. Fourier Transform Spectrometers are most commonly used in the infrared where the fringes in delay are most easily generated. As a result, they are often called FTIR's. www. bilkent. edu. tr/~ilday

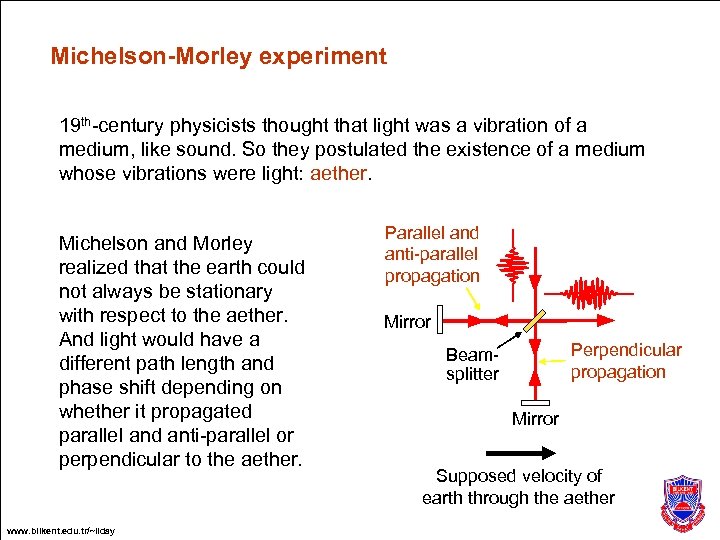Michelson-Morley experiment 19 th-century physicists thought that light was a vibration of a medium, like sound. So they postulated the existence of a medium whose vibrations were light: aether. Michelson and Morley realized that the earth could not always be stationary with respect to the aether. And light would have a different path length and phase shift depending on whether it propagated parallel and anti-parallel or perpendicular to the aether. www. bilkent. edu. tr/~ilday Parallel and anti-parallel propagation Mirror Perpendicular propagation Beamsplitter Mirror Supposed velocity of earth through the aether

Michelson-Morley Experiment: Results The Michelson interferometer was (and may still be) the most sensitive measure of distance (or time) ever invented and should’ve revealed a fringe shift as it was rotated with respect to the aether velocity. Interference fringes showed no change as the interferometer was rotated. Their apparatus Michelson and Morley's results from A. A. Michelson, Studies in Optics www. bilkent. edu. tr/~ilday

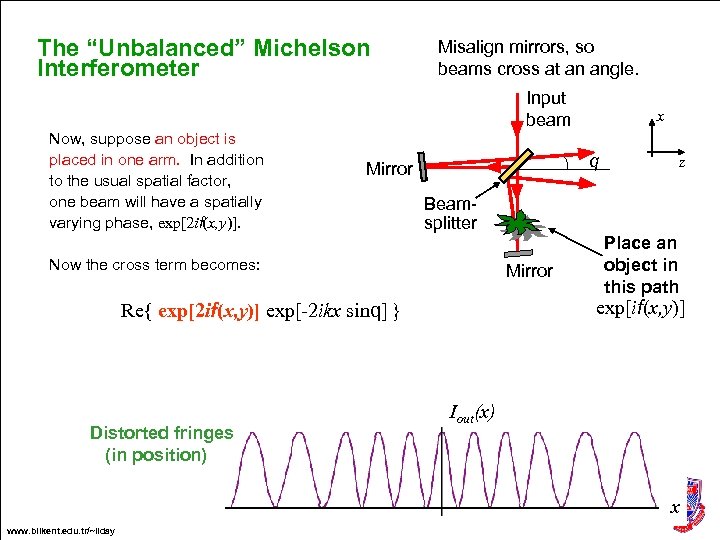The “Unbalanced” Michelson Interferometer Now, suppose an object is placed in one arm. In addition to the usual spatial factor, one beam will have a spatially varying phase, exp[2 if(x, y)]. Misalign mirrors, so beams cross at an angle. Input beam q Mirror z Beamsplitter Now the cross term becomes: Mirror Place an object in this path exp[if(x, y)] Re{ exp[2 if(x, y)] exp[-2 ikx sinq] } Distorted fringes (in position) x Iout(x) x www. bilkent. edu. tr/~ilday

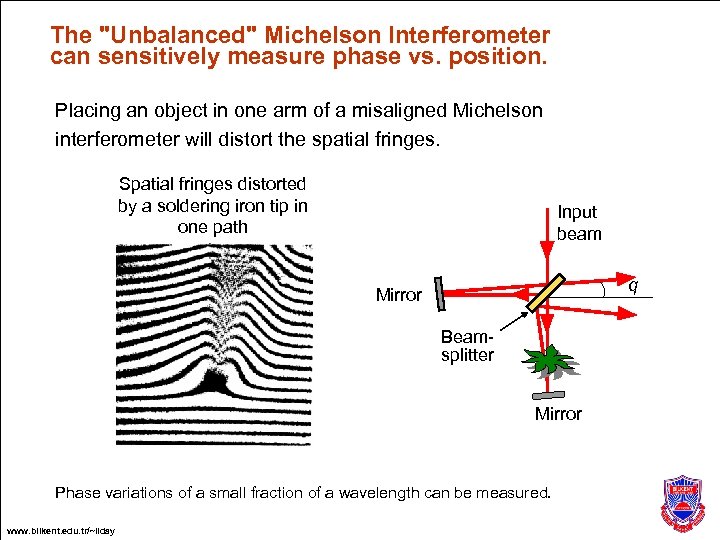The "Unbalanced" Michelson Interferometer can sensitively measure phase vs. position. Placing an object in one arm of a misaligned Michelson interferometer will distort the spatial fringes. Spatial fringes distorted by a soldering iron tip in one path Input beam q Mirror Beamsplitter Mirror Phase variations of a small fraction of a wavelength can be measured. www. bilkent. edu. tr/~ilday

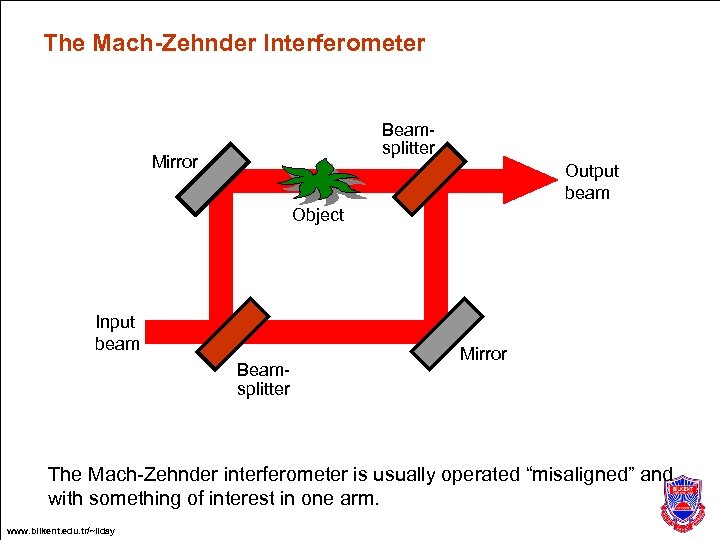The Mach-Zehnder Interferometer Beamsplitter Mirror Output beam Object Input beam Beamsplitter Mirror The Mach-Zehnder interferometer is usually operated “misaligned” and with something of interest in one arm. www. bilkent. edu. tr/~ilday

Mach-Zehnder Interferogram Nothing in either path www. bilkent. edu. tr/~ilday Plasma in one path

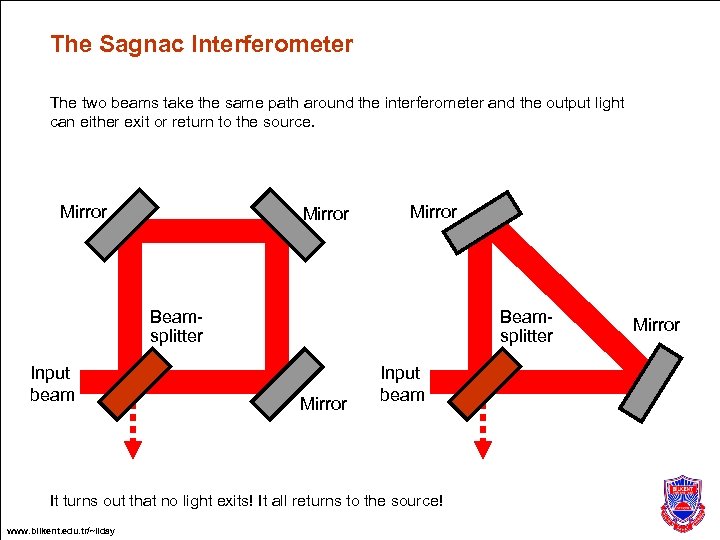The Sagnac Interferometer The two beams take the same path around the interferometer and the output light can either exit or return to the source. Mirror Beamsplitter Input beam Beamsplitter Mirror Input beam It turns out that no light exits! It all returns to the source! www. bilkent. edu. tr/~ilday Mirror

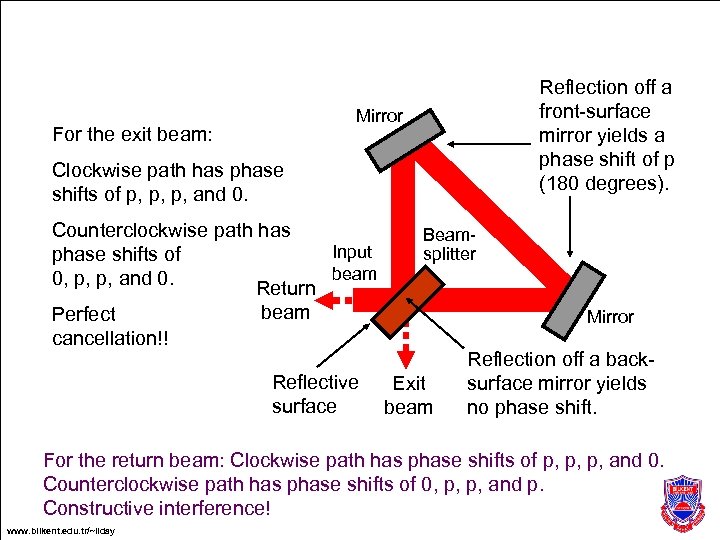Why all the light returns to the source in a Sagnac interferometer Reflection off a front-surface mirror yields a phase shift of p (180 degrees). Mirror For the exit beam: Clockwise path has phase shifts of p, p, p, and 0. Counterclockwise path has Input phase shifts of beam 0, p, p, and 0. Return beam Perfect cancellation!! Beamsplitter Reflective Exit surface beam Mirror Reflection off a backsurface mirror yields no phase shift. For the return beam: Clockwise path has phase shifts of p, p, p, and 0. Counterclockwise path has phase shifts of 0, p, p, and p. Constructive interference! www. bilkent. edu. tr/~ilday

The Sagnac Interferometer senses rotation Suppose that the beam splitter moves by a distance, d, in the time, T, it takes light to circumnavigate the Sagnac interferometer. As a result, one beam will travel more, and the other less distance. If R = the interferometer radius, and W = its angular velocity: R d d = Rq q Sagnac Interfer ometer q = WT Thus, the Sagnac Interferometer's sensitivity to rotation depends on its area. And it need not be round! www. bilkent. edu. tr/~ilday

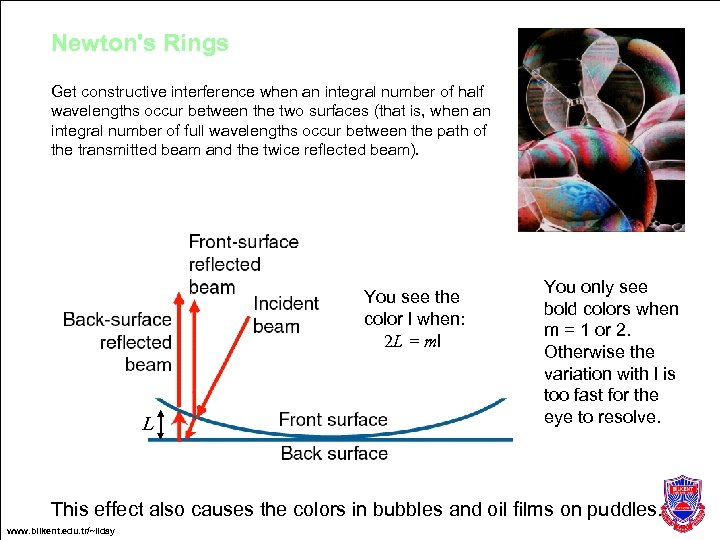Newton's Rings Get constructive interference when an integral number of half wavelengths occur between the two surfaces (that is, when an integral number of full wavelengths occur between the path of the transmitted beam and the twice reflected beam). You see the color l when: 2 L = ml L You only see bold colors when m = 1 or 2. Otherwise the variation with l is too fast for the eye to resolve. This effect also causes the colors in bubbles and oil films on puddles. www. bilkent. edu. tr/~ilday

Newton's Rings www. bilkent. edu. tr/~ilday

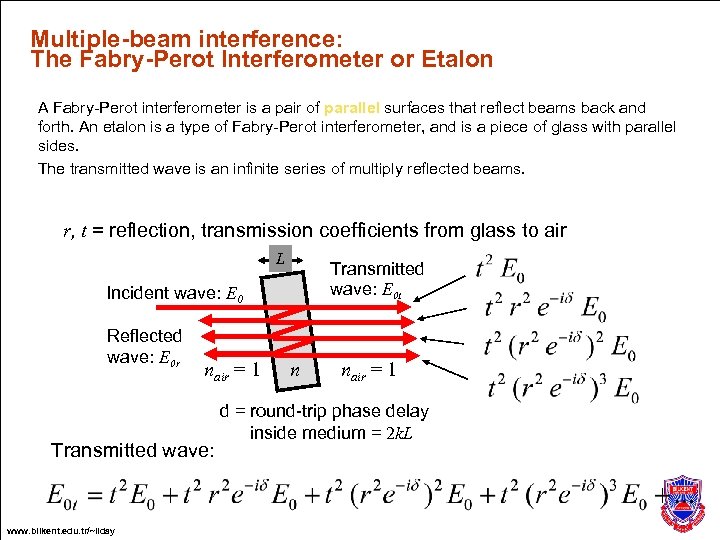Multiple-beam interference: The Fabry-Perot Interferometer or Etalon A Fabry-Perot interferometer is a pair of parallel surfaces that reflect beams back and forth. An etalon is a type of Fabry-Perot interferometer, and is a piece of glass with parallel sides. The transmitted wave is an infinite series of multiply reflected beams. r, t = reflection, transmission coefficients from glass to air L Transmitted wave: E 0 t Incident wave: E 0 Reflected wave: E 0 r nair = 1 Transmitted wave: www. bilkent. edu. tr/~ilday n nair = 1 d = round-trip phase delay inside medium = 2 k. L

The Etalon (cont'd) The transmitted wave field is: The transmittance is: Dividing numerator and denominator by where: www. bilkent. edu. tr/~ilday

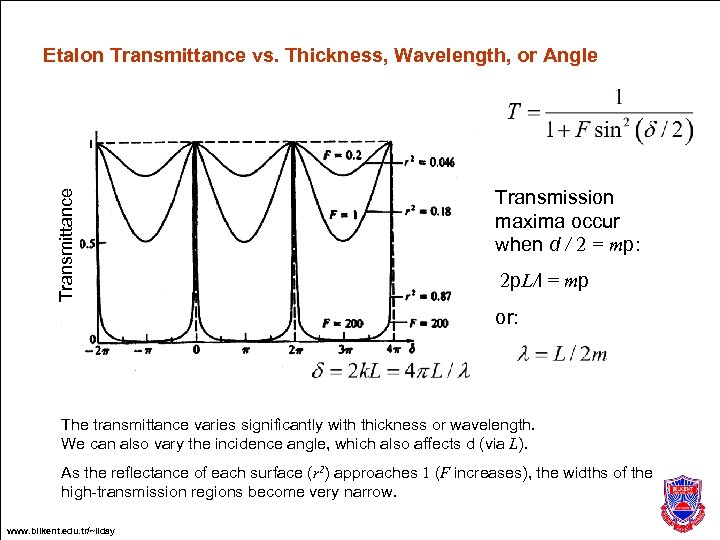Transmittance Etalon Transmittance vs. Thickness, Wavelength, or Angle Transmission maxima occur when d / 2 = mp: 2 p. L/l = mp or: The transmittance varies significantly with thickness or wavelength. We can also vary the incidence angle, which also affects d (via L). As the reflectance of each surface (r 2) approaches 1 (F increases), the widths of the high-transmission regions become very narrow. www. bilkent. edu. tr/~ilday

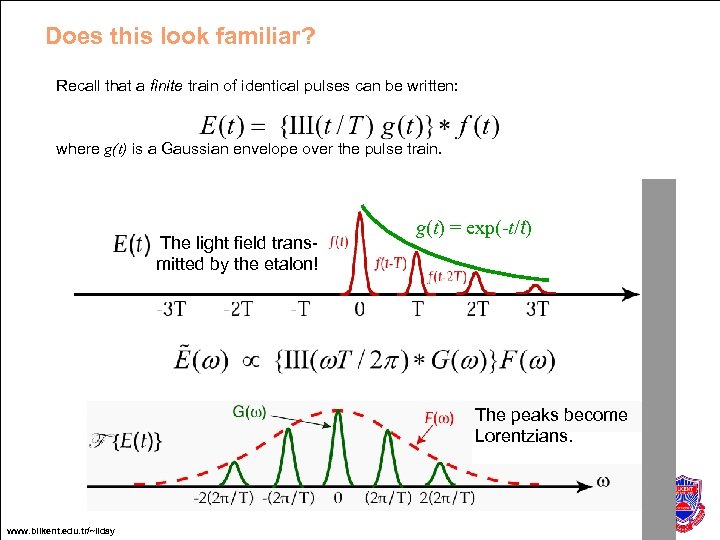Does this look familiar? Recall that a finite train of identical pulses can be written: where g(t) is a Gaussian envelope over the pulse train. The light field transmitted by the etalon! g(t) = exp(-t/t) The peaks become Lorentzians. www. bilkent. edu. tr/~ilday

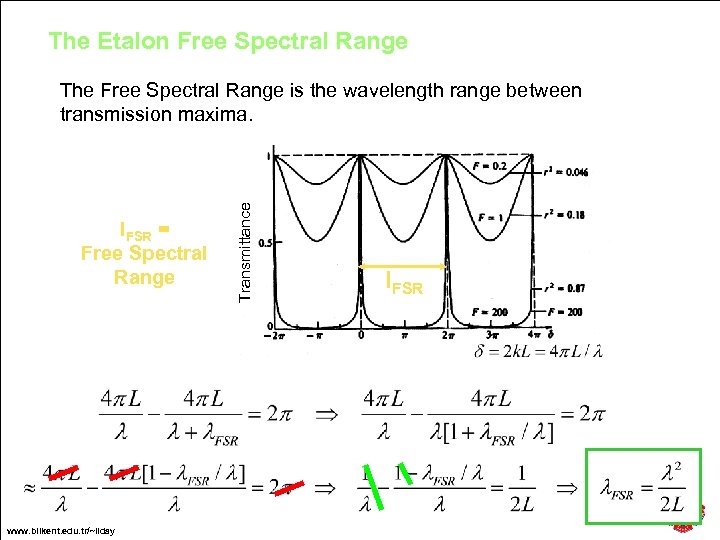The Etalon Free Spectral Range l. FSR = Free Spectral Range www. bilkent. edu. tr/~ilday Transmittance The Free Spectral Range is the wavelength range between transmission maxima. l. FSR

Etalon Linewidth The Linewidth d. LW is a transmittance peak's full-width-half-max (FWHM). Transmittance Setting d equal to d. LW/2 should yield T = 1/2: For d << 1, we can make the small argument approx: Substituting Or: www. bilkent. edu. tr/~ilday l. LW l and we have: The linewidth is the etalon’s wavelength-measurement accuracy.

The Interferometer or Etalon Finesse The Finesse, F , is the ratio of the Free Spectral Range and the Linewidth: Taking The Finesse is the number of wavelengths the interferometer can resolve. www. bilkent. edu. tr/~ilday

How to use an interferometer to measure wavelength 1. Measure the wavelength to within one Free Spectral Range using a grating or prism spectrometer to avoid the interferometer’s inherent ambiguities. 2. Scan the spacing of the two mirrors and record the spacing when a transmission maximum occurs. 3. If greater accuracy is required, use another (longer) interferometer with a FSR ~ the above accuracy (line-width) and with an even smaller line-width (i. e. , better accuracy). Interferometers are the most accurate measures of wavelength available. www. bilkent. edu. tr/~ilday

Anti-reflection Coating Notice that the center of the round glass plate looks like it’s missing. It’s not! There’s an “anti -reflection coating” there (on both the front and back of the glass). www. bilkent. edu. tr/~ilday

Anti-reflection Coating Math Consider a beam incident on a piece of glass (n = ns) with a layer of material (n = nl) if thickness, h, on its surface. It can be shown that the Reflectance is (for such thin media, we need to go back to Maxwell’s equations): Notice that R = 0 if: www. bilkent. edu. tr/~ilday

Multilayer coatings Typical laser mirrors and camera lenses use many layers. The reflectance and transmittance can be tailored to taste! www. bilkent. edu. tr/~ilday

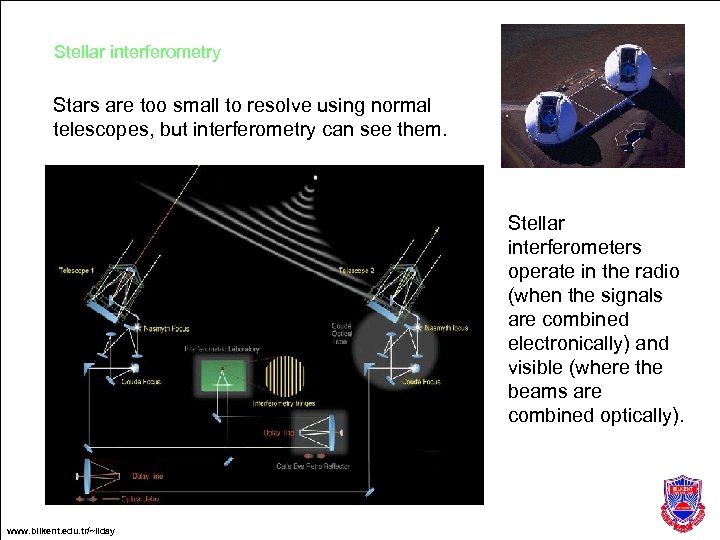Stellar interferometry Stars are too small to resolve using normal telescopes, but interferometry can see them. Stellar interferometers operate in the radio (when the signals are combined electronically) and visible (where the beams are combined optically). Taken from von der Luhe, of Kiepenheuer-Institut fur Sonnenphysik, Freiburg, Germany. www. bilkent. edu. tr/~ilday

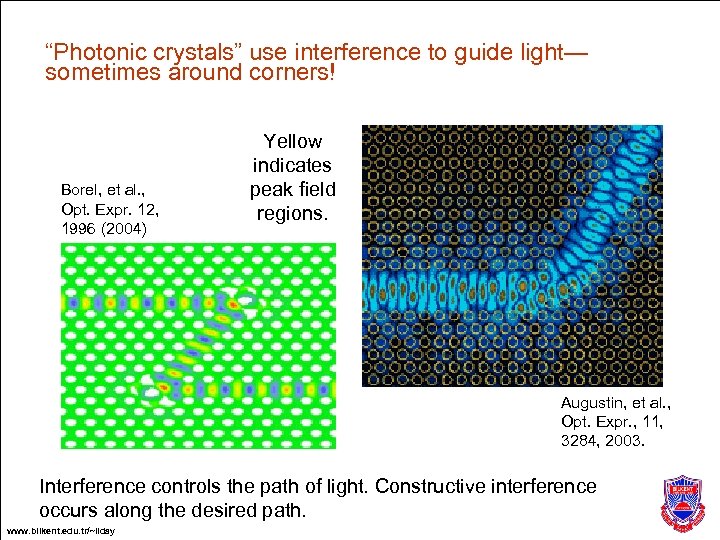“Photonic crystals” use interference to guide light— sometimes around corners! Borel, et al. , Opt. Expr. 12, 1996 (2004) Yellow indicates peak field regions. Augustin, et al. , Opt. Expr. , 11, 3284, 2003. Interference controls the path of light. Constructive interference occurs along the desired path. www. bilkent. edu. tr/~ilday

Convolution www. bilkent. edu. tr/~ilday

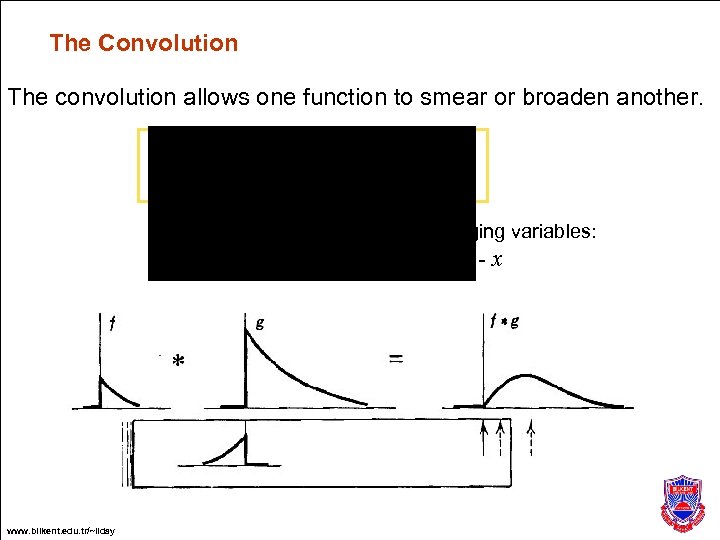The Convolution The convolution allows one function to smear or broaden another. changing variables: x t - x www. bilkent. edu. tr/~ilday

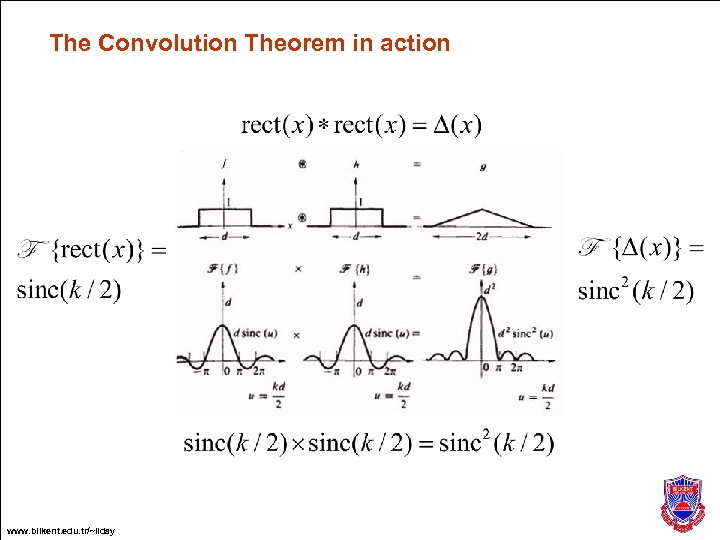
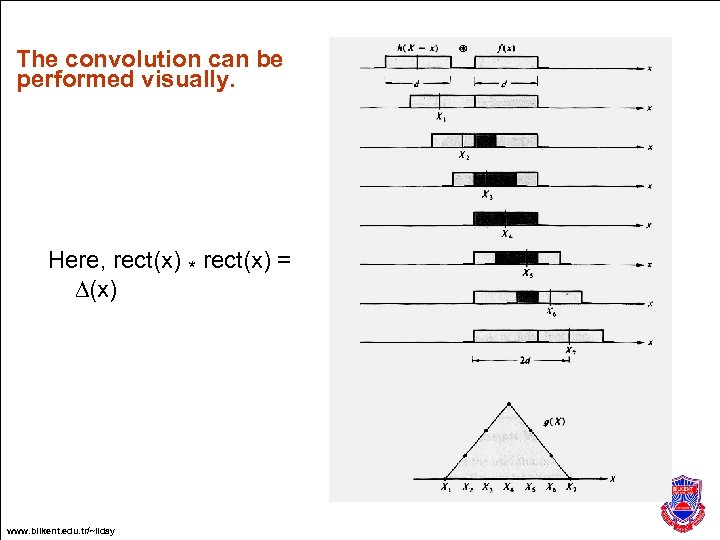The convolution can be performed visually. Here, rect(x) * rect(x) = D(x) www. bilkent. edu. tr/~ilday

Convolution with a delta function simply centers the function on the delta-function. This convolution does not smear out f(t). Since a device’s performance can usually be described as a convolution of the quantity it’s trying to measure and some instrument response, a perfect device has a delta-function instrument www. bilkent. edu. tr/~ilday

The Convolution Theorem turns a convolution into the inverse FT of the product of the Fourier Transforms: Proof: www. bilkent. edu. tr/~ilday

The Convolution Theorem in action www. bilkent. edu. tr/~ilday

The Shah Function The Shah function, III(t), is an infinitely long train of equally spaced delta-functions. t The symbol III is pronounced shah after the Cyrillic character III, which is said to have been modeled on the Hebrew letter (shin) which, in turn, may derive from the Egyptian a hieroglyph depicting papyrus plants along the Nile. www. bilkent. edu. tr/~ilday

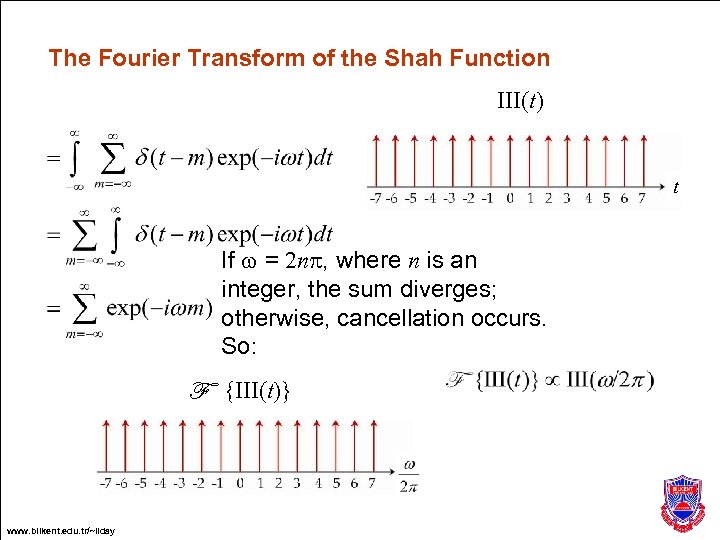The Fourier Transform of the Shah Function III(t) t If w = 2 np, where n is an integer, the sum diverges; otherwise, cancellation occurs. So: F {III(t)} www. bilkent. edu. tr/~ilday

Fraunhofer Diffraction www. bilkent. edu. tr/~ilday

Diffraction Light does not always travel in a straight line. It tends to bend around objects. This tendency is called diffraction. Shadow of a hand illuminated by a Helium. Neon laser Any wave will do this, including matter waves and acoustic waves. Shadow of a zinc oxide crystal illuminated by a electrons www. bilkent. edu. tr/~ilday

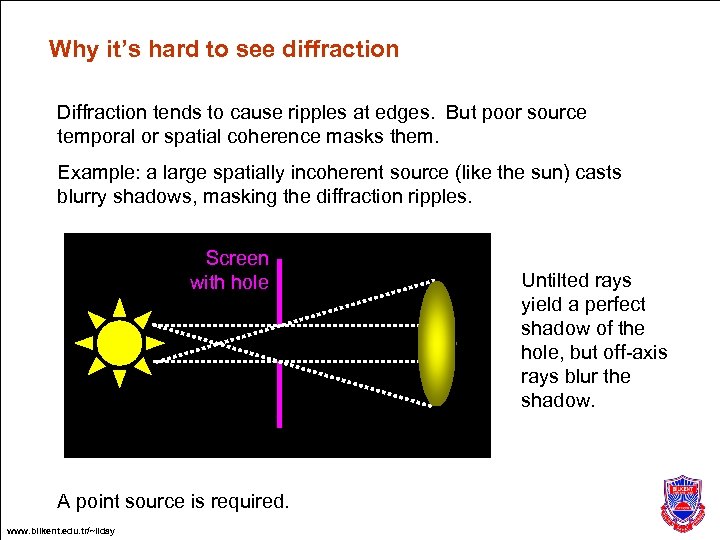Why it’s hard to see diffraction Diffraction tends to cause ripples at edges. But poor source temporal or spatial coherence masks them. Example: a large spatially incoherent source (like the sun) casts blurry shadows, masking the diffraction ripples. Screen with hole A point source is required. www. bilkent. edu. tr/~ilday Untilted rays yield a perfect shadow of the hole, but off-axis rays blur the shadow.

Diffraction of a wave by a slit Whether waves in water or electromagnetic radiation in air, passage through a slit yields a diffraction pattern that will appear more dramatic as the size of the slit approaches the wavelength of the wave. www. bilkent. edu. tr/~ilday

Diffraction of ocean water waves Ocean waves passing through slits in Tel Aviv, Israel Diffraction occurs for all waves, whatever the phenomenon. www. bilkent. edu. tr/~ilday

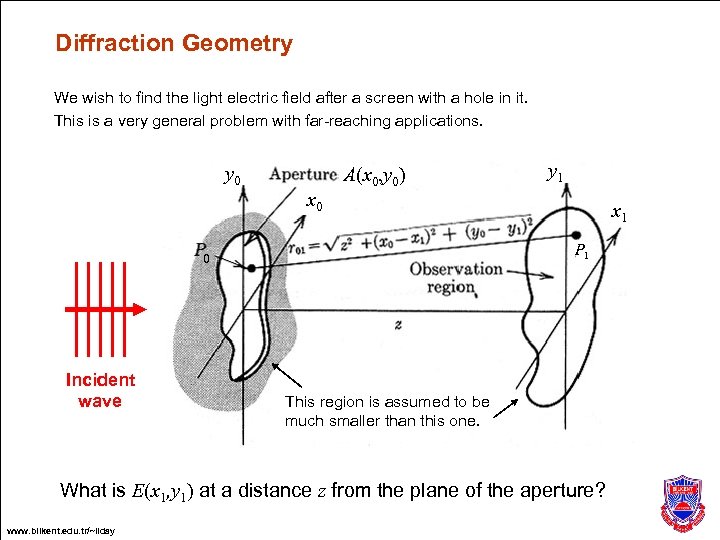Diffraction Geometry We wish to find the light electric field after a screen with a hole in it. This is a very general problem with far-reaching applications. y 0 A(x 0, y 0) y 1 x 0 P 1 0 Incident wave x 1 This region is assumed to be much smaller than this one. What is E(x 1, y 1) at a distance z from the plane of the aperture? www. bilkent. edu. tr/~ilday

Diffraction Solution The field in the observation plane, E(x 1, y 1), at a distance z from the aperture plane is given by a convolution: A very complicated result! And we cannot approximate r 01 in the exp by z because it gets multiplied by k, which is big, so relatively small changes in r 01 can make a big difference! www. bilkent. edu. tr/~ilday

Fraunhofer Diffraction: The Far Field Recall the Fresnel diffraction result: Let D be the size of the aperture: D 2 = x 02 + y 02. When k. D 2/2 z << 1, the quadratic terms << 1, so we can neglect them: This condition corresponds to going far away: z >> k. D 2/2 = p. D 2/l If D = 100 microns and l = 1 micron, then z >> 30 meters, which is far! www. bilkent. edu. tr/~ilday

Fraunhofer Diffraction Conventions As in Fresnel diffraction, we’ll neglect the phase factors, and we’ll explicitly write the aperture function in the integral: This is just a Fourier Transform! E(x 0, y 0) = constant if a plane wave Interestingly, it’s a Fourier Transform from position, x 0, to another position variable, x 1 (in another plane). Usually, the Fourier “conjugate variables” have reciprocal units (e. g. , t & w, or x & k). The conjugate variables here are really x 0 and kx = kx 1/z, which have reciprocal units. So the far-field light field is the Fourier Transform of the apertured field! www. bilkent. edu. tr/~ilday

The Fraunhofer Diffraction formula We can write this result in terms of the off-axis k-vector components: E(x, y) = const if a plane wave Aperture function where we’ve dropped the subscripts, 0 and 1, kx = kx 1/z and ky = ky 1/z and: kx kz or: qx = kx /k = x 1/z and qy = ky /k = y 1/z www. bilkent. edu. tr/~ilday ky

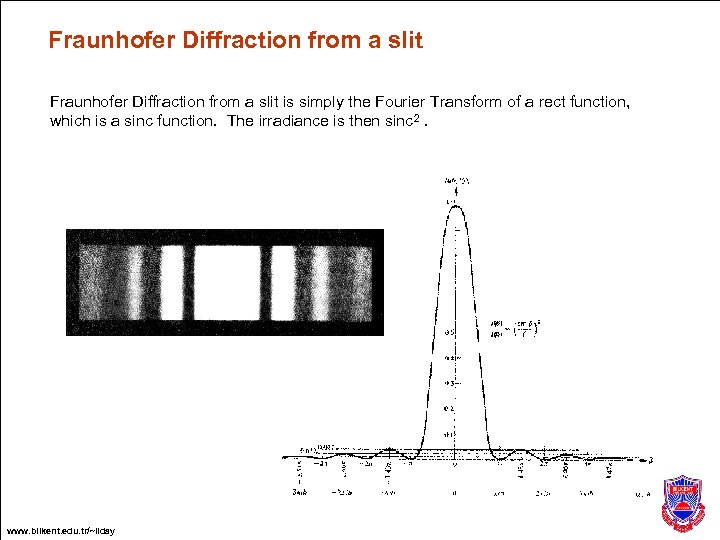Fraunhofer Diffraction from a slit is simply the Fourier Transform of a rect function, which is a sinc function. The irradiance is then sinc 2. www. bilkent. edu. tr/~ilday

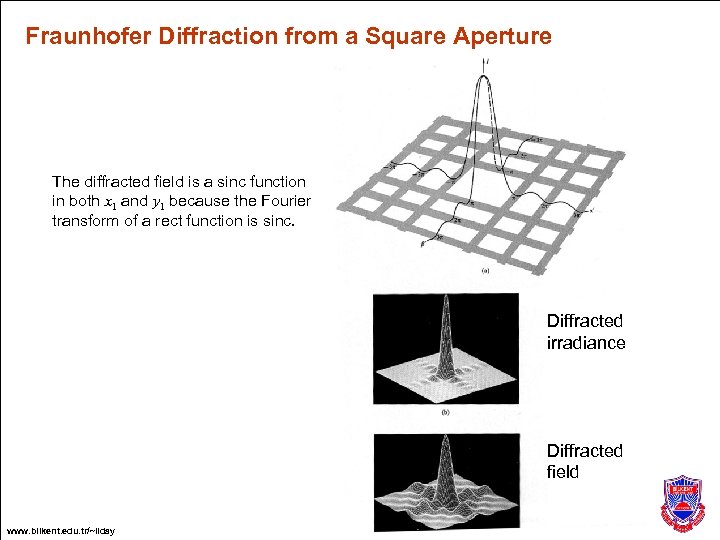Fraunhofer Diffraction from a Square Aperture The diffracted field is a sinc function in both x 1 and y 1 because the Fourier transform of a rect function is sinc. Diffracted irradiance Diffracted field www. bilkent. edu. tr/~ilday

Diffraction from a Circular Aperture A circular aperture yields a diffracted "Airy Pattern, " which involves a Bessel function. Diffracted Irradiance Diffracted field www. bilkent. edu. tr/~ilday

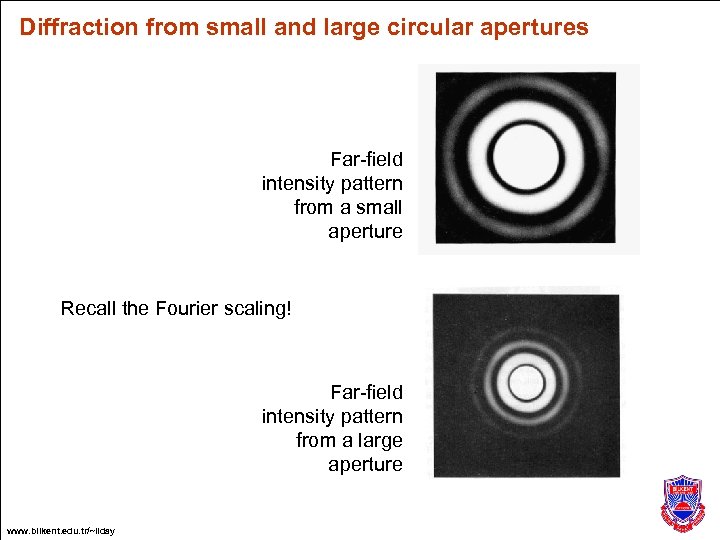Diffraction from small and large circular apertures Far-field intensity pattern from a small aperture Recall the Fourier scaling! Far-field intensity pattern from a large aperture www. bilkent. edu. tr/~ilday

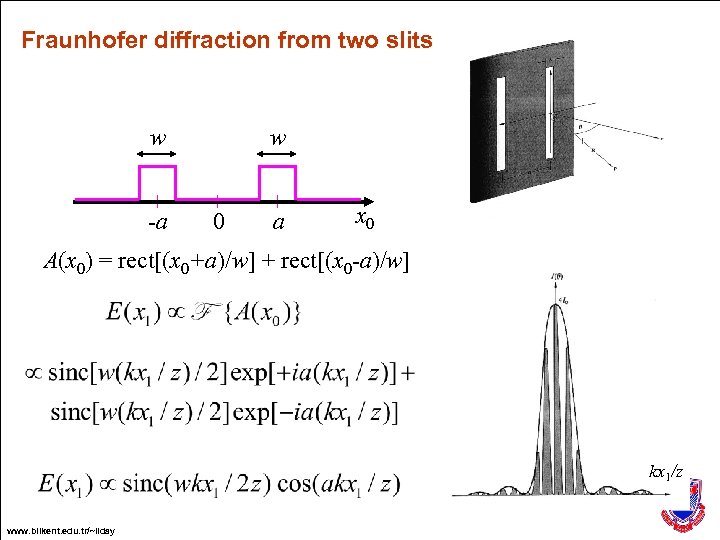Fraunhofer diffraction from two slits w -a w 0 a x 0 A(x 0) = rect[(x 0+a)/w] + rect[(x 0 -a)/w] kx 1/z www. bilkent. edu. tr/~ilday

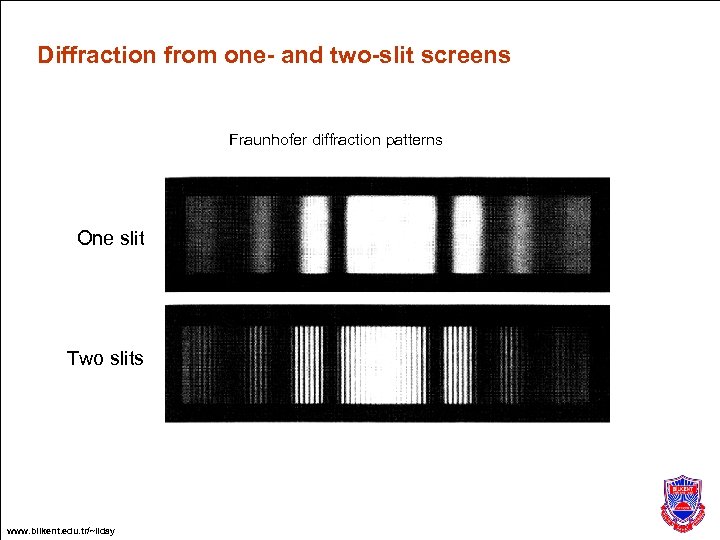Diffraction from one- and two-slit screens Fraunhofer diffraction patterns One slit Two slits www. bilkent. edu. tr/~ilday

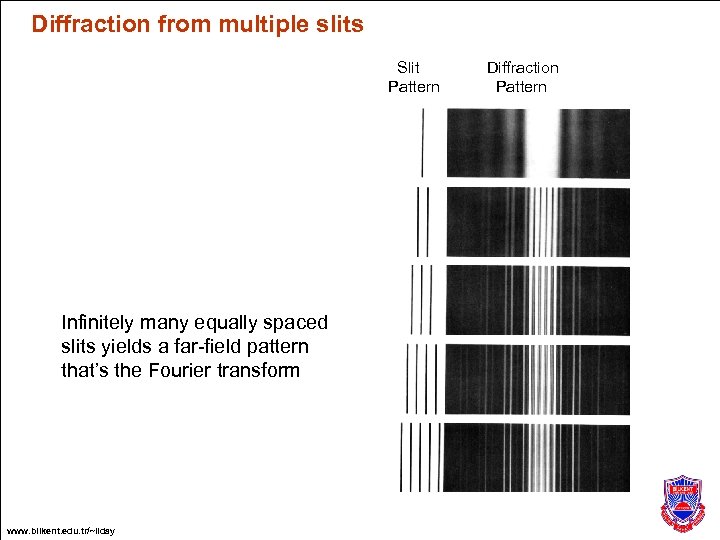Diffraction from multiple slits Slit Pattern Infinitely many equally spaced slits yields a far-field pattern that’s the Fourier transform www. bilkent. edu. tr/~ilday Diffraction Pattern

Young’s Two Slit Experiment and Quantum Mechanics Imagine using a beam so weak that only one photon passes through the screen at a time. In this case, the photon would seem to pass through only one slit at a time, yielding a one-slit pattern. Which pattern occurs? Possible Fraunhofer diffraction patterns Each photon passes through only one slit Each photon passes through both slits www. bilkent. edu. tr/~ilday

Fresnel Diffraction www. bilkent. edu. tr/~ilday

Fresnel Diffraction: Approximations But, in the denominator, we can approximate r 01 by z. And, in the numerator, we can write: This yields: www. bilkent. edu. tr/~ilday

Fresnel Diffraction: Approximations Multiplying out the squares: Factoring out the quantities independent of x 0 and y 0: This is the Fresnel integral. It's complicated! It yields the light wave field at the distance z from the screen. www. bilkent. edu. tr/~ilday

Diffraction Conventions We’ll typically assume that a plane wave is incident on the aperture. It still has an exp[i(w t – k z)], but it’s constant with respect to x 0 and y 0. And we’ll explicitly write the aperture function in the integral: And we’ll usually ignore the various factors in front: www. bilkent. edu. tr/~ilday

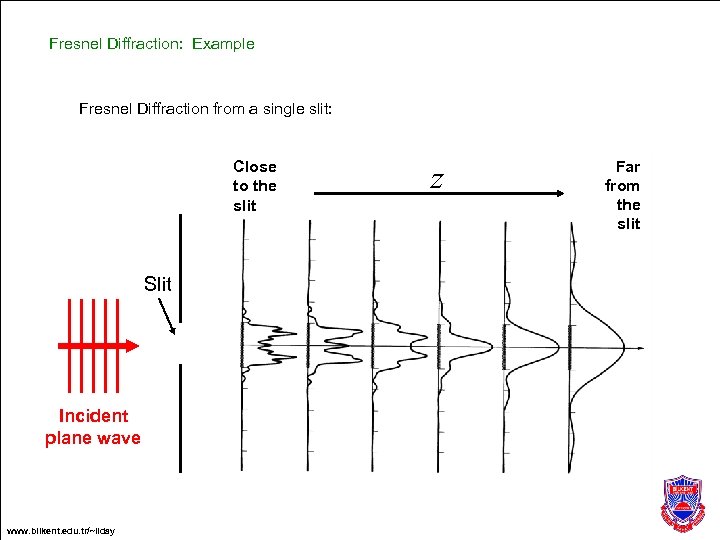Fresnel Diffraction: Example Fresnel Diffraction from a single slit: Close to the slit Slit Incident plane wave www. bilkent. edu. tr/~ilday z Far from the slit

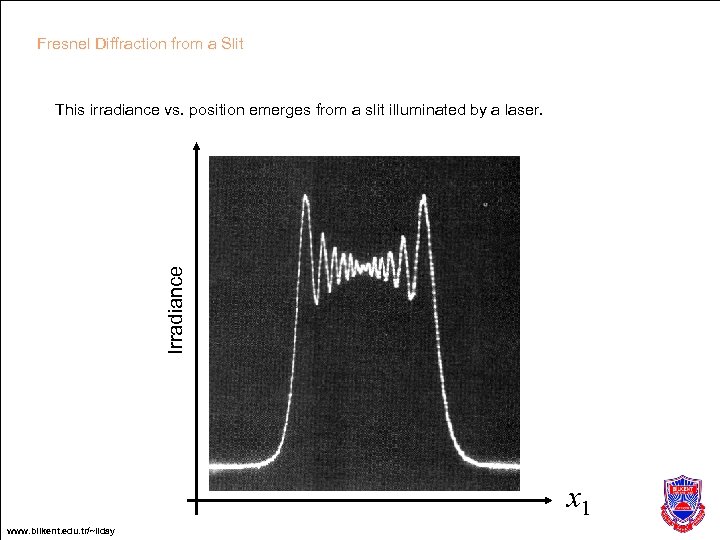Fresnel Diffraction from a Slit Irradiance This irradiance vs. position emerges from a slit illuminated by a laser. x 1 www. bilkent. edu. tr/~ilday

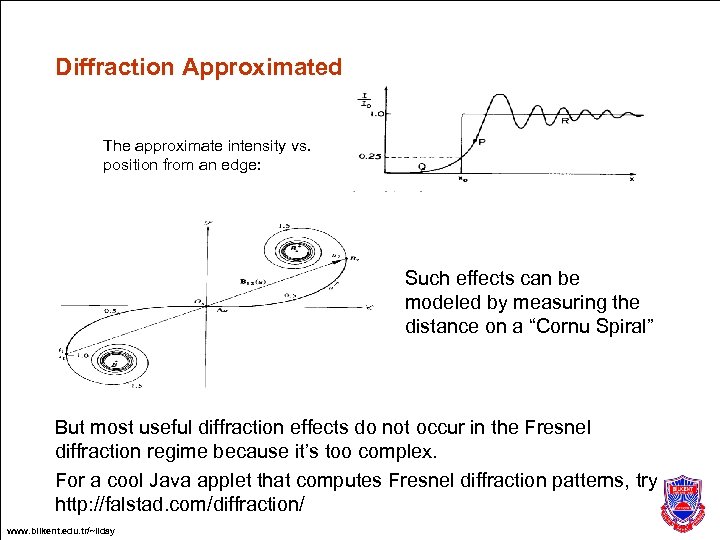Diffraction Approximated The approximate intensity vs. position from an edge: Such effects can be modeled by measuring the distance on a “Cornu Spiral” But most useful diffraction effects do not occur in the Fresnel diffraction regime because it’s too complex. For a cool Java applet that computes Fresnel diffraction patterns, try http: //falstad. com/diffraction/ www. bilkent. edu. tr/~ilday