63762d74fc639cbc3caa42d6e76ce4c6.ppt
- Количество слайдов: 154
 PHY 110, Introduction to Physics Dr. Henry SC 453, 572 -6164 (alt 572 -5309) E-Mail: henryh 1@nku. edu Web Site: www. nku. edu/~henryh 1/ © Hugh Henry, 2008
PHY 110, Introduction to Physics Dr. Henry SC 453, 572 -6164 (alt 572 -5309) E-Mail: henryh 1@nku. edu Web Site: www. nku. edu/~henryh 1/ © Hugh Henry, 2008
 If you are Tardy Initial beside Your Name on the Sheet on the Front Table
If you are Tardy Initial beside Your Name on the Sheet on the Front Table
 Chapter 5 Temperature and Heat
Chapter 5 Temperature and Heat
 Temperature n Temperature is loosely defined as a measure of the hotness or coldness of a substance. n Temperature is related to the average KE of the molecules in the substance. n Higher temperature reflects higher KE, and lower temperature reflects lower KE. The_Energy_of_Heat 4
Temperature n Temperature is loosely defined as a measure of the hotness or coldness of a substance. n Temperature is related to the average KE of the molecules in the substance. n Higher temperature reflects higher KE, and lower temperature reflects lower KE. The_Energy_of_Heat 4
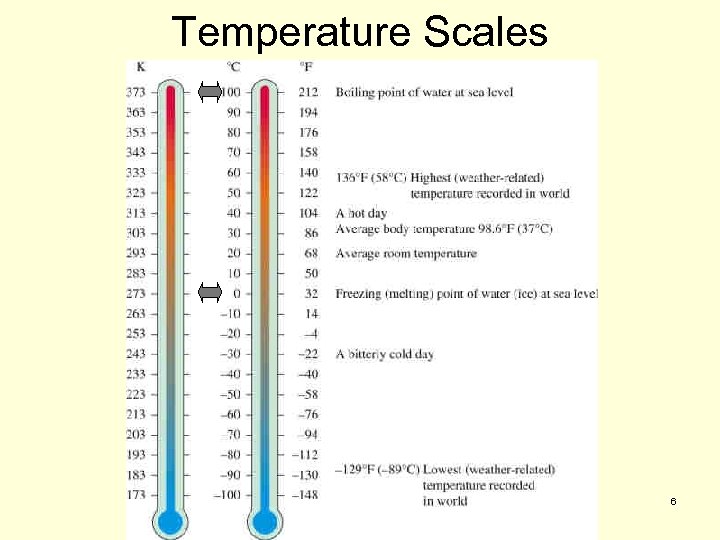
 Temperature n Temperature Scales have been developed to measure relative hotness and coldness. n We will review three such common scales: Kelvin n Celsius (or Centigrate) – most common worldwide. n Fahrenheit – most common in the US. n n The different temperature scales can be compared by examining the freezing and boiling points of water. 5
Temperature n Temperature Scales have been developed to measure relative hotness and coldness. n We will review three such common scales: Kelvin n Celsius (or Centigrate) – most common worldwide. n Fahrenheit – most common in the US. n n The different temperature scales can be compared by examining the freezing and boiling points of water. 5
 Temperature Scales 6
Temperature Scales 6
 Temperature, cont’d n Celsius (Centigrate) Scale n The freezing point of water is defined at 0°C. n The boiling point of water is defined at 100°C. n Fahrenheit Scale – used for US weather n 0°F is the freezing point of salt water. n 96°F is armpit temperature n Water freezes and boils at 32°F and 212°F. 7
Temperature, cont’d n Celsius (Centigrate) Scale n The freezing point of water is defined at 0°C. n The boiling point of water is defined at 100°C. n Fahrenheit Scale – used for US weather n 0°F is the freezing point of salt water. n 96°F is armpit temperature n Water freezes and boils at 32°F and 212°F. 7
 Temperature, cont’d n To convert from Celsius to Fahrenheit: n To convert from Fahrenheit to Celsius: 8
Temperature, cont’d n To convert from Celsius to Fahrenheit: n To convert from Fahrenheit to Celsius: 8
 Temperature, cont’d n Kelvin Scale n 0°K (called “absolute zero”) is the coldest possible temperature. n It is the temperature at which all random motion of matter is halted. n 0°C is 273. 159°K (usually approximated 273°) n Otherwise, the Kelvin scale follows the Celsius Scale n So, 0°K is -273. 159°C n On the Fahrenheit Scale, it is -459. 67°F. 9
Temperature, cont’d n Kelvin Scale n 0°K (called “absolute zero”) is the coldest possible temperature. n It is the temperature at which all random motion of matter is halted. n 0°C is 273. 159°K (usually approximated 273°) n Otherwise, the Kelvin scale follows the Celsius Scale n So, 0°K is -273. 159°C n On the Fahrenheit Scale, it is -459. 67°F. 9
![Temperature, cont’d n To convert from Celsius to Kelvin: [Ko] = [Co] + 273 Temperature, cont’d n To convert from Celsius to Kelvin: [Ko] = [Co] + 273](https://present5.com/presentation/63762d74fc639cbc3caa42d6e76ce4c6/image-10.jpg) Temperature, cont’d n To convert from Celsius to Kelvin: [Ko] = [Co] + 273 o 10
Temperature, cont’d n To convert from Celsius to Kelvin: [Ko] = [Co] + 273 o 10
 7
7
 Temperature, cont’d n For a definitive definition of temperature: n The Kelvin temperature of matter is proportional to the average kinetic energy of the constituent particles. n This helps explain many phenomena. n For example, it explains why the pressure of a gas increases as the temperature increases.
Temperature, cont’d n For a definitive definition of temperature: n The Kelvin temperature of matter is proportional to the average kinetic energy of the constituent particles. n This helps explain many phenomena. n For example, it explains why the pressure of a gas increases as the temperature increases.
 Temperature, cont’d n As the temperature of a gas increases, the average KE of the molecules increases – and hence their average speed. n Higher speed molecules colliding with the container walls impart more momentum and a larger force – hence increasing the pressure. 13
Temperature, cont’d n As the temperature of a gas increases, the average KE of the molecules increases – and hence their average speed. n Higher speed molecules colliding with the container walls impart more momentum and a larger force – hence increasing the pressure. 13
 Temperature and Pressure n Hence, if the volume of a gas is held constant (as in a container) when the temperature is increased, pressure and temperature are related through the expression: n This is the first rule in what physicists call the “ideal gas laws”: n With constant volume, the pressure of a gas is proportional to temperature. 14
Temperature and Pressure n Hence, if the volume of a gas is held constant (as in a container) when the temperature is increased, pressure and temperature are related through the expression: n This is the first rule in what physicists call the “ideal gas laws”: n With constant volume, the pressure of a gas is proportional to temperature. 14
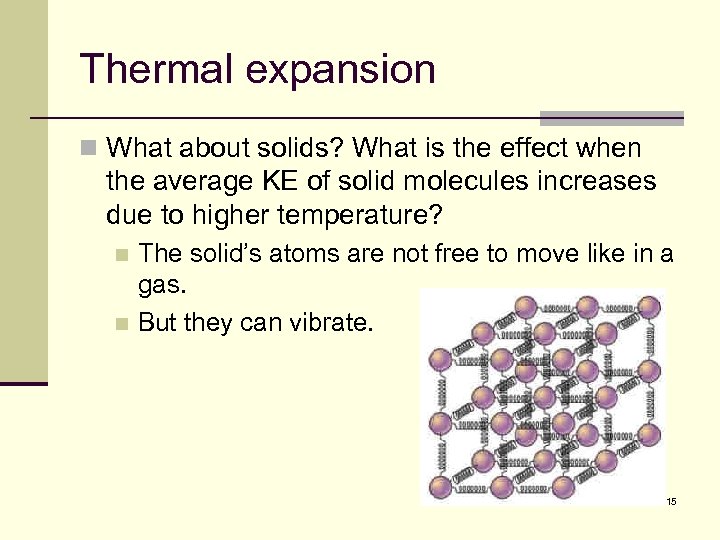 Thermal expansion n What about solids? What is the effect when the average KE of solid molecules increases due to higher temperature? The solid’s atoms are not free to move like in a gas. n But they can vibrate. n 15
Thermal expansion n What about solids? What is the effect when the average KE of solid molecules increases due to higher temperature? The solid’s atoms are not free to move like in a gas. n But they can vibrate. n 15
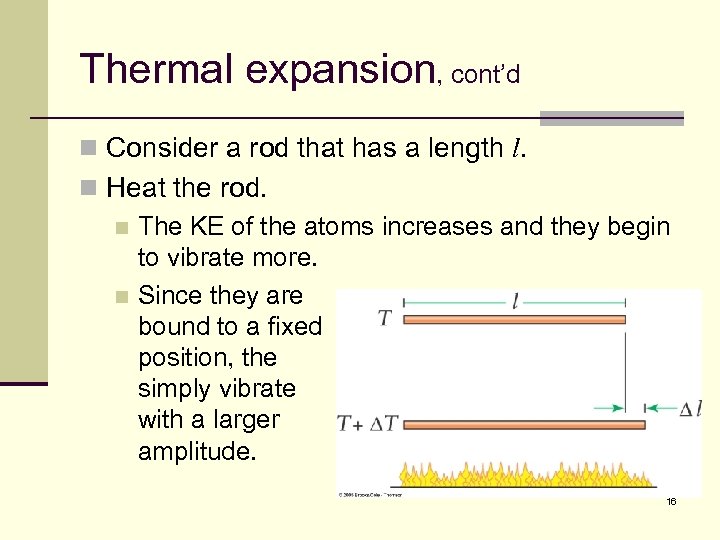 Thermal expansion, cont’d n Consider a rod that has a length l. n Heat the rod. n The KE of the atoms increases and they begin to vibrate more. n Since they are bound to a fixed position, the simply vibrate with a larger amplitude. 16
Thermal expansion, cont’d n Consider a rod that has a length l. n Heat the rod. n The KE of the atoms increases and they begin to vibrate more. n Since they are bound to a fixed position, the simply vibrate with a larger amplitude. 16
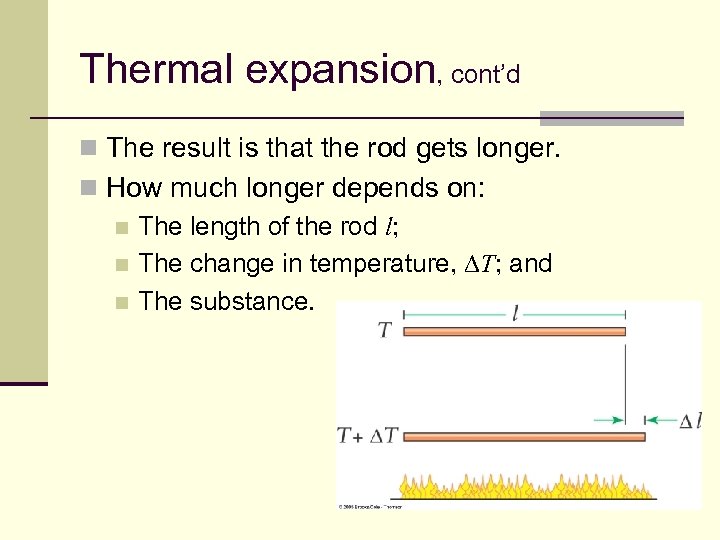 Thermal expansion, cont’d n The result is that the rod gets longer. n How much longer depends on: n The length of the rod l; n The change in temperature, DT; and n The substance. 17
Thermal expansion, cont’d n The result is that the rod gets longer. n How much longer depends on: n The length of the rod l; n The change in temperature, DT; and n The substance. 17
 Thermal expansion, cont’d n We can write this mathematically as Δl = αlΔT Dl is the change in the rod’s length, n a is the coefficient of linear expansion and has units of 1/°C, n l is the rod’s initial length (before the temperature change), and n DT is the change in temperature. n 18
Thermal expansion, cont’d n We can write this mathematically as Δl = αlΔT Dl is the change in the rod’s length, n a is the coefficient of linear expansion and has units of 1/°C, n l is the rod’s initial length (before the temperature change), and n DT is the change in temperature. n 18
 Thermal expansion, cont’d n Some materials expand more than others with the same increase in temperature n Coefficients of Linear Expansion have been identified for various materials Δl = αlΔT 19
Thermal expansion, cont’d n Some materials expand more than others with the same increase in temperature n Coefficients of Linear Expansion have been identified for various materials Δl = αlΔT 19
 Coefficients of Linear Expansion 20
Coefficients of Linear Expansion 20
 Example 5. 1 The Roebling Bridge is 494 meters long on a winter day when the temperature is -5°C. Assuming it is made of iron, how much longer is the span on a summer day when the temperature is 35°C? 21
Example 5. 1 The Roebling Bridge is 494 meters long on a winter day when the temperature is -5°C. Assuming it is made of iron, how much longer is the span on a summer day when the temperature is 35°C? 21
 Example 5. 1 ANSWER: The problem gives us: The change in temperature is: The change in length is 22
Example 5. 1 ANSWER: The problem gives us: The change in temperature is: The change in length is 22
 Example 5. 1 DISCUSSION: This is a change of over 9 inches – enough to buckle the bridge. Engineers compensate for this by providing expansion joints, as shown. 23
Example 5. 1 DISCUSSION: This is a change of over 9 inches – enough to buckle the bridge. Engineers compensate for this by providing expansion joints, as shown. 23
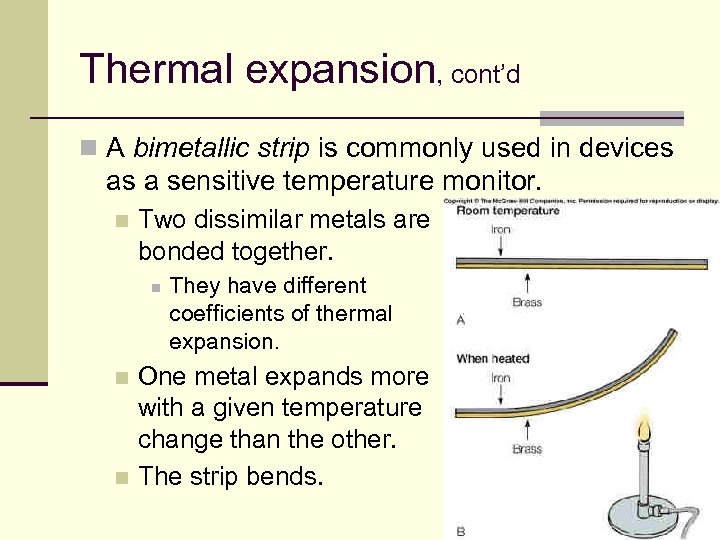 Thermal expansion, cont’d n A bimetallic strip is commonly used in devices as a sensitive temperature monitor. n Two dissimilar metals are bonded together. n They have different coefficients of thermal expansion. One metal expands more with a given temperature change than the other. n The strip bends. n 24
Thermal expansion, cont’d n A bimetallic strip is commonly used in devices as a sensitive temperature monitor. n Two dissimilar metals are bonded together. n They have different coefficients of thermal expansion. One metal expands more with a given temperature change than the other. n The strip bends. n 24
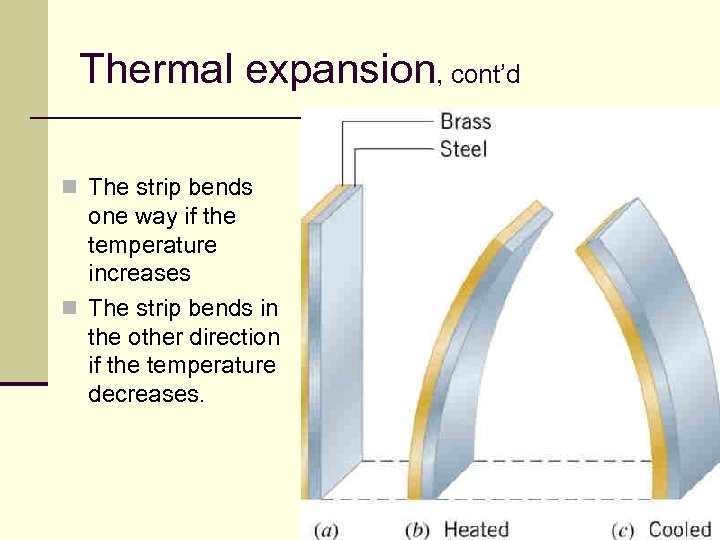 Thermal expansion, cont’d n The strip bends one way if the temperature increases n The strip bends in the other direction if the temperature decreases. 25
Thermal expansion, cont’d n The strip bends one way if the temperature increases n The strip bends in the other direction if the temperature decreases. 25
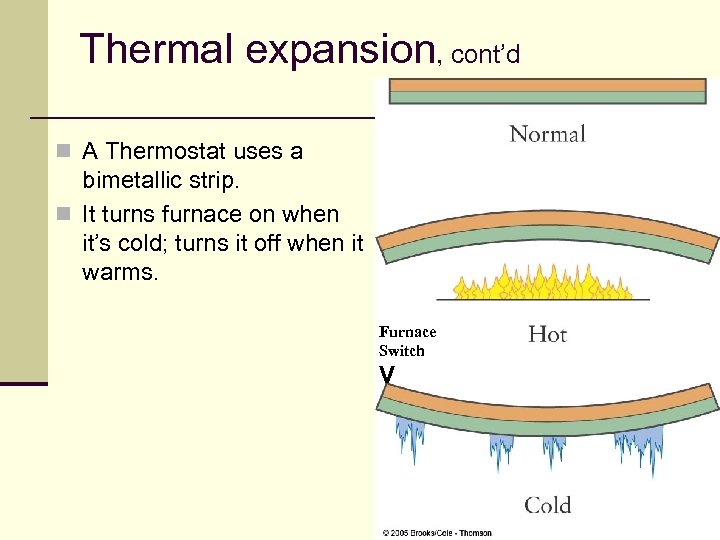 Thermal expansion, cont’d n A Thermostat uses a bimetallic strip. n It turns furnace on when it’s cold; turns it off when it warms. Furnace Switch V 26
Thermal expansion, cont’d n A Thermostat uses a bimetallic strip. n It turns furnace on when it’s cold; turns it off when it warms. Furnace Switch V 26
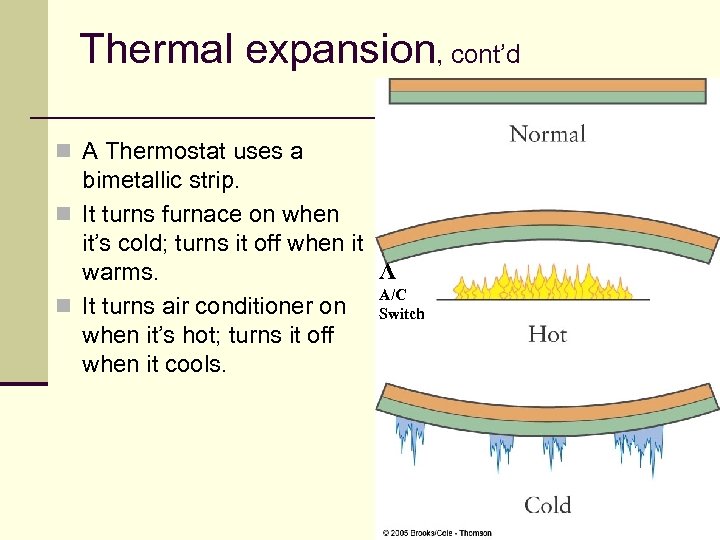 Thermal expansion, cont’d n A Thermostat uses a bimetallic strip. n It turns furnace on when it’s cold; turns it off when it Λ warms. A/C n It turns air conditioner on Switch when it’s hot; turns it off when it cools. 27
Thermal expansion, cont’d n A Thermostat uses a bimetallic strip. n It turns furnace on when it’s cold; turns it off when it Λ warms. A/C n It turns air conditioner on Switch when it’s hot; turns it off when it cools. 27
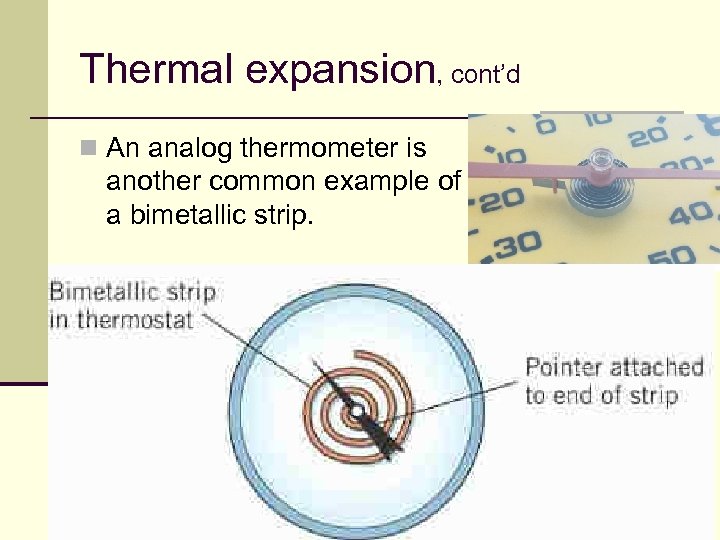 Thermal expansion, cont’d n An analog thermometer is another common example of a bimetallic strip. 28
Thermal expansion, cont’d n An analog thermometer is another common example of a bimetallic strip. 28
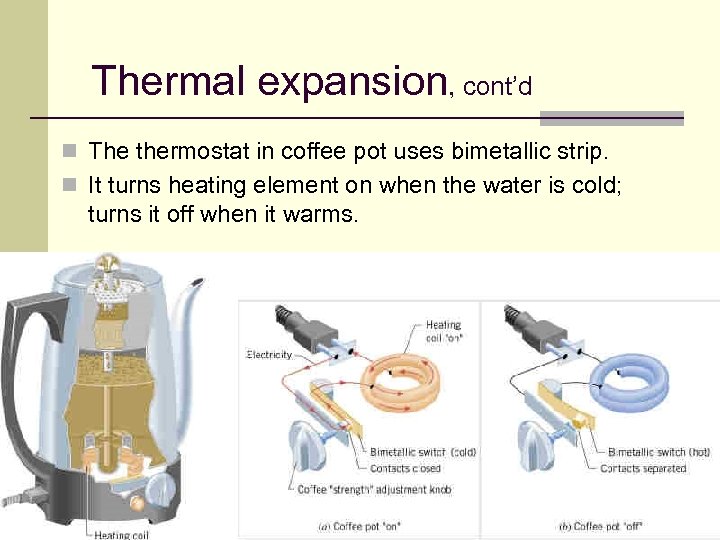 Thermal expansion, cont’d n The thermostat in coffee pot uses bimetallic strip. n It turns heating element on when the water is cold; turns it off when it warms. 29
Thermal expansion, cont’d n The thermostat in coffee pot uses bimetallic strip. n It turns heating element on when the water is cold; turns it off when it warms. 29
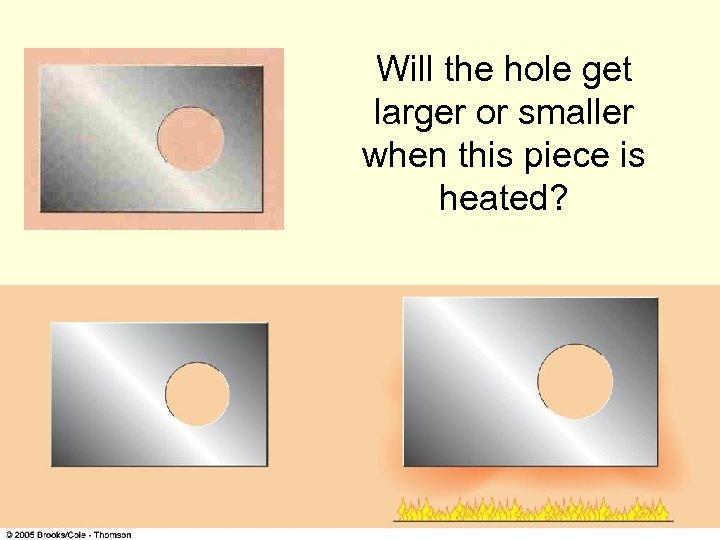 Will the hole get larger or smaller when this piece is heated?
Will the hole get larger or smaller when this piece is heated?
 Thermal expansion, Liquids n What about liquids? What is the effect when the average KE of liquid molecules increase due to higher temperature? n Liquid molecules can move about freely, but are always in contact with other atoms or molecules. 31
Thermal expansion, Liquids n What about liquids? What is the effect when the average KE of liquid molecules increase due to higher temperature? n Liquid molecules can move about freely, but are always in contact with other atoms or molecules. 31
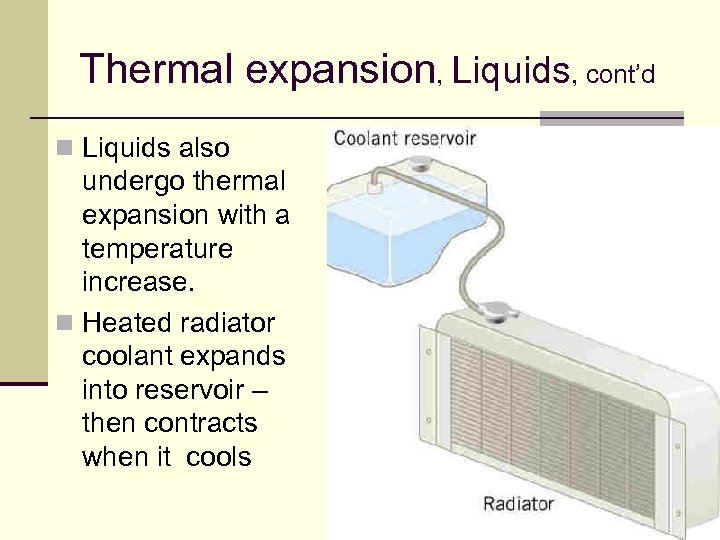 Thermal expansion, Liquids, cont’d n Liquids also undergo thermal expansion with a temperature increase. n Heated radiator coolant expands into reservoir – then contracts when it cools 32
Thermal expansion, Liquids, cont’d n Liquids also undergo thermal expansion with a temperature increase. n Heated radiator coolant expands into reservoir – then contracts when it cools 32
 Thermal expansion, Water n Water is a special case. n A volume of water increases with an increase in temperature above 4°C. n But between 0° and 4°C, water contracts with an increase in temperature. 33
Thermal expansion, Water n Water is a special case. n A volume of water increases with an increase in temperature above 4°C. n But between 0° and 4°C, water contracts with an increase in temperature. 33
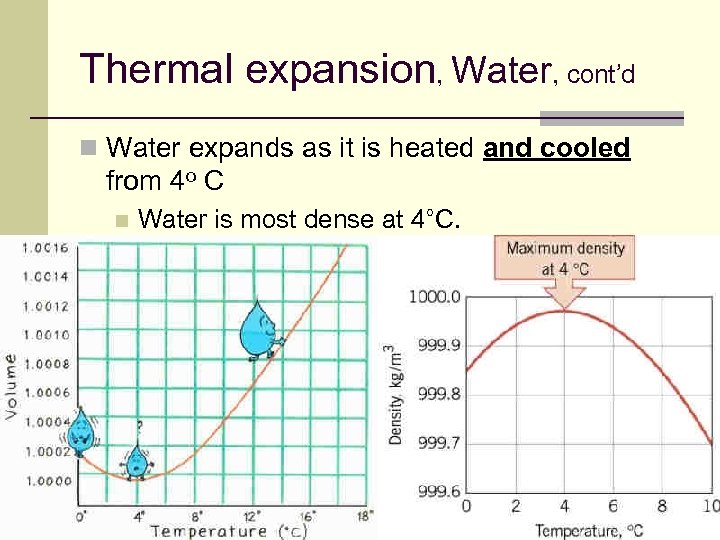 Thermal expansion, Water, cont’d n Water expands as it is heated and cooled from 4 o C n Water is most dense at 4°C. 34
Thermal expansion, Water, cont’d n Water expands as it is heated and cooled from 4 o C n Water is most dense at 4°C. 34
 Thermal expansion, Water, cont’d Ice is less dense than water n Iceberg at 0 o surrounded by water above 0 o n Iceberg floats because its density is lower than the surrounding water; it displaces its weight in water (Archimedes’ Principle) n Since density of ice is very close to density of water, most of iceberg is below the surface 35
Thermal expansion, Water, cont’d Ice is less dense than water n Iceberg at 0 o surrounded by water above 0 o n Iceberg floats because its density is lower than the surrounding water; it displaces its weight in water (Archimedes’ Principle) n Since density of ice is very close to density of water, most of iceberg is below the surface 35
 Thermal expansion, Gas n We have learned that increasing the temperature of gas molecules with a constant volume causes an increase in pressure. n What happens when the volume is not constant – like in a balloon? 36
Thermal expansion, Gas n We have learned that increasing the temperature of gas molecules with a constant volume causes an increase in pressure. n What happens when the volume is not constant – like in a balloon? 36
 Thermal expansion, Gas, cont’d n If gas volume is not kept to constant, gases also expand with an increase in temperature. n For an expanding container which keeps gas at pressure constant, the volume of a gas is proportional to its temperature: VαT n A balloon, for example, has (almost) constant pressure since the balloon is capable of expanding. n This means that if you heat a balloon, the volume will increase. 37
Thermal expansion, Gas, cont’d n If gas volume is not kept to constant, gases also expand with an increase in temperature. n For an expanding container which keeps gas at pressure constant, the volume of a gas is proportional to its temperature: VαT n A balloon, for example, has (almost) constant pressure since the balloon is capable of expanding. n This means that if you heat a balloon, the volume will increase. 37
 Thermal Expansion, T = 273 K Gas, cont’d n A 10% increase in temperature (with constant pressure) will cause a 10% increase in volume T = 300 K VαT n NOTE: Temperature for this proportionality must be in Kelvin 38
Thermal Expansion, T = 273 K Gas, cont’d n A 10% increase in temperature (with constant pressure) will cause a 10% increase in volume T = 300 K VαT n NOTE: Temperature for this proportionality must be in Kelvin 38
 Hot Air Balloon Based on Thermal Expansion of Gas 39
Hot Air Balloon Based on Thermal Expansion of Gas 39
 Thermal expansion, cont’d n What if we let the pressure, volume and temperature change? n These three quantities are related through the ideal gas law: p. V α T n This is the general statement from which the previous examples are special cases. 40
Thermal expansion, cont’d n What if we let the pressure, volume and temperature change? n These three quantities are related through the ideal gas law: p. V α T n This is the general statement from which the previous examples are special cases. 40
 The Laws of Thermodynamics The_Three_Laws_of_Thermodynamics
The Laws of Thermodynamics The_Three_Laws_of_Thermodynamics
 First law of thermodynamics Conservation of Energy: Energy is neither created nor destroyed, merely changed in form. n The First Law of Thermodynamics applies Conservation of Energy to Internal Energy and Heat. n We will now expand our definition of Internal Energy (introduced in chapter 3) and Heat. 42
First law of thermodynamics Conservation of Energy: Energy is neither created nor destroyed, merely changed in form. n The First Law of Thermodynamics applies Conservation of Energy to Internal Energy and Heat. n We will now expand our definition of Internal Energy (introduced in chapter 3) and Heat. 42
 First law of thermodynamics, cont’d n The Internal energy of an object was introduced as energy associated with the internal structure of the object. n We have now learned that the temperature of an object is proportional to the average kinetic energy of the constituent particles of a substance. 43
First law of thermodynamics, cont’d n The Internal energy of an object was introduced as energy associated with the internal structure of the object. n We have now learned that the temperature of an object is proportional to the average kinetic energy of the constituent particles of a substance. 43
 First law of thermodynamics, cont’d n So now we define Internal energy (U) as the sum of the kinetic and potential energies of all the atoms and molecules in a substance. Internal energy is represented by the symbol U. n For gases, we only deal with the kinetic energy part of the internal energy. n n n The particles interact only during collisions. Potential Energy plays a role only with solids and liquids. 44
First law of thermodynamics, cont’d n So now we define Internal energy (U) as the sum of the kinetic and potential energies of all the atoms and molecules in a substance. Internal energy is represented by the symbol U. n For gases, we only deal with the kinetic energy part of the internal energy. n n n The particles interact only during collisions. Potential Energy plays a role only with solids and liquids. 44
 First law of thermodynamics, cont’d n We define Heat (Q) as a form of energy that is transferred between two substances because they have different temperatures. An object does not have heat. n An object transfers heat when its temperature is raised by contact with a hotter object or lowered by contact with a cooler object. n Heat is represented by the symbol Q. n n Increasing (or decreasing) temperature by adding (or removing) heat increases (or decreases) an object’s Kinetic Energy, and hence its Internal Energy. 45
First law of thermodynamics, cont’d n We define Heat (Q) as a form of energy that is transferred between two substances because they have different temperatures. An object does not have heat. n An object transfers heat when its temperature is raised by contact with a hotter object or lowered by contact with a cooler object. n Heat is represented by the symbol Q. n n Increasing (or decreasing) temperature by adding (or removing) heat increases (or decreases) an object’s Kinetic Energy, and hence its Internal Energy. 45
 Aristotle. . . Wrong Again n Aristotle believed heat is a quantity. n Remember. . . Greek science used thought – not experiments – to develop physical laws. n This attitude persisted up through the 19 th century when the Laws of Thermodynamics were developed by experimentation. Aristotle (384 -322 BC)
Aristotle. . . Wrong Again n Aristotle believed heat is a quantity. n Remember. . . Greek science used thought – not experiments – to develop physical laws. n This attitude persisted up through the 19 th century when the Laws of Thermodynamics were developed by experimentation. Aristotle (384 -322 BC)
 First law of thermodynamics, cont’d n Heat is a transfer of energy. n Joules is the SI unit for energy n Hence Joules is a unit for heat. n An alternate unit of energy/heat is the calorie 1 cal = 4. 184 J
First law of thermodynamics, cont’d n Heat is a transfer of energy. n Joules is the SI unit for energy n Hence Joules is a unit for heat. n An alternate unit of energy/heat is the calorie 1 cal = 4. 184 J
 46
46
 First law of thermodynamics, cont’d To understand The First Law of Thermodynamics, consider how we can increase the temperature of an object. . . ie, increase the internal energy of the object. 49
First law of thermodynamics, cont’d To understand The First Law of Thermodynamics, consider how we can increase the temperature of an object. . . ie, increase the internal energy of the object. 49
 First law of thermodynamics, cont’d n One way to increase an object’s temperature is to do work on it. n Consider pushing on a piston to do work on a gas in a cylinder. Applying a force to push the piston down a distance means work is done: work = Fd. n This work transfers energy to the gas n 50
First law of thermodynamics, cont’d n One way to increase an object’s temperature is to do work on it. n Consider pushing on a piston to do work on a gas in a cylinder. Applying a force to push the piston down a distance means work is done: work = Fd. n This work transfers energy to the gas n 50
 First law of thermodynamics, cont’d n Pushing on a piston to compress a gas in a cylinder also forces the molecules closer together, increasing the pressure. n Higher gas pressure plus energy transfer imply greater KE of the gas molecules. n Hence the temperature of a gas increases when it is compressed. n It gets hot. 51
First law of thermodynamics, cont’d n Pushing on a piston to compress a gas in a cylinder also forces the molecules closer together, increasing the pressure. n Higher gas pressure plus energy transfer imply greater KE of the gas molecules. n Hence the temperature of a gas increases when it is compressed. n It gets hot. 51
 First law of thermodynamics, cont’d n A diesel engine uses this concept. n The diesel/air mixture is compressed in the cylinder. n At maximum compression the mixture ignites. n The pressure increase from the explosion pushes the piston down. n This causes the crankshaft to turn. n Compression of air to 1/20 th of its volume raises the temperature from 27 o. C to 721 o. C 52
First law of thermodynamics, cont’d n A diesel engine uses this concept. n The diesel/air mixture is compressed in the cylinder. n At maximum compression the mixture ignites. n The pressure increase from the explosion pushes the piston down. n This causes the crankshaft to turn. n Compression of air to 1/20 th of its volume raises the temperature from 27 o. C to 721 o. C 52
 First law of thermodynamics, cont’d Work can be positive or negative. n When a gas is compressed, positive work is done on the gas. n The temperature increases. n When a gas expands, negative work is done on the gas. n The temperature decreases. 53
First law of thermodynamics, cont’d Work can be positive or negative. n When a gas is compressed, positive work is done on the gas. n The temperature increases. n When a gas expands, negative work is done on the gas. n The temperature decreases. 53
 First law of thermodynamics, cont’d n Compressing a gas increases its temperature, and allowing a gas to expand decreases its temperature. n Temperature is related to the average kinetic energy of the gas atoms/molecules. n Hence, compressing (or expanding) a gas increases (or decreases) its internal energy. 54
First law of thermodynamics, cont’d n Compressing a gas increases its temperature, and allowing a gas to expand decreases its temperature. n Temperature is related to the average kinetic energy of the gas atoms/molecules. n Hence, compressing (or expanding) a gas increases (or decreases) its internal energy. 54
 First law of thermodynamics, cont’d n Another way to increase an object’s temperature is to expose it to something with a higher temperature. n In this way we transfer heat into the object. 55
First law of thermodynamics, cont’d n Another way to increase an object’s temperature is to expose it to something with a higher temperature. n In this way we transfer heat into the object. 55
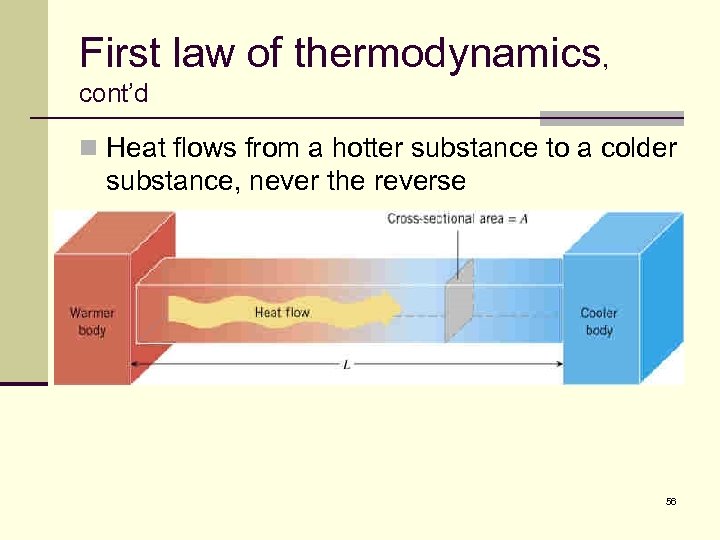 First law of thermodynamics, cont’d n Heat flows from a hotter substance to a colder substance, never the reverse 56
First law of thermodynamics, cont’d n Heat flows from a hotter substance to a colder substance, never the reverse 56
 First law of thermodynamics, cont’d n The First Law of Thermodynamics states that the change in internal energy of a substance equals the work done on it plus the heat transferred to it: ΔU = work + Q n The First Law of Thermodynamics is Conservation of Energy applied to Heat: Energy is neither created nor destroyed, merely changed in form. 57
First law of thermodynamics, cont’d n The First Law of Thermodynamics states that the change in internal energy of a substance equals the work done on it plus the heat transferred to it: ΔU = work + Q n The First Law of Thermodynamics is Conservation of Energy applied to Heat: Energy is neither created nor destroyed, merely changed in form. 57
 First law of thermodynamics, cont’d n When a gas is compressed and positive work is done on the gas. n The change in internal energy is positive: the internal energy of the gas increases. n When a gas expands and negative work is done on the gas. n ΔU = work + Q The change in internal energy is negative: the internal energy of the gas decreases. 58
First law of thermodynamics, cont’d n When a gas is compressed and positive work is done on the gas. n The change in internal energy is positive: the internal energy of the gas increases. n When a gas expands and negative work is done on the gas. n ΔU = work + Q The change in internal energy is negative: the internal energy of the gas decreases. 58
 First law of thermodynamics, cont’d n When heat flows into a substance, its internal energy increases n When heat flows out of a substance, its internal energy decreases ΔU = work + Q 59
First law of thermodynamics, cont’d n When heat flows into a substance, its internal energy increases n When heat flows out of a substance, its internal energy decreases ΔU = work + Q 59
 Heat Transfer n There are three ways to increase the internal energy of a substance by transferring heat into it: Conduction: the transfer of heat between atoms and molecules in direct contact. n Convection: the transfer of heat by buoyant mixing in a fluid. n Radiation: the transfer of heat by way of electromagnetic waves. n 60
Heat Transfer n There are three ways to increase the internal energy of a substance by transferring heat into it: Conduction: the transfer of heat between atoms and molecules in direct contact. n Convection: the transfer of heat by buoyant mixing in a fluid. n Radiation: the transfer of heat by way of electromagnetic waves. n 60
 Heat transfer — conduction n Heat is conducted across the boundary between two substances. For a pan on a stove, the conduction occurs because the flame is in contact with the bottom of the pan. n Conduction also occurs within the pan. n n Contact with the hot bottom makes the sides hot – then the handle. 61
Heat transfer — conduction n Heat is conducted across the boundary between two substances. For a pan on a stove, the conduction occurs because the flame is in contact with the bottom of the pan. n Conduction also occurs within the pan. n n Contact with the hot bottom makes the sides hot – then the handle. 61
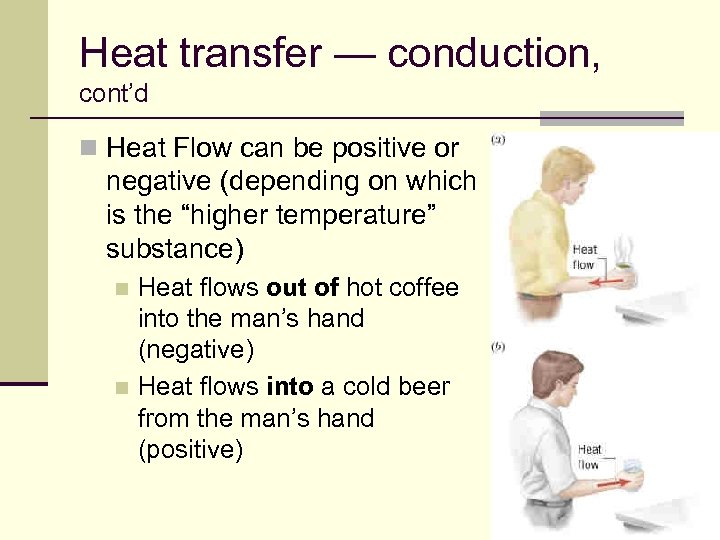 Heat transfer — conduction, cont’d n Heat Flow can be positive or negative (depending on which is the “higher temperature” substance) Heat flows out of hot coffee into the man’s hand (negative) n Heat flows into a cold beer from the man’s hand (positive) n 62
Heat transfer — conduction, cont’d n Heat Flow can be positive or negative (depending on which is the “higher temperature” substance) Heat flows out of hot coffee into the man’s hand (negative) n Heat flows into a cold beer from the man’s hand (positive) n 62
 Heat transfer — conduction, cont’d n Thermal insulators are materials through which energy is transferred slowly. n Wool is a good thermal insulator because it contains large amounts of trapped air that slow down the transfer of energy. n Thermal conductors are materials through which energy is transferred quickly. n Metals are good thermal conductors because they contain electrons that are free to move throughout the material. 63
Heat transfer — conduction, cont’d n Thermal insulators are materials through which energy is transferred slowly. n Wool is a good thermal insulator because it contains large amounts of trapped air that slow down the transfer of energy. n Thermal conductors are materials through which energy is transferred quickly. n Metals are good thermal conductors because they contain electrons that are free to move throughout the material. 63
 Heat transfer — conduction, cont’d n A hard-wood floor feels colder than a carpeted floor because the wood conducts heat more quickly from your foot than the carpet. n You can judge a good conductor if it feels colder than another substance at the same temperature. 64
Heat transfer — conduction, cont’d n A hard-wood floor feels colder than a carpeted floor because the wood conducts heat more quickly from your foot than the carpet. n You can judge a good conductor if it feels colder than another substance at the same temperature. 64
 Heat transfer — conduction, cont’d n We put insulation on our homes to minimize the flow of heat outside by conduction 65
Heat transfer — conduction, cont’d n We put insulation on our homes to minimize the flow of heat outside by conduction 65
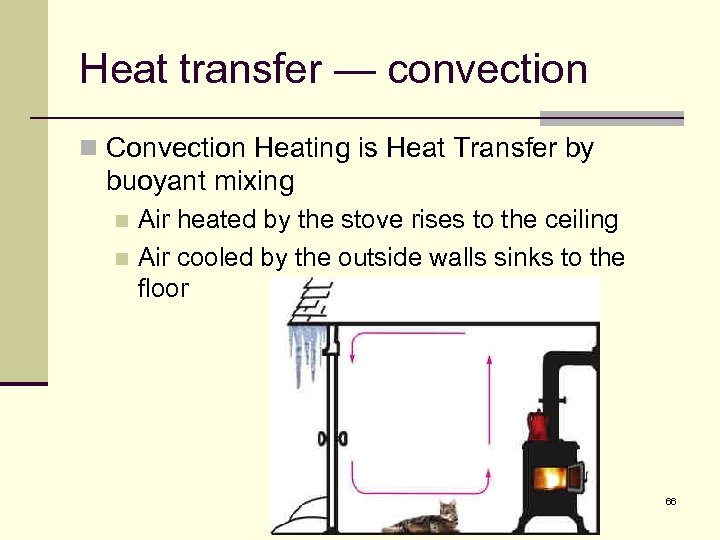 Heat transfer — convection n Convection Heating is Heat Transfer by buoyant mixing Air heated by the stove rises to the ceiling n Air cooled by the outside walls sinks to the floor n 66
Heat transfer — convection n Convection Heating is Heat Transfer by buoyant mixing Air heated by the stove rises to the ceiling n Air cooled by the outside walls sinks to the floor n 66
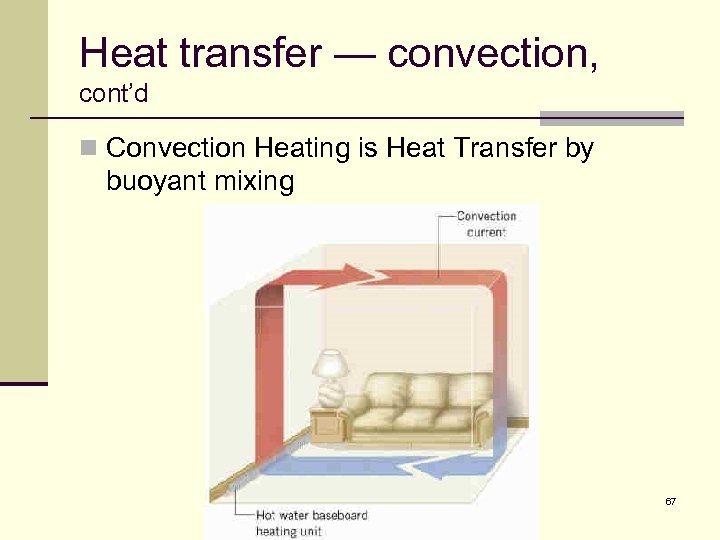 Heat transfer — convection, cont’d n Convection Heating is Heat Transfer by buoyant mixing 67
Heat transfer — convection, cont’d n Convection Heating is Heat Transfer by buoyant mixing 67
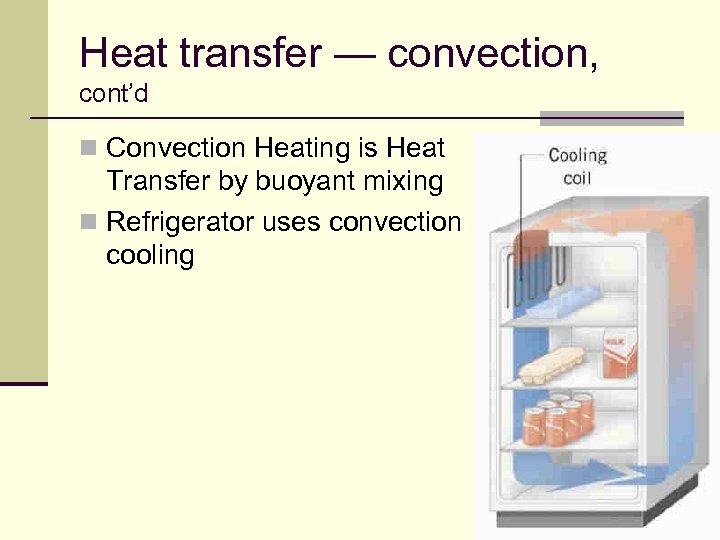 Heat transfer — convection, cont’d n Convection Heating is Heat Transfer by buoyant mixing n Refrigerator uses convection cooling 68
Heat transfer — convection, cont’d n Convection Heating is Heat Transfer by buoyant mixing n Refrigerator uses convection cooling 68
 Heat transfer — convection, cont’d n Convection Heating is Heat Transfer by buoyant mixing n Pot of boiling water on a stove is an example of conduction and convection 69
Heat transfer — convection, cont’d n Convection Heating is Heat Transfer by buoyant mixing n Pot of boiling water on a stove is an example of conduction and convection 69
 Heat transfer — convection, cont’d n Convective cooling by the wind can ameliorate temperatures. For example: n During the day, the ground warms more quickly than the water. n n The warm air rises, and cooler air moves-in from the sea to replace it. During the night, the water retains its heat longer than the ground. n Warmer sea air rises, and cooler air on the ground moves to replace it. n This reflects water’s high Specific Heat Capacity – our next topic. 70
Heat transfer — convection, cont’d n Convective cooling by the wind can ameliorate temperatures. For example: n During the day, the ground warms more quickly than the water. n n The warm air rises, and cooler air moves-in from the sea to replace it. During the night, the water retains its heat longer than the ground. n Warmer sea air rises, and cooler air on the ground moves to replace it. n This reflects water’s high Specific Heat Capacity – our next topic. 70
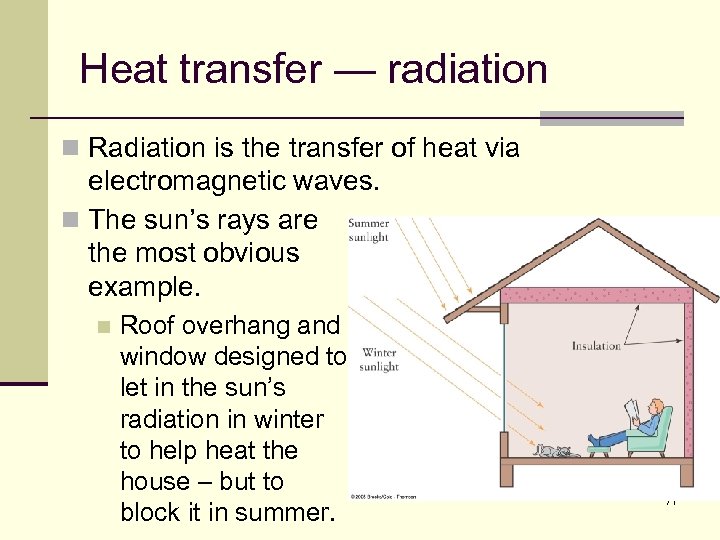 Heat transfer — radiation n Radiation is the transfer of heat via electromagnetic waves. n The sun’s rays are the most obvious example. n Roof overhang and window designed to let in the sun’s radiation in winter to help heat the house – but to block it in summer. 71
Heat transfer — radiation n Radiation is the transfer of heat via electromagnetic waves. n The sun’s rays are the most obvious example. n Roof overhang and window designed to let in the sun’s radiation in winter to help heat the house – but to block it in summer. 71
 Heat transfer — radiation n Radiation is the transfer of heat via electromagnetic waves. n A light bulb represents all 3 methods of heat transfer: n n n The bulb warms the air through conduction. The warm air rises through convection. The bulb radiates visible light and some as infra-red radiation – which are both electromagnetic waves. 72
Heat transfer — radiation n Radiation is the transfer of heat via electromagnetic waves. n A light bulb represents all 3 methods of heat transfer: n n n The bulb warms the air through conduction. The warm air rises through convection. The bulb radiates visible light and some as infra-red radiation – which are both electromagnetic waves. 72
 Heat transfer — radiation, cont’d n Radiation is the transfer of heat via electromagnetic waves. n Earth receives a large input of heat from the Sun’s radiation n Solar Activity is the Primary Contributor to the Earth’s Temperature n More on the Earth’s Temperature later. . . 73
Heat transfer — radiation, cont’d n Radiation is the transfer of heat via electromagnetic waves. n Earth receives a large input of heat from the Sun’s radiation n Solar Activity is the Primary Contributor to the Earth’s Temperature n More on the Earth’s Temperature later. . . 73
 The First Law of Thermodynamics ΔU = work + Q You Can’t Get Somethin’ for Nothin’
The First Law of Thermodynamics ΔU = work + Q You Can’t Get Somethin’ for Nothin’
 Specific heat capacity n Transferring heat to/from a substance changes its internal energy. n The substance’s change in temperature for a given change in internal energy – ie, for a given increase (or loss) of heat – depends on the characteristics of the substance. 75
Specific heat capacity n Transferring heat to/from a substance changes its internal energy. n The substance’s change in temperature for a given change in internal energy – ie, for a given increase (or loss) of heat – depends on the characteristics of the substance. 75
 Specific heat capacity, cont’d n The amount of heat transferred is proportional to the change in temperature: n It takes more heat to raise the temperature a lot than a little Q α ΔT n The amount of heat necessary to effect a certain temperature change depends on the mass of the substance: Qαm n More mass means more particles absorb the added energy. 76
Specific heat capacity, cont’d n The amount of heat transferred is proportional to the change in temperature: n It takes more heat to raise the temperature a lot than a little Q α ΔT n The amount of heat necessary to effect a certain temperature change depends on the mass of the substance: Qαm n More mass means more particles absorb the added energy. 76
 Specific heat capacity, cont’d n The amount of heat transferred to accomplish a certain temperature depends on the type of material. n We characterize materials by their specific heat capacity, C: n The amount of energy required to raise the temperature of 1 kg of a substance by 1°C n We write n QαC The higher the specific heat capacity, the more heat is needed to raise temperature 1°C 77
Specific heat capacity, cont’d n The amount of heat transferred to accomplish a certain temperature depends on the type of material. n We characterize materials by their specific heat capacity, C: n The amount of energy required to raise the temperature of 1 kg of a substance by 1°C n We write n QαC The higher the specific heat capacity, the more heat is needed to raise temperature 1°C 77
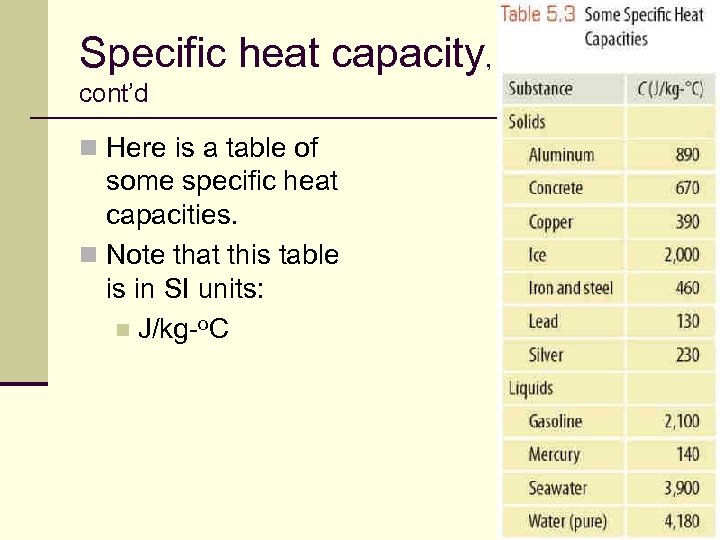 Specific heat capacity, cont’d n Here is a table of some specific heat capacities. n Note that this table is in SI units: n J/kg-o. C 78
Specific heat capacity, cont’d n Here is a table of some specific heat capacities. n Note that this table is in SI units: n J/kg-o. C 78
 Specific heat capacity, cont’d n The higher Specific Heat Capacity of water vs iron reflects the fact that more heat is required to raise the temperature of water by 1 o than the temperature of iron by 1 o 79
Specific heat capacity, cont’d n The higher Specific Heat Capacity of water vs iron reflects the fact that more heat is required to raise the temperature of water by 1 o than the temperature of iron by 1 o 79
 Specific heat capacity, cont’d n All these relationships are expressed by the formula: Q = m. CΔT 80
Specific heat capacity, cont’d n All these relationships are expressed by the formula: Q = m. CΔT 80
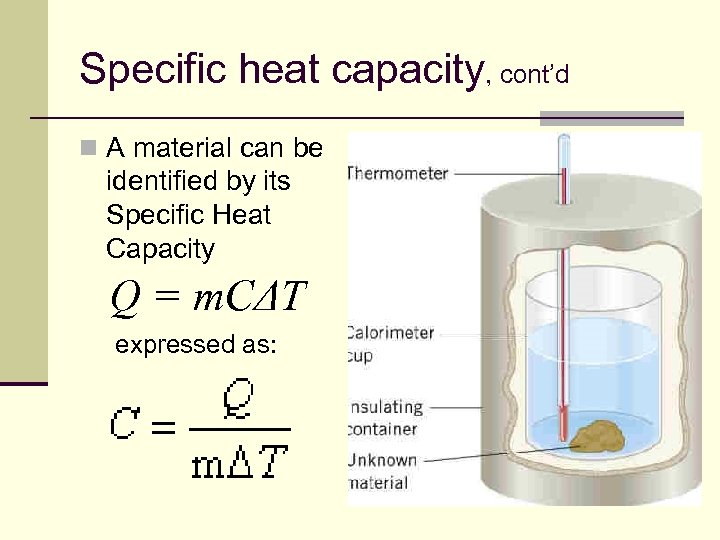 Specific heat capacity, cont’d n A material can be identified by its Specific Heat Capacity Q = m. CΔT expressed as: 81
Specific heat capacity, cont’d n A material can be identified by its Specific Heat Capacity Q = m. CΔT expressed as: 81
 Example 5. 2 Let’s compute how much energy it takes to make a cup of coffee or tea. Eight ounces of water has a mass of about 0. 22 kilograms. How much heat must be transferred to the water to raise its temperature from 20°C to the boiling point, 100°C? 82
Example 5. 2 Let’s compute how much energy it takes to make a cup of coffee or tea. Eight ounces of water has a mass of about 0. 22 kilograms. How much heat must be transferred to the water to raise its temperature from 20°C to the boiling point, 100°C? 82
 Example 5. 2 ANSWER: The problem gives us: The temperature change is The heat transferred is 83
Example 5. 2 ANSWER: The problem gives us: The temperature change is The heat transferred is 83
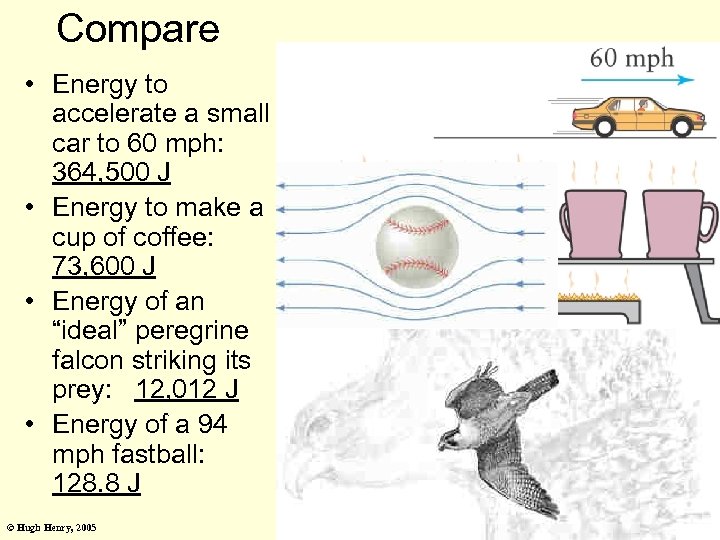 Compare • Energy to accelerate a small car to 60 mph: 364, 500 J • Energy to make a cup of coffee: 73, 600 J • Energy of an “ideal” peregrine falcon striking its prey: 12, 012 J • Energy of a 94 mph fastball: 128. 8 J © Hugh Henry, 2005 84
Compare • Energy to accelerate a small car to 60 mph: 364, 500 J • Energy to make a cup of coffee: 73, 600 J • Energy of an “ideal” peregrine falcon striking its prey: 12, 012 J • Energy of a 94 mph fastball: 128. 8 J © Hugh Henry, 2005 84
 Example 5. 3 A 5 -kilogram concrete block falls to the ground from a height of 10 meters. If all of its original potential energy goes to heat the block when it hits the ground, what is its change in temperature? 85
Example 5. 3 A 5 -kilogram concrete block falls to the ground from a height of 10 meters. If all of its original potential energy goes to heat the block when it hits the ground, what is its change in temperature? 85
 Example 5. 3 ANSWER: The problem gives us: The potential energy of the block is: 86
Example 5. 3 ANSWER: The problem gives us: The potential energy of the block is: 86
 Example 5. 3 ANSWER: This energy equals the heat transferred to the block: The temperature change is found from 87
Example 5. 3 ANSWER: This energy equals the heat transferred to the block: The temperature change is found from 87
 Example 5. 3 ANSWER: The resulting temperature change is 88
Example 5. 3 ANSWER: The resulting temperature change is 88
 Example 5. 2 DISCUSSION: We typically do notice the temperature changes associated with everyday actions. They are usually too small to be noticed. But not always… 89
Example 5. 2 DISCUSSION: We typically do notice the temperature changes associated with everyday actions. They are usually too small to be noticed. But not always… 89
 Example 5. 4 In chapter 2 we calculated that a satellite in low Earth orbit has a velocity ~7, 900 m/s. Assume this satellite experiences air resistance and re-enters the Earth’s atmosphere. As it moves downward through increasingly dense air, the friction force of air resistance converts the satellite’s kinetic energy into internal energy. If the satellite is mostly aluminum and all of its kinetic energy is converted into internal energy, what would be its temperature increase? 90
Example 5. 4 In chapter 2 we calculated that a satellite in low Earth orbit has a velocity ~7, 900 m/s. Assume this satellite experiences air resistance and re-enters the Earth’s atmosphere. As it moves downward through increasingly dense air, the friction force of air resistance converts the satellite’s kinetic energy into internal energy. If the satellite is mostly aluminum and all of its kinetic energy is converted into internal energy, what would be its temperature increase? 90
 Example 5. 4 ANSWER: The problem gives us: The kinetic energy of the satellite is: The heat transferred to the satellite is: Q = m. CΔT 91
Example 5. 4 ANSWER: The problem gives us: The kinetic energy of the satellite is: The heat transferred to the satellite is: Q = m. CΔT 91
 Example 5. 4 ANSWER: These two energies are equal since all of its KE is transformed into heat: The temperature change is 92
Example 5. 4 ANSWER: These two energies are equal since all of its KE is transformed into heat: The temperature change is 92
 Example 5. 4 DISCUSSION: In this idealized example, we did not consider the satellite’s potential energy, because the it is assumed to be in orbit at the earth’s surface. A more complete calculation must consider PE. This idealized example also fails to account for the fact that the atmosphere would serve as a cooling medium during re-entry. 93
Example 5. 4 DISCUSSION: In this idealized example, we did not consider the satellite’s potential energy, because the it is assumed to be in orbit at the earth’s surface. A more complete calculation must consider PE. This idealized example also fails to account for the fact that the atmosphere would serve as a cooling medium during re-entry. 93
 Example 5. 4 DISCUSSION: Nevertheless, this makes the point that a satellite re-entering the atmosphere generates a lot of heat. Even if 90% of the energy was lost in cooling by the atmosphere, the remaining 10% would be enough to vaporize almost all of the satellite. This is why most space debris entering our atmosphere doesn’t reach the surface of earth. 94
Example 5. 4 DISCUSSION: Nevertheless, this makes the point that a satellite re-entering the atmosphere generates a lot of heat. Even if 90% of the energy was lost in cooling by the atmosphere, the remaining 10% would be enough to vaporize almost all of the satellite. This is why most space debris entering our atmosphere doesn’t reach the surface of earth. 94
 The high heat generated when an object falls through the atmosphere is illustrated by this police dashboard camera movieearthmeteor movie of a meteor hitting the of a near falling near Edmonton, Alberta, Canada (police dashboard camera) Meteor
The high heat generated when an object falls through the atmosphere is illustrated by this police dashboard camera movieearthmeteor movie of a meteor hitting the of a near falling near Edmonton, Alberta, Canada (police dashboard camera) Meteor
 Space Shuttle Columbia Disaster n “Streaking through the atmosphere at 18 times the speed of sound, Columbia disintegrated Saturday morning [Feb 1, 2003]. ” – CNN n The reason was that ceramic insulating tiles, installed to absorb re-entry heat and insulate it from the aluminum skin of the space shuttle. 96
Space Shuttle Columbia Disaster n “Streaking through the atmosphere at 18 times the speed of sound, Columbia disintegrated Saturday morning [Feb 1, 2003]. ” – CNN n The reason was that ceramic insulating tiles, installed to absorb re-entry heat and insulate it from the aluminum skin of the space shuttle. 96
 Space Shuttle Columbia Disaster As a possible extra credit project. . . n Calculate the maximum possible temperature rise of the Space Shuttle as it enters the atmosphere. n Assume the Space Shuttle weighs 75, 000 kg, its average orbit is 400 km high, and it travels at a speed of about 7, 500 m/s n Use Q = CmΔT = KE + PE = ½ mv 2 + mgh 97
Space Shuttle Columbia Disaster As a possible extra credit project. . . n Calculate the maximum possible temperature rise of the Space Shuttle as it enters the atmosphere. n Assume the Space Shuttle weighs 75, 000 kg, its average orbit is 400 km high, and it travels at a speed of about 7, 500 m/s n Use Q = CmΔT = KE + PE = ½ mv 2 + mgh 97
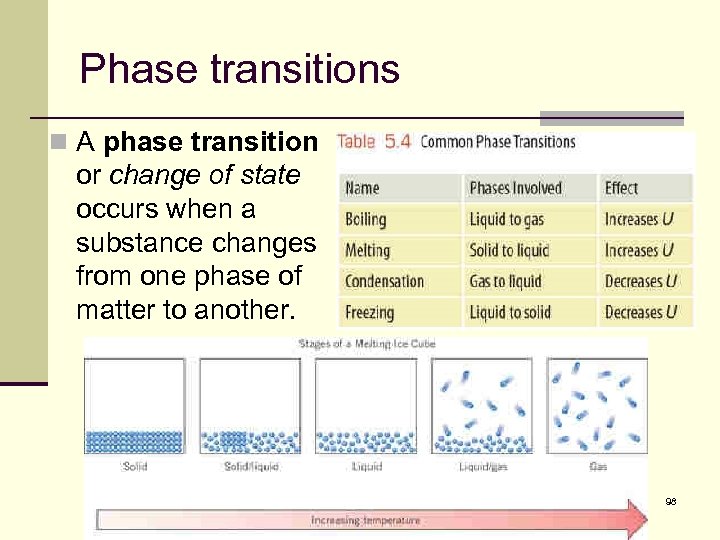 Phase transitions n A phase transition or change of state occurs when a substance changes from one phase of matter to another. 98
Phase transitions n A phase transition or change of state occurs when a substance changes from one phase of matter to another. 98
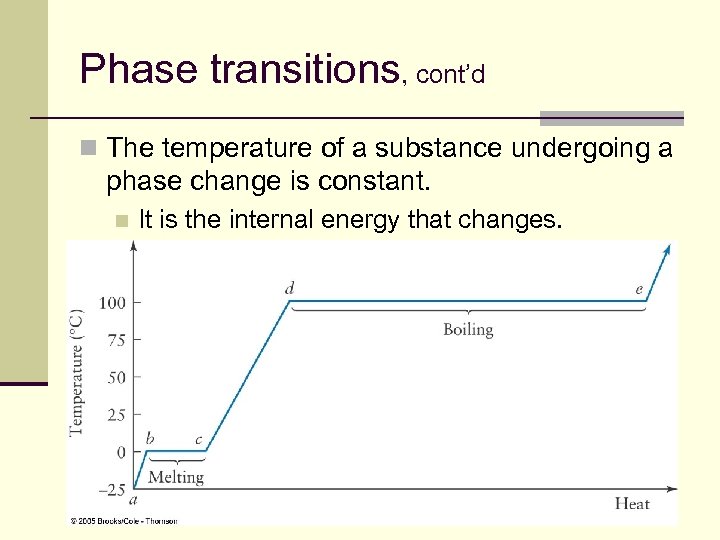 Phase transitions, cont’d n The temperature of a substance undergoing a phase change is constant. n It is the internal energy that changes. 99
Phase transitions, cont’d n The temperature of a substance undergoing a phase change is constant. n It is the internal energy that changes. 99
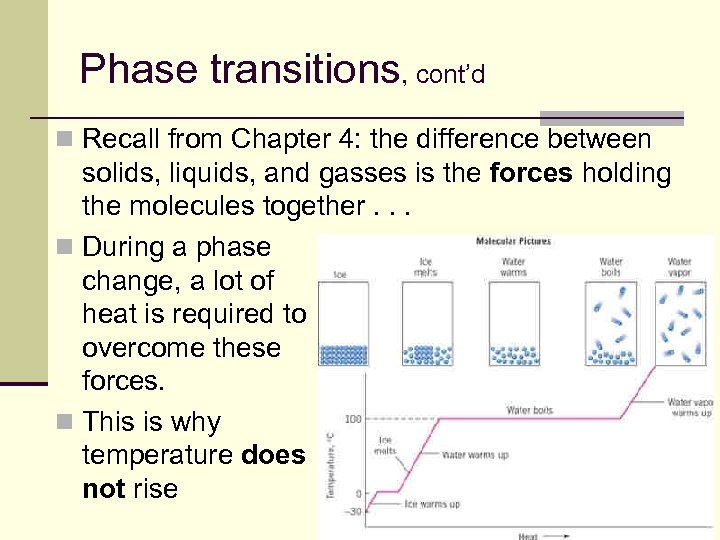 Phase transitions, cont’d n Recall from Chapter 4: the difference between solids, liquids, and gasses is the forces holding the molecules together. . . n During a phase change, a lot of heat is required to overcome these forces. n This is why temperature does not rise 100
Phase transitions, cont’d n Recall from Chapter 4: the difference between solids, liquids, and gasses is the forces holding the molecules together. . . n During a phase change, a lot of heat is required to overcome these forces. n This is why temperature does not rise 100
 Phase transitions, cont’d The phase changes of H 2 O are typical n When you boil water, you increase its temperature and internal energy. n As it changes to water vapor, its internal energy increases but its temperature remains at 100°C. n The energy added to the water overcomes the liquid forces between the molecules together and evaporates the water; it does not increase the molecular kinetic energy (the temperature). n The situation is similar as solid ice undergoes a phase change to water. 101
Phase transitions, cont’d The phase changes of H 2 O are typical n When you boil water, you increase its temperature and internal energy. n As it changes to water vapor, its internal energy increases but its temperature remains at 100°C. n The energy added to the water overcomes the liquid forces between the molecules together and evaporates the water; it does not increase the molecular kinetic energy (the temperature). n The situation is similar as solid ice undergoes a phase change to water. 101
 Phase transitions, cont’d n Melting or freezing 1 kg of ice (2. 2 lb) requires transfer of 334, 000 J of energy. n This amount of energy is called the latent heat of fusion of water. n Boiling or condensing 1 kg of water requires transfer of 2, 260, 000 J of energy. n This amount of energy is called the latent heat of vaporization of water. n Temperature remains constant as heat is added during the phase transition 102
Phase transitions, cont’d n Melting or freezing 1 kg of ice (2. 2 lb) requires transfer of 334, 000 J of energy. n This amount of energy is called the latent heat of fusion of water. n Boiling or condensing 1 kg of water requires transfer of 2, 260, 000 J of energy. n This amount of energy is called the latent heat of vaporization of water. n Temperature remains constant as heat is added during the phase transition 102
 Phase transitions, cont’d n This explains why ice can keep drinks cold in a warm room. Because ice has a high latent heat of fusion, a lot of energy is required to melt ice. n This energy is removed from your drink, keeping it cool. n As long as ice remains in the drink, the temperature stays near 0°C. n 103
Phase transitions, cont’d n This explains why ice can keep drinks cold in a warm room. Because ice has a high latent heat of fusion, a lot of energy is required to melt ice. n This energy is removed from your drink, keeping it cool. n As long as ice remains in the drink, the temperature stays near 0°C. n 103
 Phase transitions, cont’d This explains why water is so efficient fighting fire. n A lot of heat is absorbed raising the temperature to 100 o. C because of high Specific Heat Capacity n Even more heat is absorbed turning water to steam because of high latent heat of vaporization n Six times as much heat is absorbed vaporizing water as raising its temperature from 0 o to 100 o. C 104
Phase transitions, cont’d This explains why water is so efficient fighting fire. n A lot of heat is absorbed raising the temperature to 100 o. C because of high Specific Heat Capacity n Even more heat is absorbed turning water to steam because of high latent heat of vaporization n Six times as much heat is absorbed vaporizing water as raising its temperature from 0 o to 100 o. C 104
 Humidity (last half of Section 5. 6) Lecture will cover only an overview of Humidity – no homework or quiz problems
Humidity (last half of Section 5. 6) Lecture will cover only an overview of Humidity – no homework or quiz problems
 Humidity n At a temperature below their boiling point, liquids gradually go into the gas phase through a process called evaporization. Some liquid molecules escape the liquid’s surface because of their large KE. n At the same time, some vapor molecules are absorbed by the liquid’s surface since they have low KE. n How much liquid evaporates depends upon how many vapor molecules are already in the air. n
Humidity n At a temperature below their boiling point, liquids gradually go into the gas phase through a process called evaporization. Some liquid molecules escape the liquid’s surface because of their large KE. n At the same time, some vapor molecules are absorbed by the liquid’s surface since they have low KE. n How much liquid evaporates depends upon how many vapor molecules are already in the air. n
 Humidity, cont’d n Humidity is the mass of water vapor in the air per unit volume. It is the density of water vapor in the air. n It has the same unit as mass density (kg/m 3). n n At any given temperature, there is a maximum possible humidity called the saturation density. n At the saturation density, the number of water molecules evaporating is equal to the number condensing into liquid water.
Humidity, cont’d n Humidity is the mass of water vapor in the air per unit volume. It is the density of water vapor in the air. n It has the same unit as mass density (kg/m 3). n n At any given temperature, there is a maximum possible humidity called the saturation density. n At the saturation density, the number of water molecules evaporating is equal to the number condensing into liquid water.
 Humidity, cont’d n Saturation density is greater at higher temperatures More water molecules evaporate at higher temperatures. n Dew forms in the morning because temperature falls in the evening, so saturation density is lower. n
Humidity, cont’d n Saturation density is greater at higher temperatures More water molecules evaporate at higher temperatures. n Dew forms in the morning because temperature falls in the evening, so saturation density is lower. n
 Earth’s Thermostat n Saturation Density and water’s high latent heat of vaporization now explain the self-regulation of Earth’s temperature. n Solar Activity is the Primary Contributor to the Earth’s Temperature n There is good correlation between solar activity and Earth’s temperature for hundreds of years. 109
Earth’s Thermostat n Saturation Density and water’s high latent heat of vaporization now explain the self-regulation of Earth’s temperature. n Solar Activity is the Primary Contributor to the Earth’s Temperature n There is good correlation between solar activity and Earth’s temperature for hundreds of years. 109
 Earth’s Thermostat, cont’d n “Greenhouse Effect” – reflection of sunlight by the atmosphere – enhances warming of the Earth. Without it, Earth would average ~0 o. F. n However, if Earth’s temperature were only due to “Greenhouse Effect, ” it would average ~140 o. F n What makes Earth livable? 110
Earth’s Thermostat, cont’d n “Greenhouse Effect” – reflection of sunlight by the atmosphere – enhances warming of the Earth. Without it, Earth would average ~0 o. F. n However, if Earth’s temperature were only due to “Greenhouse Effect, ” it would average ~140 o. F n What makes Earth livable? 110
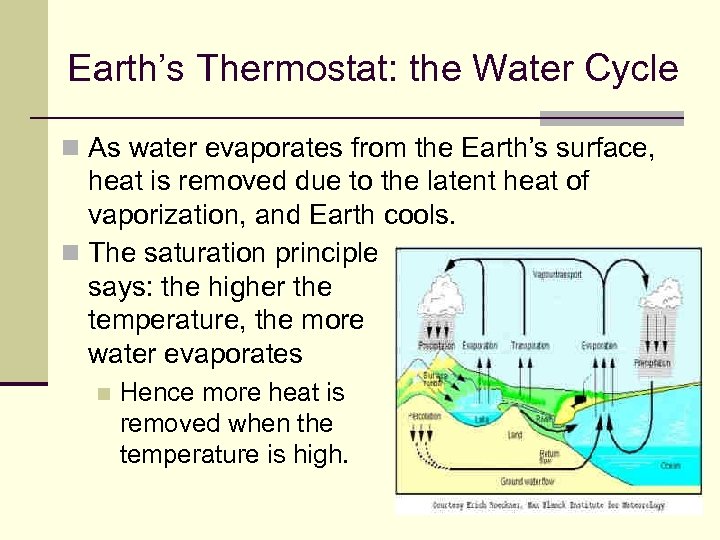 Earth’s Thermostat: the Water Cycle n As water evaporates from the Earth’s surface, heat is removed due to the latent heat of vaporization, and Earth cools. n The saturation principle says: the higher the temperature, the more water evaporates n Hence more heat is removed when the temperature is high.
Earth’s Thermostat: the Water Cycle n As water evaporates from the Earth’s surface, heat is removed due to the latent heat of vaporization, and Earth cools. n The saturation principle says: the higher the temperature, the more water evaporates n Hence more heat is removed when the temperature is high.
 Earth’s Thermostat: the Water Cycle n Water vapor rises into the cooler upper atmosphere n The saturation density is lower, so the vapor condenses into water. n The condensed water forms clouds. . . then rain falls – also cooling the Earth. n The cycle repeats
Earth’s Thermostat: the Water Cycle n Water vapor rises into the cooler upper atmosphere n The saturation density is lower, so the vapor condenses into water. n The condensed water forms clouds. . . then rain falls – also cooling the Earth. n The cycle repeats
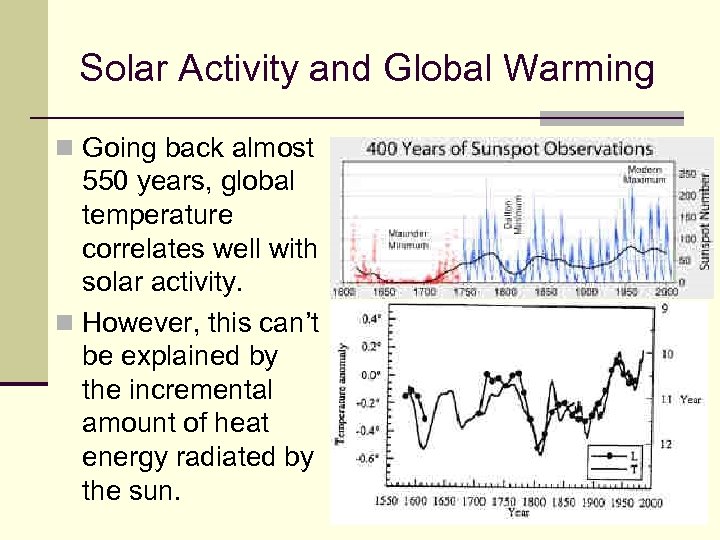 Solar Activity and Global Warming n Going back almost 550 years, global temperature correlates well with solar activity. n However, this can’t be explained by the incremental amount of heat energy radiated by the sun. 113
Solar Activity and Global Warming n Going back almost 550 years, global temperature correlates well with solar activity. n However, this can’t be explained by the incremental amount of heat energy radiated by the sun. 113
 Solar Activity and Global Warming, cont’d Experiments now show this is explained by the effect of solar radiation on cloud formation. n A 2011 experiment at CERN* confirmed a 1997 study** which showed that : Cosmic rays striking atmospheric water vapor, liberate electrons which provide the necessary seeding to form clouds. n Increased solar radiation deflects cosmic rays, and fewer clouds are formed. n n Temperature increases *Kirkby et al, “Role of Sulphuric acid, ammonia, and galactic cosmic rays in atmospheric aerosol nucleation, 114 Nature, 476 (25 Aug 2011), 429 -433. **Svensmark and Friis-Christensen, “Variation of Cosmic Ray Flux and Global Cloud Cover, ” JASTP 59, 11 (1997) 1225 -1232
Solar Activity and Global Warming, cont’d Experiments now show this is explained by the effect of solar radiation on cloud formation. n A 2011 experiment at CERN* confirmed a 1997 study** which showed that : Cosmic rays striking atmospheric water vapor, liberate electrons which provide the necessary seeding to form clouds. n Increased solar radiation deflects cosmic rays, and fewer clouds are formed. n n Temperature increases *Kirkby et al, “Role of Sulphuric acid, ammonia, and galactic cosmic rays in atmospheric aerosol nucleation, 114 Nature, 476 (25 Aug 2011), 429 -433. **Svensmark and Friis-Christensen, “Variation of Cosmic Ray Flux and Global Cloud Cover, ” JASTP 59, 11 (1997) 1225 -1232
 Solar Activity and Global Warming n Hence high solar activity causes fewer clouds, reducing the cooling effect of the Earth’s natural thermostat – and the Earth warms. n Reduced solar activity allows more clouds, and the Earth cools. n A principle flaw in theory of anthropogenic Global Warming is that the computer models do not account for the effects of clouds. * n Moreover, since water vapor is a greenhouse gas, global warming advocates predict clouds should be a warming influence (holding heat in) – but experiment shows this is NOT the case. 115 *IPCC Report, 1992
Solar Activity and Global Warming n Hence high solar activity causes fewer clouds, reducing the cooling effect of the Earth’s natural thermostat – and the Earth warms. n Reduced solar activity allows more clouds, and the Earth cools. n A principle flaw in theory of anthropogenic Global Warming is that the computer models do not account for the effects of clouds. * n Moreover, since water vapor is a greenhouse gas, global warming advocates predict clouds should be a warming influence (holding heat in) – but experiment shows this is NOT the case. 115 *IPCC Report, 1992
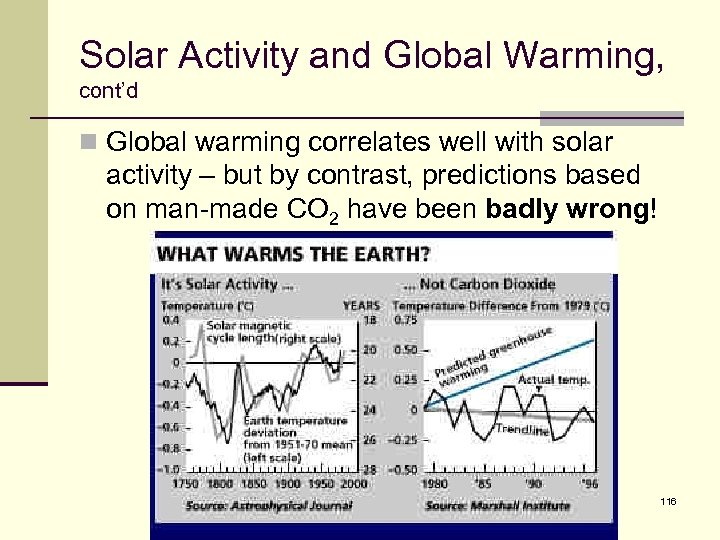 Solar Activity and Global Warming, cont’d n Global warming correlates well with solar activity – but by contrast, predictions based on man-made CO 2 have been badly wrong! 116
Solar Activity and Global Warming, cont’d n Global warming correlates well with solar activity – but by contrast, predictions based on man-made CO 2 have been badly wrong! 116
 Global Warming “Fraud” Released October 13, 2010. . . “Global warming is the greatest and most successful pseudoscientific fraud I have seen in my long life”* – Physicist Harold Lewis In APS resignation letter http: //blogs. telegraph. co. uk/news/jamesdelingpole/100058265/us-physics-professor-global-warming-is-the-greatest-and-most-successful-pseudoscientific-fraud-i-have-seen-in-my-long-life/
Global Warming “Fraud” Released October 13, 2010. . . “Global warming is the greatest and most successful pseudoscientific fraud I have seen in my long life”* – Physicist Harold Lewis In APS resignation letter http: //blogs. telegraph. co. uk/news/jamesdelingpole/100058265/us-physics-professor-global-warming-is-the-greatest-and-most-successful-pseudoscientific-fraud-i-have-seen-in-my-long-life/
 Man-Made Global Warming Hoax n 1079 emails and 72 documents leaked from Britain’s Climate Research Unit in November 2009 suggest “conspiracy, collusion in exaggerating warming data, possibly illegal destruction of embarrassing information, organized resistance to disclosure, manipulation of data, private admissions of flaws in their public claims and much more. ” n Called “the greatest [scandal] in modern science. ” http: //www. dailymail. co. uk/debate/article-1230113/The-devastating-book-debunks-climate-change. html http: //blogs. telegraph. co. uk/news/jamesdelingpole/100017393/climategate-the-final-nail-in-the-coffin-of-anthropogenic-global-warming/ http: //online. wsj. com/article/SB 125883405294859215. html? mod=WSJ_hpp_sections_news http: //www. nytimes. com/2009/11/21/science/earth/21 climate. html? _r=3&hp
Man-Made Global Warming Hoax n 1079 emails and 72 documents leaked from Britain’s Climate Research Unit in November 2009 suggest “conspiracy, collusion in exaggerating warming data, possibly illegal destruction of embarrassing information, organized resistance to disclosure, manipulation of data, private admissions of flaws in their public claims and much more. ” n Called “the greatest [scandal] in modern science. ” http: //www. dailymail. co. uk/debate/article-1230113/The-devastating-book-debunks-climate-change. html http: //blogs. telegraph. co. uk/news/jamesdelingpole/100017393/climategate-the-final-nail-in-the-coffin-of-anthropogenic-global-warming/ http: //online. wsj. com/article/SB 125883405294859215. html? mod=WSJ_hpp_sections_news http: //www. nytimes. com/2009/11/21/science/earth/21 climate. html? _r=3&hp
 Global Warming Hoax, cont’d n CO 2 is a miniscule percentage of the atmosphere n About 0. 03% or 300 parts per million (ppm). n Intuitively, it would take a lot of additional CO 2 to have much impact – especially with the water cycle thermostat. 119
Global Warming Hoax, cont’d n CO 2 is a miniscule percentage of the atmosphere n About 0. 03% or 300 parts per million (ppm). n Intuitively, it would take a lot of additional CO 2 to have much impact – especially with the water cycle thermostat. 119
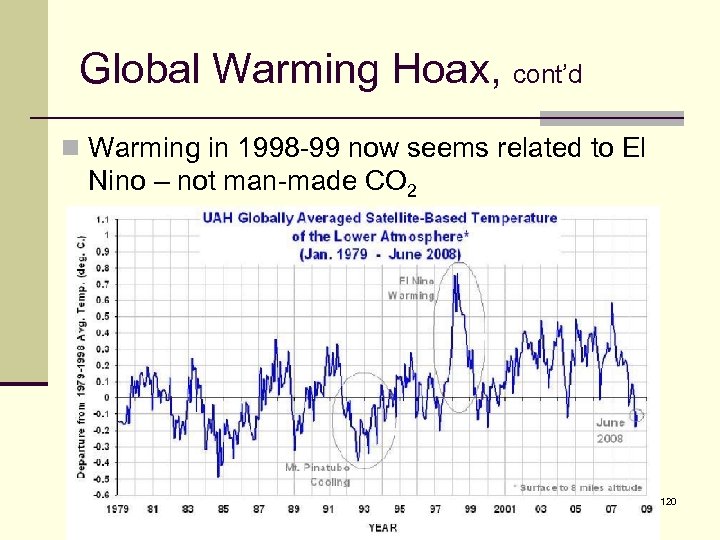 Global Warming Hoax, cont’d n Warming in 1998 -99 now seems related to El Nino – not man-made CO 2 120
Global Warming Hoax, cont’d n Warming in 1998 -99 now seems related to El Nino – not man-made CO 2 120
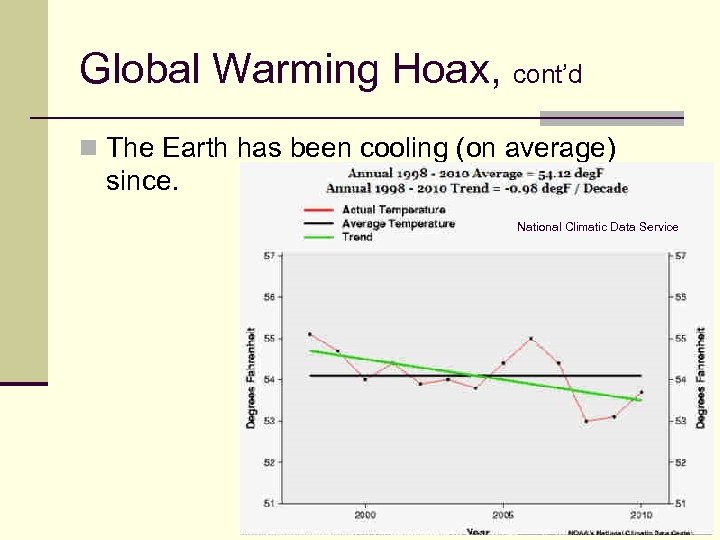 Global Warming Hoax, cont’d n The Earth has been cooling (on average) since. National Climatic Data Service
Global Warming Hoax, cont’d n The Earth has been cooling (on average) since. National Climatic Data Service
 Glaciers Advancing in Alaska n Terminus of Tsaa Glacier in Icy Bay in July 2005 n Terminus of Tsaa Glacier in June 2007. . . advanced ~. 33 mile http: //www. iceagenow. com/Growing_Glaciers. htm 122
Glaciers Advancing in Alaska n Terminus of Tsaa Glacier in Icy Bay in July 2005 n Terminus of Tsaa Glacier in June 2007. . . advanced ~. 33 mile http: //www. iceagenow. com/Growing_Glaciers. htm 122
 But What if Global Warming is Real? n Even if temperatures do rise over the next century, most scientists believe the rise will be very slight – consistent with temperature fluctuations over the past 4500 years (next slide). n This is reflected in IPCC reports n If sea levels do rise, they will be by inches – not feet. Mankind has confronted such a rise over the past century; we know how to deal with it.
But What if Global Warming is Real? n Even if temperatures do rise over the next century, most scientists believe the rise will be very slight – consistent with temperature fluctuations over the past 4500 years (next slide). n This is reflected in IPCC reports n If sea levels do rise, they will be by inches – not feet. Mankind has confronted such a rise over the past century; we know how to deal with it.
 Phase Transitions and Pressure n Boiling point proportional to pressure n A pressure of 2 atm raises boiling point of water to 120 o. C n This is why a pressure cooker works n The temperature of the food in the pressure cooker is higher than 100 o. C 124
Phase Transitions and Pressure n Boiling point proportional to pressure n A pressure of 2 atm raises boiling point of water to 120 o. C n This is why a pressure cooker works n The temperature of the food in the pressure cooker is higher than 100 o. C 124
 Second Law of Thermodynamics “The Supreme Law of Nature” —Arthur Eddington, Astrophysicist
Second Law of Thermodynamics “The Supreme Law of Nature” —Arthur Eddington, Astrophysicist
 Second Law of Thermodynamics The 2 nd Law of Thermodynamics is complex. We describe using three examples: n Heat Engines n Heat Movers n Entropy
Second Law of Thermodynamics The 2 nd Law of Thermodynamics is complex. We describe using three examples: n Heat Engines n Heat Movers n Entropy
 Heat engines and the 2 nd law of thermodynamics n A heat engine is a device that transforms heat into mechanical energy or work. It absorbs heat from a hot source (such as burning fuel), n Converts some of this energy into usable mechanical energy or work, and n Outputs the remaining energy as heat to a lower-temperature reservoir. n 127
Heat engines and the 2 nd law of thermodynamics n A heat engine is a device that transforms heat into mechanical energy or work. It absorbs heat from a hot source (such as burning fuel), n Converts some of this energy into usable mechanical energy or work, and n Outputs the remaining energy as heat to a lower-temperature reservoir. n 127
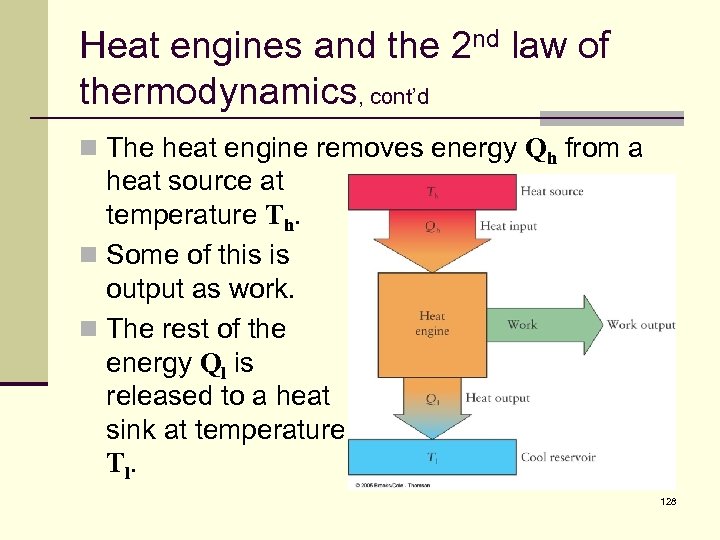 Heat engines and the 2 nd law of thermodynamics, cont’d n The heat engine removes energy Qh from a heat source at temperature Th. n Some of this is output as work. n The rest of the energy Ql is released to a heat sink at temperature T l. 128
Heat engines and the 2 nd law of thermodynamics, cont’d n The heat engine removes energy Qh from a heat source at temperature Th. n Some of this is output as work. n The rest of the energy Ql is released to a heat sink at temperature T l. 128
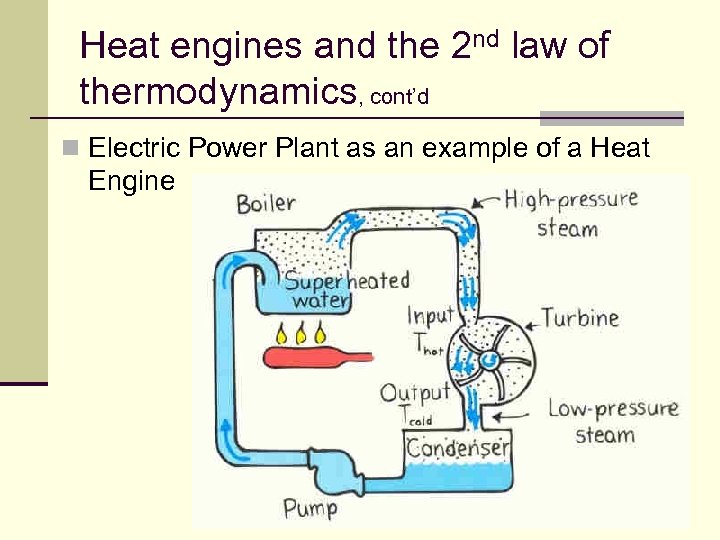 Heat engines and the 2 nd law of thermodynamics, cont’d n Electric Power Plant as an example of a Heat Engine 129
Heat engines and the 2 nd law of thermodynamics, cont’d n Electric Power Plant as an example of a Heat Engine 129
 Heat engines and the 2 nd law of thermodynamics, cont’d n Gasoline and diesel engines are heat engines. n They convert some of the heat released from burning a fuel into mechanical energy. . . yet release additional heat into the air. 130 2 Cycle Diesel 4 Cycle Gasoline Engine
Heat engines and the 2 nd law of thermodynamics, cont’d n Gasoline and diesel engines are heat engines. n They convert some of the heat released from burning a fuel into mechanical energy. . . yet release additional heat into the air. 130 2 Cycle Diesel 4 Cycle Gasoline Engine
 Heat engines and the 2 nd law of thermodynamics, cont’d n The Second Law of Thermodynamics states that no device can be built that will repeatedly extract heat from a source and deliver mechanical work or energy without ejecting some heat to a lower-temperature reservoir. n This means that you cannot create a device of perfect efficiency. n n Some energy will be wasted. A perpetual motion machine is impossible. 131
Heat engines and the 2 nd law of thermodynamics, cont’d n The Second Law of Thermodynamics states that no device can be built that will repeatedly extract heat from a source and deliver mechanical work or energy without ejecting some heat to a lower-temperature reservoir. n This means that you cannot create a device of perfect efficiency. n n Some energy will be wasted. A perpetual motion machine is impossible. 131
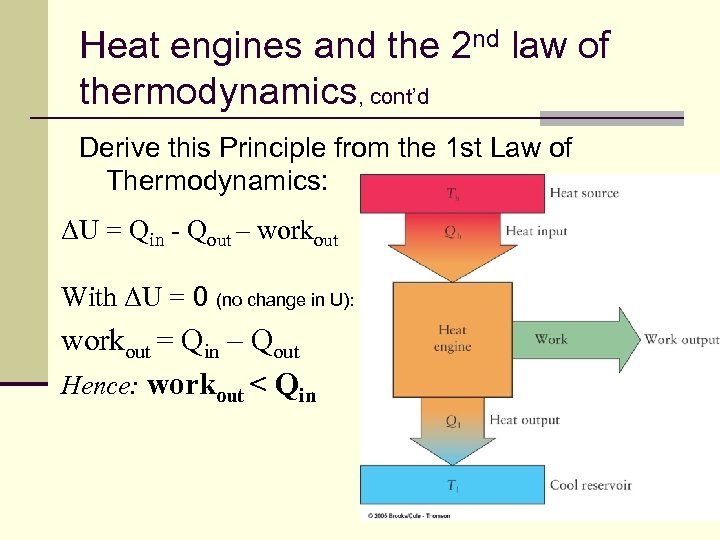 Heat engines and the 2 nd law of thermodynamics, cont’d Derive this Principle from the 1 st Law of Thermodynamics: ΔU = Qin - Qout – workout With ΔU = 0 (no change in U): workout = Qin – Qout Hence: workout < Qin 132
Heat engines and the 2 nd law of thermodynamics, cont’d Derive this Principle from the 1 st Law of Thermodynamics: ΔU = Qin - Qout – workout With ΔU = 0 (no change in U): workout = Qin – Qout Hence: workout < Qin 132
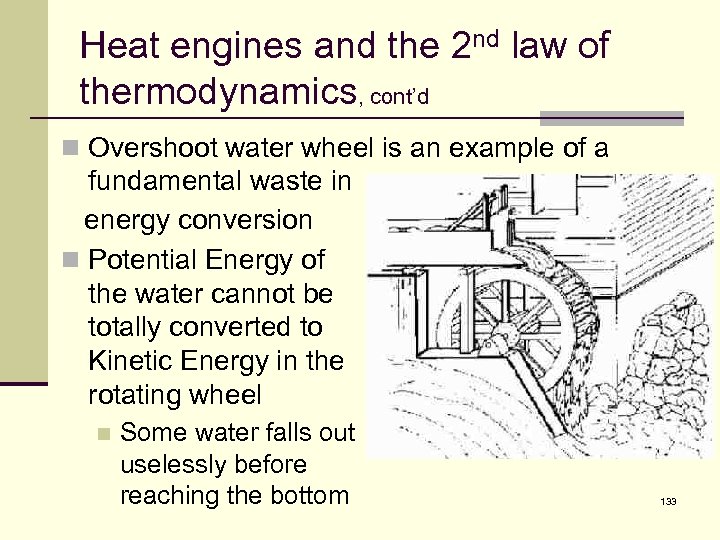 Heat engines and the 2 nd law of thermodynamics, cont’d n Overshoot water wheel is an example of a fundamental waste in energy conversion n Potential Energy of the water cannot be totally converted to Kinetic Energy in the rotating wheel n Some water falls out uselessly before reaching the bottom 133
Heat engines and the 2 nd law of thermodynamics, cont’d n Overshoot water wheel is an example of a fundamental waste in energy conversion n Potential Energy of the water cannot be totally converted to Kinetic Energy in the rotating wheel n Some water falls out uselessly before reaching the bottom 133
 Heat engines and the 2 nd law of thermodynamics, cont’d n The efficiency of any device can be written: n If the efficiency is 25% then only ¼ of the input energy is available in a usable form. 134
Heat engines and the 2 nd law of thermodynamics, cont’d n The efficiency of any device can be written: n If the efficiency is 25% then only ¼ of the input energy is available in a usable form. 134
 Heat engines and the 2 nd law of thermodynamics, cont’d n For heat engines, we can write the efficiency: n Qh is the energy input to the heat engine. 135
Heat engines and the 2 nd law of thermodynamics, cont’d n For heat engines, we can write the efficiency: n Qh is the energy input to the heat engine. 135
 Heat engines and the 2 nd law of thermodynamics, cont’d n There is a fundamental upper limit to the maximum efficiency of a heat engine. n This maximum energy is called the Carnot efficiency: n The temperatures must be expressed in Kelvin. 136
Heat engines and the 2 nd law of thermodynamics, cont’d n There is a fundamental upper limit to the maximum efficiency of a heat engine. n This maximum energy is called the Carnot efficiency: n The temperatures must be expressed in Kelvin. 136
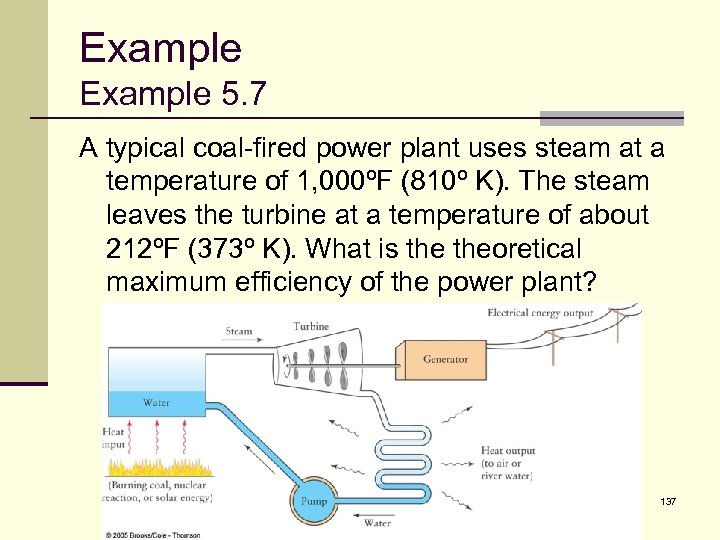 Example 5. 7 A typical coal-fired power plant uses steam at a temperature of 1, 000ºF (810º K). The steam leaves the turbine at a temperature of about 212ºF (373º K). What is theoretical maximum efficiency of the power plant? 137
Example 5. 7 A typical coal-fired power plant uses steam at a temperature of 1, 000ºF (810º K). The steam leaves the turbine at a temperature of about 212ºF (373º K). What is theoretical maximum efficiency of the power plant? 137
 Example 5. 5 ANSWER: The problem gives us: The Carnot efficiency is then 138
Example 5. 5 ANSWER: The problem gives us: The Carnot efficiency is then 138
 Example 5. 4 DISCUSSION: This is the ideal efficiency. Normal efficiencies are around 35 -40%. Almost two out of three coal carloads are wasted! It’s not man’s fault – it’s a Law of Nature 139
Example 5. 4 DISCUSSION: This is the ideal efficiency. Normal efficiencies are around 35 -40%. Almost two out of three coal carloads are wasted! It’s not man’s fault – it’s a Law of Nature 139
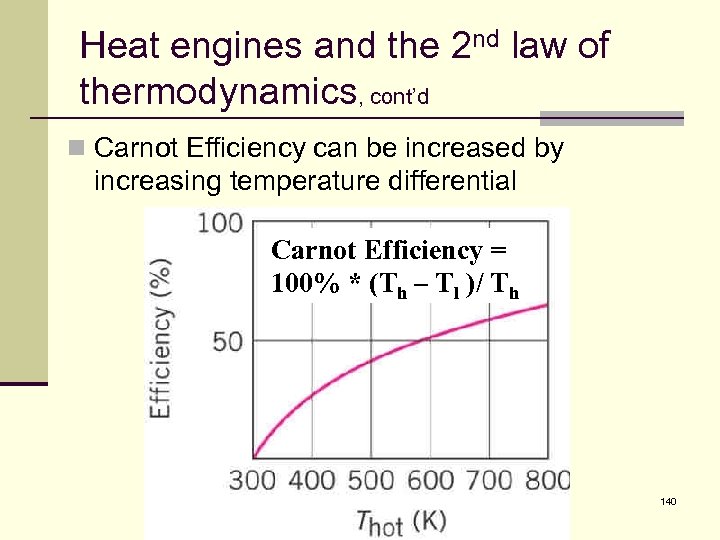 Heat engines and the 2 nd law of thermodynamics, cont’d n Carnot Efficiency can be increased by increasing temperature differential Carnot Efficiency = 100% * (Th – Tl )/ Th 140
Heat engines and the 2 nd law of thermodynamics, cont’d n Carnot Efficiency can be increased by increasing temperature differential Carnot Efficiency = 100% * (Th – Tl )/ Th 140
 Heat movers and the 2 nd law of thermodynamics n Recall. . . heat flows from a hotter substance to a colder substance, never the reverse n However, we can make this happen by adding energy to a heat mover 141
Heat movers and the 2 nd law of thermodynamics n Recall. . . heat flows from a hotter substance to a colder substance, never the reverse n However, we can make this happen by adding energy to a heat mover 141
 Heat movers and the 2 nd law of thermodynamics, cont’d n A heat mover is a device that acts like a heat engine in reverse. n It uses an external energy source to move heat from a cooler substance to a warmer substance. n Examples are refrigerators, air conditioners, heat pumps, etc. 142
Heat movers and the 2 nd law of thermodynamics, cont’d n A heat mover is a device that acts like a heat engine in reverse. n It uses an external energy source to move heat from a cooler substance to a warmer substance. n Examples are refrigerators, air conditioners, heat pumps, etc. 142
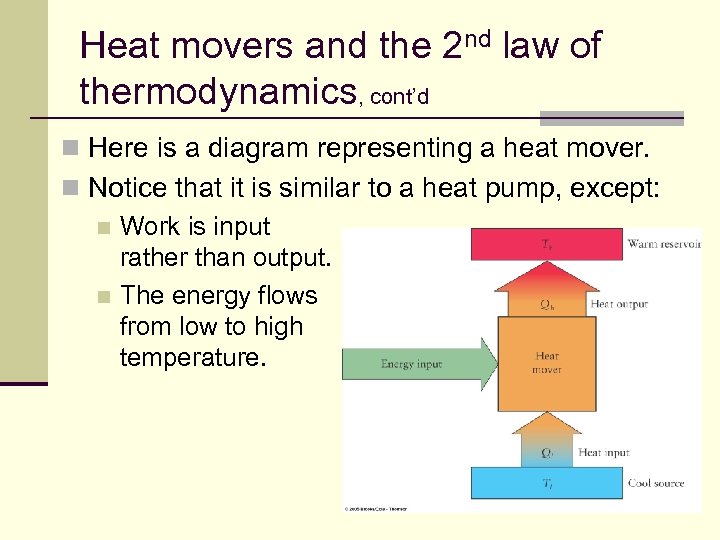 Heat movers and the 2 nd law of thermodynamics, cont’d n Here is a diagram representing a heat mover. n Notice that it is similar to a heat pump, except: n Work is input rather than output. n The energy flows from low to high temperature. 143
Heat movers and the 2 nd law of thermodynamics, cont’d n Here is a diagram representing a heat mover. n Notice that it is similar to a heat pump, except: n Work is input rather than output. n The energy flows from low to high temperature. 143
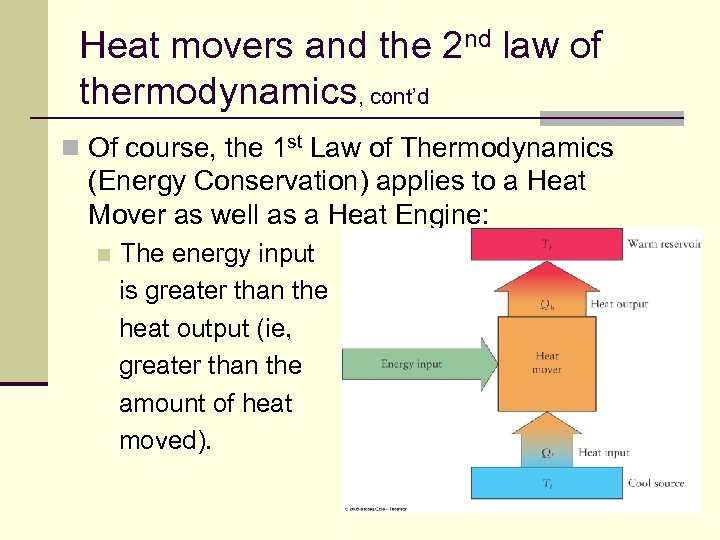 Heat movers and the 2 nd law of thermodynamics, cont’d n Of course, the 1 st Law of Thermodynamics (Energy Conservation) applies to a Heat Mover as well as a Heat Engine: n The energy input is greater than the heat output (ie, greater than the amount of heat moved). 144
Heat movers and the 2 nd law of thermodynamics, cont’d n Of course, the 1 st Law of Thermodynamics (Energy Conservation) applies to a Heat Mover as well as a Heat Engine: n The energy input is greater than the heat output (ie, greater than the amount of heat moved). 144
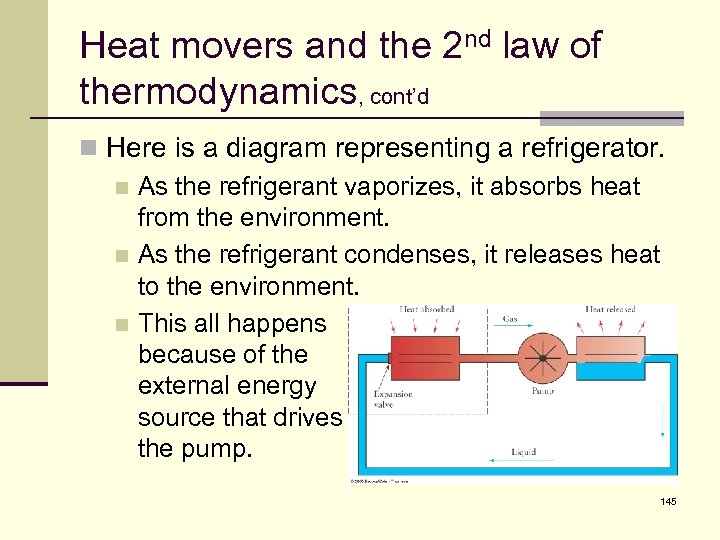 Heat movers and the 2 nd law of thermodynamics, cont’d n Here is a diagram representing a refrigerator. n As the refrigerant vaporizes, it absorbs heat from the environment. n As the refrigerant condenses, it releases heat to the environment. n This all happens because of the external energy source that drives the pump. 145
Heat movers and the 2 nd law of thermodynamics, cont’d n Here is a diagram representing a refrigerator. n As the refrigerant vaporizes, it absorbs heat from the environment. n As the refrigerant condenses, it releases heat to the environment. n This all happens because of the external energy source that drives the pump. 145
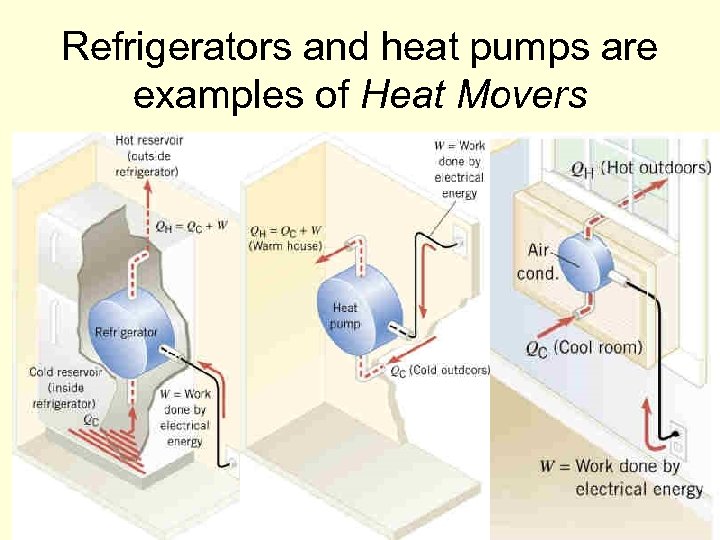 Refrigerators and heat pumps are examples of Heat Movers 146
Refrigerators and heat pumps are examples of Heat Movers 146
 Entropy and the 2 nd law of thermodynamics n Consider the principles of Order and Disorder 147
Entropy and the 2 nd law of thermodynamics n Consider the principles of Order and Disorder 147
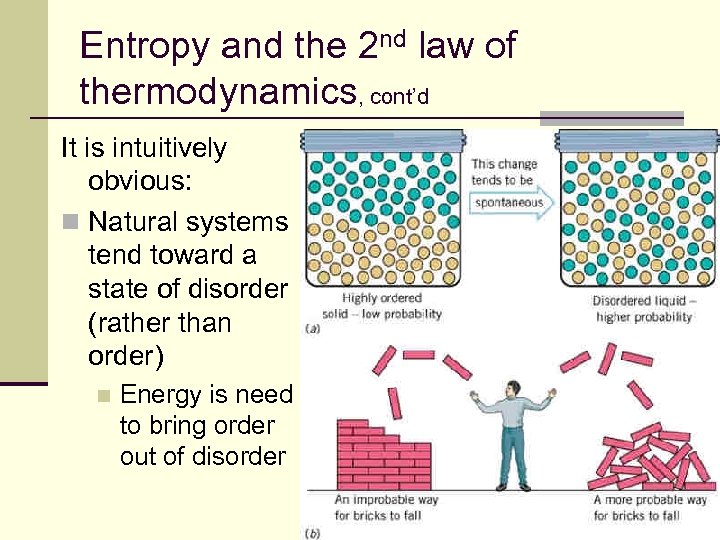 Entropy and the 2 nd law of thermodynamics, cont’d It is intuitively obvious: n Natural systems tend toward a state of disorder (rather than order) n Energy is need to bring order out of disorder 148
Entropy and the 2 nd law of thermodynamics, cont’d It is intuitively obvious: n Natural systems tend toward a state of disorder (rather than order) n Energy is need to bring order out of disorder 148
 Entropy and the 2 nd law of thermodynamics, cont’d n Define a quantity Entropy which represents the amount of disorder in the system. . . or the waste when energy is converted from one form to another n The Entropy of an isolated system never decreases. The entropy of the universe is constantly increasing 149
Entropy and the 2 nd law of thermodynamics, cont’d n Define a quantity Entropy which represents the amount of disorder in the system. . . or the waste when energy is converted from one form to another n The Entropy of an isolated system never decreases. The entropy of the universe is constantly increasing 149
 The 2 nd Law of Thermodynamics n Perpetual motion machines are impossible – there is always waste with every energy transfer (Heat Engines/Carnot Efficiency) n Heat can be made to flow from a colder body to a hotter body – but energy must be added to make this happen (Heat Movers) n Natural processes tend to increase the disorder of systems – but order can be achieved by adding energy (Entropy) 150
The 2 nd Law of Thermodynamics n Perpetual motion machines are impossible – there is always waste with every energy transfer (Heat Engines/Carnot Efficiency) n Heat can be made to flow from a colder body to a hotter body – but energy must be added to make this happen (Heat Movers) n Natural processes tend to increase the disorder of systems – but order can be achieved by adding energy (Entropy) 150
 Second Law of Thermodynamics “The Supreme Law of Nature” —Arthur Eddington, Astrophysicist
Second Law of Thermodynamics “The Supreme Law of Nature” —Arthur Eddington, Astrophysicist
 Laws of Thermodynamics First Law n “You can’t win” Second Law n “You can’t even break even” 152
Laws of Thermodynamics First Law n “You can’t win” Second Law n “You can’t even break even” 152
![Important Equations AAA Temperature Conversion: [Ko] = [Co] + 273 o 153 Important Equations AAA Temperature Conversion: [Ko] = [Co] + 273 o 153](https://present5.com/presentation/63762d74fc639cbc3caa42d6e76ce4c6/image-153.jpg) Important Equations AAA Temperature Conversion: [Ko] = [Co] + 273 o 153
Important Equations AAA Temperature Conversion: [Ko] = [Co] + 273 o 153
 END
END


