Photonic Topological Insulators Y Plotnik 1 J M

Photonic Topological Insulators Y. Plotnik 1, J. M. Zeuner 2, M. C. Rechtsman 1, Y. Lumer 1, S. Nolte 2, M. Segev 1, A. Szameit 2 1 Department of Physics, Technion – Israel Institute of Technology, Haifa, Israel 2 Institute of Applied Physics, Friedrich-Schiller-Universität, Jena, Germany

Outline -What are Topological Insulators? -Topological protection of photons? -How can we get unidirectional edge states in photonics? Floquet! -Description of our experimental system: photonic lattices -First observation of topological insulators -This is also the first observation of optical unidirectional edge states in optics! -Future directions

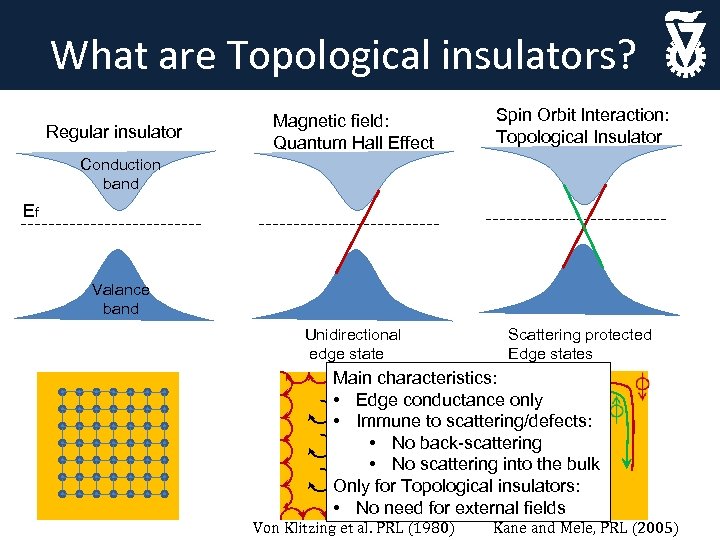What are Topological insulators? Regular insulator Magnetic field: Quantum Hall Effect Spin Orbit Interaction: Topological Insulator Unidirectional edge state Scattering protected Edge states Conduction band Ef Valance band Main characteristics: • Edge conductance only • Immune to scattering/defects: • No back-scattering • No scattering into the bulk Only for Topological insulators: • No need for external fields Von Klitzing et al. PRL (1980) Kane and Mele, PRL (2005)

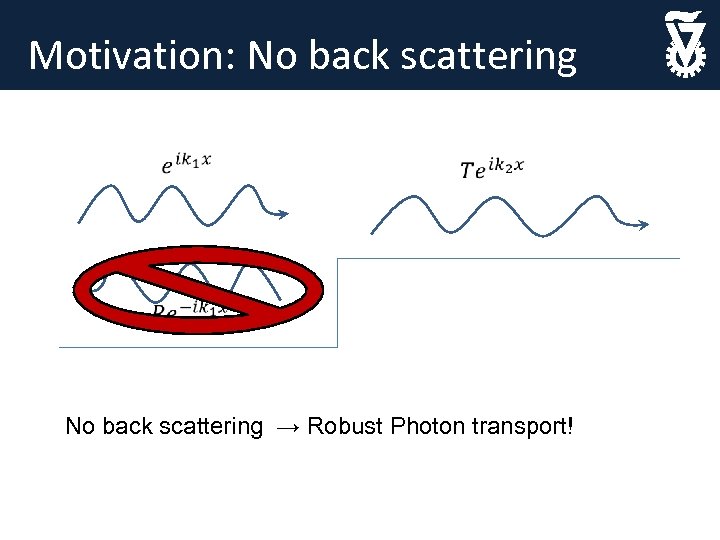Motivation: No back scattering → Robust Photon transport!

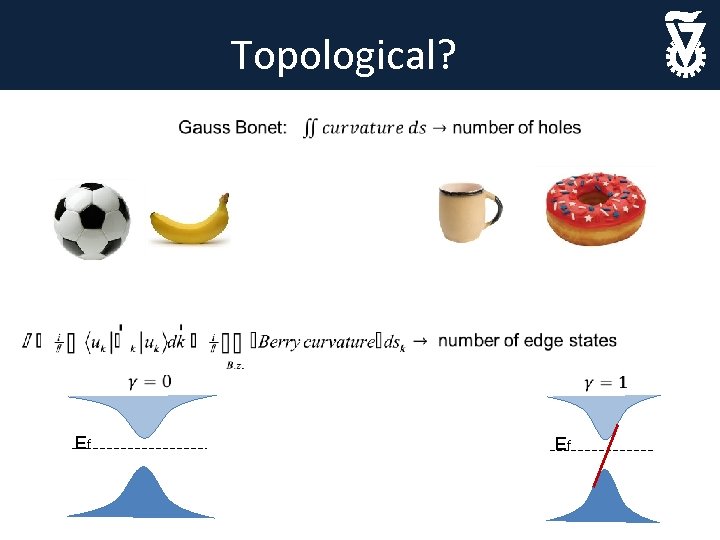Topological? Ef

Background: photonic topological protection by magnetic field For optical frequencies, magnetic response is weak Raghu, Haldane PRL (2008) Unidirectional edge state: Wang et. al. Nature (2009) Wang et. al. , PRL (2008)

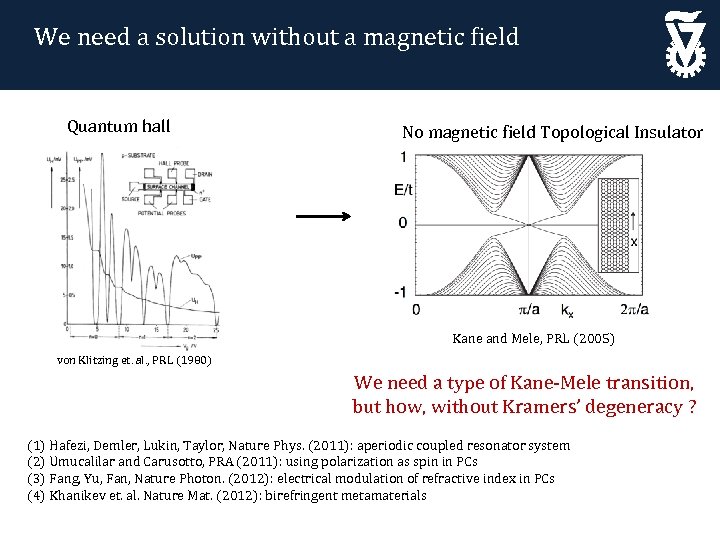We need a solution without a magnetic field Quantum hall No magnetic field Topological Insulator Kane and Mele, PRL (2005) von Klitzing et. al. , PRL (1980) We need a type of Kane-Mele transition, but how, without Kramers’ degeneracy ? (1) Hafezi, Demler, Lukin, Taylor, Nature Phys. (2011): aperiodic coupled resonator system (2) Umucalilar and Carusotto, PRA (2011): using polarization as spin in PCs (3) Fang, Yu, Fan, Nature Photon. (2012): electrical modulation of refractive index in PCs (4) Khanikev et. al. Nature Mat. (2012): birefringent metamaterials

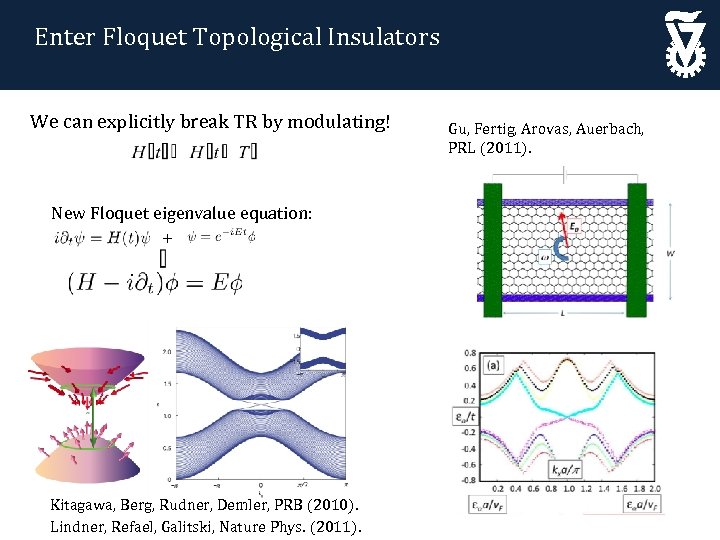Enter Floquet Topological Insulators We can explicitly break TR by modulating! New Floquet eigenvalue equation: + Kitagawa, Berg, Rudner, Demler, PRB (2010). Lindner, Refael, Galitski, Nature Phys. (2011). Gu, Fertig, Arovas, Auerbach, PRL (2011).

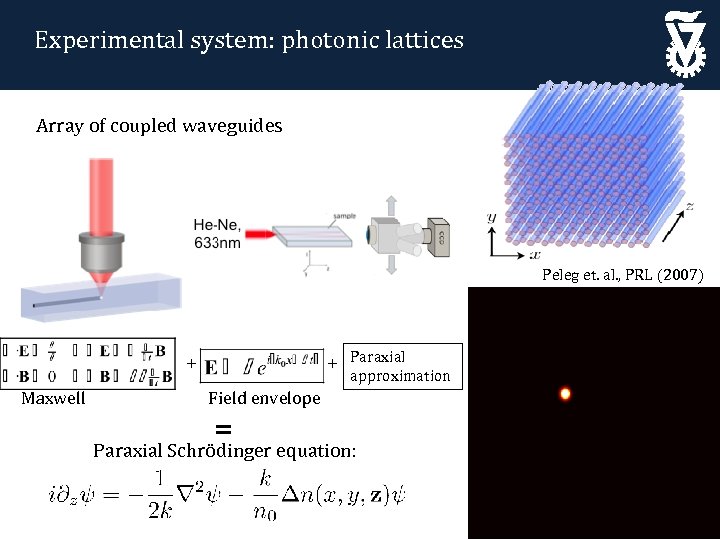Experimental system: photonic lattices Array of coupled waveguides Peleg et. al. , PRL (2007) + Paraxial + Maxwell approximation Field envelope = equation: Paraxial Schrödinger

Helical rotation induces a gauge field Paraxial Schrödinger equation Coordinate Transformation + Tight Binding Model (Peierls substitution)

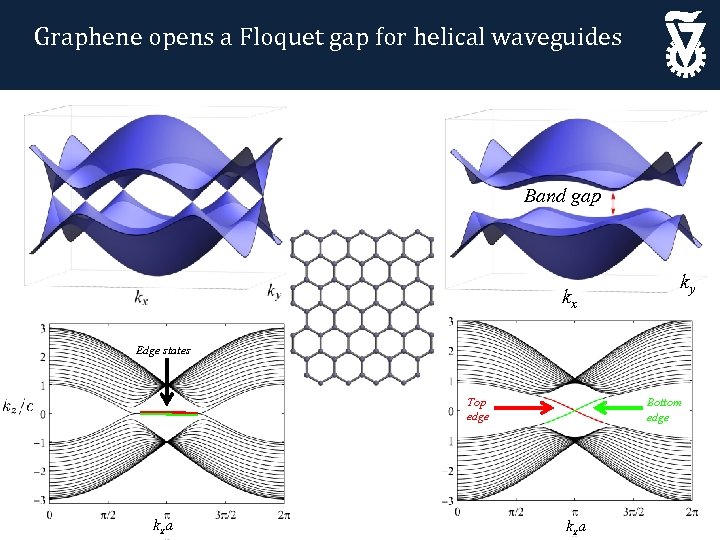Graphene opens a Floquet gap for helical waveguides Band gap kx ky Edge states Top edge kxa Bottom edge kxa

Experimental results: rectangular arrays Microscope image - No scattering from the corner - Armchair edge confinement

“Time”-domain simulations

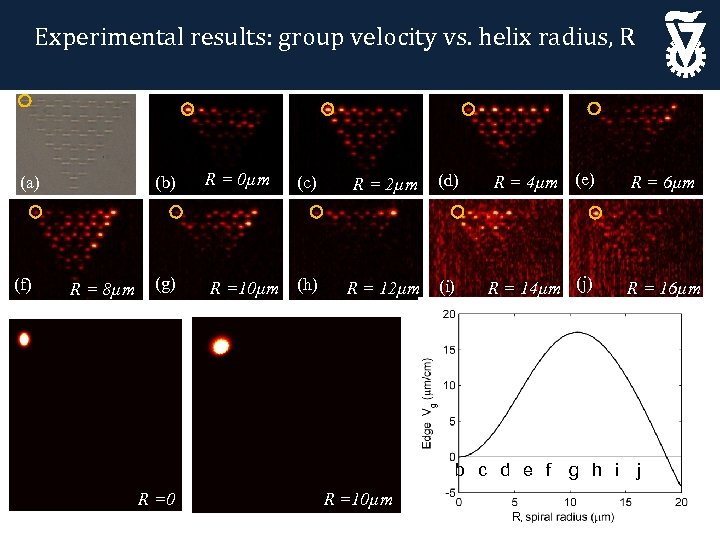Experimental results: group velocity vs. helix radius, R (b) (a) (f) R = 8µm R = 0µm (c) R = 2µm (d) R = 4µm (e) R = 6µm (g) R =10µm (h) R = 12µm (i) R = 14µm (j) R = 16µm b c d e f g h i R =0 R =10µm R, j

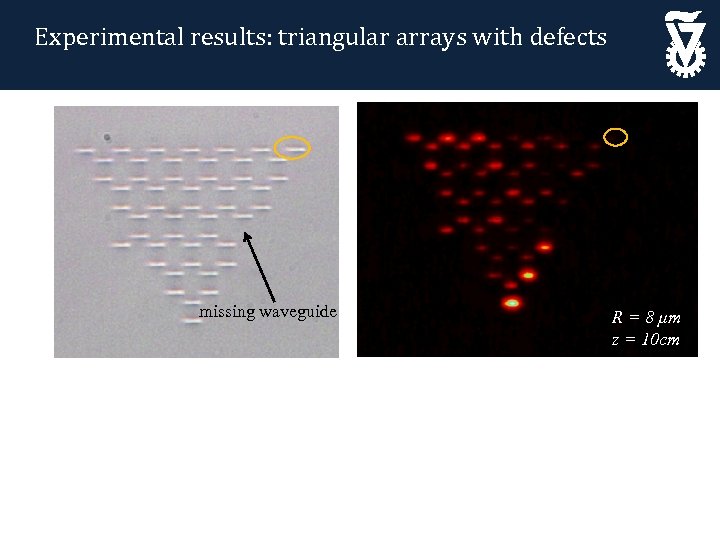Experimental results: triangular arrays with defects missing waveguide R = 8 µm z = 10 cm

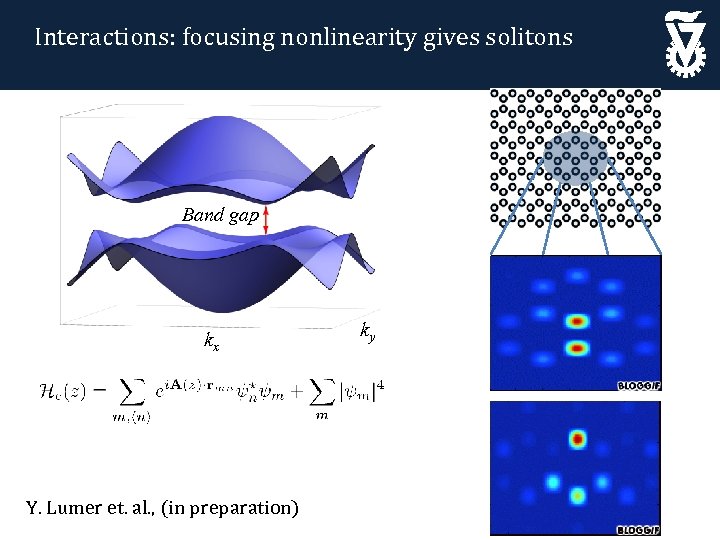Interactions: focusing nonlinearity gives solitons Band gap kx Y. Lumer et. al. , (in preparation) ky

Conclusion and Future work - First Optical Topological Insulator - First robust one way optical edge states (without any magnetic field!) Future Work: - Non-scattering in optoelectronics - Topological cloak? - Disorder: Topological Anderson insulator? - What effect do interactions have on edge states? - many modes on-site.

Acknowledgments Discussions: Daniel Podolsky

Challenge of scaling down: Faraday effect is weak Faraday effect Largest Verdet constant (e. g. in TGG) is ~100 Optical wavelengths are the key to all nanophotonics applications The effect is too weak. We need another way!

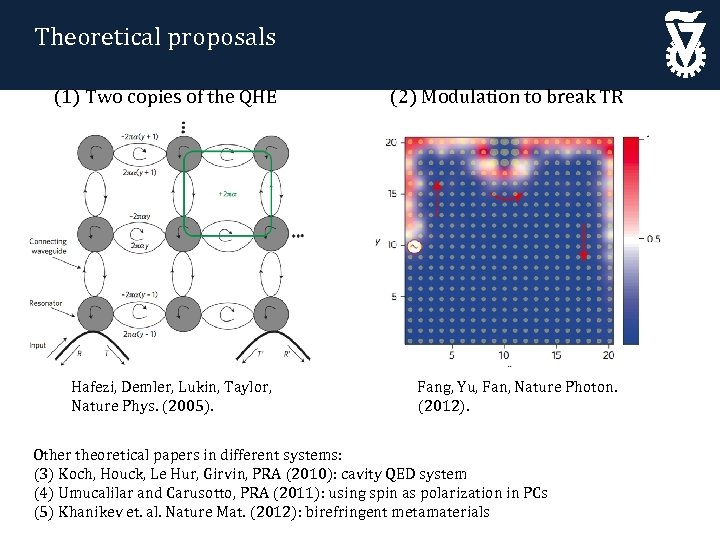Theoretical proposals (1) Two copies of the QHE Hafezi, Demler, Lukin, Taylor, Nature Phys. (2005). (2) Modulation to break TR Fang, Yu, Fan, Nature Photon. (2012). Other theoretical papers in different systems: (3) Koch, Houck, Le Hur, Girvin, PRA (2010): cavity QED system (4) Umucalilar and Carusotto, PRA (2011): using spin as polarization in PCs (5) Khanikev et. al. Nature Mat. (2012): birefringent metamaterials