fd87c10738217e8340d6ae89fbe9bd97.ppt
- Количество слайдов: 65
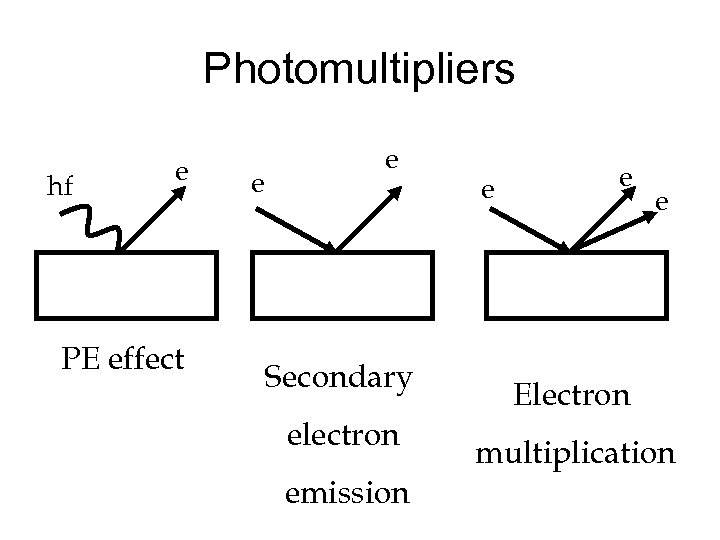 Photomultipliers hf e PE effect e e Secondary electron emission e e e Electron multiplication
Photomultipliers hf e PE effect e e Secondary electron emission e e e Electron multiplication
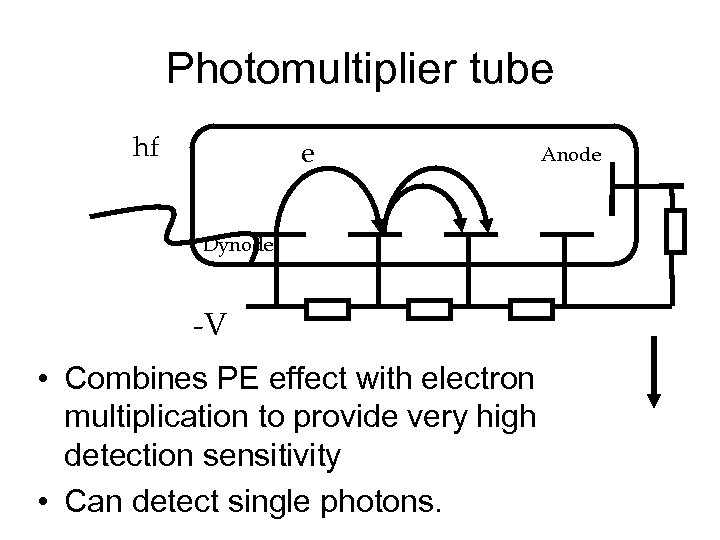 Photomultiplier tube hf e Dynode -V • Combines PE effect with electron multiplication to provide very high detection sensitivity • Can detect single photons. Anode
Photomultiplier tube hf e Dynode -V • Combines PE effect with electron multiplication to provide very high detection sensitivity • Can detect single photons. Anode
 Microchannel plates • The principle of the photomultiplier tube can be extended to an array of photomultipliers • This way one can obtain spatial resolution • Biggest application is in night vision goggles for military and civilian use
Microchannel plates • The principle of the photomultiplier tube can be extended to an array of photomultipliers • This way one can obtain spatial resolution • Biggest application is in night vision goggles for military and civilian use
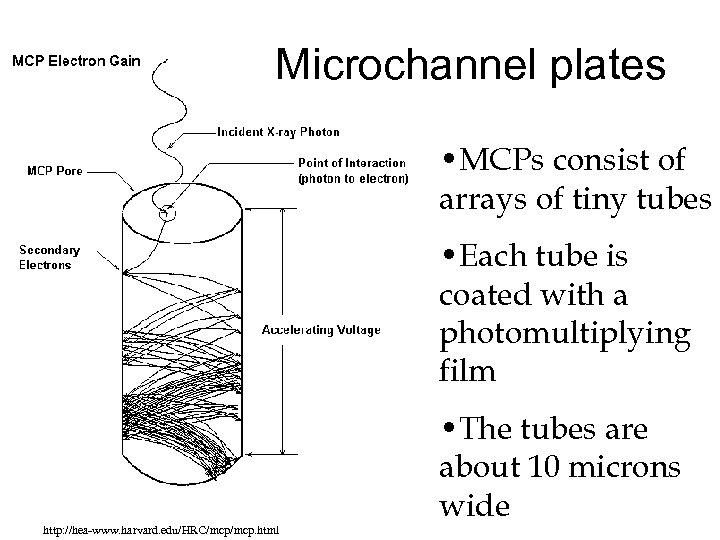 Microchannel plates • MCPs consist of arrays of tiny tubes • Each tube is coated with a photomultiplying film http: //hea-www. harvard. edu/HRC/mcp. html • The tubes are about 10 microns wide
Microchannel plates • MCPs consist of arrays of tiny tubes • Each tube is coated with a photomultiplying film http: //hea-www. harvard. edu/HRC/mcp. html • The tubes are about 10 microns wide
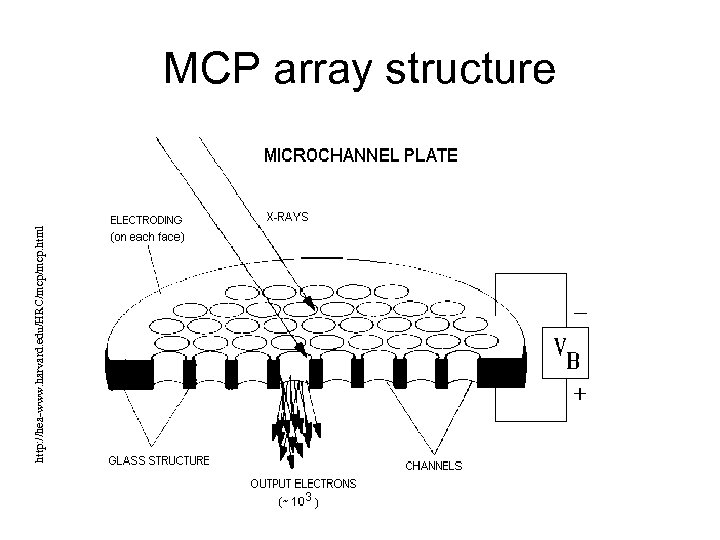 http: //hea-www. harvard. edu/HRC/mcp. html MCP array structure
http: //hea-www. harvard. edu/HRC/mcp. html MCP array structure
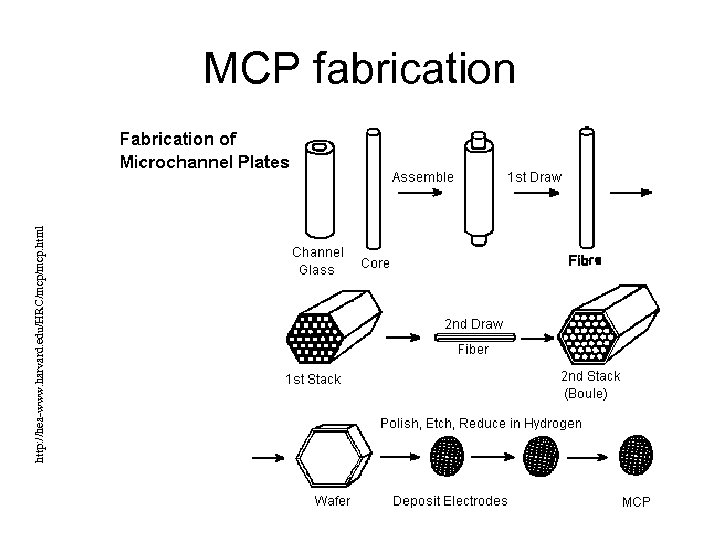 http: //hea-www. harvard. edu/HRC/mcp. html MCP fabrication
http: //hea-www. harvard. edu/HRC/mcp. html MCP fabrication
 Disadvantages of Photomultiplers as sensors • Need expensive and fiddly high vacuum equipment • Expensive • Fragile • Bulky
Disadvantages of Photomultiplers as sensors • Need expensive and fiddly high vacuum equipment • Expensive • Fragile • Bulky
 Photoconductors • As well as liberating electrons from the surface of materials, we can excite mobile electrons inside materials • The most useful class of materials to do this are semiconductors • The mobile electrons can be measured as a current proportional to the intensity of the incident radiation • Need to understand semiconductors….
Photoconductors • As well as liberating electrons from the surface of materials, we can excite mobile electrons inside materials • The most useful class of materials to do this are semiconductors • The mobile electrons can be measured as a current proportional to the intensity of the incident radiation • Need to understand semiconductors….
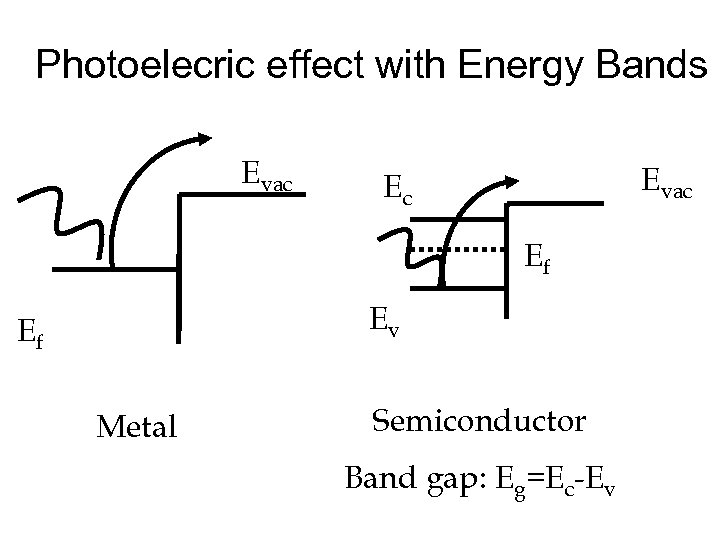 Photoelecric effect with Energy Bands Evac Ec Ef Ev Ef Metal Semiconductor Band gap: Eg=Ec-Ev
Photoelecric effect with Energy Bands Evac Ec Ef Ev Ef Metal Semiconductor Band gap: Eg=Ec-Ev
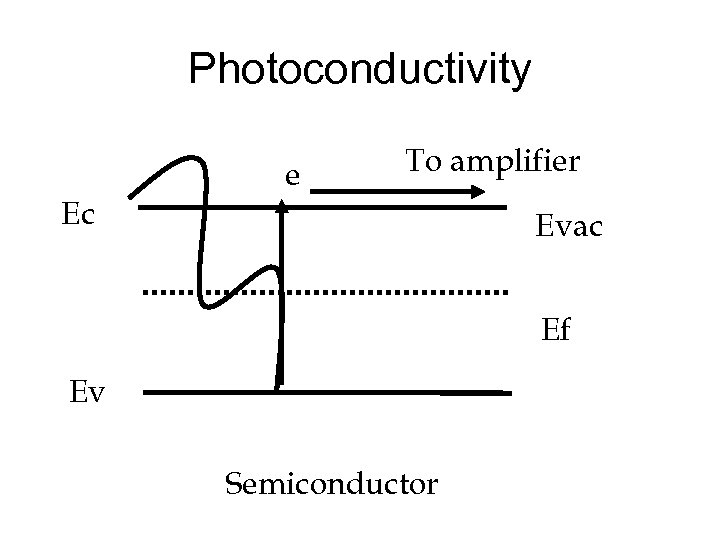 Photoconductivity Ec e To amplifier Evac Ef Ev Semiconductor
Photoconductivity Ec e To amplifier Evac Ef Ev Semiconductor
 Photoconductors • Eg (~1 e. V) can be made smaller than metal work functions f (~5 e. V) • Only photons with Energy E=hf>Eg are detected • This puts a lower limit on the frequency detected • Broadly speaking, metals work with UV, semiconductors with optical
Photoconductors • Eg (~1 e. V) can be made smaller than metal work functions f (~5 e. V) • Only photons with Energy E=hf>Eg are detected • This puts a lower limit on the frequency detected • Broadly speaking, metals work with UV, semiconductors with optical
 Band gap Engineering • Semiconductors can be made with a band gap tailored for a particular frequency, depending on the application. • Wide band gap semiconductors good for UV light • III-V semiconductors promising new materials
Band gap Engineering • Semiconductors can be made with a band gap tailored for a particular frequency, depending on the application. • Wide band gap semiconductors good for UV light • III-V semiconductors promising new materials
 Example: A Ga. N based UV detector This is a photoconductor 5 m
Example: A Ga. N based UV detector This is a photoconductor 5 m
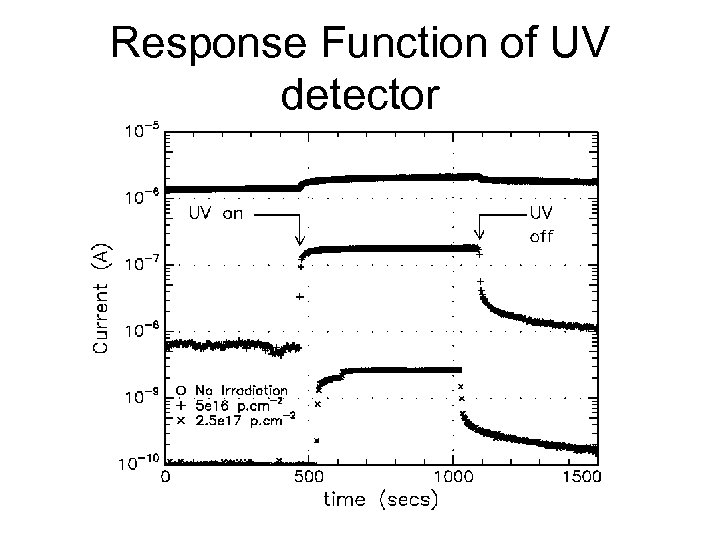 Response Function of UV detector
Response Function of UV detector
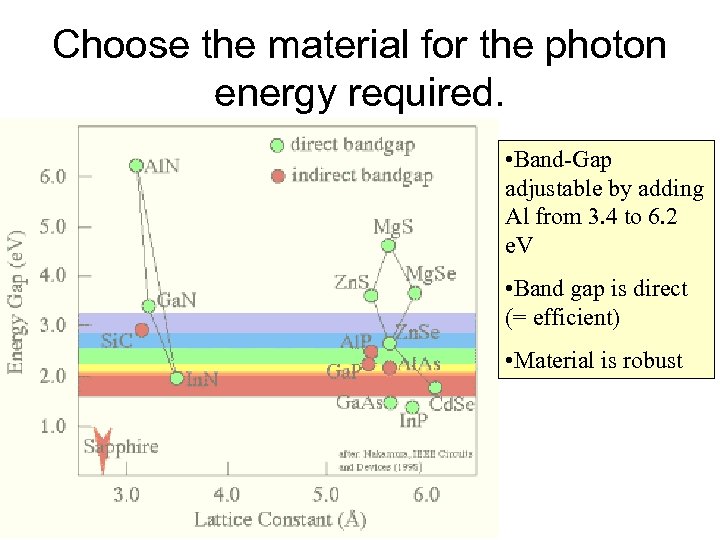 Choose the material for the photon energy required. • Band-Gap adjustable by adding Al from 3. 4 to 6. 2 e. V • Band gap is direct (= efficient) • Material is robust
Choose the material for the photon energy required. • Band-Gap adjustable by adding Al from 3. 4 to 6. 2 e. V • Band gap is direct (= efficient) • Material is robust
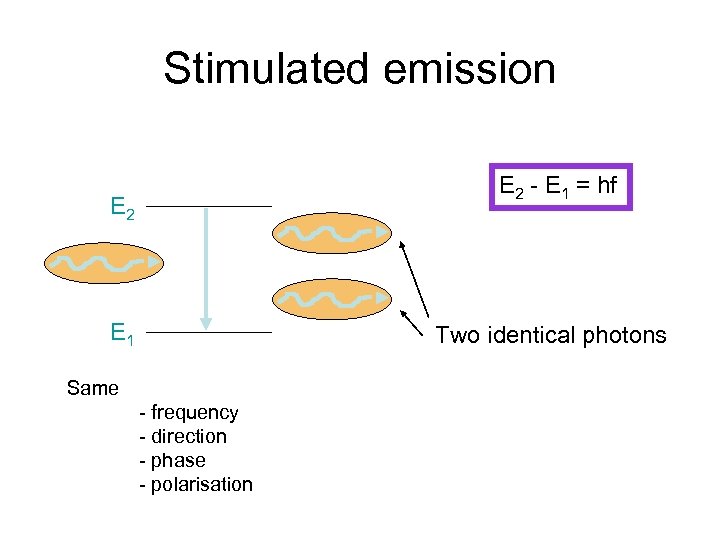 Stimulated emission E 2 - E 1 = hf E 2 E 1 Two identical photons Same - frequency - direction - phase - polarisation
Stimulated emission E 2 - E 1 = hf E 2 E 1 Two identical photons Same - frequency - direction - phase - polarisation
 Lasers • LASER - acronym for – Light Amplification by Stimulated Emission of Radiation – produce high intensity power at a single frequency (i. e. monochromatic)
Lasers • LASER - acronym for – Light Amplification by Stimulated Emission of Radiation – produce high intensity power at a single frequency (i. e. monochromatic)
 Principles of Lasers • Usually have more atoms in low(est) energy levels • Atomic systems can be pumped so that more atoms are in a higher energy level. • Requires input of energy • Called Population Inversion: achieved via • Electric discharge • Optically • Direct current
Principles of Lasers • Usually have more atoms in low(est) energy levels • Atomic systems can be pumped so that more atoms are in a higher energy level. • Requires input of energy • Called Population Inversion: achieved via • Electric discharge • Optically • Direct current
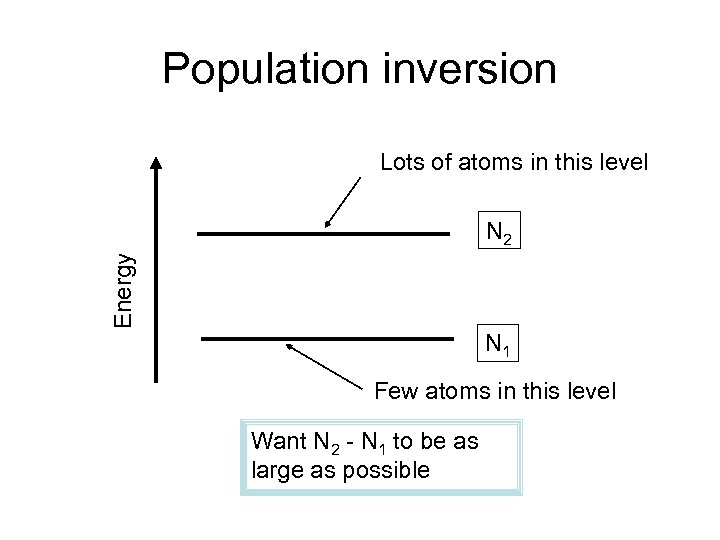 Population inversion Lots of atoms in this level Energy N 2 N 1 Few atoms in this level Want N 2 - N 1 to be as large as possible
Population inversion Lots of atoms in this level Energy N 2 N 1 Few atoms in this level Want N 2 - N 1 to be as large as possible
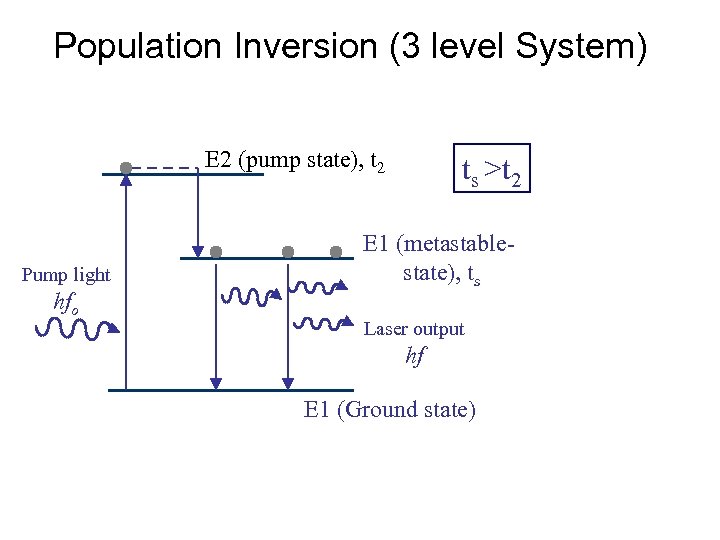 Population Inversion (3 level System) E 2 (pump state), t 2 Pump light hfo ts >t 2 E 1 (metastable state), ts Laser output hf E 1 (Ground state)
Population Inversion (3 level System) E 2 (pump state), t 2 Pump light hfo ts >t 2 E 1 (metastable state), ts Laser output hf E 1 (Ground state)
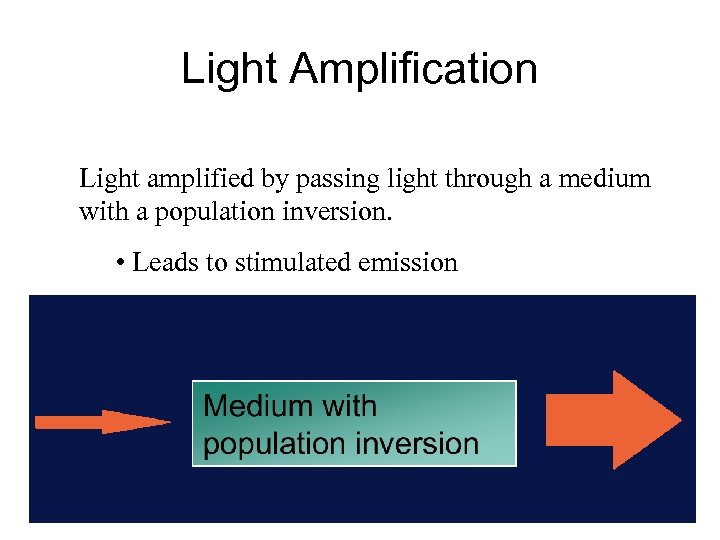 Light Amplification Light amplified by passing light through a medium with a population inversion. • Leads to stimulated emission
Light Amplification Light amplified by passing light through a medium with a population inversion. • Leads to stimulated emission
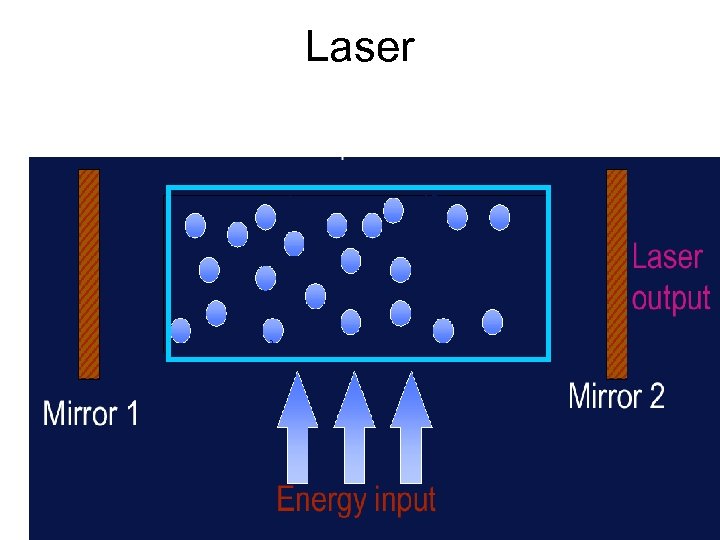 Laser
Laser
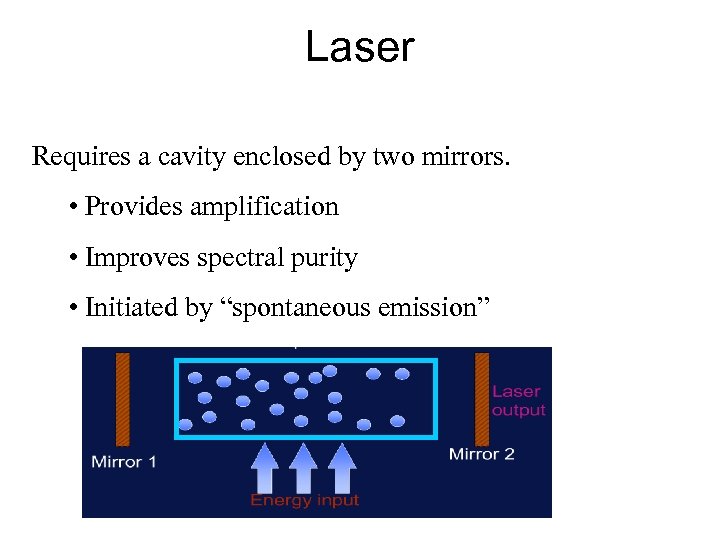 Laser Requires a cavity enclosed by two mirrors. • Provides amplification • Improves spectral purity • Initiated by “spontaneous emission”
Laser Requires a cavity enclosed by two mirrors. • Provides amplification • Improves spectral purity • Initiated by “spontaneous emission”
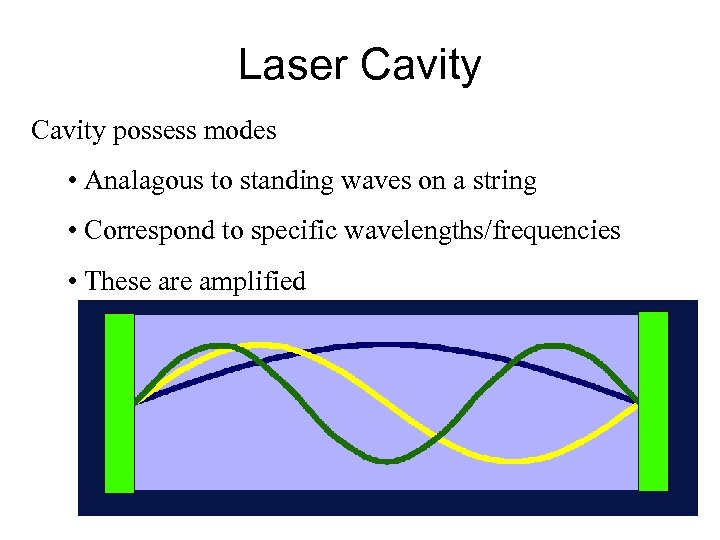 Laser Cavity possess modes • Analagous to standing waves on a string • Correspond to specific wavelengths/frequencies • These are amplified
Laser Cavity possess modes • Analagous to standing waves on a string • Correspond to specific wavelengths/frequencies • These are amplified
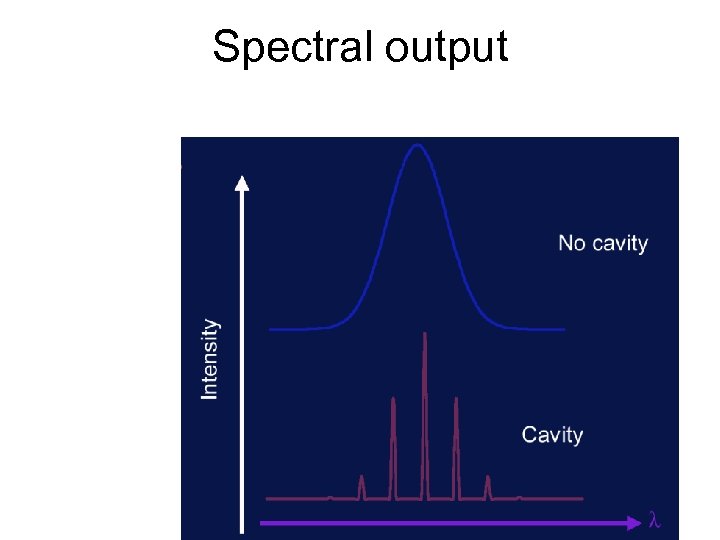 Spectral output
Spectral output
 Properties of Laser Light. • Can be monochromatic • Coherent • Very intense • Short pulses can be produced
Properties of Laser Light. • Can be monochromatic • Coherent • Very intense • Short pulses can be produced
 Types of Lasers Large range of wavelengths available: • Ammonia (microwave) MASER • CO 2 (far infrared) • Semiconductor (near-infrared, visible) • Helium-Neon (visible) • Ar. F – excimer (ultraviolet) • Soft x-ray (free-electron, experimental)
Types of Lasers Large range of wavelengths available: • Ammonia (microwave) MASER • CO 2 (far infrared) • Semiconductor (near-infrared, visible) • Helium-Neon (visible) • Ar. F – excimer (ultraviolet) • Soft x-ray (free-electron, experimental)
 Optical Fibre Sensors • • Non-Electrical Explosion-Proof (Often) Non-contact Light, small, snakey => “Remotable” Easy(ish) to install Immune to most EM noise Solid-State (no moving parts) Multiplexing/distributed sensors.
Optical Fibre Sensors • • Non-Electrical Explosion-Proof (Often) Non-contact Light, small, snakey => “Remotable” Easy(ish) to install Immune to most EM noise Solid-State (no moving parts) Multiplexing/distributed sensors.
 Applications • • Lots of Temp, Pressure, Chemistry Automated production lines/processes Automotive (T, P, Ch, Flow) Avionic (T, P, Disp, rotn, strain, liquid level) Climate control (T, P, Flow) Appliances (T, P) Environmental (Disp, T, P)
Applications • • Lots of Temp, Pressure, Chemistry Automated production lines/processes Automotive (T, P, Ch, Flow) Avionic (T, P, Disp, rotn, strain, liquid level) Climate control (T, P, Flow) Appliances (T, P) Environmental (Disp, T, P)
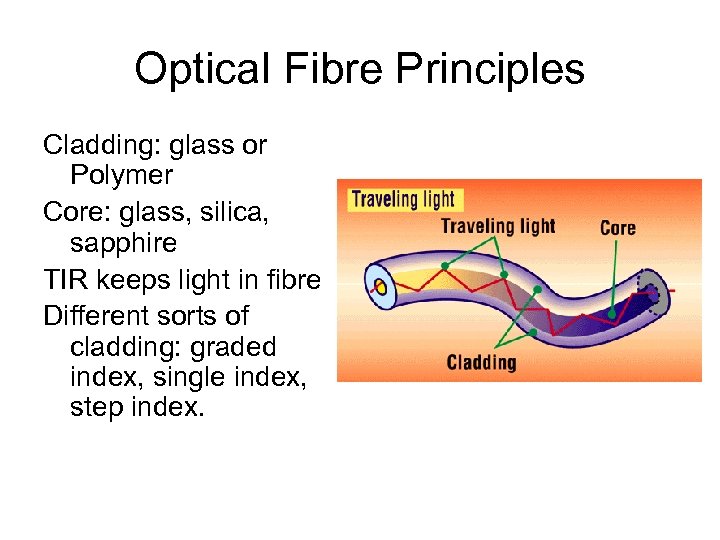 Optical Fibre Principles Cladding: glass or Polymer Core: glass, silica, sapphire TIR keeps light in fibre Different sorts of cladding: graded index, single index, step index.
Optical Fibre Principles Cladding: glass or Polymer Core: glass, silica, sapphire TIR keeps light in fibre Different sorts of cladding: graded index, single index, step index.


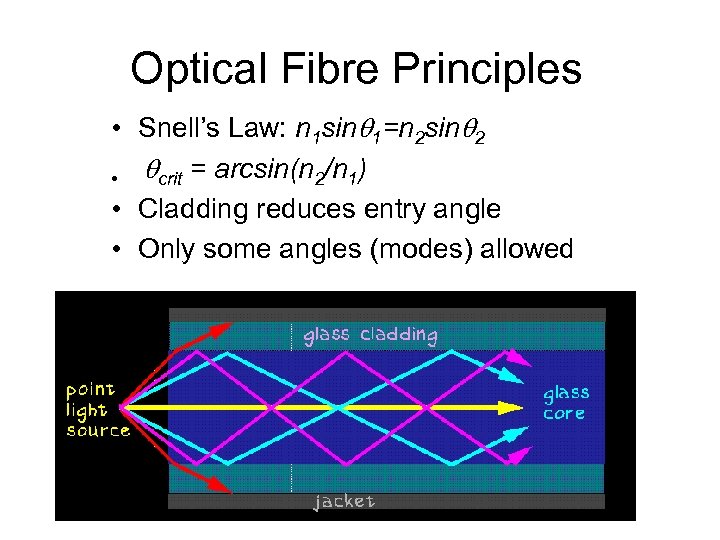 Optical Fibre Principles • Snell’s Law: n 1 sin 1=n 2 sin 2 • crit = arcsin(n 2/n 1) • Cladding reduces entry angle • Only some angles (modes) allowed
Optical Fibre Principles • Snell’s Law: n 1 sin 1=n 2 sin 2 • crit = arcsin(n 2/n 1) • Cladding reduces entry angle • Only some angles (modes) allowed
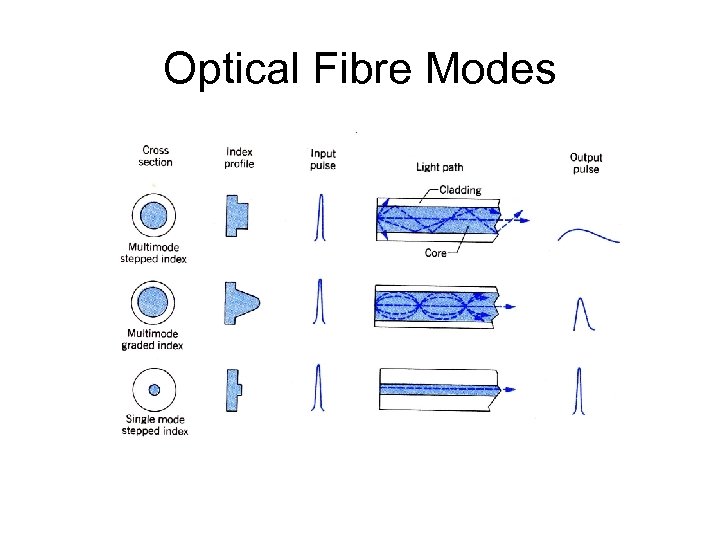 Optical Fibre Modes
Optical Fibre Modes
 Phase and Intensity Modulation methods • Optical fibre sensors fall into two types: – Intensity modulation uses the change in the amount of light that reaches a detector, say by breaking a fibre. – Phase Modulation uses the interference between two beams to detect tiny differences in path length, e. g. by thermal expansion.
Phase and Intensity Modulation methods • Optical fibre sensors fall into two types: – Intensity modulation uses the change in the amount of light that reaches a detector, say by breaking a fibre. – Phase Modulation uses the interference between two beams to detect tiny differences in path length, e. g. by thermal expansion.
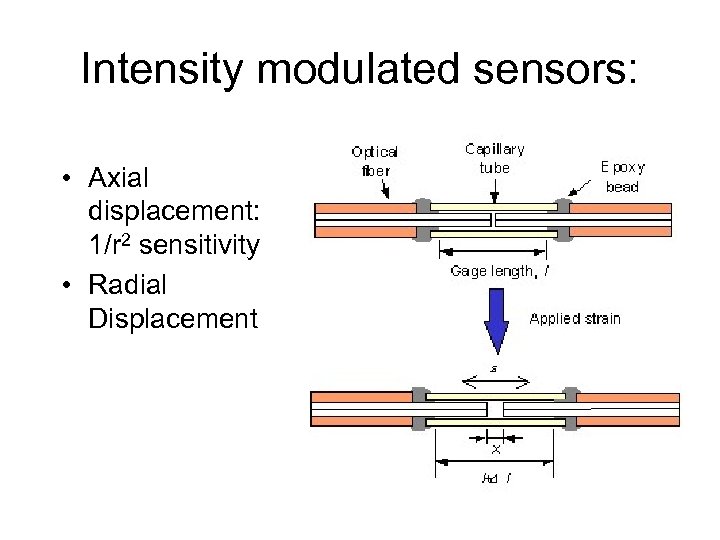 Intensity modulated sensors: • Axial displacement: 1/r 2 sensitivity • Radial Displacement
Intensity modulated sensors: • Axial displacement: 1/r 2 sensitivity • Radial Displacement
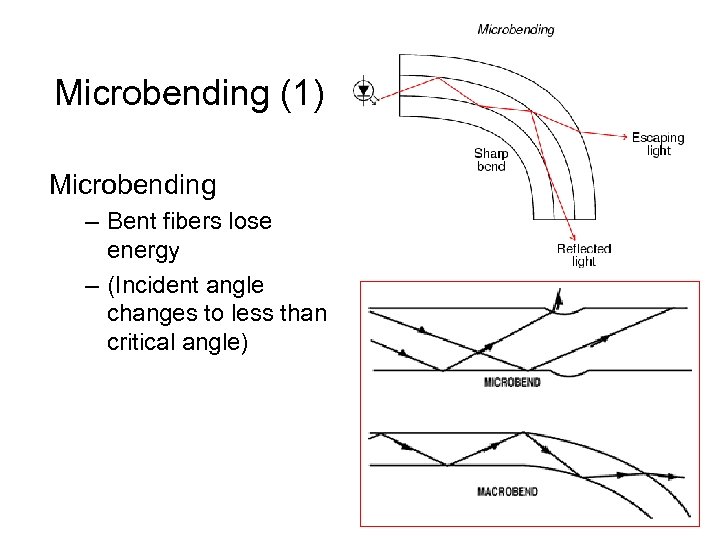 Microbending (1) Microbending – Bent fibers lose energy – (Incident angle changes to less than critical angle)
Microbending (1) Microbending – Bent fibers lose energy – (Incident angle changes to less than critical angle)
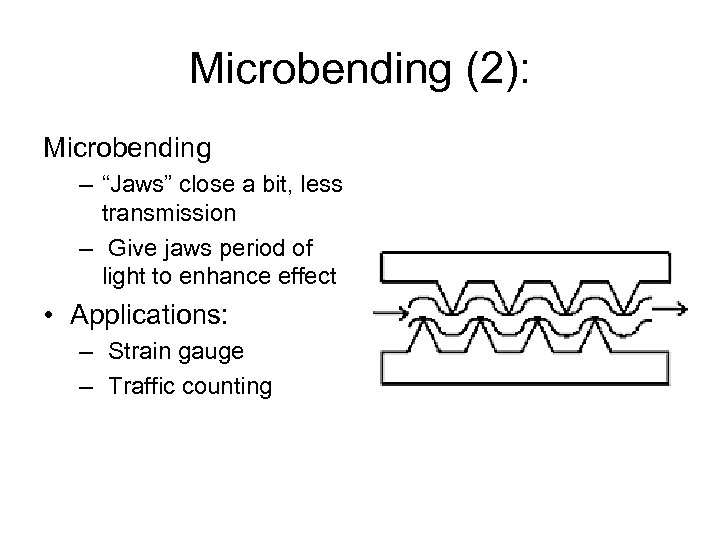 Microbending (2): Microbending – “Jaws” close a bit, less transmission – Give jaws period of light to enhance effect • Applications: – Strain gauge – Traffic counting
Microbending (2): Microbending – “Jaws” close a bit, less transmission – Give jaws period of light to enhance effect • Applications: – Strain gauge – Traffic counting
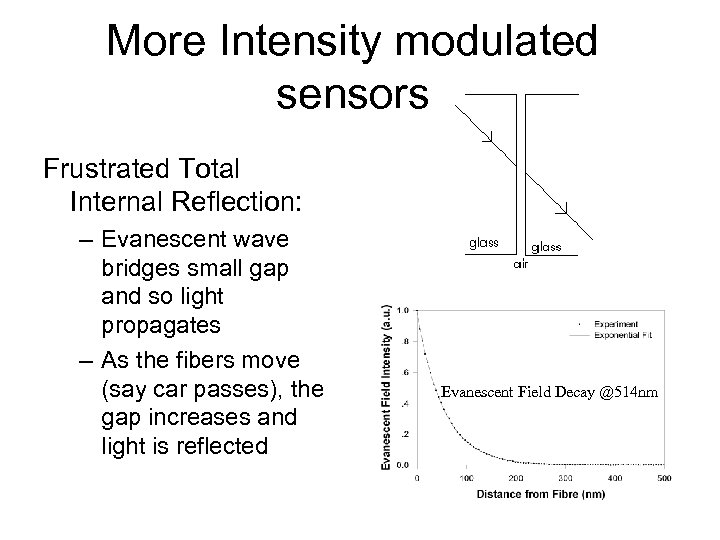 More Intensity modulated sensors Frustrated Total Internal Reflection: – Evanescent wave bridges small gap and so light propagates – As the fibers move (say car passes), the gap increases and light is reflected Evanescent Field Decay @514 nm
More Intensity modulated sensors Frustrated Total Internal Reflection: – Evanescent wave bridges small gap and so light propagates – As the fibers move (say car passes), the gap increases and light is reflected Evanescent Field Decay @514 nm
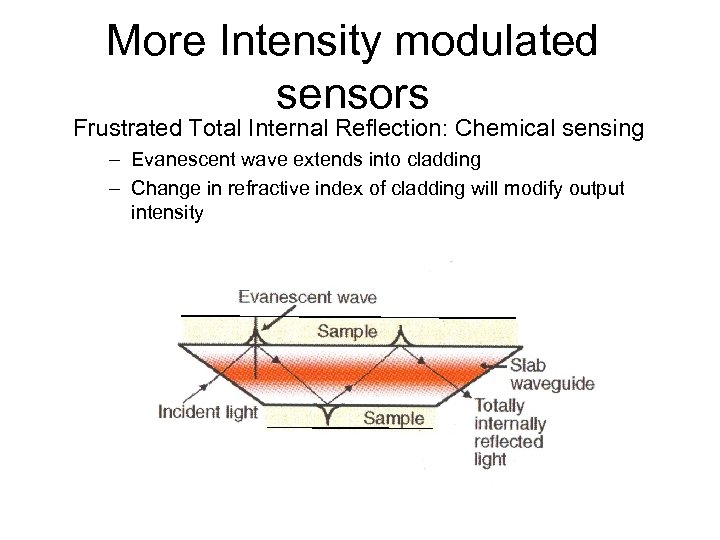 More Intensity modulated sensors Frustrated Total Internal Reflection: Chemical sensing – Evanescent wave extends into cladding – Change in refractive index of cladding will modify output intensity
More Intensity modulated sensors Frustrated Total Internal Reflection: Chemical sensing – Evanescent wave extends into cladding – Change in refractive index of cladding will modify output intensity
 Disadvantages of intensity modulated sensors • Light losses can be interpreted as change in measured property −Bends in fibres −Connecting fibres −Couplers • Variation in source power
Disadvantages of intensity modulated sensors • Light losses can be interpreted as change in measured property −Bends in fibres −Connecting fibres −Couplers • Variation in source power
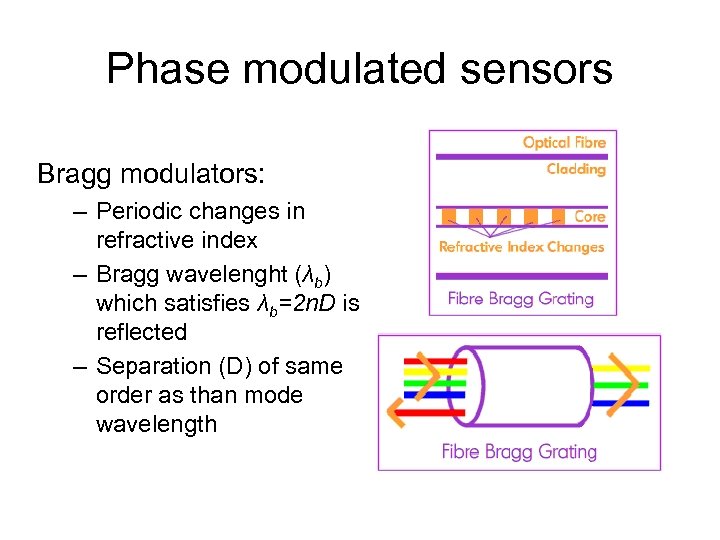 Phase modulated sensors Bragg modulators: – Periodic changes in refractive index – Bragg wavelenght (λb) which satisfies λb=2 n. D is reflected – Separation (D) of same order as than mode wavelength
Phase modulated sensors Bragg modulators: – Periodic changes in refractive index – Bragg wavelenght (λb) which satisfies λb=2 n. D is reflected – Separation (D) of same order as than mode wavelength
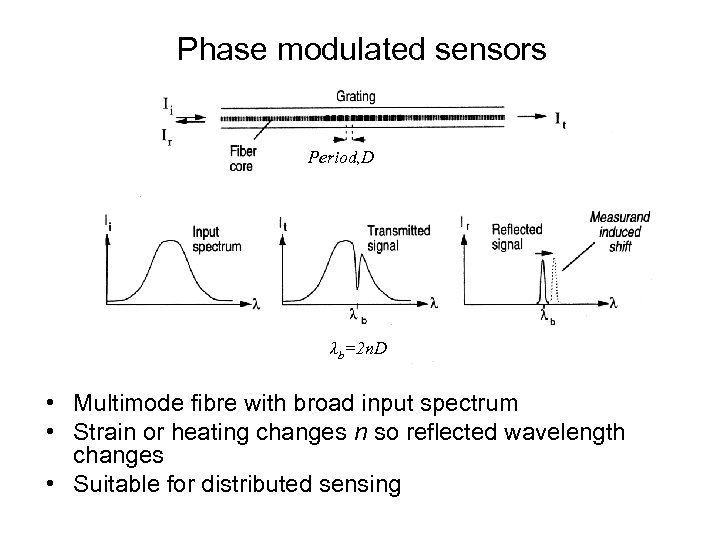 Phase modulated sensors Period, D λb=2 n. D • Multimode fibre with broad input spectrum • Strain or heating changes n so reflected wavelength changes • Suitable for distributed sensing
Phase modulated sensors Period, D λb=2 n. D • Multimode fibre with broad input spectrum • Strain or heating changes n so reflected wavelength changes • Suitable for distributed sensing
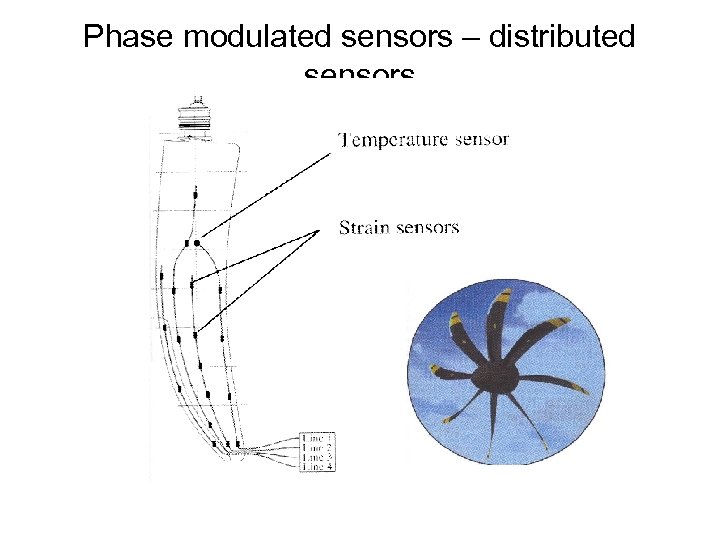 Phase modulated sensors – distributed sensors
Phase modulated sensors – distributed sensors
 Temperature Sensors • Reflected phosphorescent signal depends on Temperature • Can use BBR, but need sapphire waveguides since silica/glass absorbs IR
Temperature Sensors • Reflected phosphorescent signal depends on Temperature • Can use BBR, but need sapphire waveguides since silica/glass absorbs IR
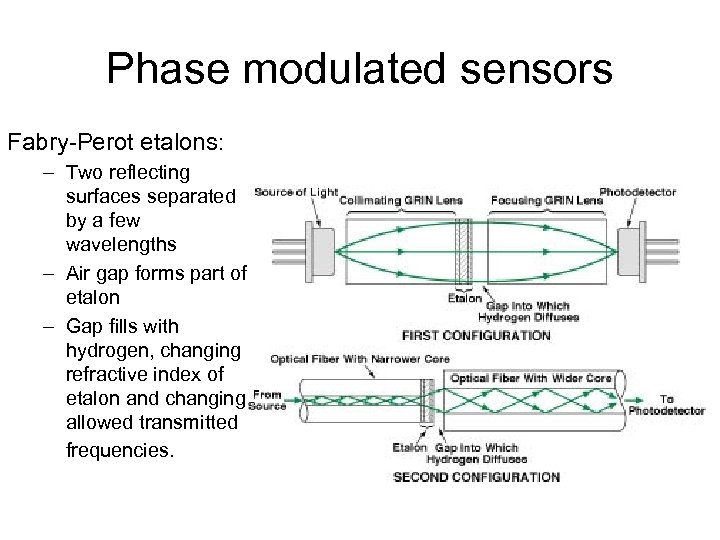 Phase modulated sensors Fabry-Perot etalons: – Two reflecting surfaces separated by a few wavelengths – Air gap forms part of etalon – Gap fills with hydrogen, changing refractive index of etalon and changing allowed transmitted frequencies.
Phase modulated sensors Fabry-Perot etalons: – Two reflecting surfaces separated by a few wavelengths – Air gap forms part of etalon – Gap fills with hydrogen, changing refractive index of etalon and changing allowed transmitted frequencies.
 Digital switches and counters • Measure number of air particles in air or water gap by drop in intensity – Environmental monitoring • Detect thin film thickness in manufacturing – Quality control • Counting things – Production line, traffic.
Digital switches and counters • Measure number of air particles in air or water gap by drop in intensity – Environmental monitoring • Detect thin film thickness in manufacturing – Quality control • Counting things – Production line, traffic.
 NSOM/AFM Combined • Optical resolution determined by diffraction limit (~λ) • Illuminating a sample with the "near-field" of a small light source. • Can construct optical images with resolution well beyond usual "diffraction limit", (typically ~50 nm. ) Bent NSOM/AFM Probe SEM - 70 nm aperture
NSOM/AFM Combined • Optical resolution determined by diffraction limit (~λ) • Illuminating a sample with the "near-field" of a small light source. • Can construct optical images with resolution well beyond usual "diffraction limit", (typically ~50 nm. ) Bent NSOM/AFM Probe SEM - 70 nm aperture
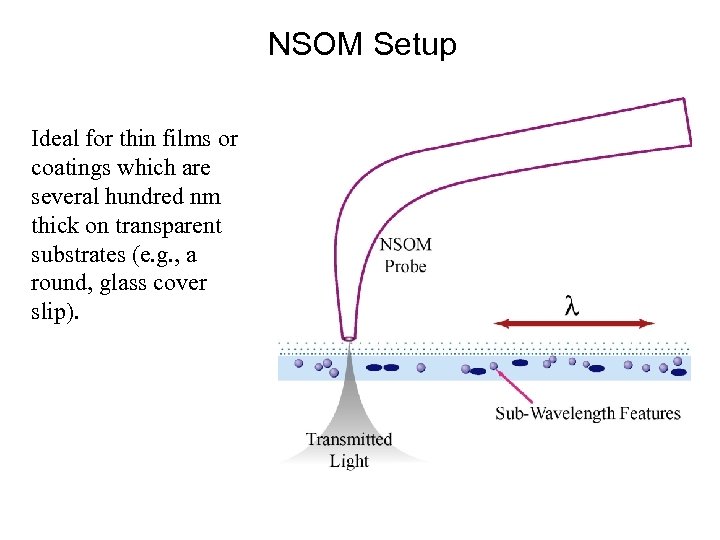 NSOM Setup Ideal for thin films or coatings which are several hundred nm thick on transparent substrates (e. g. , a round, glass cover slip).
NSOM Setup Ideal for thin films or coatings which are several hundred nm thick on transparent substrates (e. g. , a round, glass cover slip).
 Molecular Spectroscopy • Molecular Energy Levels – Vibrational Levels – Rotational levels • • Population of levels Intensities of transitions General features of spectroscopy An example: Raman Microscopy – Detection of art forgery – Local measurement of temperature
Molecular Spectroscopy • Molecular Energy Levels – Vibrational Levels – Rotational levels • • Population of levels Intensities of transitions General features of spectroscopy An example: Raman Microscopy – Detection of art forgery – Local measurement of temperature
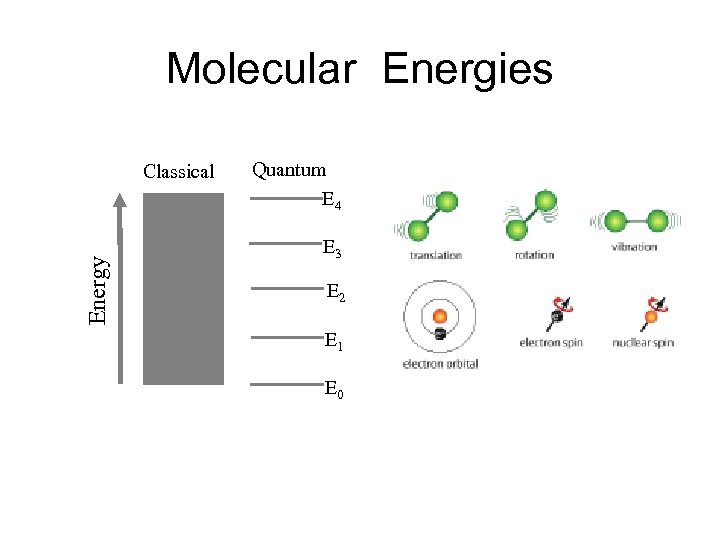 Molecular Energies Energy Classical Quantum E 4 E 3 E 2 E 1 E 0
Molecular Energies Energy Classical Quantum E 4 E 3 E 2 E 1 E 0
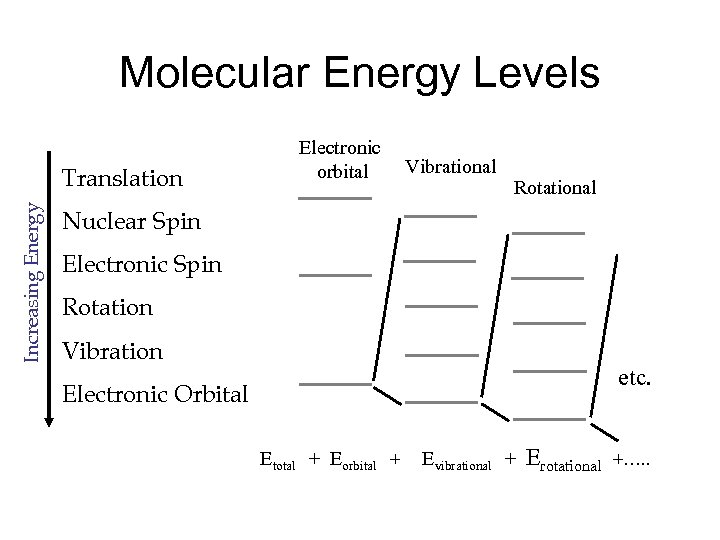 Molecular Energy Levels Increasing Energy Translation Electronic Vibrational orbital Rotational Nuclear Spin Electronic Spin Rotation Vibration Electronic Orbital etc. Etotal + Eorbital + Evibrational + Erotational +…. .
Molecular Energy Levels Increasing Energy Translation Electronic Vibrational orbital Rotational Nuclear Spin Electronic Spin Rotation Vibration Electronic Orbital etc. Etotal + Eorbital + Evibrational + Erotational +…. .
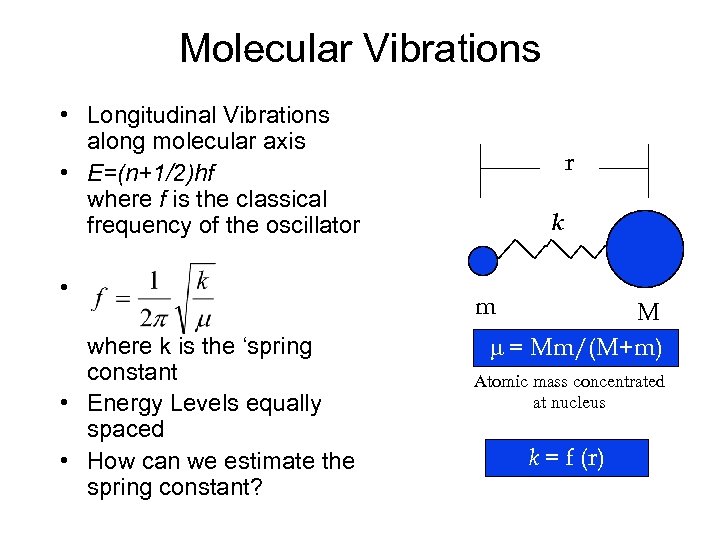 Molecular Vibrations • Longitudinal Vibrations along molecular axis • E=(n+1/2)hf where f is the classical frequency of the oscillator • where k is the ‘spring constant • Energy Levels equally spaced • How can we estimate the spring constant? r k m M = Mm/(M+m) Atomic mass concentrated at nucleus k = f (r)
Molecular Vibrations • Longitudinal Vibrations along molecular axis • E=(n+1/2)hf where f is the classical frequency of the oscillator • where k is the ‘spring constant • Energy Levels equally spaced • How can we estimate the spring constant? r k m M = Mm/(M+m) Atomic mass concentrated at nucleus k = f (r)
 Molecular Vibrations Hydrogen molecules, H 2, have ground state vibrational energy of 0. 273 e. V. Calculate force constant for the H 2 molecule (mass of H is 1. 008 amu) r • Evib=(n+1/2)hf f =0. 273 e. V/(1/2(h)) = 2. 07 x 1013 Hz K • To determine k we need μ μ=(Mm)/(M+m) =(1. 008)2/2(1. 008) amu m =(0. 504)1. 66 x 10 -27 kg =0. 837 x 10 -27 kg • k= μ(2πf)2 =576 N/m M = Mm/(M+m) K = f (r)
Molecular Vibrations Hydrogen molecules, H 2, have ground state vibrational energy of 0. 273 e. V. Calculate force constant for the H 2 molecule (mass of H is 1. 008 amu) r • Evib=(n+1/2)hf f =0. 273 e. V/(1/2(h)) = 2. 07 x 1013 Hz K • To determine k we need μ μ=(Mm)/(M+m) =(1. 008)2/2(1. 008) amu m =(0. 504)1. 66 x 10 -27 kg =0. 837 x 10 -27 kg • k= μ(2πf)2 =576 N/m M = Mm/(M+m) K = f (r)
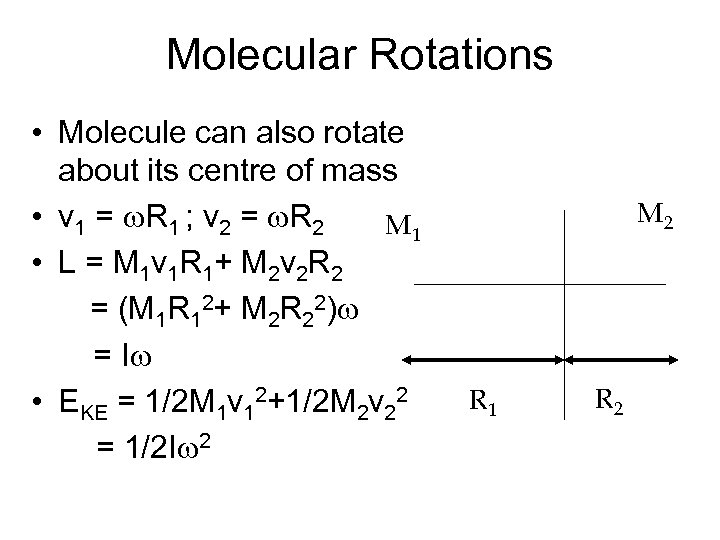 Molecular Rotations • Molecule can also rotate about its centre of mass • v 1 = w. R 1 ; v 2 = w. R 2 M 1 • L = M 1 v 1 R 1+ M 2 v 2 R 2 = (M 1 R 12+ M 2 R 22)w = Iw • EKE = 1/2 M 1 v 12+1/2 M 2 v 22 = 1/2 Iw 2 M 2 R 1 R 2
Molecular Rotations • Molecule can also rotate about its centre of mass • v 1 = w. R 1 ; v 2 = w. R 2 M 1 • L = M 1 v 1 R 1+ M 2 v 2 R 2 = (M 1 R 12+ M 2 R 22)w = Iw • EKE = 1/2 M 1 v 12+1/2 M 2 v 22 = 1/2 Iw 2 M 2 R 1 R 2
 Molecular Rotations • Hence, Erot= L 2/2 I • Now in fact L 2 is quantized and L 2=l(l+1)h 2/4 p 2 • Hence Erot=l(l+1)(h 2/4 p 2)/2 I • Show that DErot=(l+1) h 2/4 p 2/I. This is not equally spaced • Typically DErot=50 me. V (i. e for H 2)
Molecular Rotations • Hence, Erot= L 2/2 I • Now in fact L 2 is quantized and L 2=l(l+1)h 2/4 p 2 • Hence Erot=l(l+1)(h 2/4 p 2)/2 I • Show that DErot=(l+1) h 2/4 p 2/I. This is not equally spaced • Typically DErot=50 me. V (i. e for H 2)
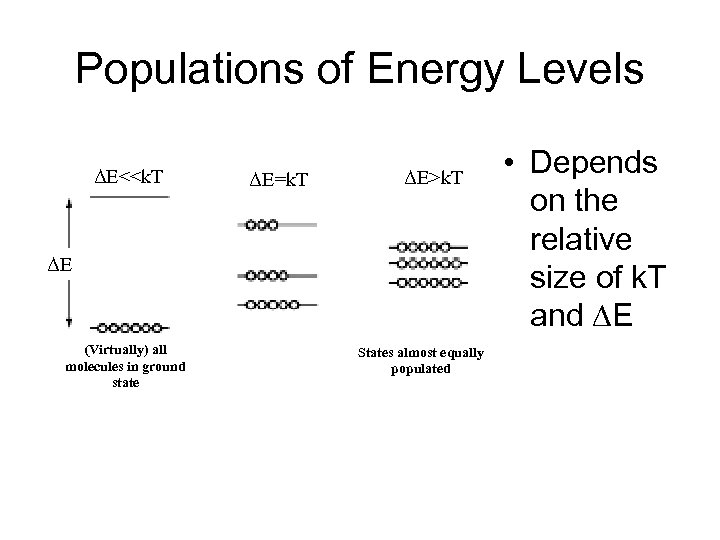 Populations of Energy Levels ΔE<
Populations of Energy Levels ΔE<
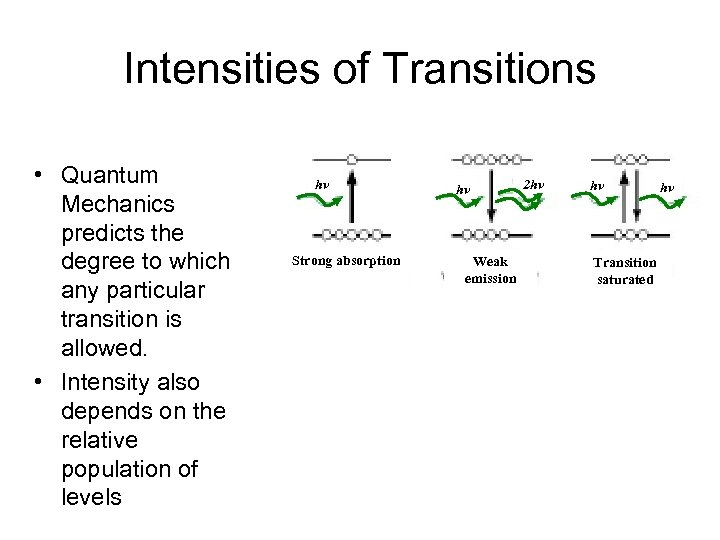 Intensities of Transitions • Quantum Mechanics predicts the degree to which any particular transition is allowed. • Intensity also depends on the relative population of levels hv Strong absorption hv Weak emission 2 hv hv Transition saturated hv
Intensities of Transitions • Quantum Mechanics predicts the degree to which any particular transition is allowed. • Intensity also depends on the relative population of levels hv Strong absorption hv Weak emission 2 hv hv Transition saturated hv
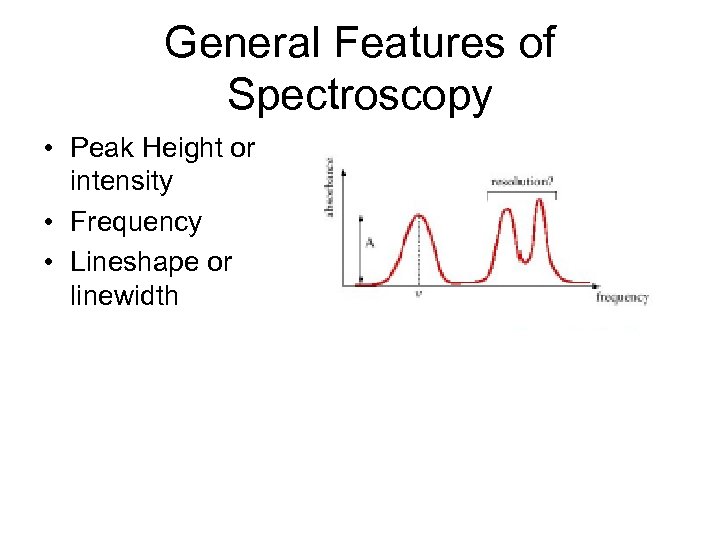 General Features of Spectroscopy • Peak Height or intensity • Frequency • Lineshape or linewidth
General Features of Spectroscopy • Peak Height or intensity • Frequency • Lineshape or linewidth
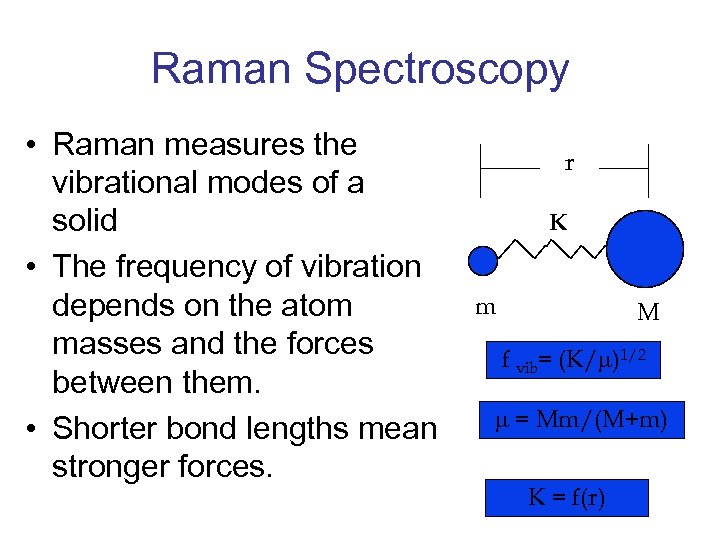 Raman Spectroscopy • Raman measures the vibrational modes of a solid • The frequency of vibration depends on the atom masses and the forces between them. • Shorter bond lengths mean stronger forces. r K m M f vib= (K/ )1/2 = Mm/(M+m) K = f(r)
Raman Spectroscopy • Raman measures the vibrational modes of a solid • The frequency of vibration depends on the atom masses and the forces between them. • Shorter bond lengths mean stronger forces. r K m M f vib= (K/ )1/2 = Mm/(M+m) K = f(r)
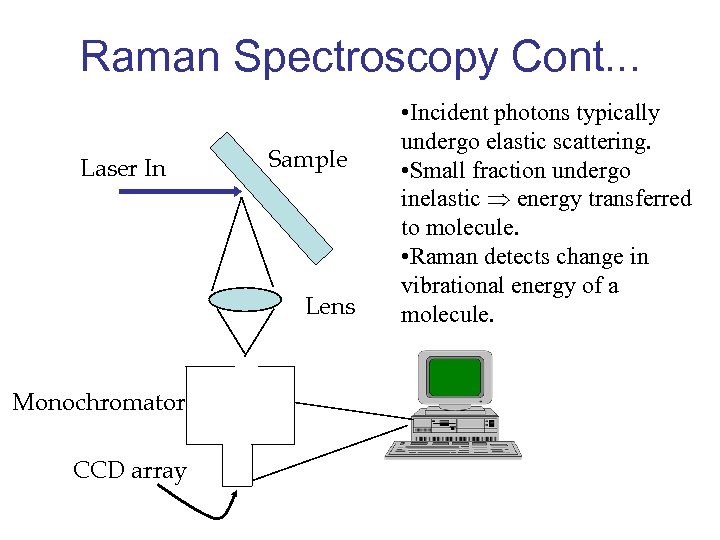 Raman Spectroscopy Cont. . . Laser In Sample Lens Monochromator CCD array • Incident photons typically undergo elastic scattering. • Small fraction undergo inelastic energy transferred to molecule. • Raman detects change in vibrational energy of a molecule.
Raman Spectroscopy Cont. . . Laser In Sample Lens Monochromator CCD array • Incident photons typically undergo elastic scattering. • Small fraction undergo inelastic energy transferred to molecule. • Raman detects change in vibrational energy of a molecule.
 Raman Microscope
Raman Microscope
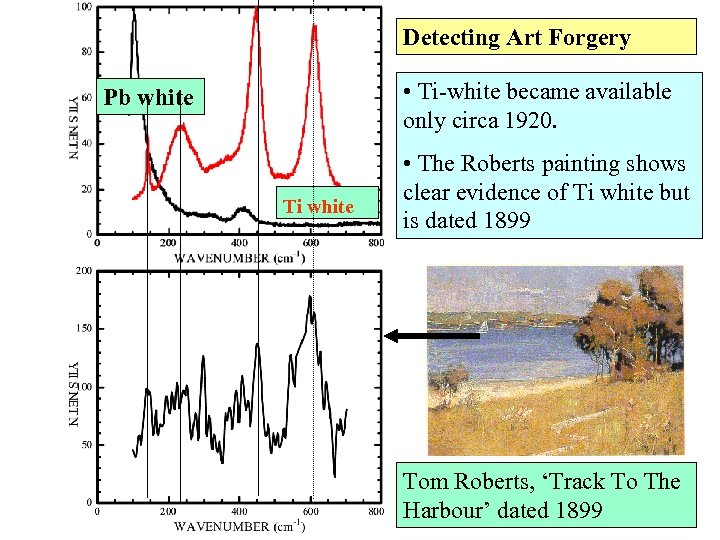 Detecting Art Forgery • Ti-white became available only circa 1920. Pb white Ti white • The Roberts painting shows clear evidence of Ti white but is dated 1899 Tom Roberts, ‘Track To The Harbour’ dated 1899
Detecting Art Forgery • Ti-white became available only circa 1920. Pb white Ti white • The Roberts painting shows clear evidence of Ti white but is dated 1899 Tom Roberts, ‘Track To The Harbour’ dated 1899
 Raman Spectroscopy and the Optical Measurement of Temperature • Probability that a level is occupied is proportional to exp(DE/k. T)
Raman Spectroscopy and the Optical Measurement of Temperature • Probability that a level is occupied is proportional to exp(DE/k. T)


