Photo credit Matthew Bannister, James Gibbs, and Charles d’Autremont Collective behavior of El Farol attendees European Conference on Complex Systems 2007 October 1 -6, 2007 – Dresden
Setting the stage A total number of N players must decide independently whether to attend the bar or not n n If a player forecasts that the total attendance will exceed the comfort level, L, she will not show up, otherwise she will go The attendance data of the last m weeks [am, am-1, …, a 1] are available to the agents n Each week we seek to find the number of people who will actually attend the bar, ao n WB Arthur Inductive Reasoning and Bounded Rationality American Economic Review 84, 406 (1994)
The algorithm pool n Point-wise hypothesis – the agent uses the attendance data of the kth previous week (1 ≤ k ≤ m) n Arithmetic average – the agent uses the average of the last k (1 < k ≤ m) weeks as her prediction Weighted average – the agent uses a weighted average of the last k (1 < k ≤ m) weeks, where the more recent a week’s data is, the larger weight it has n n Trend – the agent makes a least squares fit to the last k weeks’ data (1 < k ≤ m), and uses its extrapolation to the following week as her prediction Total of 4 m – 3 algorithms available, where m is the memory of the system
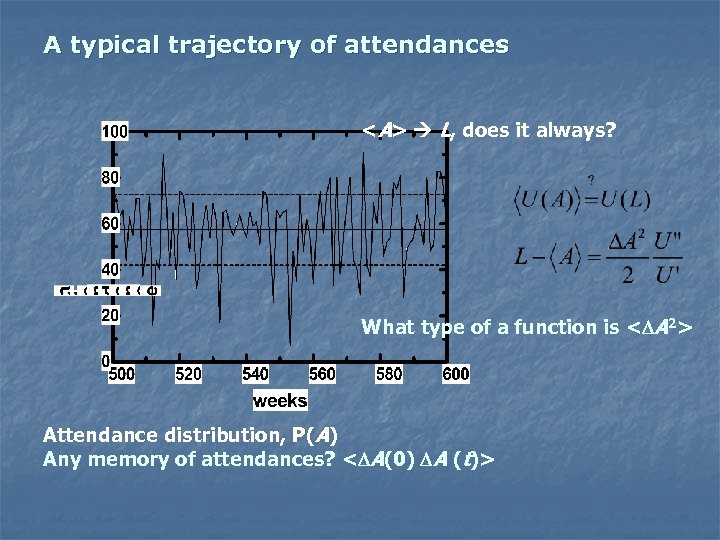
A typical trajectory of attendances <A> L, does it always? What type of a function is <DA 2> Attendance distribution, P(A) Any memory of attendances? <DA(0) DA (t)>
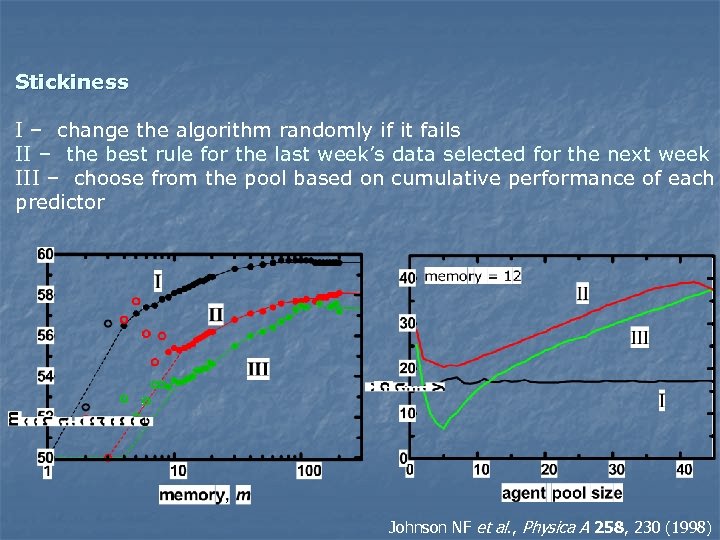
Stickiness I – change the algorithm randomly if it fails II – the best rule for the last week’s data selected for the next week III – choose from the pool based on cumulative performance of each predictor Johnson NF et al. , Physica A 258, 230 (1998)
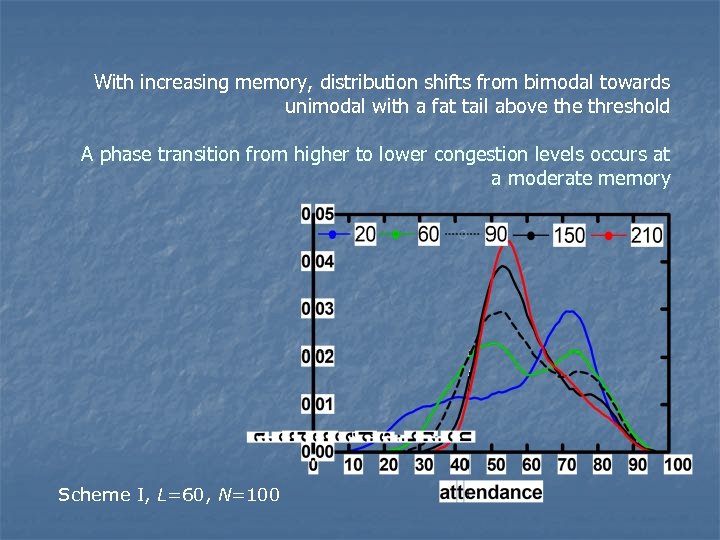
With increasing memory, distribution shifts from bimodal towards unimodal with a fat tail above threshold A phase transition from higher to lower congestion levels occurs at a moderate memory Scheme I, L=60, N=100
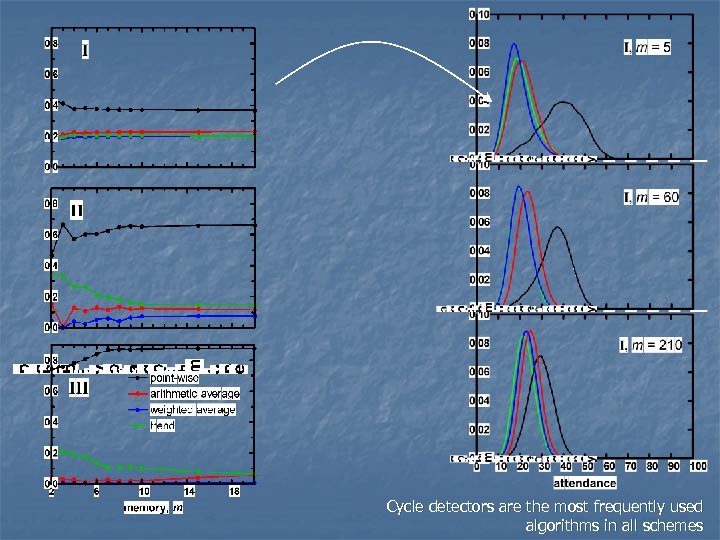
Cycle detectors are the most frequently used algorithms in all schemes
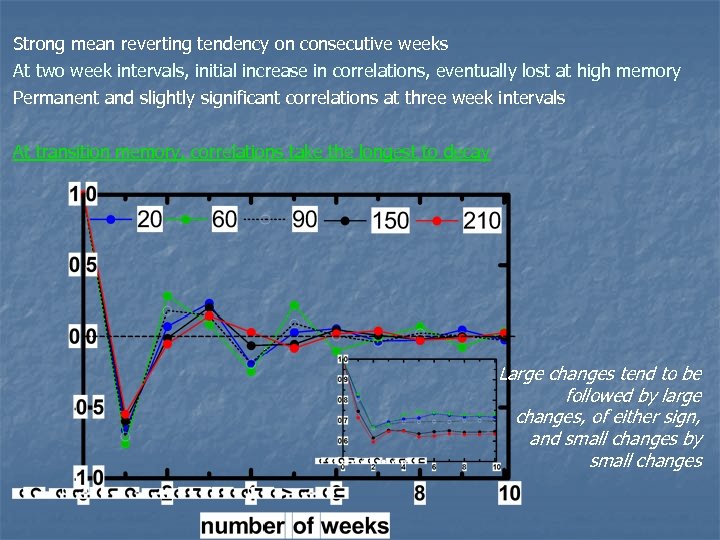
Strong mean reverting tendency on consecutive weeks At two week intervals, initial increase in correlations, eventually lost at high memory Permanent and slightly significant correlations at three week intervals At transition memory, correlations take the longest to decay Large changes tend to be followed by large changes, of either sign, and small changes by small changes
Agents’ confidence on their algorithms Convergence slightly affected Most significant shift during transition Correlations are accentuated and longer lasting only at transition memory
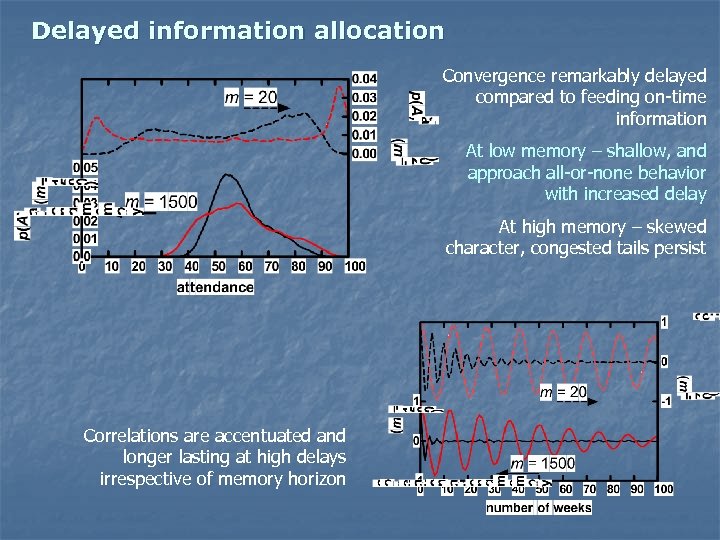
Delayed information allocation Convergence remarkably delayed compared to feeding on-time information At low memory – shallow, and approach all-or-none behavior with increased delay At high memory – skewed character, congested tails persist Correlations are accentuated and longer lasting at high delays irrespective of memory horizon
• Average attendance follows an S-shaped curve depending on the information carrying capacity • Whether the average attendance will converge externally provided comfort level or internally determined limiting state depends on the algorithm selection procedures • As critical memory is exceeded, algorithm usage probabilities are stabilized • The mean-reverting nature of the problem is also characterized by the correlations • A “phase transition” is observed as a function of information carrying capacity of the agents • Delaying information dissemination is more consequential than agents’ rigidity on their beliefs
Скачать презентацию Photo credit Matthew Bannister James Gibbs and Charles
54de7a87d203fb964c6afd9817e6e41b.ppt