Phonon Scattering Processes Affecting Thermal Conductance at Solid-solid

Phonon Scattering Processes Affecting Thermal Conductance at Solid-solid Interfaces in Nanomaterial Systems Patrick Hopkins University of Virginia Department of Mechanical and Aerospace Engineering March 10, 2008 Microscale Heat Transfer Lab – University of Virginia

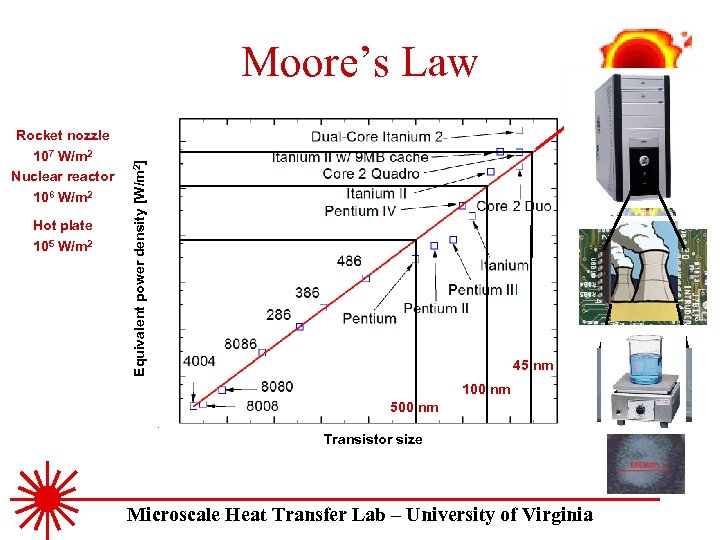Moore’s Law 107 W/m 2 Nuclear reactor 106 W/m 2 Hot plate 105 W/m 2 Equivalent power density [W/m 2] Rocket nozzle 45 nm 100 nm 500 nm Transistor size Microscale Heat Transfer Lab – University of Virginia

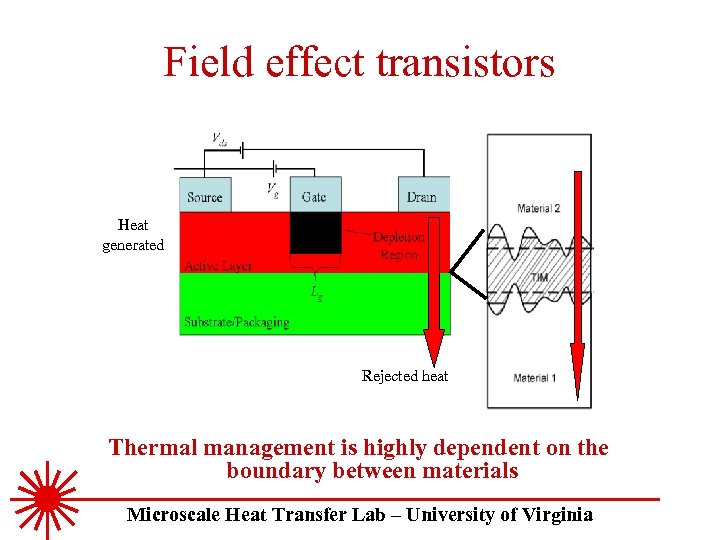Field effect transistors Heat generated Rejected heat Thermal management is highly dependent on the boundary between materials Microscale Heat Transfer Lab – University of Virginia

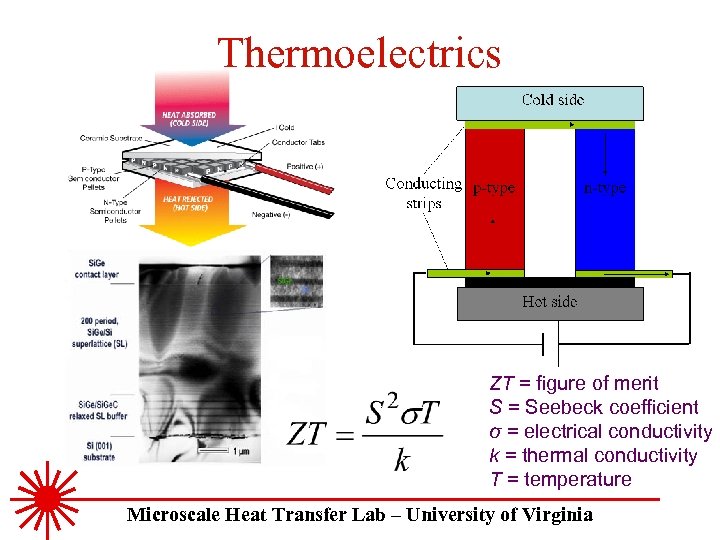Thermoelectrics ZT = figure of merit S = Seebeck coefficient σ = electrical conductivity k = thermal conductivity T = temperature Microscale Heat Transfer Lab – University of Virginia

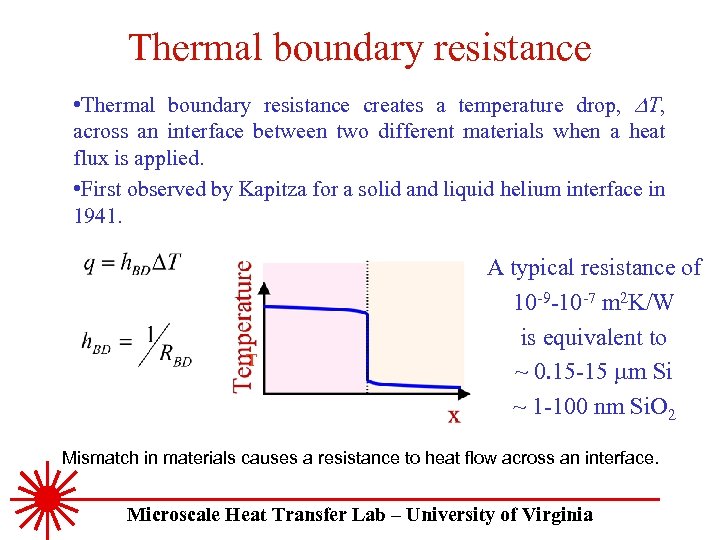Thermal boundary resistance • Thermal boundary resistance creates a temperature drop, DT, across an interface between two different materials when a heat flux is applied. • First observed by Kapitza for a solid and liquid helium interface in 1941. T A typical resistance of 10 -9 -10 -7 m 2 K/W is equivalent to ~ 0. 15 -15 mm Si ~ 1 -100 nm Si. O 2 Mismatch in materials causes a resistance to heat flow across an interface. Microscale Heat Transfer Lab – University of Virginia

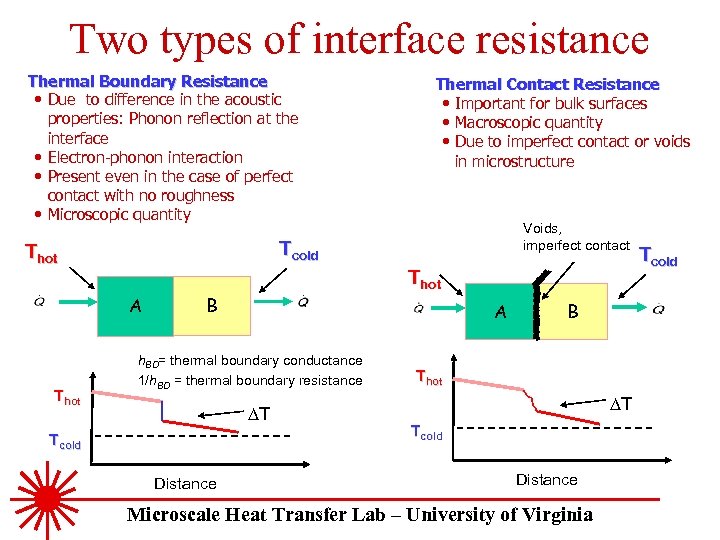Two types of interface resistance Thermal Boundary Resistance • Due to difference in the acoustic properties: Phonon reflection at the interface • Electron-phonon interaction • Present even in the case of perfect contact with no roughness • Microscopic quantity Voids, imperfect contact Tcold Thot A Thot Thermal Contact Resistance • Important for bulk surfaces • Macroscopic quantity • Due to imperfect contact or voids in microstructure B A h. BD= thermal boundary conductance 1/h. BD = thermal boundary resistance DT Tcold Distance B Thot DT Tcold Distance Microscale Heat Transfer Lab – University of Virginia Tcold

Major research objectives • the role of interface disorder on interfacial heat transfer • the effects of different phonon scattering mechanisms on interfacial heat transfer Microscale Heat Transfer Lab – University of Virginia

Outline of presentation • Theory of phonon interfacial transport • Measurement of interfacial transport with the transient thermoreflectance (TTR) technique • Influence of atomic mixing on interfacial phonon transport • Influence of high temperatures on interfacial phonon transport • Summary Microscale Heat Transfer Lab – University of Virginia

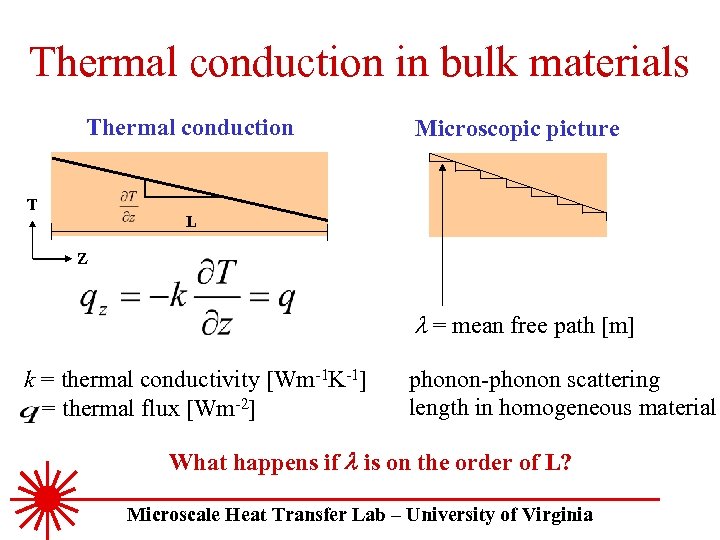Thermal conduction in bulk materials Thermal conduction T Microscopic picture L Z l = mean free path [m] k = thermal conductivity [Wm-1 K-1] = thermal flux [Wm-2] phonon-phonon scattering length in homogeneous material What happens if l is on the order of L? Microscale Heat Transfer Lab – University of Virginia

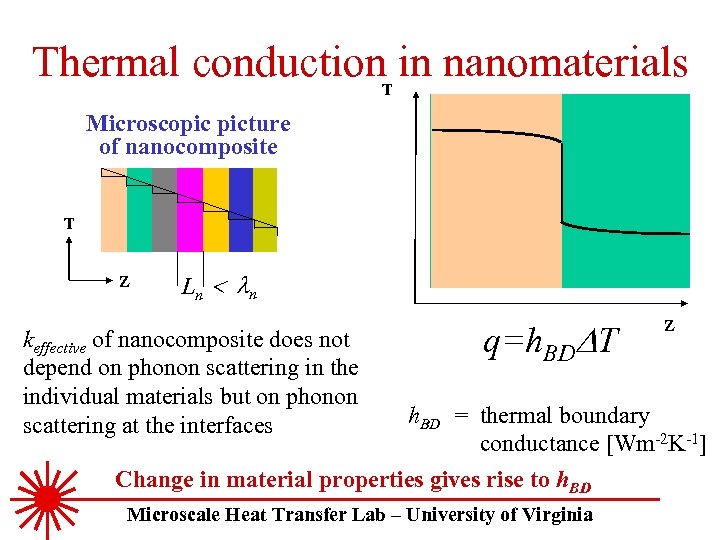Thermal conduction in nanomaterials T Microscopic picture of nanocomposite T Z Ln < l n keffective of nanocomposite does not depend on phonon scattering in the individual materials but on phonon scattering at the interfaces q=h. BDDT Z h. BD = thermal boundary conductance [Wm-2 K-1] Change in material properties gives rise to h. BD Microscale Heat Transfer Lab – University of Virginia

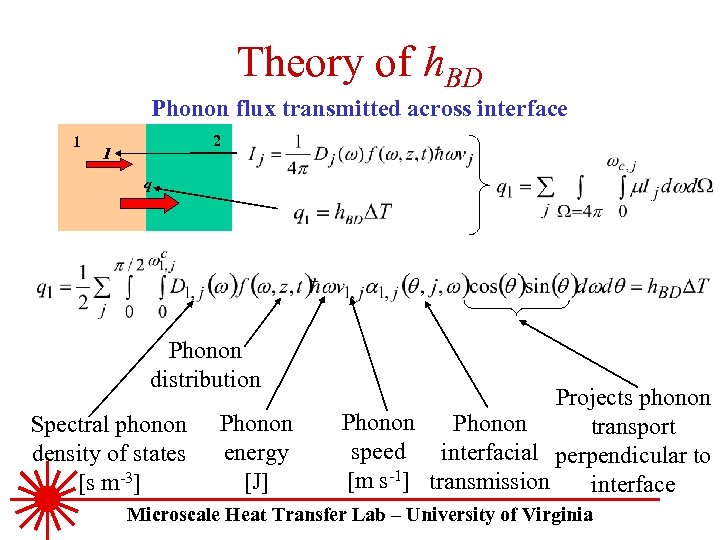Theory of h. BD Phonon flux transmitted across interface 1 2 I q Phonon distribution Spectral phonon density of states [s m-3] Phonon energy [J] Projects phonon Phonon transport speed interfacial perpendicular to [m s-1] transmission interface Microscale Heat Transfer Lab – University of Virginia

Diffuse scattering Diffuse Mismatch Model (DMM) E. T. Swartz and R. O. Pohl, 1989, "Thermal boundary resistance, ” Reviews of Modern Physics, 61, 605 -668. diffuse scattering – phonon “looses memory” when scattered • Scattering completely diffuse • Elastically isotropic materials • Single phonon elastic scattering T > 50 K and realistic interfaces Averaged properties in different crystallographic directions Is this assumption valid? Microscale Heat Transfer Lab – University of Virginia

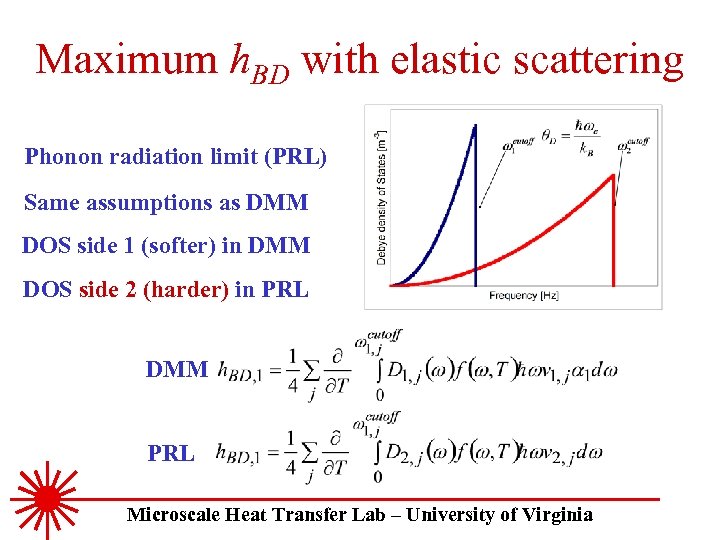Maximum h. BD with elastic scattering Phonon radiation limit (PRL) Same assumptions as DMM DOS side 1 (softer) in DMM DOS side 2 (harder) in PRL DMM PRL Microscale Heat Transfer Lab – University of Virginia

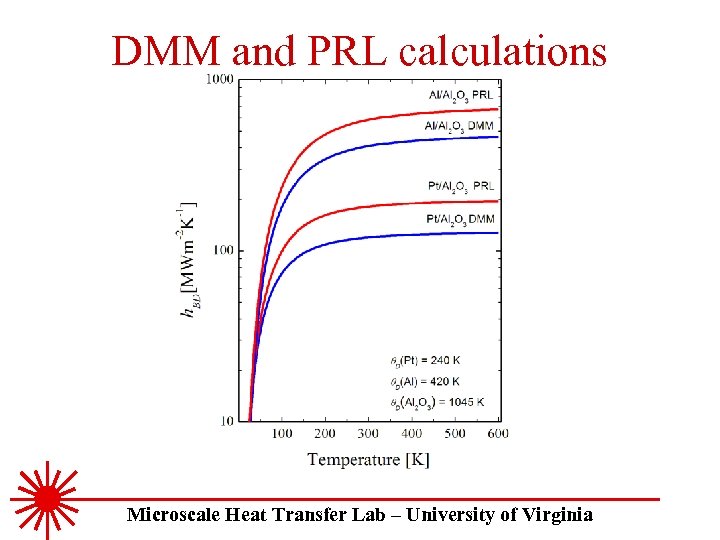DMM and PRL calculations Microscale Heat Transfer Lab – University of Virginia

Outline of presentation • Theory of phonon interfacial transport • Measurement of h. BD with the TTR technique • Influence of atomic mixing on h. BD • Influence of high temperatures (T > D) on h. BD • Summary Microscale Heat Transfer Lab – University of Virginia

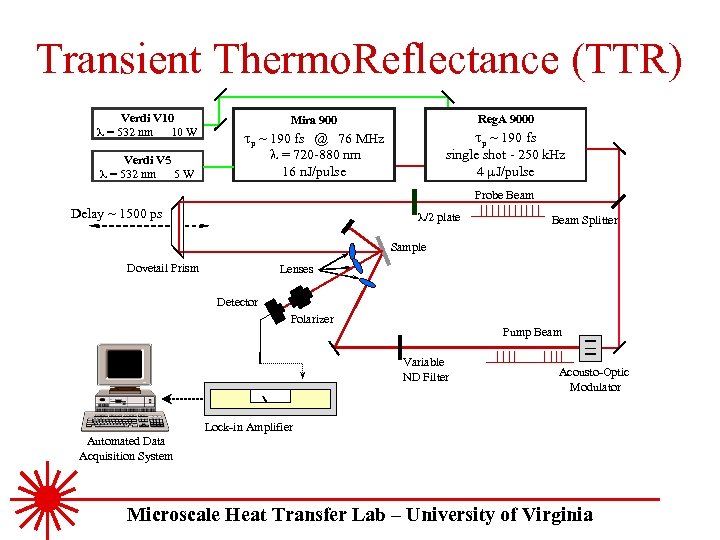Transient Thermo. Reflectance (TTR) Verdi V 10 = 532 nm 10 W Reg. A 9000 Mira 900 tp ~ 190 fs @ 76 MHz = 720 -880 nm 16 n. J/pulse Verdi V 5 = 532 nm 5 W single shot - 250 k. Hz 4 m. J/pulse Probe Beam Delay ~ 1500 ps /2 plate Beam Splitter Sample Dovetail Prism Lenses Detector Polarizer Pump Beam Variable ND Filter Acousto-Optic Modulator Lock-in Amplifier Automated Data Acquisition System Microscale Heat Transfer Lab – University of Virginia

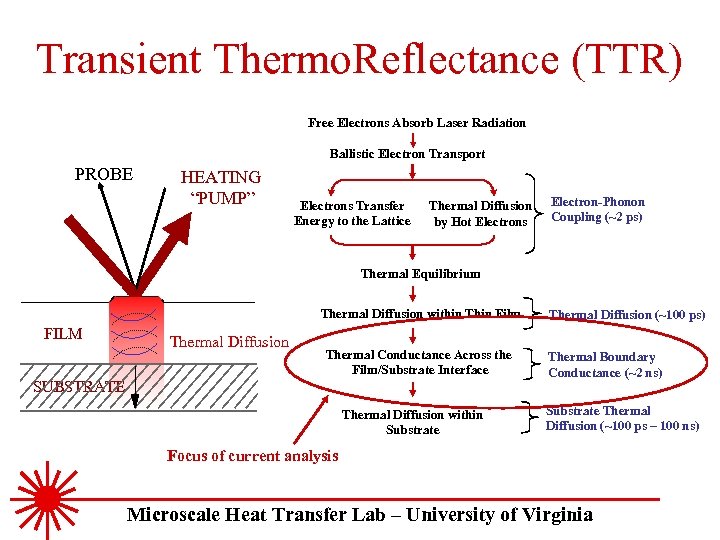Transient Thermo. Reflectance (TTR) Free Electrons Absorb Laser Radiation Ballistic Electron Transport PROBE HEATING “PUMP” Electrons Transfer Energy to the Lattice Thermal Diffusion by Hot Electrons Electron-Phonon Coupling (~2 ps) Thermal Equilibrium Thermal Diffusion within Thin Film FILM Thermal Diffusion Thermal Conductance Across the Film/Substrate Interface SUBSTRATE Thermal Diffusion within Substrate Thermal Diffusion (~100 ps) Thermal Boundary Conductance (~2 ns) Substrate Thermal Diffusion (~100 ps – 100 ns) Focus of current analysis Microscale Heat Transfer Lab – University of Virginia

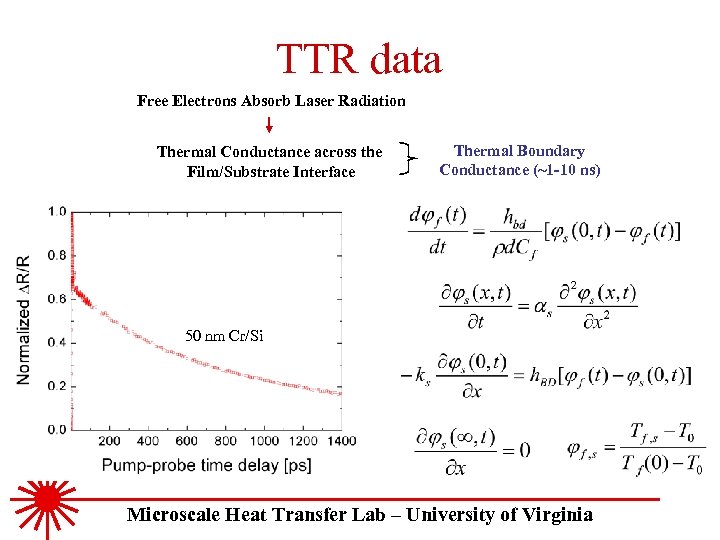TTR data Free Electrons Absorb Laser Radiation Thermal Conductance across the Film/Substrate Interface Thermal Boundary Conductance (~1 -10 ns) 50 nm Cr/Si Microscale Heat Transfer Lab – University of Virginia

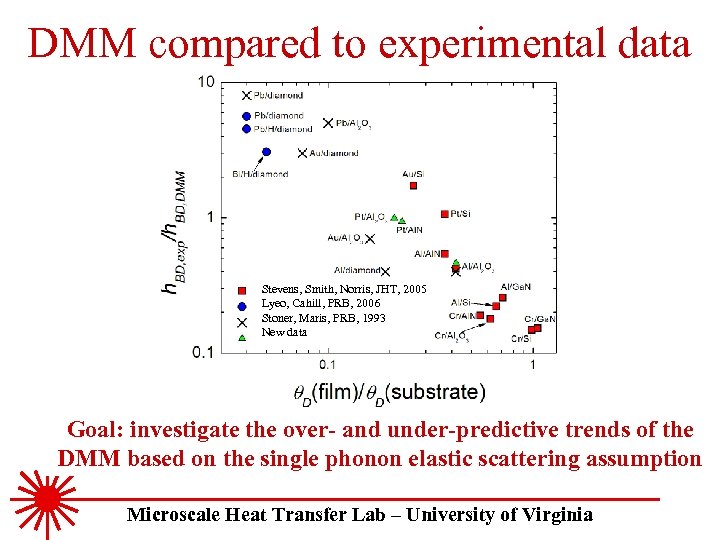DMM compared to experimental data Stevens, Smith, Norris, JHT, 2005 Lyeo, Cahill, PRB, 2006 Stoner, Maris, PRB, 1993 New data Goal: investigate the over- and under-predictive trends of the DMM based on the single phonon elastic scattering assumption Microscale Heat Transfer Lab – University of Virginia

Outline of presentation • Theory of phonon interfacial transport • Measurement of h. BD with the TTR technique • Influence of atomic mixing on h. BD • Influence of high temperatures (T > D) on h. BD • Summary Microscale Heat Transfer Lab – University of Virginia

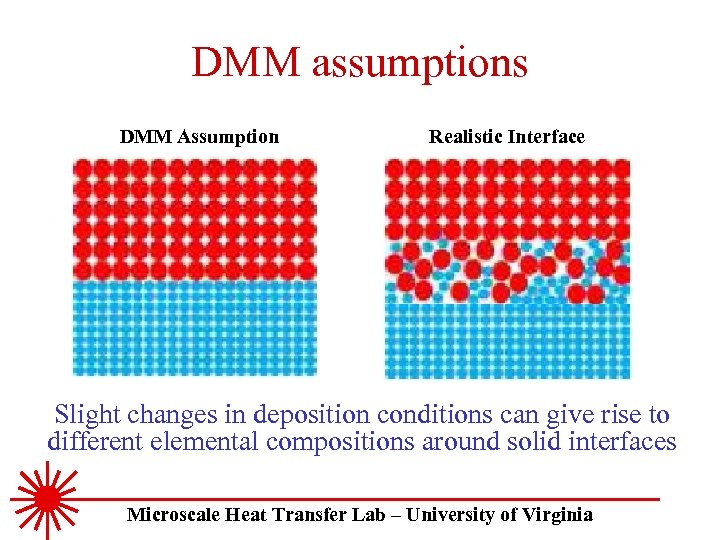DMM assumptions DMM Assumption Realistic Interface Slight changes in deposition conditions can give rise to different elemental compositions around solid interfaces Microscale Heat Transfer Lab – University of Virginia

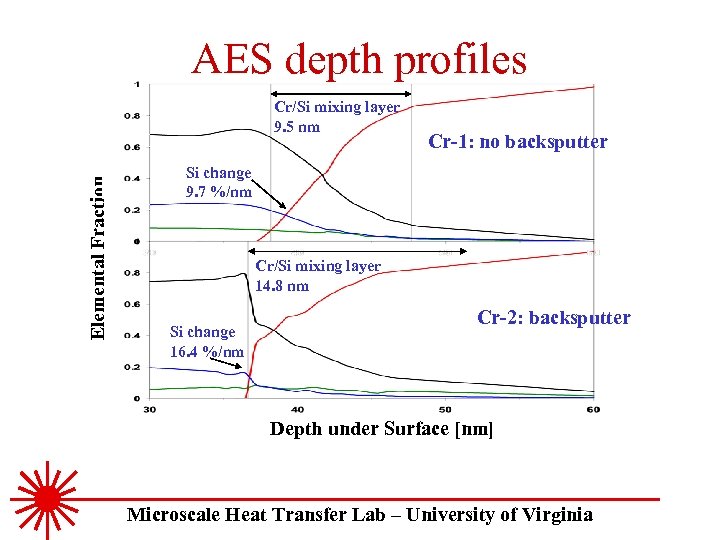AES depth profiles Elemental Fraction Cr/Si mixing layer 9. 5 nm Cr-1: no backsputter Si change 9. 7 %/nm Cr/Si mixing layer 14. 8 nm Si change 16. 4 %/nm Cr-2: backsputter Depth under Surface [nm] Microscale Heat Transfer Lab – University of Virginia

Results from AES data Sample ID Mixing Layer [nm] Cr-1 Cr Film Thickness [nm] 38 ± 2. 1 9. 5 ± 0. 6 Slope of Si in Beginning of Mixing Layer [%/nm] 9. 7 ± 0. 7 Cr-2 Cr-3 Cr-4 Cr-5 Cr-6 37 ± 0. 4 35 ± 0. 5 35 ± 2. 8 39 ± 0. 5 45 ± 0. 5 14. 8 ± 1. 0 11. 5 ± 0. 7 10. 8 ± 0. 8 5. 8 ± 0. 5 7. 0 ± 0. 4 16. 4 ± 0. 7 16. 6 ± 1. 0 7. 4 ± 1. 0 24. 1 ± 1. 0 28. 1 ± 1. 2 Microscale Heat Transfer Lab – University of Virginia

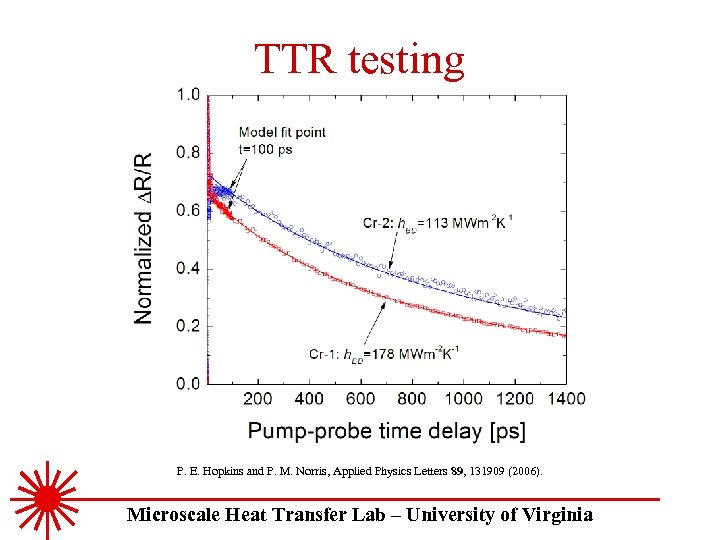TTR testing P. E. Hopkins and P. M. Norris, Applied Physics Letters 89, 131909 (2006). Microscale Heat Transfer Lab – University of Virginia

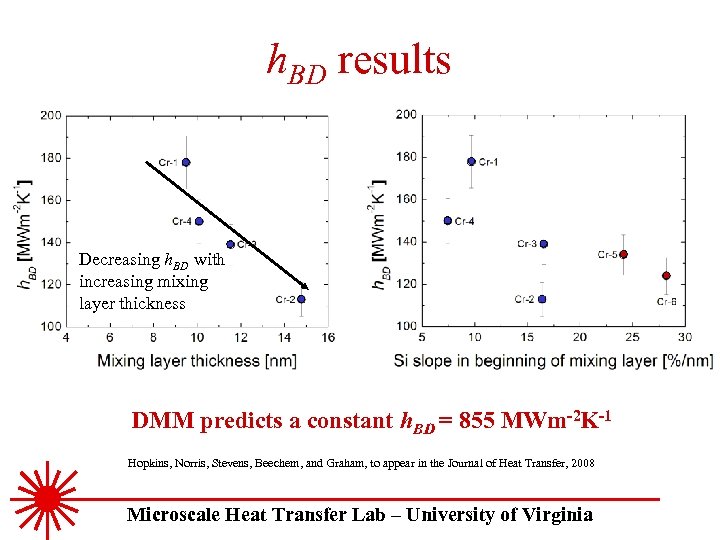h. BD results Decreasing h. BD with increasing mixing layer thickness DMM predicts a constant h. BD = 855 MWm-2 K-1 Hopkins, Norris, Stevens, Beechem, and Graham, to appear in the Journal of Heat Transfer, 2008 Microscale Heat Transfer Lab – University of Virginia

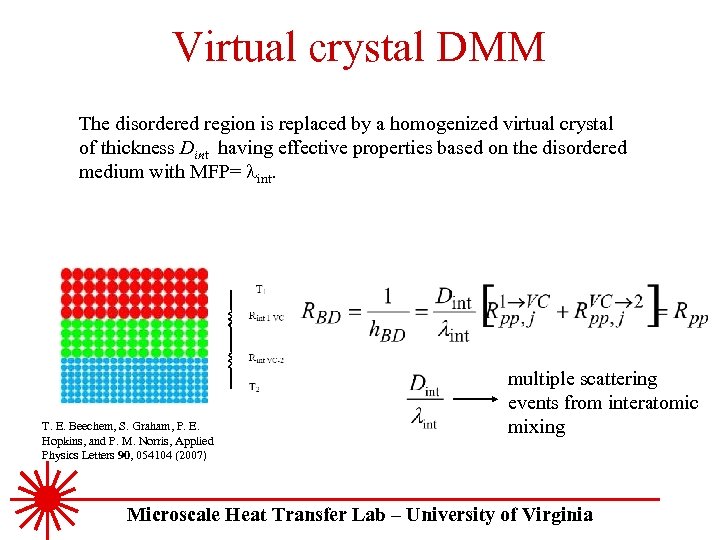Virtual crystal DMM The disordered region is replaced by a homogenized virtual crystal of thickness Dint having effective properties based on the disordered medium with MFP= int. T. E. Beechem, S. Graham, P. E. Hopkins, and P. M. Norris, Applied Physics Letters 90, 054104 (2007) multiple scattering events from interatomic mixing Microscale Heat Transfer Lab – University of Virginia

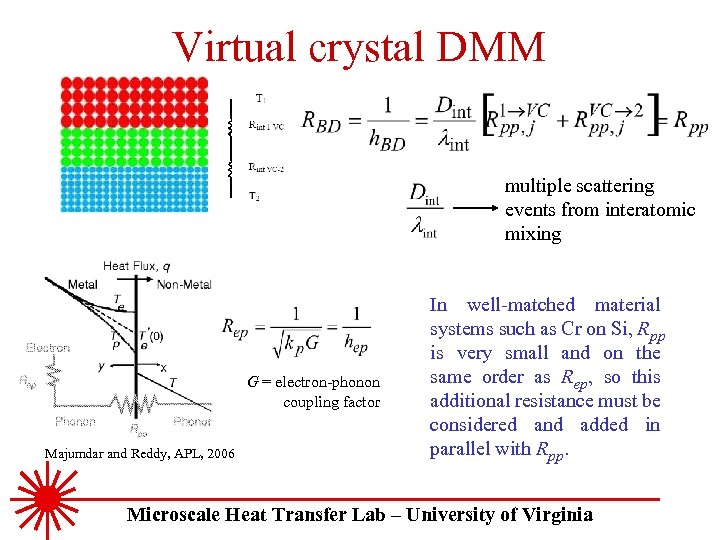Virtual crystal DMM multiple scattering events from interatomic mixing G = electron-phonon coupling factor Majumdar and Reddy, APL, 2006 In well-matched material systems such as Cr on Si, Rpp is very small and on the same order as Rep, so this additional resistance must be considered and added in parallel with Rpp. Microscale Heat Transfer Lab – University of Virginia

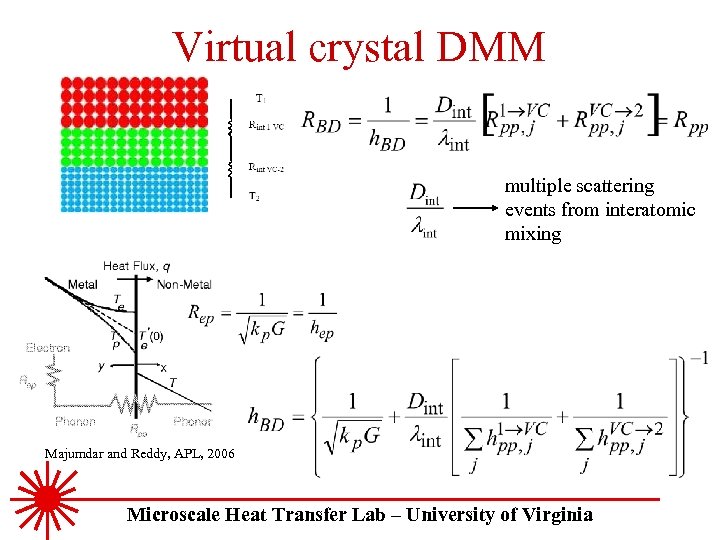Virtual crystal DMM multiple scattering events from interatomic mixing Majumdar and Reddy, APL, 2006 Microscale Heat Transfer Lab – University of Virginia

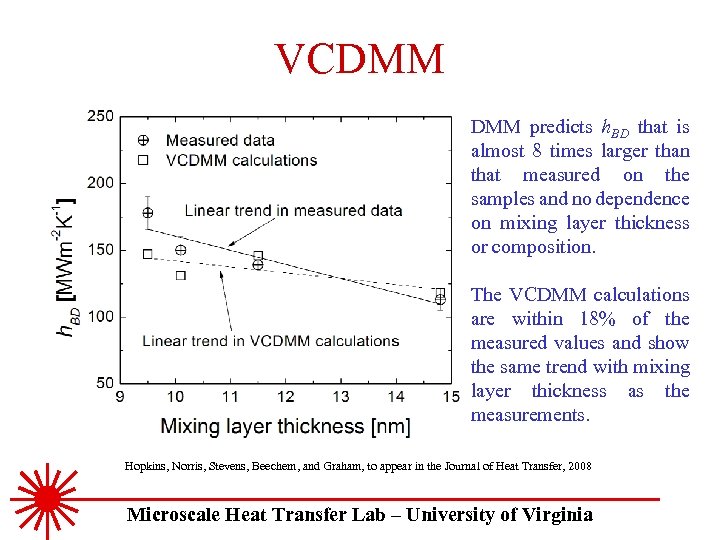VCDMM predicts h. BD that is almost 8 times larger than that measured on the samples and no dependence on mixing layer thickness or composition. The VCDMM calculations are within 18% of the measured values and show the same trend with mixing layer thickness as the measurements. Hopkins, Norris, Stevens, Beechem, and Graham, to appear in the Journal of Heat Transfer, 2008 Microscale Heat Transfer Lab – University of Virginia

Summary Investigate the role of interface disorder on interfacial heat transfer • Examined the effects of interfacial properties on h. BD in the acoustically matched Cr/Si system with TTR • DMM predicts h. BD 855 MWm-2 K-1 at room temperature • Measured data varies from 100 -200 MWm-2 K-1, depending on deposition conditions • Multiple phonon elastic scattering could cause this overprediction of the DMM • DMM only takes into account single scattering events • DMM assumes a perfect interface, but interface disorder will increase the scattering thus decreasing the h. BD • VCDMM is introduced and predicts same values and trends for Cr/Si at room temperature as experimental data Microscale Heat Transfer Lab – University of Virginia

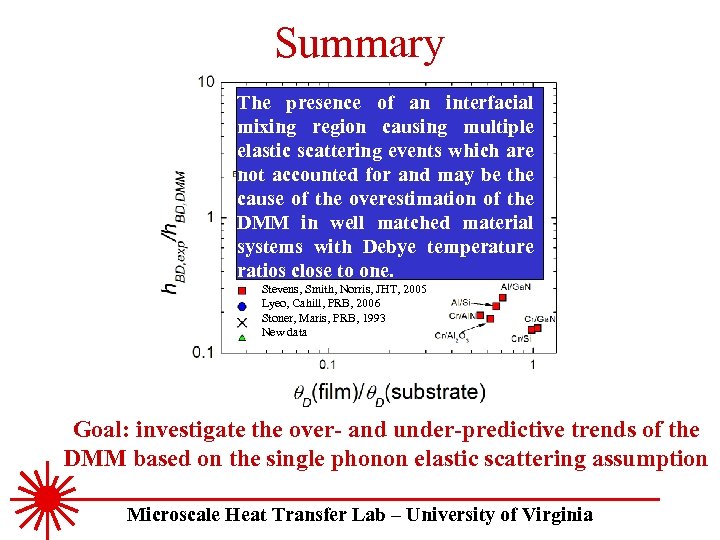Summary The presence of an interfacial mixing region causing multiple elastic scattering events which are not accounted for and may be the cause of the overestimation of the DMM in well matched material systems with Debye temperature ratios close to one. Stevens, Smith, Norris, JHT, 2005 Lyeo, Cahill, PRB, 2006 Stoner, Maris, PRB, 1993 New data Goal: investigate the over- and under-predictive trends of the DMM based on the single phonon elastic scattering assumption Microscale Heat Transfer Lab – University of Virginia

Outline of presentation • Theory of phonon interfacial transport • Measurement of h. BD with the TTR technique • Influence of atomic mixing on h. BD • Influence of high temperatures (T > D) on h. BD • Summary Microscale Heat Transfer Lab – University of Virginia

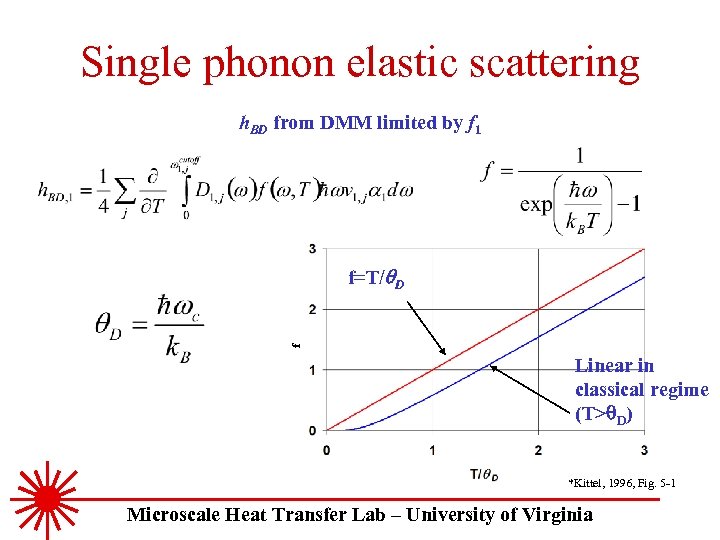Single phonon elastic scattering h. BD from DMM limited by f 1 f f=T/ D Linear in classical regime (T>q. D) *Kittel, 1996, Fig. 5 -1 Microscale Heat Transfer Lab – University of Virginia

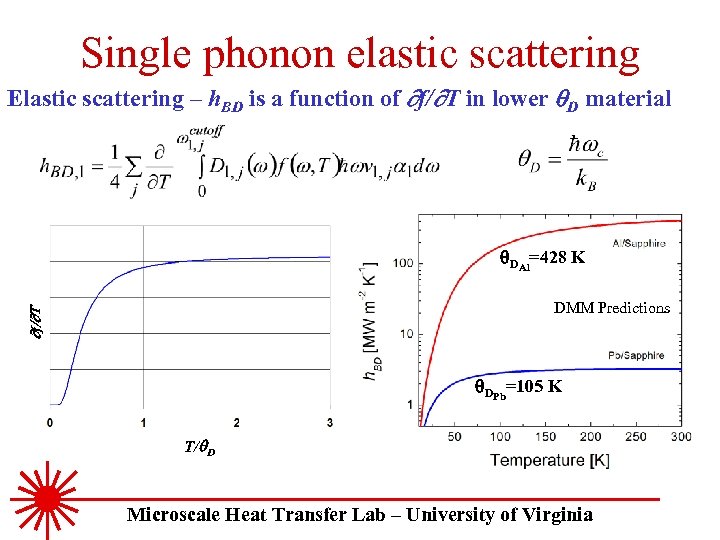Single phonon elastic scattering Elastic scattering – h. BD is a function of f/ T in lower D material q. DAl=428 K f DMM Predictions q. DPb=105 K T/ D Microscale Heat Transfer Lab – University of Virginia

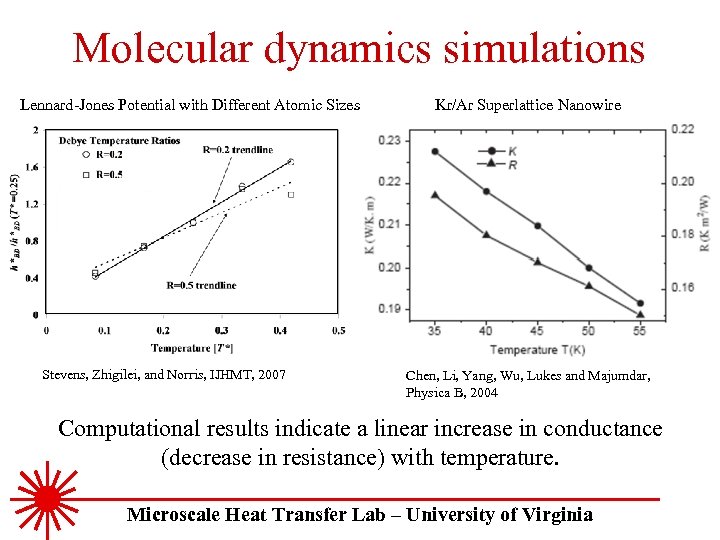Molecular dynamics simulations Lennard-Jones Potential with Different Atomic Sizes Stevens, Zhigilei, and Norris, IJHMT, 2007 Kr/Ar Superlattice Nanowire Chen, Li, Yang, Wu, Lukes and Majumdar, Physica B, 2004 Computational results indicate a linear increase in conductance (decrease in resistance) with temperature. Microscale Heat Transfer Lab – University of Virginia

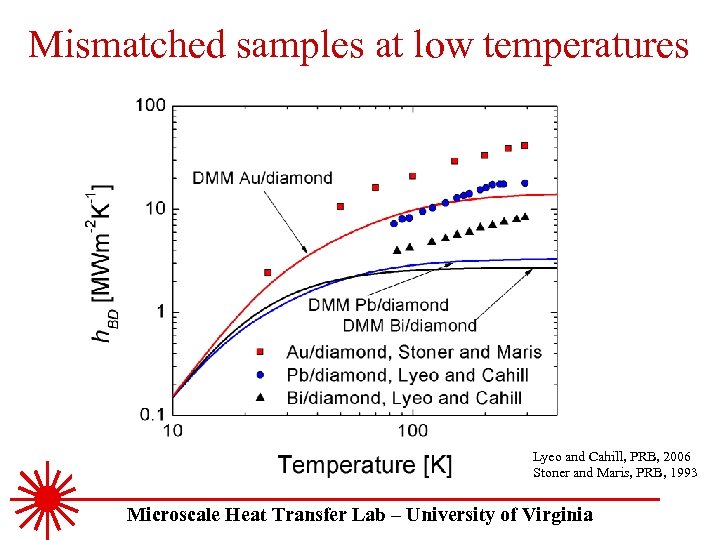Mismatched samples at low temperatures Lyeo and Cahill, PRB, 2006 Stoner and Maris, PRB, 1993 Microscale Heat Transfer Lab – University of Virginia

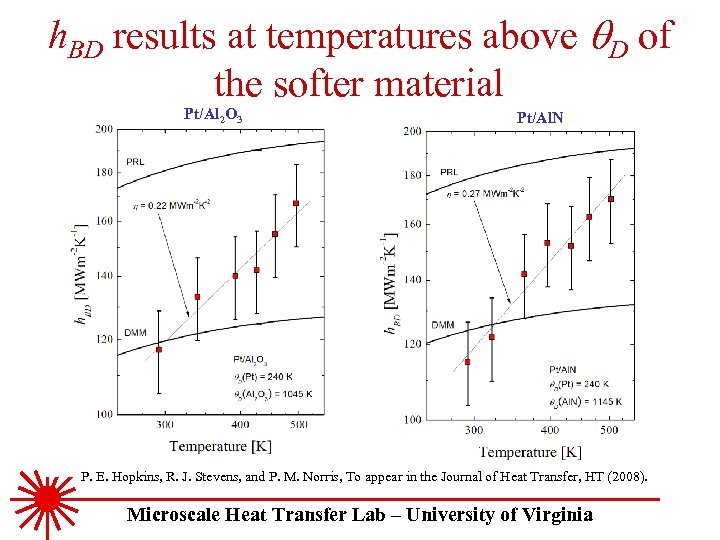h. BD results at temperatures above q. D of the softer material Pt/Al 2 O 3 Pt/Al. N P. E. Hopkins, R. J. Stevens, and P. M. Norris, To appear in the Journal of Heat Transfer, HT (2008). Microscale Heat Transfer Lab – University of Virginia

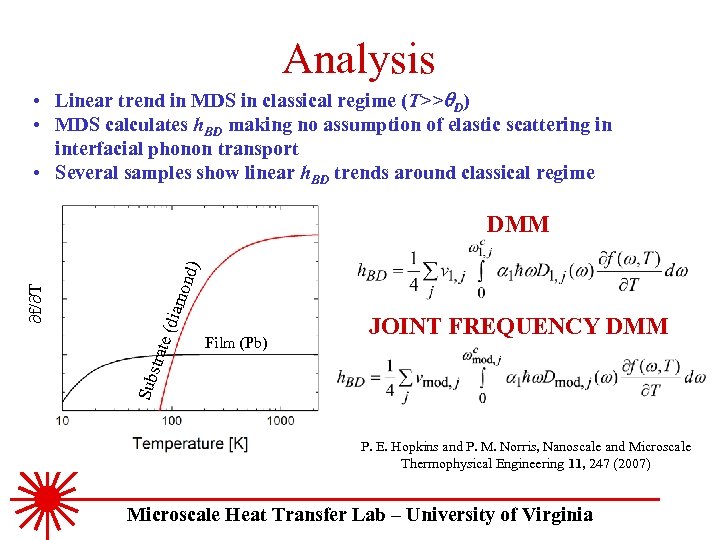Analysis • Linear trend in MDS in classical regime (T>> D) • MDS calculates h. BD making no assumption of elastic scattering in interfacial phonon transport • Several samples show linear h. BD trends around classical regime ond rate (dia m Film (Pb) JOINT FREQUENCY DMM Sub st f/ T ) DMM P. E. Hopkins and P. M. Norris, Nanoscale and Microscale Thermophysical Engineering 11, 247 (2007) Microscale Heat Transfer Lab – University of Virginia

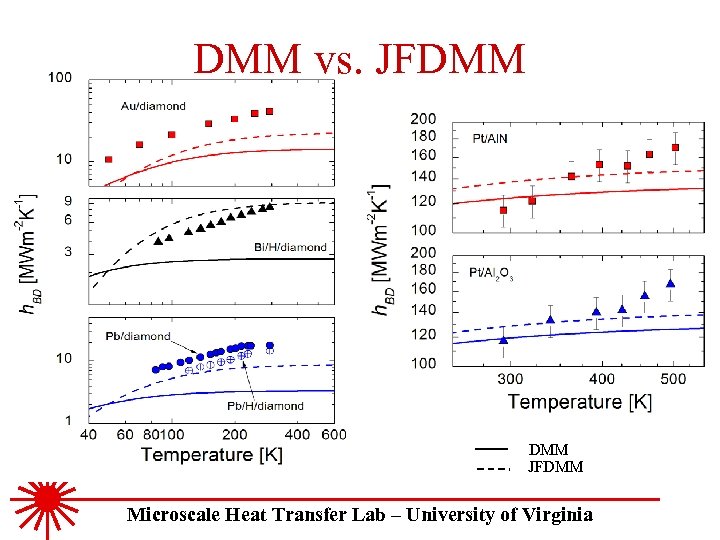DMM vs. JFDMM Microscale Heat Transfer Lab – University of Virginia

Summary Investigate the effects of different phonon scattering mechanisms on interfacial heat transfer • Measured h. BD at different metal-dielectric interfaces with a range of acoustic similarity • Observed linear trend in h. BD around D • Evidence of inelastic scattering – not predicted with DMM • JFDMM takes into account substrate phonons – and provides better agreement with experimental data Microscale Heat Transfer Lab – University of Virginia

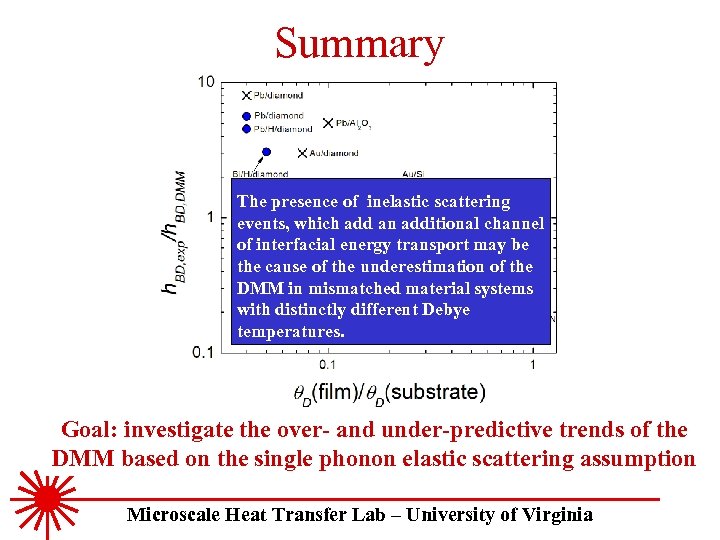Summary The presence of inelastic scattering events, which add an additional channel of interfacial energy transport may be the cause of the underestimation of the Stevens, mismatched material systems DMM in Smith, Norris, JHT, 2005 Lyeo, Cahill, PRB, 2006 with distinctly different Debye Stoner, Maris, PRB, 1993 New data temperatures. Goal: investigate the over- and under-predictive trends of the DMM based on the single phonon elastic scattering assumption Microscale Heat Transfer Lab – University of Virginia

Outline of presentation • Theory of phonon interfacial transport • Measurement of h. BD with the TTR technique • Influence of atomic mixing on h. BD • Influence of high temperatures (T > D) on h. BD • Summary Microscale Heat Transfer Lab – University of Virginia

Conclusions Investigate the role of interface disorder on interfacial heat transfer • Determined that interfacial mixing can play a role in phonon transport by inducing multiple phonon scattering events • Accurately described with VCDMM taking into account e-p resistance Investigate the effects of different phonon scattering mechanisms on interfacial heat transfer • Inelastic scattering contributes to h. BD at temperatures close to D of the softer material where substrate phonon population is still quantum mechanically increasing • Developed JFDMM to take into account some portion of inelastic scattering Microscale Heat Transfer Lab – University of Virginia

Impact How does the knowledge of phonon scattering affect nanoapplications? Microscale Heat Transfer Lab – University of Virginia

Acknowledgments • Pamela Norris, my doctoral advisor and head of the Microscale Heat Transfer laboratory at UVA • Funding from the National Science Foundation (NSF) Graduate Research Fellowship Program (GRFP) • Funding from the Virginia Space Grant Consortium (VSGC) • Collaborators: Leslie Phinney (Sandia), Robert Stevens (RIT), Samuel Graham (Ga. Tech), Thomas Beechem (Ga. Tech) Rob Kelly (UVA), Avik Ghosh (UVA), Mikiyas Tsegaye (UVA), David Cahill (UIUC), John Hostetler (Trumpf Photonics), Mike Klopf (Jefferson Lab), Vickie Connors (NASA Langley) • Microscale Heat Transfer Crew – Rich Salaway, Jennifer Simmons, John Duda, Justin Smoyer Microscale Heat Transfer Lab – University of Virginia

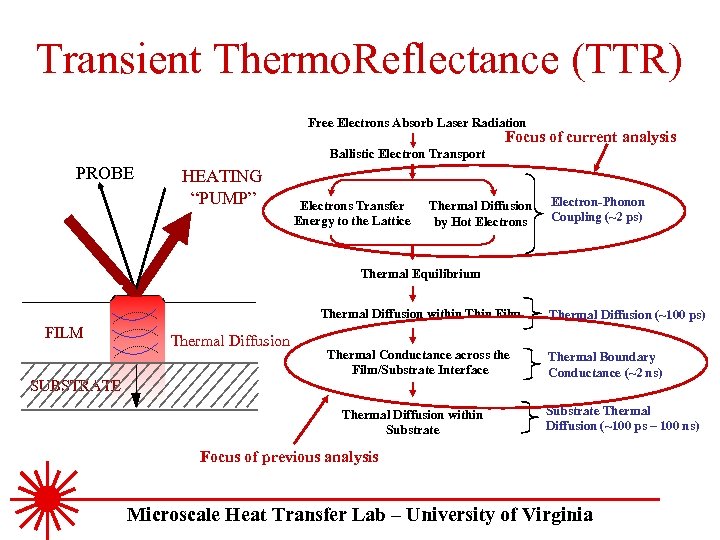Transient Thermo. Reflectance (TTR) Free Electrons Absorb Laser Radiation Focus of current analysis Ballistic Electron Transport PROBE HEATING “PUMP” Electrons Transfer Energy to the Lattice Thermal Diffusion by Hot Electrons Electron-Phonon Coupling (~2 ps) Thermal Equilibrium Thermal Diffusion within Thin Film FILM Thermal Diffusion Thermal Conductance across the Film/Substrate Interface SUBSTRATE Thermal Diffusion within Substrate Thermal Diffusion (~100 ps) Thermal Boundary Conductance (~2 ns) Substrate Thermal Diffusion (~100 ps – 100 ns) Focus of previous analysis Microscale Heat Transfer Lab – University of Virginia

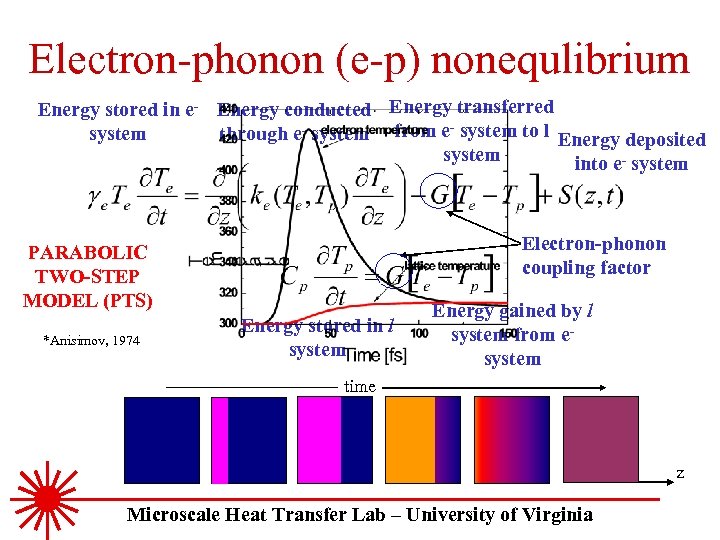Electron-phonon (e-p) nonequlibrium Energy stored in e- Energy conducted Energy transferred through e- system from e- system to l Energy deposited system into e- system Electron-phonon coupling factor PARABOLIC TWO-STEP MODEL (PTS) *Anisimov, 1974 Energy stored in l system Energy gained by l system from esystem time z Microscale Heat Transfer Lab – University of Virginia

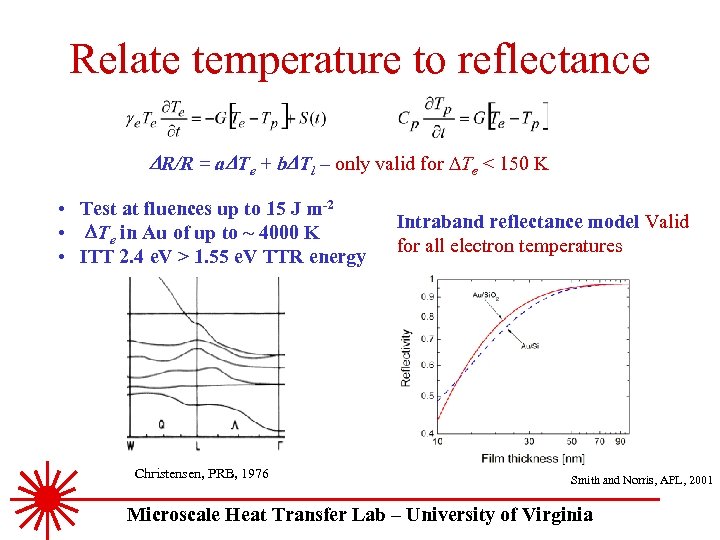Relate temperature to reflectance DR/R = a. DTe + b. DTl – only valid for DTe < 150 K • Test at fluences up to 15 J m-2 • DTe in Au of up to ~ 4000 K • ITT 2. 4 e. V > 1. 55 e. V TTR energy Christensen, PRB, 1976 Intraband reflectance model Valid for all electron temperatures Smith and Norris, APL, 2001 Microscale Heat Transfer Lab – University of Virginia

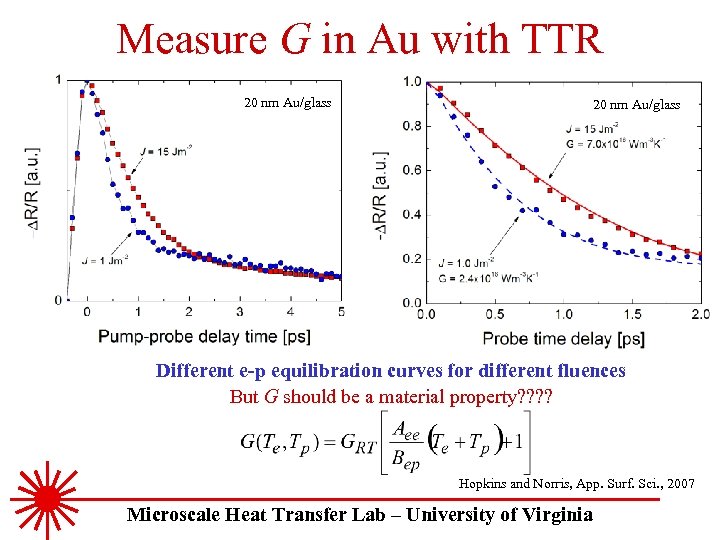Measure G in Au with TTR 20 nm Au/glass Different e-p equilibration curves for different fluences But G should be a material property? ? Hopkins and Norris, App. Surf. Sci. , 2007 Microscale Heat Transfer Lab – University of Virginia

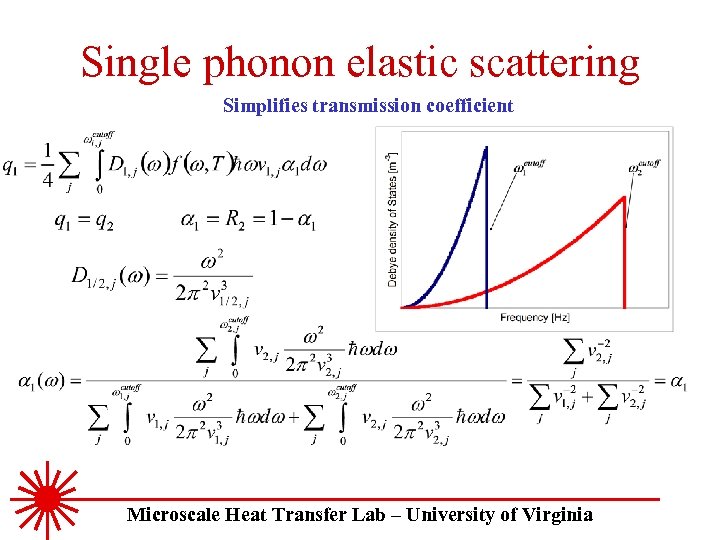Single phonon elastic scattering Simplifies transmission coefficient Microscale Heat Transfer Lab – University of Virginia

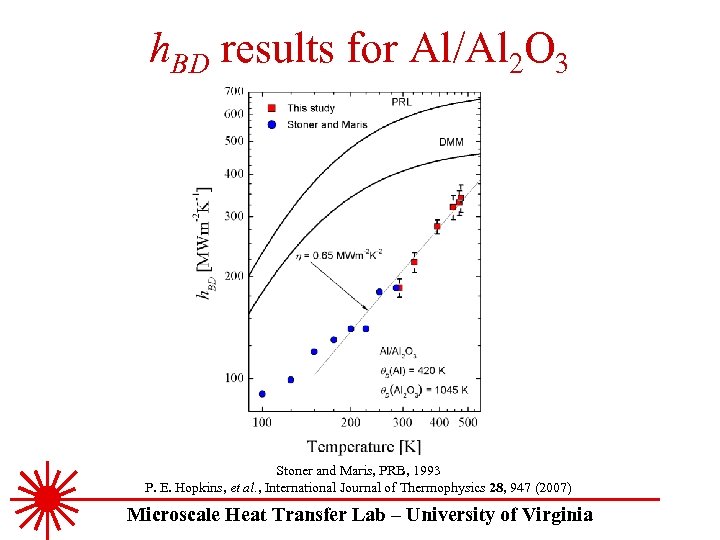h. BD results for Al/Al 2 O 3 Stoner and Maris, PRB, 1993 P. E. Hopkins, et al. , International Journal of Thermophysics 28, 947 (2007) Microscale Heat Transfer Lab – University of Virginia

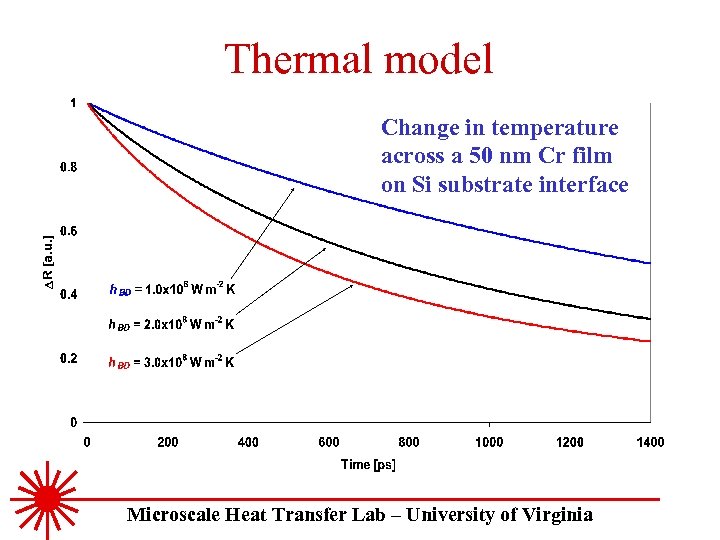Thermal model Change in temperature across a 50 nm Cr film on Si substrate interface Microscale Heat Transfer Lab – University of Virginia

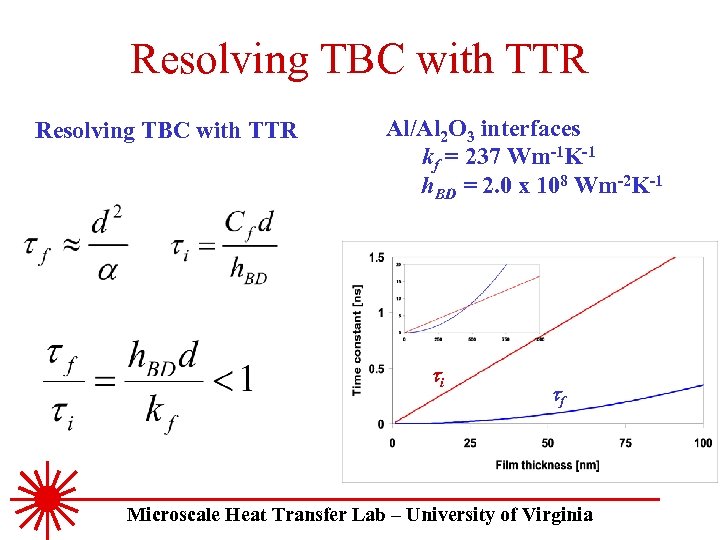Resolving TBC with TTR Al/Al 2 O 3 interfaces kf = 237 Wm-1 K-1 h. BD = 2. 0 x 108 Wm-2 K-1 ti tf Microscale Heat Transfer Lab – University of Virginia

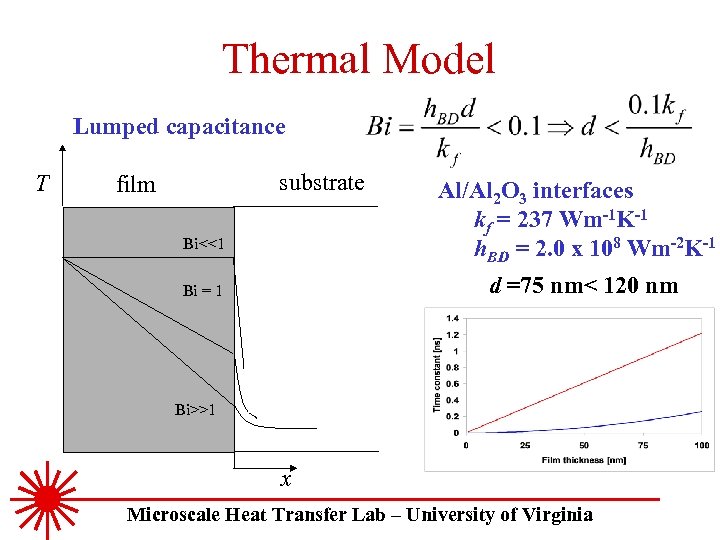Thermal Model Lumped capacitance T substrate film Bi<<1 Al/Al 2 O 3 interfaces kf = 237 Wm-1 K-1 h. BD = 2. 0 x 108 Wm-2 K-1 d =75 nm< 120 nm Bi = 1 Bi>>1 x Microscale Heat Transfer Lab – University of Virginia

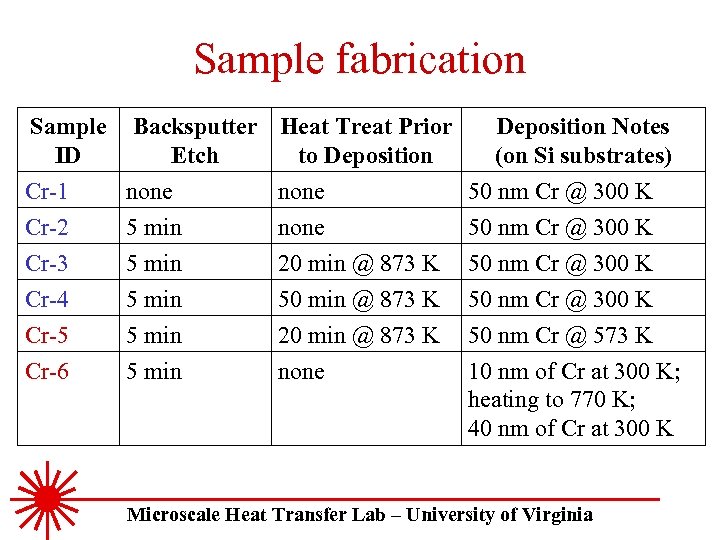Sample fabrication Sample Backsputter Heat Treat Prior Deposition Notes ID Etch to Deposition (on Si substrates) Cr-1 none 50 nm Cr @ 300 K Cr-2 5 min none 50 nm Cr @ 300 K Cr-3 Cr-4 Cr-5 Cr-6 5 min 20 min @ 873 K 50 min @ 873 K 20 min @ 873 K none 50 nm Cr @ 300 K 50 nm Cr @ 573 K 10 nm of Cr at 300 K; heating to 770 K; 40 nm of Cr at 300 K Microscale Heat Transfer Lab – University of Virginia

Interface characterization Auger electron spectroscopy (AES) Electron bombardment e- [3 ke. V] Ionization Relaxation and Auger emission Monitor energy Vacuum Energy Higher levels Core level Microscale Heat Transfer Lab – University of Virginia

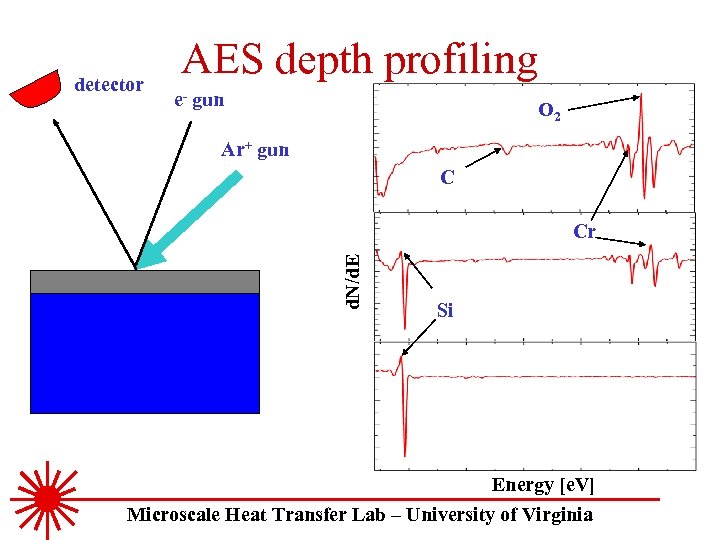detector AES depth profiling e- gun O 2 Ar+ gun C d. N/d. E Cr Si Energy [e. V] Microscale Heat Transfer Lab – University of Virginia

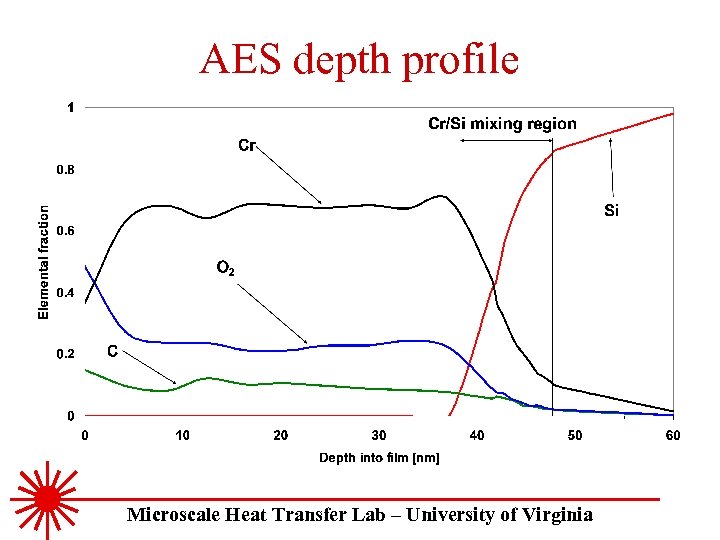AES depth profile Microscale Heat Transfer Lab – University of Virginia

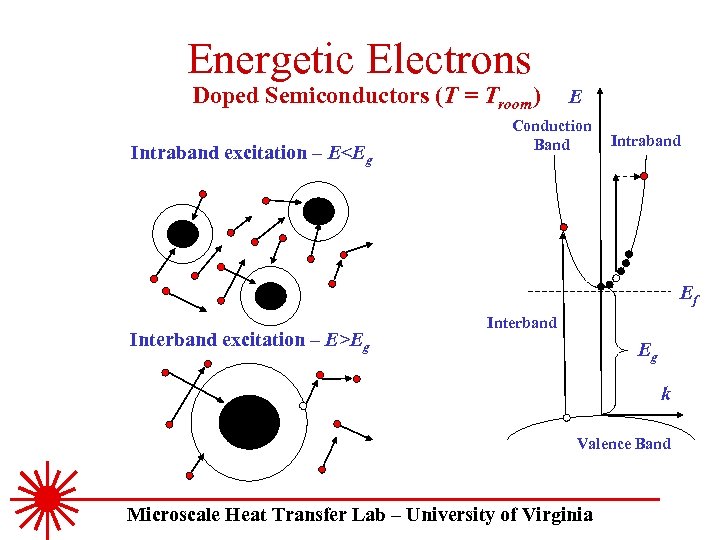Energetic Electrons Doped Semiconductors (T = Troom) Intraband excitation – EEg Interband Eg k Valence Band Microscale Heat Transfer Lab – University of Virginia

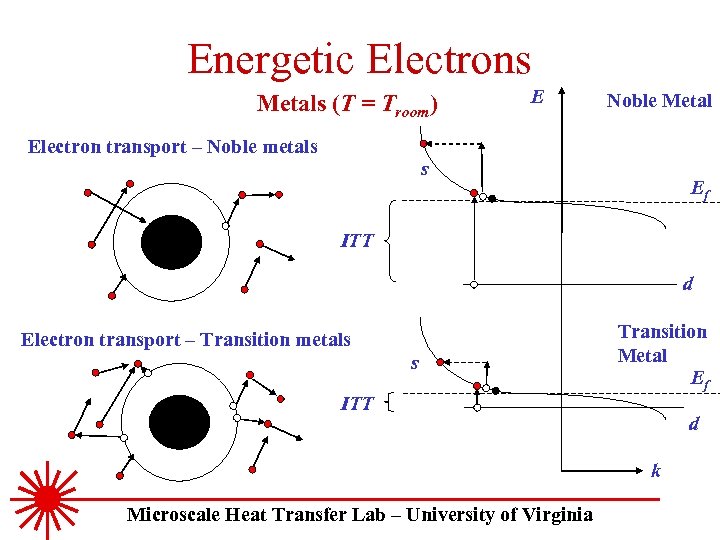Energetic Electrons Metals (T = Troom) E Noble Metal Electron transport – Noble metals s Ef ITT d Electron transport – Transition metals s ITT Transition Metal Ef d k Microscale Heat Transfer Lab – University of Virginia

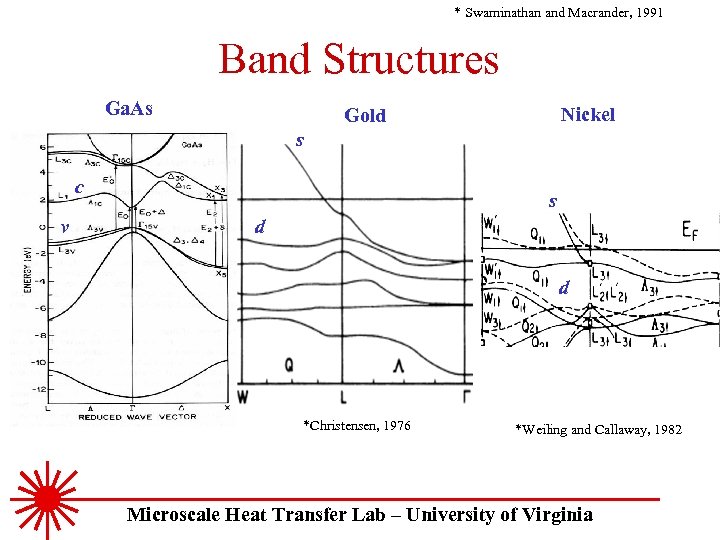* Swaminathan and Macrander, 1991 Band Structures Ga. As Nickel Gold s c v s d d *Christensen, 1976 *Weiling and Callaway, 1982 Microscale Heat Transfer Lab – University of Virginia

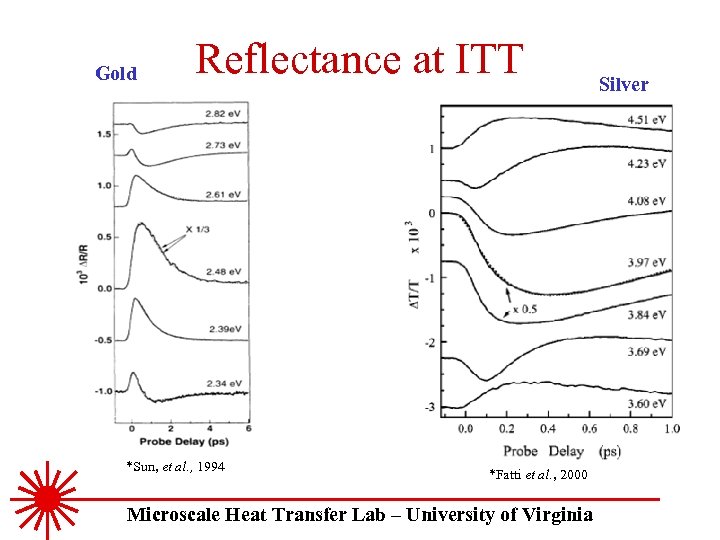Gold Reflectance at ITT *Sun, et al. , 1994 *Fatti et al. , 2000 Microscale Heat Transfer Lab – University of Virginia Silver

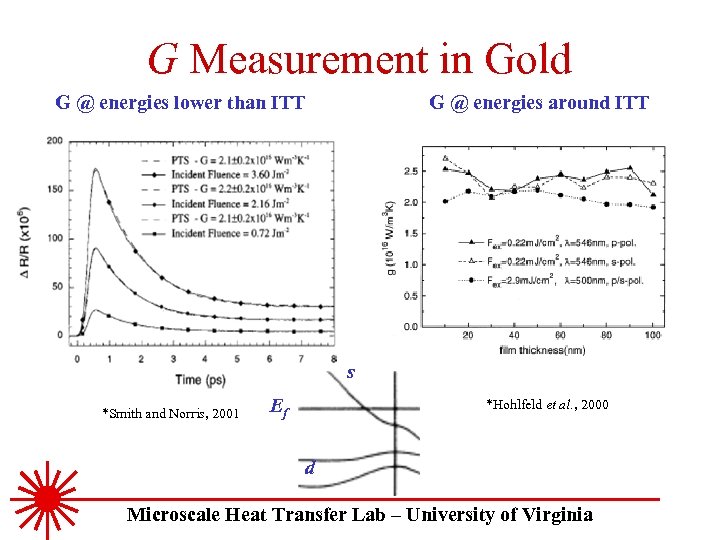G Measurement in Gold G @ energies lower than ITT G @ energies around ITT s *Smith and Norris, 2001 Ef *Hohlfeld et al. , 2000 d Microscale Heat Transfer Lab – University of Virginia

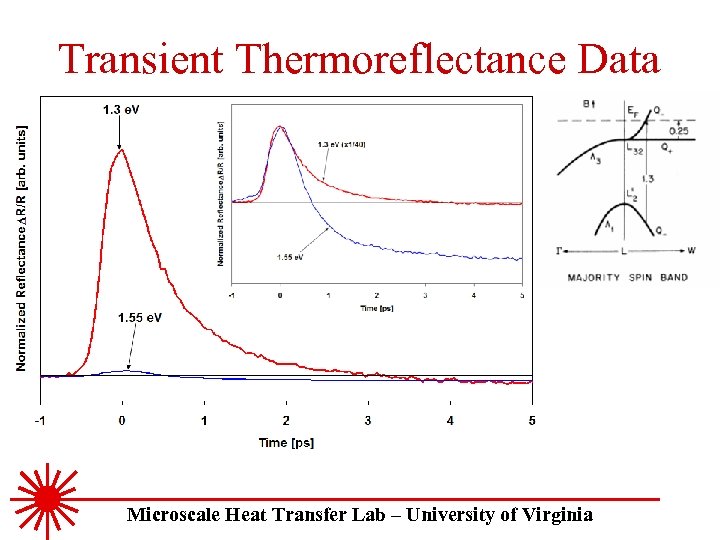Transient Thermoreflectance Data Microscale Heat Transfer Lab – University of Virginia

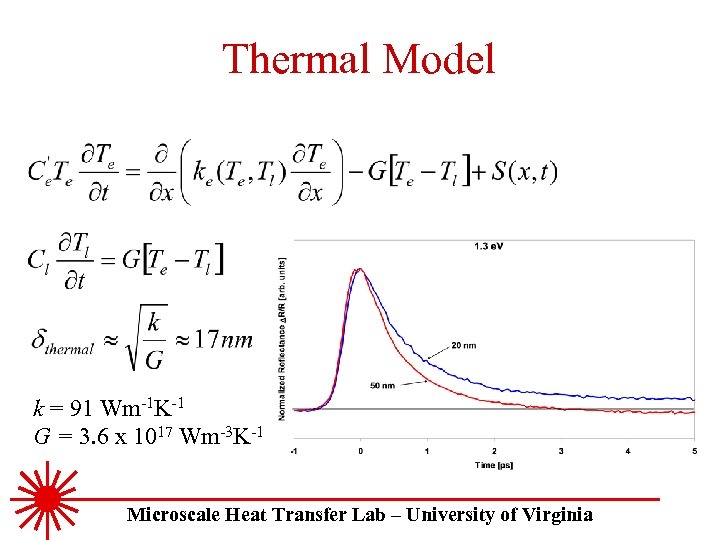Thermal Model k = 91 Wm-1 K-1 G = 3. 6 x 1017 Wm-3 K-1 Microscale Heat Transfer Lab – University of Virginia

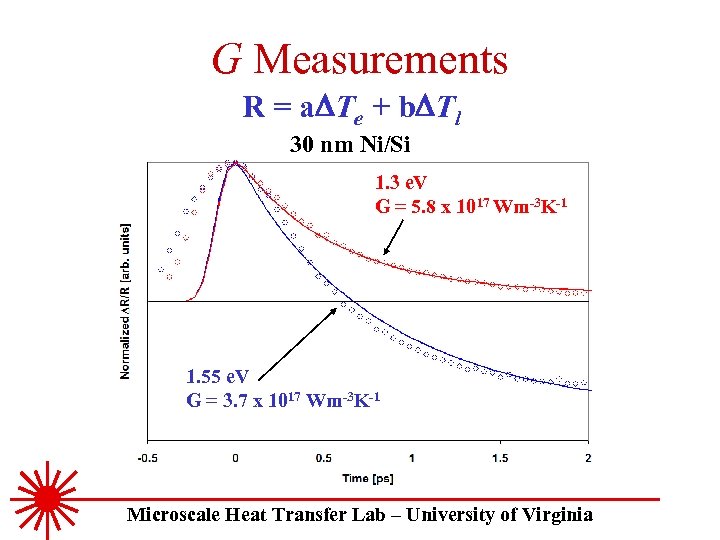G Measurements R = a. DTe + b. DTl 30 nm Ni/Si 1. 3 e. V G = 5. 8 x 1017 Wm-3 K-1 1. 55 e. V G = 3. 7 x 1017 Wm-3 K-1 Microscale Heat Transfer Lab – University of Virginia

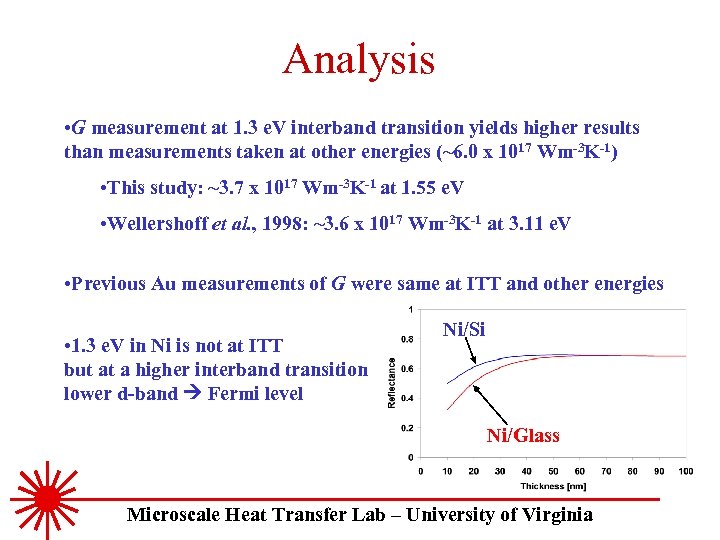Analysis • G measurement at 1. 3 e. V interband transition yields higher results than measurements taken at other energies (~6. 0 x 1017 Wm-3 K-1) • This study: ~3. 7 x 1017 Wm-3 K-1 at 1. 55 e. V • Wellershoff et al. , 1998: ~3. 6 x 1017 Wm-3 K-1 at 3. 11 e. V • Previous Au measurements of G were same at ITT and other energies • 1. 3 e. V in Ni is not at ITT but at a higher interband transition lower d-band Fermi level Ni/Si Ni/Glass Microscale Heat Transfer Lab – University of Virginia

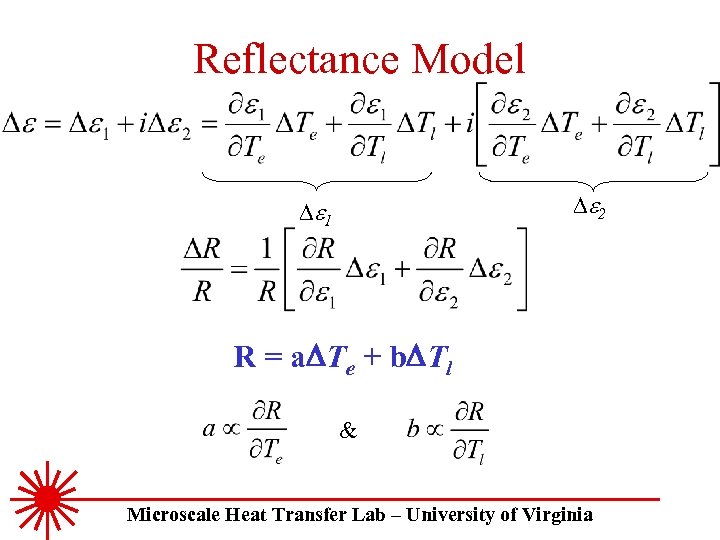Reflectance Model De 2 De 1 R = a. DTe + b. DTl & Microscale Heat Transfer Lab – University of Virginia

How do we define temperature? • Temperature is an equilibrium property • How can we define temperature when there is a nonequilibrium (TTM)? Consider case of homogeneous heating in Au t > tee Temporally • Both e- and phonon systems are in local thermal equilibrium • When e- scatters and emits phonon, e- system redistributes into a new temperature distribution (lower T). What about e- substrate scattering work? • Homogeneous heating so lumped capacitance h. BDe-=1 E 8 Wm-2 K-1 d=50 nm ke=317 Bi =. 02 very conservative Microscale Heat Transfer Lab – University of Virginia

How do we define temperature? • However, how can we determine temperature spatially if there is a thermal gradient? • Can temperature, which is an equilibrium concept, still be invoked in a nonequilibrium process such as heat conduction? (Cahill, JAP, 2003) Consider 1 D conduction Mean free path Kinetic Theory speed #Collisions/time Box is 4 long Cannot resolve local temperature Can resolve local temperature *Since equilibrium is achieved through multiple collisions at Te=Tl=300, Q~1 E 13, ~1 nm d~15 nm Microscale Heat Transfer Lab – University of Virginia ~1 E 4 m/s

Joint frequency DMM JFDMM Weighting factor x is simply a percentage of the composition of each material in the unit volume (M=atomic mass) (N=number of oscillators per unit volume) Microscale Heat Transfer Lab – University of Virginia

Analysis • Inelastic scattering – DMM does not account for this • Data at solid-solid interfaces taken at temperatures around Debye temperature show linear trend • DMM predicts flattening of predicted h. BD around Debye temperature • Accounting for substrate phonons in DMM improves prediction (JFDMM) DMM JFDMM PRL Inelastic phonon radiation limit (IPRL) Is there an upper limit to inelastic scattering? Microscale Heat Transfer Lab – University of Virginia

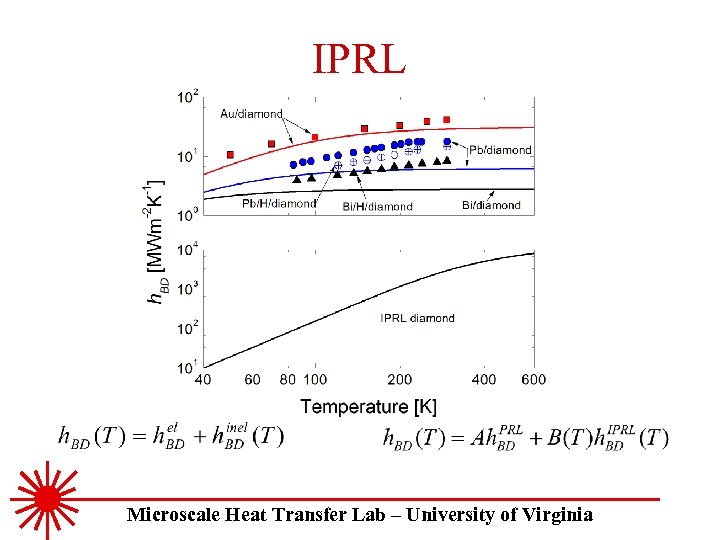IPRL Microscale Heat Transfer Lab – University of Virginia

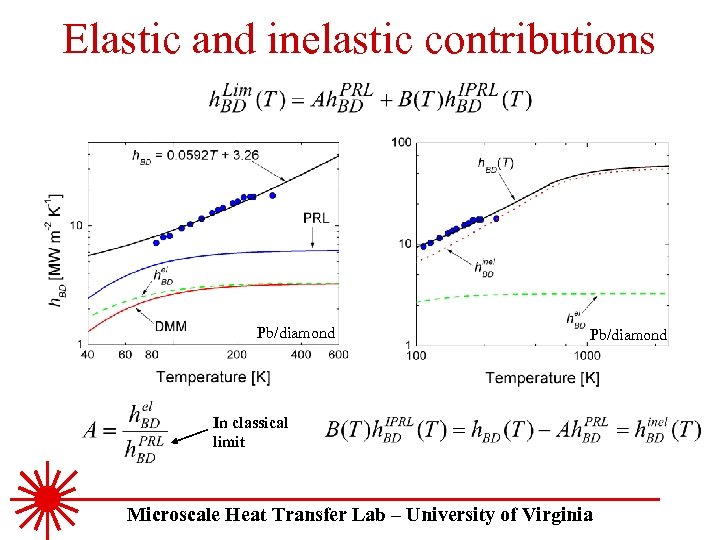Elastic and inelastic contributions Pb/diamond In classical limit Microscale Heat Transfer Lab – University of Virginia

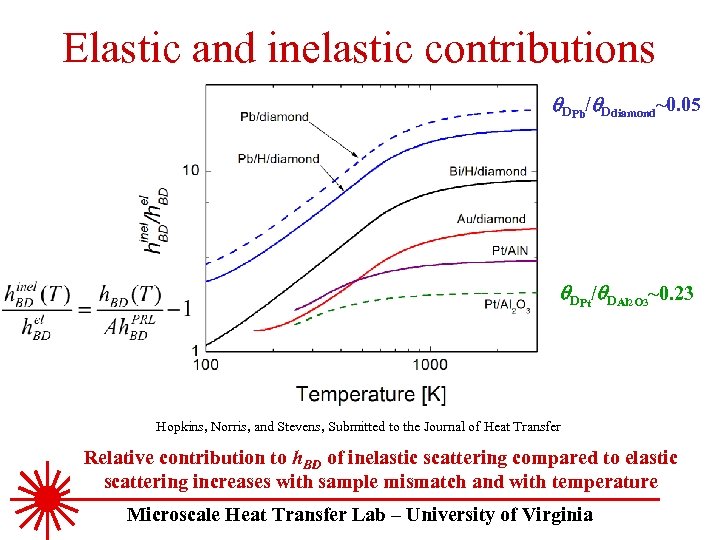Elastic and inelastic contributions DPb/ Ddiamond~0. 05 DPt/ DAl 2 O 3~0. 23 Hopkins, Norris, and Stevens, Submitted to the Journal of Heat Transfer Relative contribution to h. BD of inelastic scattering compared to elastic scattering increases with sample mismatch and with temperature Microscale Heat Transfer Lab – University of Virginia

Future directions Thermal testing in novel nanostructures CNT and nanocomposites Microscale Heat Transfer Lab – University of Virginia

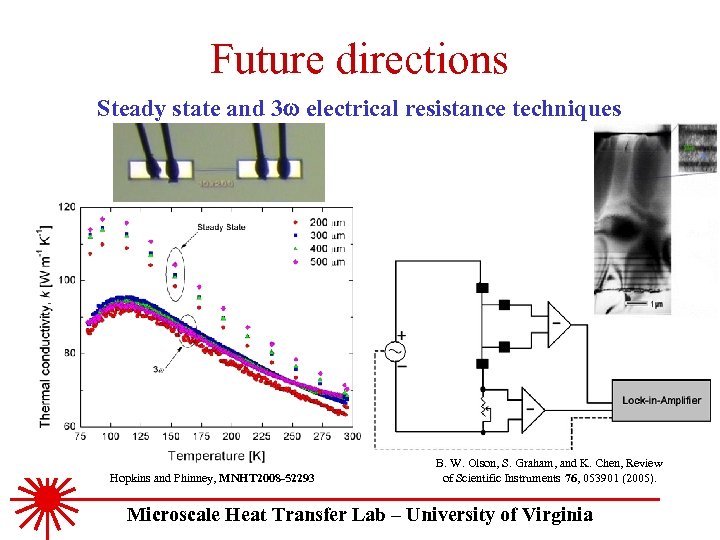Future directions Steady state and 3 w electrical resistance techniques Hopkins and Phinney, MNHT 2008 -52293 B. W. Olson, S. Graham, and K. Chen, Review of Scientific Instruments 76, 053901 (2005). Microscale Heat Transfer Lab – University of Virginia

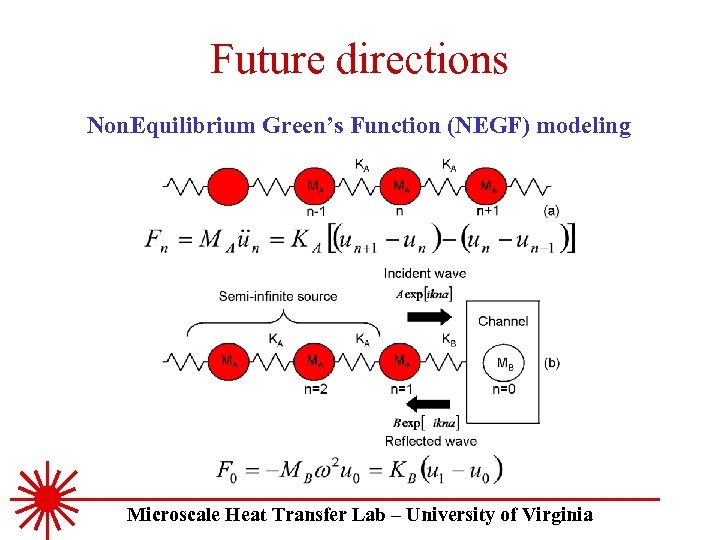Future directions Non. Equilibrium Green’s Function (NEGF) modeling Microscale Heat Transfer Lab – University of Virginia

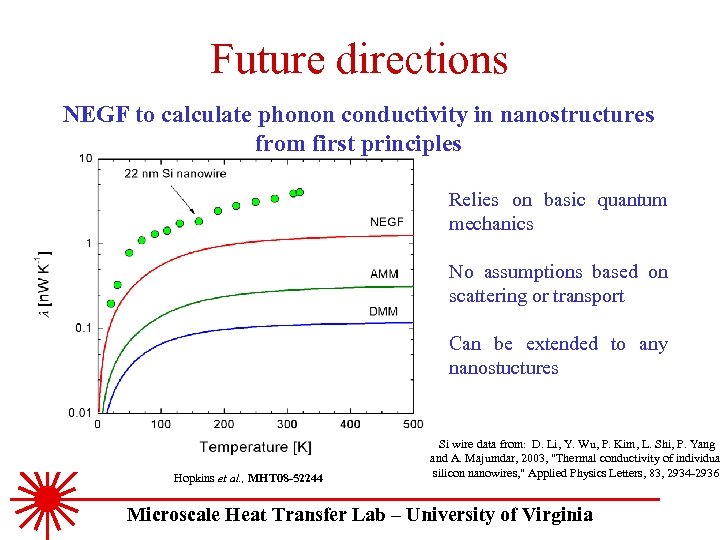Future directions NEGF to calculate phonon conductivity in nanostructures from first principles Relies on basic quantum mechanics No assumptions based on scattering or transport Can be extended to any nanostuctures Hopkins et al. , MHT 08 -52244 Si wire data from: D. Li, Y. Wu, P. Kim, L. Shi, P. Yang and A. Majumdar, 2003, "Thermal conductivity of individua silicon nanowires, " Applied Physics Letters, 83, 2934 -2936. Microscale Heat Transfer Lab – University of Virginia

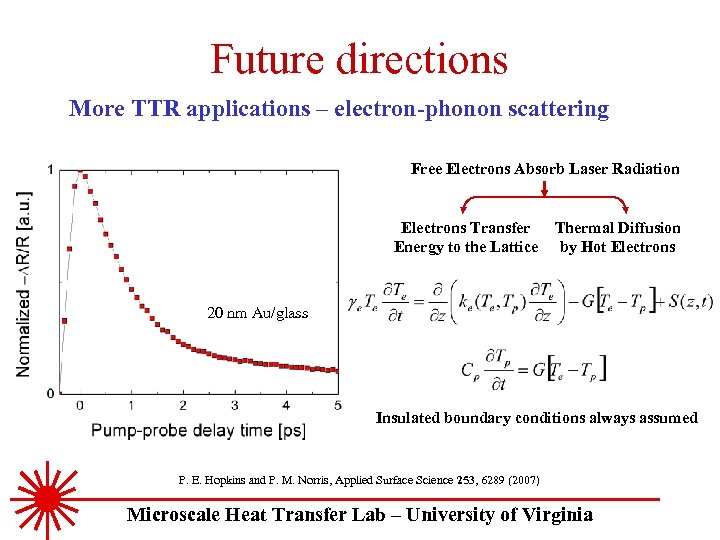Future directions More TTR applications – electron-phonon scattering Free Electrons Absorb Laser Radiation Electrons Transfer Energy to the Lattice Thermal Diffusion by Hot Electrons 20 nm Au/glass Insulated boundary conditions always assumed P. E. Hopkins and P. M. Norris, Applied Surface Science 253, 6289 (2007) Microscale Heat Transfer Lab – University of Virginia

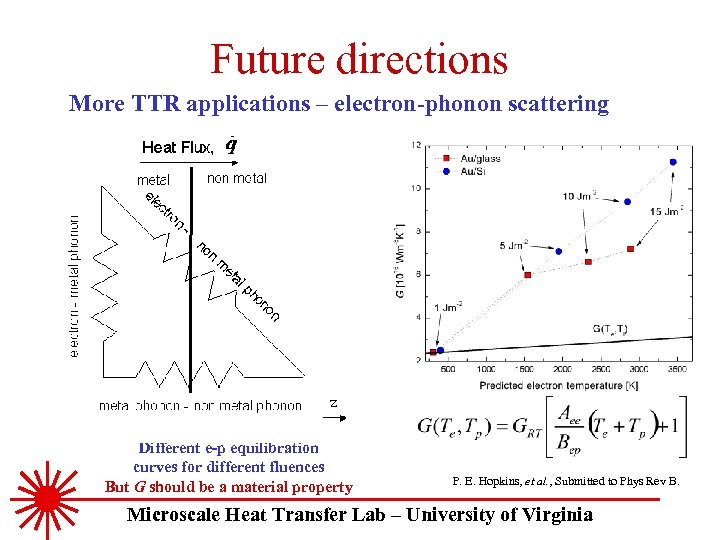Future directions More TTR applications – electron-phonon scattering z Different e-p equilibration curves for different fluences But G should be a material property P. E. Hopkins, et al. , Submitted to Phys Rev B. Microscale Heat Transfer Lab – University of Virginia

Future directions • Extend nanoscale thermophysics to realistic low dimensional nanostructures • Electrically based resistance techniques to measure thermal transport and thermophysical properties of nanomaterials • NEGF formalism for accurate modeling of real nanosystems • TTR technique to measure electron-phonon coupling and interfacial thermal transport Microscale Heat Transfer Lab – University of Virginia