Phasing and Missing data recovery in Family Trios

Phasing and Missing data recovery in Family Trios D. Brinza J. He W. Mao A. Zelikovsky CS Department International Workshop on Bioinformatics Research and Applications, May 2005

Overview • SNP, Genotypes and Haplotypes • Phasing & Missing Data Recovery for Trios • Family trios & trio constraints • ILP for Pure Parsimony • Trio phasing without recombinations International Workshop on Bioinformatics Research and Applications, May 2005

SNP, Genotypes and Haplotypes • • Length of Human Genome 3 109 #Single nucleotide polymorphism (SNPs) 1 107 SNPs are mostly biallelic, e. g. , A C Minor allele frequency should be considerable e. g. >. 1% Difference b/w ALL people 0. 25% (b/w any 2 0. 1%) Diploid = two different copies of each chromosome Haplotype = description of a single copy (expensive) – example: 00110101 (0 is for major, 1 is for minor allele) • Genotype = description of the mixed two copies – example 01122110 (0=00, 1=11, 2=01) • International Hapmap project: www. hapmap. org International Workshop on Bioinformatics Research and Applications, May 2005

Population Phasing Problem • Given genotype n m matrix G – n genotype-rows with m snips-columns • Find haplotype 2 n m matrix H – 2 n haplotyp-rows with m snips-columns – each g genotype is explained with two haplotypes h 1, h 2 Remarks: h 1 = 0011010 h 2 = 0110110 g = 0212210 – For an individual with k heterozygous sites (2’s), 2 k-1 haplotype pairs can be a possible solution – This is hopeless without a genetic model – Programs: PHASE, HAPLOTYPER, HAP, GERBIL, DPPH, etc. International Workshop on Bioinformatics Research and Applications, May 2005

Family Trios & Trio Constraints • Common genotype data are in family trios consisting of two parents and one offspring • Trio data allows to recover offspring haplotypes with higher confidence. • Haplotype reconstruction should satisfy trio constraints. • Example: – If genotypes are – Then haplotypes are f=22 m=02 k=01 f 1=10 m 1=01 k 1=01 f 2=01 m 2=00 k 2=01 Only if f=m=k=22, the ambiguity remains International Workshop on Bioinformatics Research and Applications, May 2005

Family Trio Phasing • Parental Trio Phasing Problem – Given a set of genotype partitioned into family trios – Find for each trio a quartet of parent haplotypes which agree with all three genotypes: • Parental haplotypes agree with parental genotypes • Inherited parental haplotypes agree with offspring genotype • General Trio Phasing Problem – Find (additionally) for each offspring the “true” recombination of inherited parental haplotypes International Workshop on Bioinformatics Research and Applications, May 2005

ILP for Parental Trio Phasing • • Introduce four template haplotypes {0, 1, 2, ? } Variables: x -- for each possible haplotype y -- for each 2 Objective: Constraints: International Workshop on Bioinformatics Research and Applications, May 2005

Results International Workshop on Bioinformatics Research and Applications, May 2005

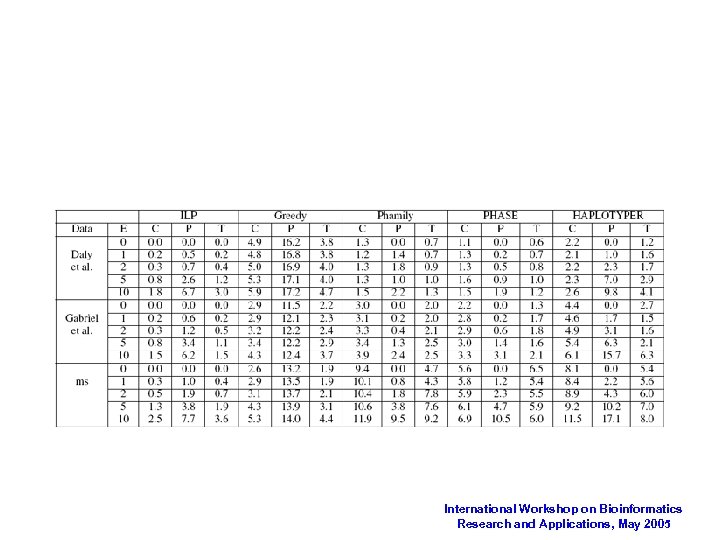
Trio Phasing w/o Crossovers Three phasing methods on the real and simulated data sets Error = % of sites where (best choice of) inherited paternal and maternal haplotypes disagree with the offspring genotype. D = Hamming distance in % between the phased haplotypes and the closest feasible haplotypes. International Workshop on Bioinformatics Research and Applications, May 2005

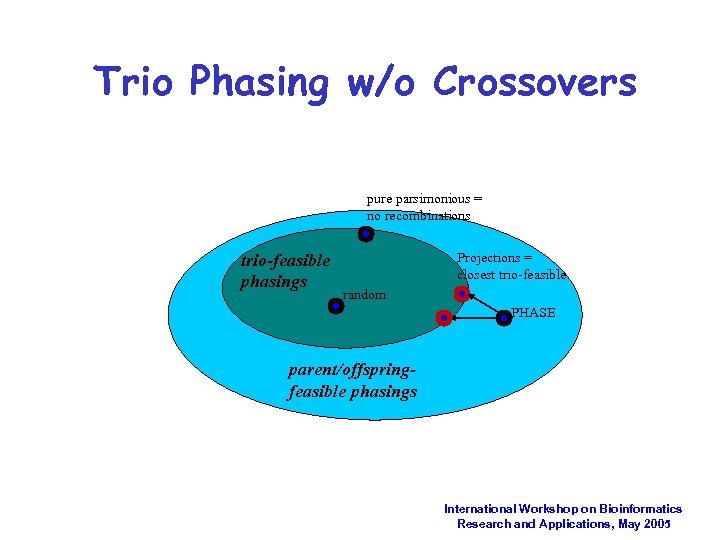Trio Phasing w/o Crossovers pure parsimonious = no recombinations trio-feasible phasings Projections = closest trio-feasible random PHASE parent/offspringfeasible phasings International Workshop on Bioinformatics Research and Applications, May 2005

Missing Data Recovery Problem • Real data often miss some snips – Daly et al data (Chron Disease) 10%-16% – Gabriel et al data (Hapmap) 7%-10% • How to reconstruct missing values? • How to verify reconstruction method? – Scramble extra 10% and reconstruct them • Karp-Halperin (2004) have error rate 2. 8% International Workshop on Bioinformatics Research and Applications, May 2005

Results for Trio Missing Data Recovery International Workshop on Bioinformatics Research and Applications, May 2005

Missing Data Recovery Problem International Workshop on Bioinformatics Research and Applications, May 2005

• Diploid - two haplotypes (different copies of each chromosome) • SNP - single nucleotide site where two or more different • nucleotides occur in a large percentage of population – 0 = willde type/major (frequency) allele – 1 = mutation/minor (frequency) allele • Haplotype - description of a single copy – Example: 00110101 (0 is for major, 1 is for minor allele) • Genotype - description of the mixed two copies – Example: 01122110 (0=00, 1=11, 2=01) International Workshop on Bioinformatics Research and Applications, May 2005

• Formulating the Pure-parsimony Trio Phasing Problem(PTPP) and the Trio Missing Data Recovery Problem (TMDRP) • Two new greedy and integer linear programming (ILP) based methods solving PTPP and TMDRP • New 2 -SNP Statistics (2 SNP) phasing method for unrelated individuals • Extensive experimental validation of proposed methods and comparison with the previously known methods International Workshop on Bioinformatics Research and Applications, May 2005

• PHASE – Bayesian statistical method (Stephens et al. , 2001, 2003) • HAPLOTYPER – proposed a Monte Carlo aproach (Niu et al. , 2002) • Phamily – phase the trio families based on PHASE (Acherman et al. , 2003) • Greedy method for phasing and missing data recovery–by (Halperin and Karp, 2004) • GERBIL – statistical method using maximum likelihood (ML), MST and expectation-maximization (EM) (Kimmel and Shamir, 2005) • SNPHAP – use ML/EM assuming Hardy-Weinberg equilibrium (Clayton et al. , 2004) International Workshop on Bioinformatics Research and Applications, May 2005

• Given a set of family trios of genotypes each with m sites corresponding to m SNPs: – 0 – homozygote with major allele, 1 – homozygote with minor allele, 2 – heterozygote, ? – missing SNP value • Find for each trio four haplotypes h 1, h 2, h 3, h 4 each with m 0 -1 -sites such that: – h 1 and h 2 explain father’s genotype, h 3 and h 4 explain mother’s genotype, h 1 and h 3 explain offspring’s genotype International Workshop on Bioinformatics Research and Applications, May 2005

• Easy to find a feasible solution to TPP (exponential number of feasible solutions) • We pursue parsimonious objective, i. e. , minimization of the total number of haplotypes • Drawback of PP is that when the number of SNPs becomes large (as well as the number of recombinations), then the quality of pure parsimony phasing is diminishing • Partition the genotypes into blocks • In case of trio data we do not have joining blocks problem • Pure-Parsimony Trio Phasing (PPTP). Given 3 n genotypes corresponding to n family trios find minimum number of distinct haplotypes explaining all trios International Workshop on Bioinformatics Research and Applications, May 2005

• Proposed by Halperin et al. in “Perfect phylogeny and haplotype assignment” (2004) • For each trio we introduce four partial haplotypes with SNPs 0, 1 and ? • Algorithm iteratively finds the complete haplotype which covers the maximum possible number of partial haplotypes, removes this set of resolved partial haplotypes and continues in that manner • The drawback of this method is introducing errors to trio constraint International Workshop on Bioinformatics Research and Applications, May 2005

• For each trio we introduce four template haplotypes {0, 1, 2, ? } – 0, 1 – correspond to fully resolved haplotypes, 2 – comes in SNPs corresponding to the genotypes 2’s, ? – unconstrained SNPs • Variables: – for each possible haplotype i, xi {0, 1}, – for each heterozigous SNP j in each template, yj {0, 1} International Workshop on Bioinformatics Research and Applications, May 2005

International Workshop on Bioinformatics Research and Applications, May 2005