PFTWBWTF l Motivation for Priority Queue Ø Solve

PFTWBWTF? l Motivation for Priority. Queue Ø Solve top M of N, Autocomplete Ø Lead-in to Huffman Compression l Details of Priority. Queue Ø From conceptual to actual implementation l Streams in Java: essential but not so Loop Invariants in programming: essential l Compsci 201, Fall 2016 21. 1

Looking up? Compsci 201, Fall 2016 21. 2

Algorithms and Data Structures l Finding the top M of N elements, consider autocomplete for example Compsci 201, Fall 2016 21. 3

Sometimes simple is good, but … l https: //git. cs. duke. edu/201 fall 16/sorting-stuff/blob/master/src/Top. Msorts. java l Add all elements to an array/list, sort, find last M Ø Advantages? Disadvantages? Ø Do we need to store a 10 -million numbers and sort them to find the top 500? Array. List<Integer> nums = new Array. List<>(); // add 10 -million random integers to nums for(all of 10 -million int values){ nums. add(value); } Collections. sort(nums); top 1 = nums. sub. List(nums. size()-500, nums. size()); Compsci 201, Fall 2016 21. 4

Store only the top (500) numbers … l https: //git. cs. duke. edu/201 fall 16/sorting-stuff/blob/master/src/Top. Msorts. java l Need an efficient structure that keeps elements ordered, but not too ordered Ø Priority. Queue Ø Add elements, remove elements (like Queue) Ø However, remove means "remove smallest" Priority<Integer> pq = new Priority<>(); // add 10 -million random integers to pq? ? ? for(all of 10 -million int values){ pq. add(value); if (pq. size() > 500) pq. remove(); } while (pq. size() > 0) top 2. add(pq. remove()); Compsci 201, Fall 2016 21. 5

Java 8 Streams Aside l l Streams aren't part of 201, but they're useful in this and other situations Ø Create a stream from some source Ø Alter the stream: filter or limit or … Ø Collect results, or for. Each them, or … Chain results of streams: create new streams or terminate the streams, e. g. , limit and for. Each Random r = new Random(1234); Int. Stream is = r. ints(low, high); is. limit(1000000). for. Each(e->System. out. println(e)); Compsci 201, Fall 2016 21. 6

Streams and Big Data l Google originally implemented Map. Reduce Ø https: //en. wikipedia. org/wiki/Map. Reduce now open sourced, e. g. , Hadoop l Distributed Storage and processing Ø Not everything fits on one disk, one computer, . . . Ø How to coordinate and combine data l Lazy evaluation: only compute when needed Ø To some just the even numbers in lazy stream, … Ø Filter the even numbers, sum everything Compsci 201, Fall 2016 21. 7

Why good for autocomplete? l Advantageous to store fewer than a billion terms? Ø Assume terms are "weighted" by popularity Ø We want maximally weighted terms Compsci 201, Fall 2016 21. 8

YAQ, haha! (Yet Another Queue) l What is the dequeue policy for a Queue? Ø Why do we implement Queue with Linked. List Ø Can we remove an element other than first? l How does queue help word-ladder/shortest path? Ø First item enqueued/added is the one we want Ø What if different element is “best”? l Priority. Queue has a different dequeue policy Ø Best item is dequeued, queue manages itself to ensure operations are efficient Compsci 201, Fall 2016 21. 9

Priority. Queue raison d’être l Algorithms Using PQ for efficiency Ø Shortest Path: Google Maps to Internet Routing • How is this like word-ladder? How different? Ø Event based simulation • Coping with explosion in number of particles or things Ø Optimal A* search, game-playing, AI, • Can't explore entire search space, can estimate good move l Data compression facilitated by priority queue Ø All-time best assignment in a Compsci course? • Subject to debate, of course Ø From A-Z, soup-to-nuts, bits to abstractions Compsci 201, Fall 2016 21. 10

Priority Queue sorting l See PQDemo. java, now with streams! Ø https: //git. cs. duke. edu/201 fall 16/sortingstuff/blob/master/src/PQDemo. java Ø code below sorts, complexity? String[] array = {. . . }; // array filled with data Priority. Queue<String> pq = new Priority. Queue<String>(); for(String s : array) pq. add(s); for(int k=0; k < array. length; k++){ array[k] = pq. remove(); } l Bottlenecks, operations in code above Ø Add words one-at-a-time to PQ v. all-at-once Ø We’d like PQ to have tree characteristics, why? Compsci 201, Fall 2016 21. 11

Priority Queue top-M sorting l What if we have lots and lots of data Ø code below sorts top-M elements, complexity? Scanner s = … // initialize; Priority. Queue<String> pq = new Priority. Queue<String>(); while (s. has. Next()) { pq. add(s. next()); if (pq. size() > M) pq. remove(); } l What's advantageous about this code? Ø Store everything and sort everything? Ø Store everything, sort first M? Ø What is complexity of sort: O(n log n) Compsci 201, Fall 2016 21. 12

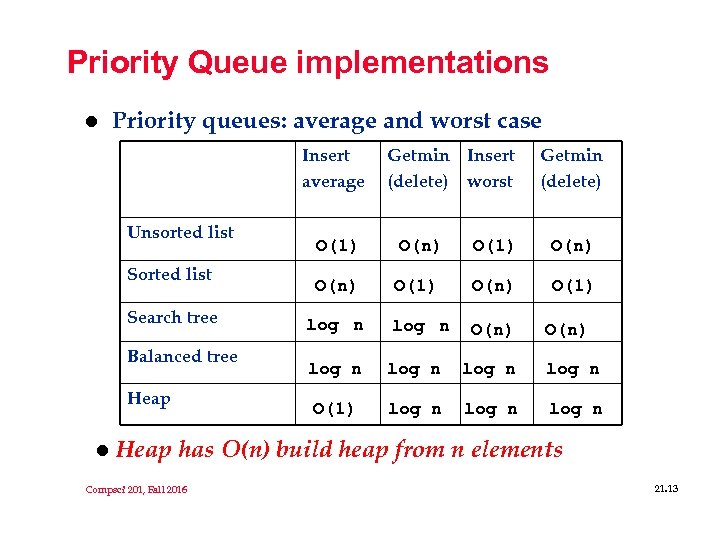
Priority Queue implementations l Priority queues: average and worst case Insert average Unsorted list Search tree Balanced tree Heap l Getmin Insert (delete) worst Getmin (delete) O(1) O(n) O(1) log n O(n) log n O(1) log n O(n) Heap has O(n) build heap from n elements Compsci 201, Fall 2016 21. 13

Craig Gentry Duke '95, Harvard Law, Stanford Compsci Ph. D ACM 2010 Hopper Award for… "Fully homomorphic encryption is a bit like enabling a layperson to perform flawless neurosurgery while blindfolded, and without later remembering the episode. We believe this breakthrough will enable businesses to make more informed decisions, based on more studied analysis, without compromising privacy. " IBM VP, Software Research Compsci 201, Fall 2016 21. 14

Data Structures for Auto. Complete l l l We want M of N, ordered by weight/importance Ø Typically N is very, very large We can use brute force, if we type "the", find everything that matches "the", sort by weight, done Ø O(N) to search through everything Ø O(M log M) to sort list of M items We can use priority queue, insert matches of "the" Ø If we want only top 50 of M, limit size of PQ Ø O(log M) for PQ, done N times… O(N log M) Compsci 201, Fall 2016 21. 15

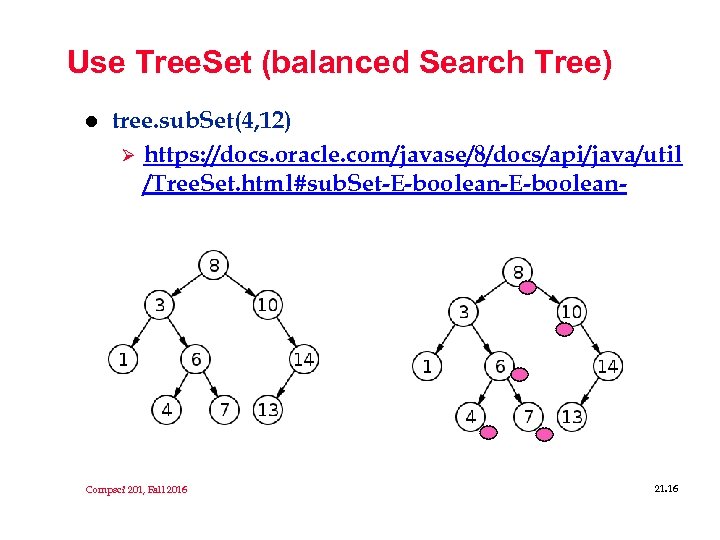
Use Tree. Set (balanced Search Tree) l tree. sub. Set(4, 12) Ø https: //docs. oracle. com/javase/8/docs/api/java/util /Tree. Set. html#sub. Set-E-boolean- Compsci 201, Fall 2016 21. 16

Trie l l re. TRIEval structure supporting very efficient lookup, O(w) where w is length of query, regardless of number of entries in structure! Ø 26 -way branching Ø N-way branching Map if sparse branching Compsci 201, Fall 2016 21. 17

Trie, and Trie again l https: //git. cs. duke. edu/201 fall 16/set-examples/blob/master/src/Trie. Set. java l Method. contains is similar to others Ø What does Node class look like? public boolean contains(String s) { Node t = my. Root; for (int k = 0; k < s. length(); k++) { char ch = s. char. At(k); t = t. children. get(ch); if (t == null) return false; // no path below? done } return t. is. Word; // was this marked as a word? } Compsci 201, Fall 2016 21. 18

Priority Queue implementation l Heap data structure is fast and reasonably simple Ø Uses array, contiguous memory, good performance with cache and more l Changing comparison when calculating priority? Ø Create object to replace, or in lieu of compare. To • Comparable interface compares this to passed object • Comparator interface compares two passed objects Ø Comparisons: compare. To() and compare() • Compare two objects (parameters or self and parameter) • Returns – 1, 0, +1 depending on <, ==, > Compsci 201, Fall 2016 21. 19

Creating Heaps l Heap: array-based implementation of binary tree used for implementing priority queues: Ø add/insert, peek/getmin, remove/deletemin, O(? ? ? ) l Array minimizes storage (no explicit pointers), faster too, contiguous (cache) and indexing Heap has shape property and heap/value property Ø shape: tree filled at all levels (except perhaps last) and filled left-to-right (complete binary tree) Ø each node has value smaller than both children l Compsci 201, Fall 2016 21. 20

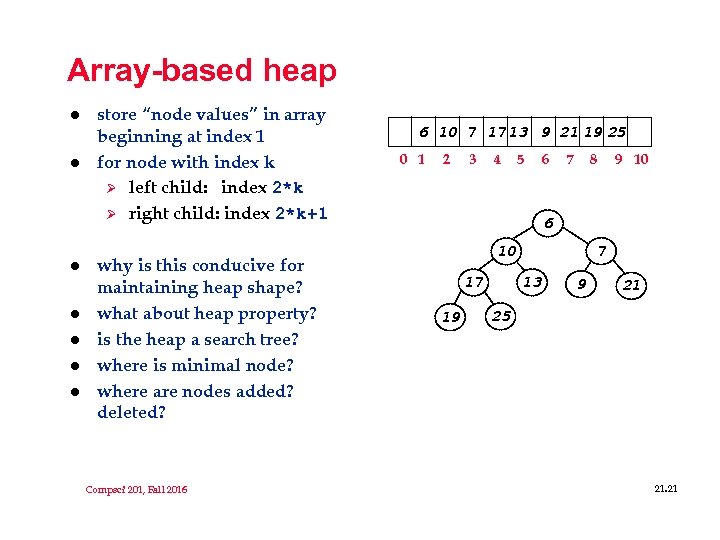
Array-based heap l l l l store “node values” in array beginning at index 1 for node with index k Ø left child: index 2*k Ø right child: index 2*k+1 why is this conducive for maintaining heap shape? what about heap property? is the heap a search tree? where is minimal node? where are nodes added? deleted? Compsci 201, Fall 2016 6 10 7 17 13 9 21 19 25 0 1 2 3 4 5 6 7 8 9 10 6 7 10 13 17 19 9 21 25 21. 21

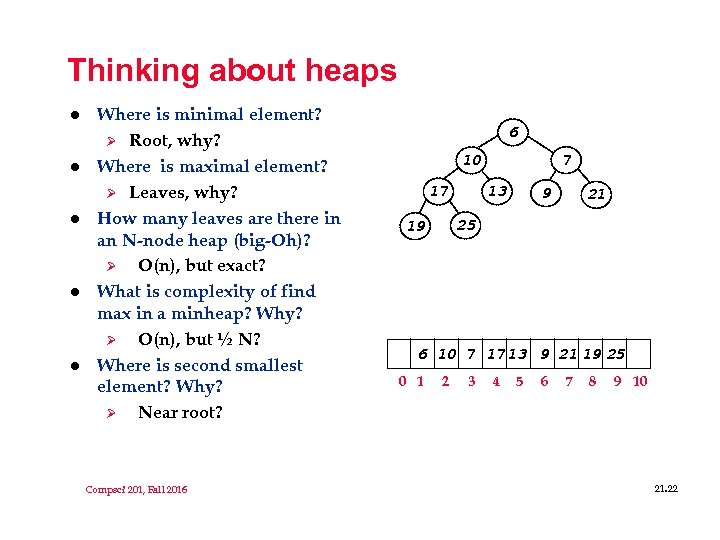
Thinking about heaps l l l Where is minimal element? Ø Root, why? Where is maximal element? Ø Leaves, why? How many leaves are there in an N-node heap (big-Oh)? Ø O(n), but exact? What is complexity of find max in a minheap? Why? Ø O(n), but ½ N? Where is second smallest element? Why? Ø Near root? Compsci 201, Fall 2016 6 7 10 13 17 9 21 25 19 6 10 7 17 13 9 21 19 25 0 1 2 3 4 5 6 7 8 9 10 21. 22

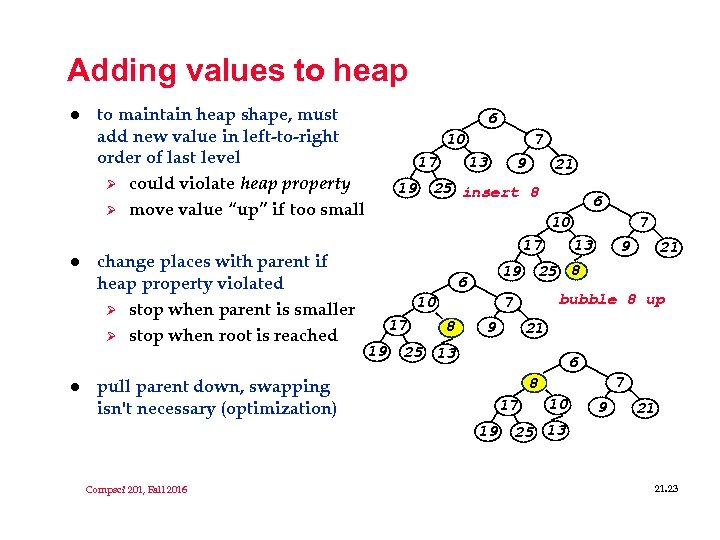
Adding values to heap l l l to maintain heap shape, must add new value in left-to-right order of last level Ø could violate heap property Ø move value “up” if too small change places with parent if heap property violated Ø stop when parent is smaller Ø stop when root is reached 6 7 10 13 17 19 21 25 insert 8 6 7 10 13 17 17 19 8 21 bubble 8 up 7 10 9 25 8 19 6 9 21 25 13 6 7 8 pull parent down, swapping isn't necessary (optimization) 17 19 Compsci 201, Fall 2016 9 10 9 21 25 13 21. 23

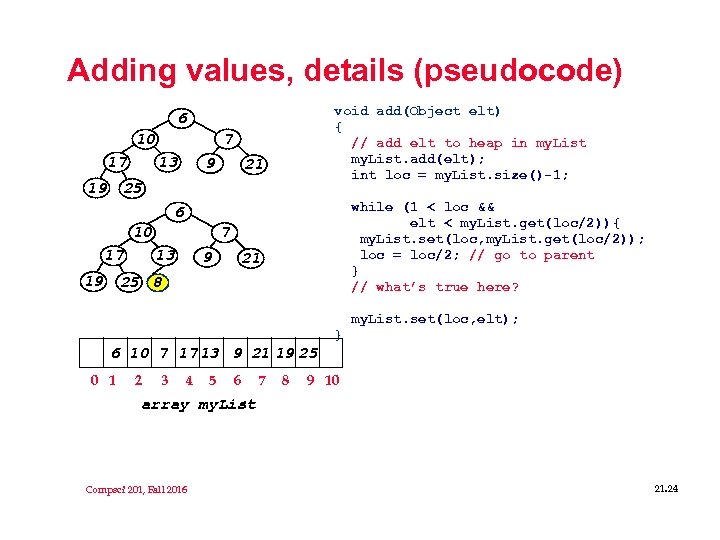
Adding values, details (pseudocode) void add(Object elt) { // add elt to heap in my. List. add(elt); int loc = my. List. size()-1; 6 7 10 13 17 19 9 21 25 while (1 < loc && elt < my. List. get(loc/2)){ my. List. set(loc, my. List. get(loc/2)); loc = loc/2; // go to parent } // what’s true here? 6 7 10 13 17 19 9 21 25 8 my. List. set(loc, elt); } 6 10 7 17 13 9 21 19 25 0 1 2 3 4 5 6 7 8 9 10 array my. List Compsci 201, Fall 2016 21. 24

Removing minimal element l l Where is minimal element? 6 Ø If we remove it, what changes, 7 10 shape/property? 13 17 9 21 How can we maintain shape? 19 25 25 Ø “last” element moves to root 7 10 Ø What property is violated? 13 17 9 21 After moving last element, 19 subtrees of root are heaps, why? 7 Ø Move root down (pull child 25 10 up) does it matter where? 13 17 9 21 When can we stop “re-heaping”? 19 7 Ø Less than both children 9 10 Ø Reach a leaf 13 25 17 21 19 Compsci 201, Fall 2016 21. 25

WOTO http: //bit. ly/201 fall 16 -pq Heapify, magnify, stupify Compsci 201, Fall 2016 21. 26

Views of programming l Writing code from the method/function view is pretty similar across languages Ø Organizing methods is different, organizing code is different, not all languages have classes, Ø Loops, arrays, arithmetic, … l Program using abstractions and high level concepts Ø Do we need to understand 32 -bit twoscomplement storage to understand x =x+1? Ø Do we need to understand how arrays map to contiguous memory to use Array. Lists? Compsci 201, Fall 2016 21. 27

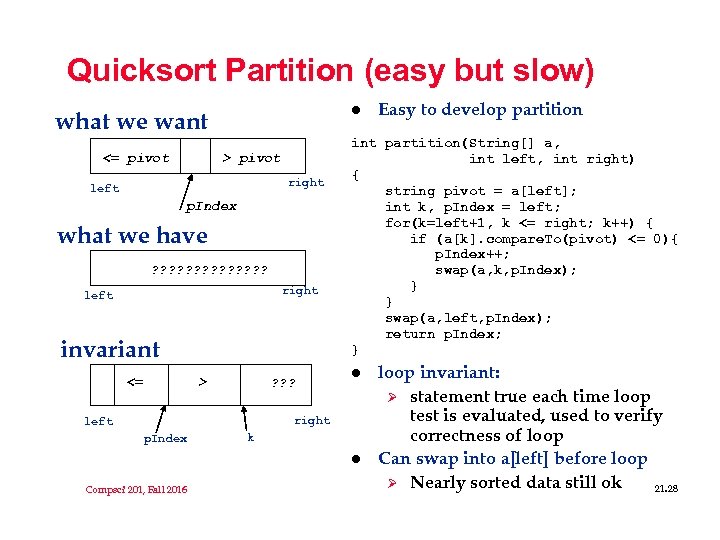
Quicksort Partition (easy but slow) l what we want <= pivot > pivot right left p. Index what we have ? ? ? ? right left invariant <= > ? ? ? int partition(String[] a, int left, int right) { string pivot = a[left]; int k, p. Index = left; for(k=left+1, k <= right; k++) { if (a[k]. compare. To(pivot) <= 0){ p. Index++; swap(a, k, p. Index); } } swap(a, left, p. Index); return p. Index; } l right left p. Index k l Compsci 201, Fall 2016 Easy to develop partition loop invariant: Ø statement true each time loop test is evaluated, used to verify correctness of loop Can swap into a[left] before loop Ø Nearly sorted data still ok 21. 28

Developing Loops l l The Science of Programming, David Gries The Discipline of Programming, Edsger Disjkstra Compsci 201, Fall 2016 21. 29

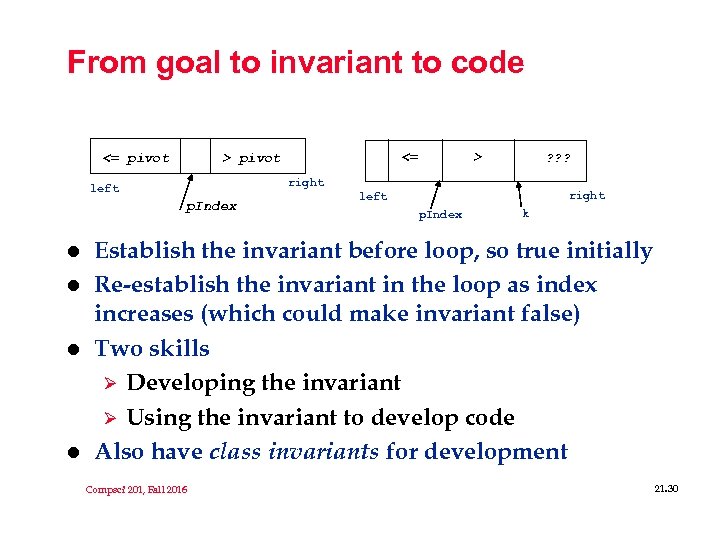
From goal to invariant to code <= pivot p. Index l l l > ? ? ? right left l <= > pivot right left p. Index k Establish the invariant before loop, so true initially Re-establish the invariant in the loop as index increases (which could make invariant false) Two skills Ø Developing the invariant Ø Using the invariant to develop code Also have class invariants for development Compsci 201, Fall 2016 21. 30

what is search? binary search We Teach_CS, Austin, 2016 31 31

Why write the binary search method? l After all, there is Collections. binary. Search Ø Which of several equal keys found? 1, 1, 2, 2, 2, 3, 3, 3 Ø Why does this matter? l Look up the code online!? *!#? Ø http: //stackoverflow. com/questions/6676360/firstoccurrence-in-a-binary-search l Why did you take Compsci 201? Ø How to write/develop? How to randomly permute and hope? Search skills? Compsci 201, Fall 2016 21. 32

Coding Interlude: Reason about code public class Looper { public static void main(String[] args){ int x = 0; while (x < x + 1) { x = x + 1; } System. out. println("value of x = "+x); } } We Teach_CS, Austin, 2016 33

What does this code do? int x = 0; A. while (x < x + 1) { B. x = x + 1; } System. out. println(x); C. D. Compsci 201, Fall 2016 Runs Forever Runs until memory exhausted (a few seconds with 8 Gb) Runs for a second, prints about 2 billion Runs for a second, prints about -2 billion 21. 34

From idea to code http: //bit. ly/ap-csa public static int binary. Search(int[] elements, int target){ int left = 0; int right = elements. length − 1; while (left <= right) { int mid = (left + right) / 2; if (target < elements[mid]) right = mid − 1; else if (target > elements[middle]) left = mid + 1; else return mid; } return − 1; } We Teach_CS, Austin, 2016 35 35

http: //googleresearch. blogspot. com/2006/06/extra-read-all-about-itnearly. html public static int binary. Search(int[] elements, int target) { int left = 0; int right = elements. length − 1; while (left <= right) { int mid = (left + right) / 2; if (target < elements[mid]) right = mid − 1; else if (target > elements[middle]) left = mid + 1; else return mid; } return − 1; } We Teach_CS, Austin, 2016 36 36

What should you remember? 10 2 = 1, 024 31 is about 2 billion 2 Store that many values in memory? We Teach_CS, Austin, 2016 37 37

Don't know much about algebra (left + right)/2 (right - left)/2 + left right/2 - left/2 + 2*left/2 right/2 + left/2 (right + left)/2 We Teach_CS, Austin, 2016 38 38