Петрография изверженных пород 3 курс Лекции — профессор

Петрография изверженных пород 3 курс Лекции - профессор А. Э. Изох Практические занятия: геохимики - доцент Е. Н. Ушакова геологи- ассистенты Р. А. Шелепаев, В. П. Сухоруков нефтяники - преподователь В. А. Широких

Петрография – занимается систематическим описанием и изучением горных пород 1. Наблюдения в поле; 2. Изучение штуфов; 3. Изучение прозрачных шлифов; 4. Исследование рудных минералов 5. Анализ химического, состава пород • Петрография в конечном итоге отвечает на вопросы: • Что это за порода? • Как ее назвать?

Петрология – занимается изучением естественной истории горных пород, их генезиса и преобразования 1. Анализ химического, геохимического и изотопного состава пород и минералов 2. Экспериментальные исследования 3. Расчеты физикохимических параметров • Петрологтя в конечном итоге отвечает на вопросы: • Как образуется горная порода? • Почему она образуется? • Как связаны разные горные породы между собой?

Розенбуш, 1898 Горная порода - минеральные агрегаты составляющие земную кору Современное определение – минеральный агрегат, являющийся продуктом естественных процессов Это определения включает мантийные породы (гранатовые лерцолиты, коэситовые эклогиты); лунные породы (базальты, анортозиты, феррогаббро); метеориты и другие

Метасоматические Метаморфические Магматические Осадочные

Под магматическими горными породами предлагается понимать естественные ассоциации минералов, минералов и вулканического стекла или только стекла, образовавшихся при застывании или кристаллизации магматических расплавов

Первобытный человек первый петрограф

Использование гранита и базальта древними людьми

Стоунхэндж, Англия - гранодиориты

Львиные ворота, Микены Диориты

Афинский акрополь

Французский учебник по петрографии 1887 г Учебник петрографии Г. Розенбуша 1898 -1922 гг

Учебник В. И. Лучицкого 1949 г Учебник А. Н. Заварицкого 1956 г.

Учебник МГУ- 2000 г Международная классификация 1997 г.

XIX век • Российская петрографическая школа: • А. А. Иностранцев, А. П. Карпинский, И. В. Мушкетов; • Германская петрографическая школа: • Розенбуш, Циркель; • Французкая петрографическая школа: • Фуке, Мишель-Леви, Лакруа; • Английская петрографическая школа: • Тилль

XX век • Российская петрографическая школа: • Ф. Ю. Левинсон-Лессинг, Е. С. Федоров, В. И. Лучицкий, А. Н. Заварицкий, В. Н. Лодочников, Д. С. Коржинский В. С. Соболев, • Германская петрографическая школа: • Г. Розенбуш, Ниггли, Гольдшмидт • Американская петрографическая школа: • Боуэн, Вашингтон, Кросс, Иддингтон, Пирсон • Французкая петрографическая школа: • Лакруа, Дьюпарк, Ле Ба; • Английская петрографическая школа: • Харкер,

Часть 1 Кристаллооптика проходящего света Свет

1. 1. Свет

Светом называется электромагнитные волны, которые регистрируются сетчаткой глаза. Длина таких волн в вакууме лежит в интервале от 380 mμ (фиолетовый) до 780 mμ (красный). Белый свет представляет собой смесь световых колебаний всего спектра видимых волн. (NB надо иметь в виду, что человеческий глаз это своеобразный прибор для регистрации электромагнитных колебаний. ) Он индивидуальный для разных людей, не только имеющих отклонения, например дальтонизм. У фотокамер чувствительность к различным областям спектра бывает разной, поэтому возникают другие окраски, отличные от окрасок, которые видит человек. Свет, обладающий одной длиной волны, называется монохроматическим.

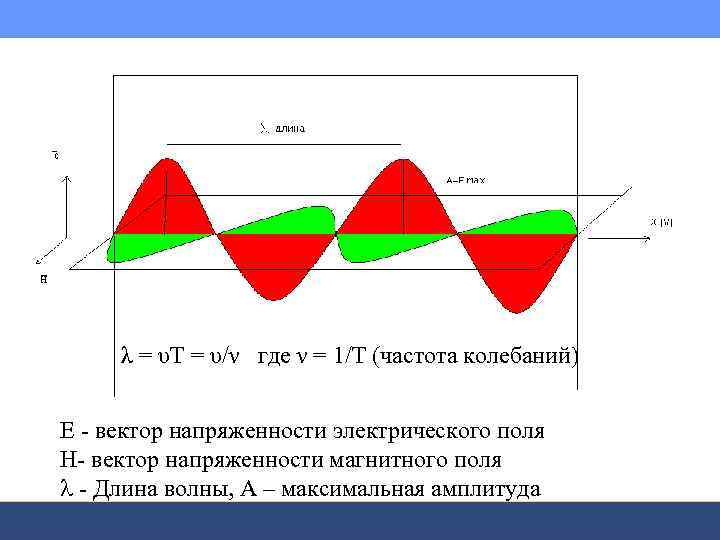λ = υΤ = υ/ν где ν = 1/Т (частота колебаний) Е - вектор напряженности электрического поля H- вектор напряженности магнитного поля - Длина волны, А – максимальная амплитуда

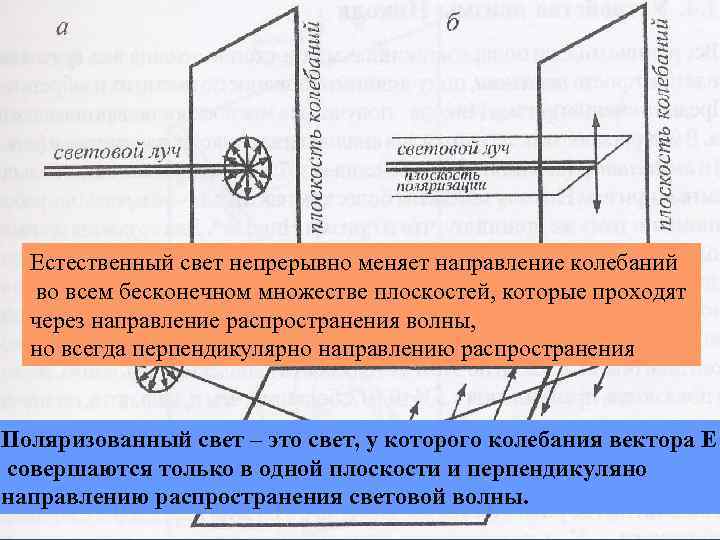Естественный свет непрерывно меняет направление колебаний во всем бесконечном множестве плоскостей, которые проходят через направление распространения волны, но всегда перпендикулярно направлению распространения Поляризованный свет – это свет, у которого колебания вектора Е совершаются только в одной плоскости и перпендикуляно направлению распространения световой волны.

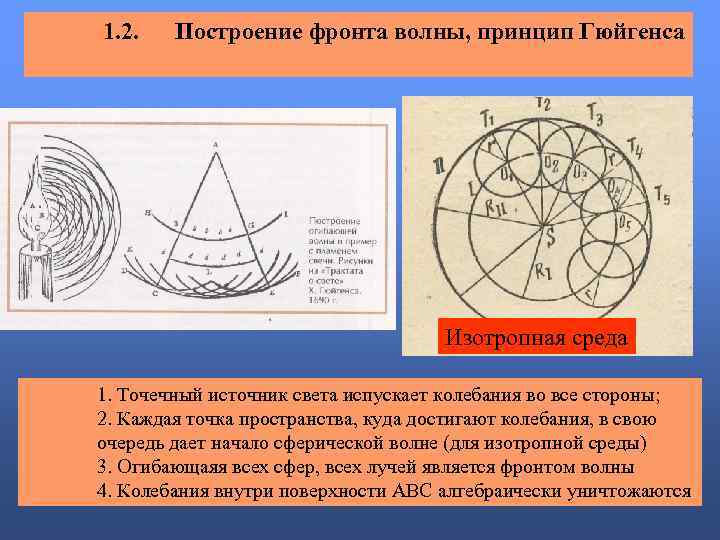1. 2. Построение фронта волны, принцип Гюйгенса Изотропная среда 1. Точечный источник света испускает колебания во все стороны; 2. Каждая точка пространства, куда достигают колебания, в свою очередь дает начало сферической волне (для изотропной среды) 3. Огибающаяя всех сфер, всех лучей является фронтом волны 4. Колебания внутри поверхности ABC алгебраически уничтожаются

1. 3. Показатель преломления света 1 2 1 2 υ1 = λ 1ν; υ2 = λ 2ν; υ1 / λ 1 = υ2 / λ 2 λ 1 = λ 2* υ1/ υ2 Величина υ1/ υ2 = N – относительный показатель преломления второй среды относительно первой. Скорость уменьшается – показатель преломления увеличивается. n = υо/ υ = с/ υ (абсолютный показатель преломления относительно вакуума)

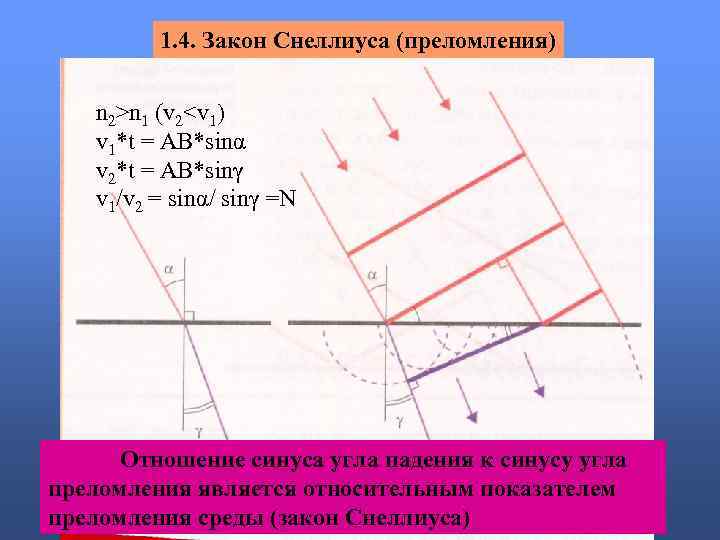1. 4. Закон Снеллиуса (преломления) n 2>n 1 (v 2

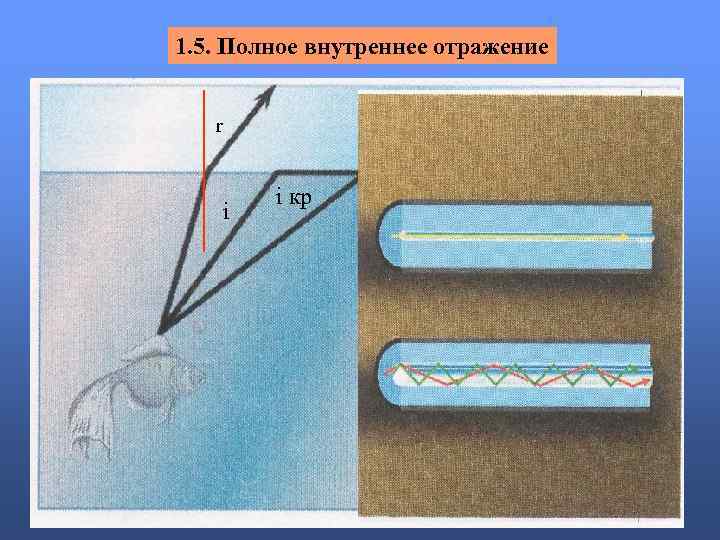1. 5. Полное внутреннее отражение r n 1 i i кр n 2 Sin i / Sin r = N при i кр, r = /2 Sin i кр = N

Рельеф, шагрень КПШ II группа Кварц IV группа