Peter Liljedahl Teaching to the New 10 C

Peter Liljedahl Teaching to the New 10 C Curriculum

Introduction – a difficult task 2

Overview – a plan for the day The NEW curriculum – lessons learned from January BREAK Linking ACTIVITY to the CURRICULUM LUNCH Linking the CURRICULUM to ACTIVITY BREAK Implementation and beyond: HOW DO WE KNOW IT IS WORKING and WHAT NEXT? 3

Activity #1 How tall is Connor? 4

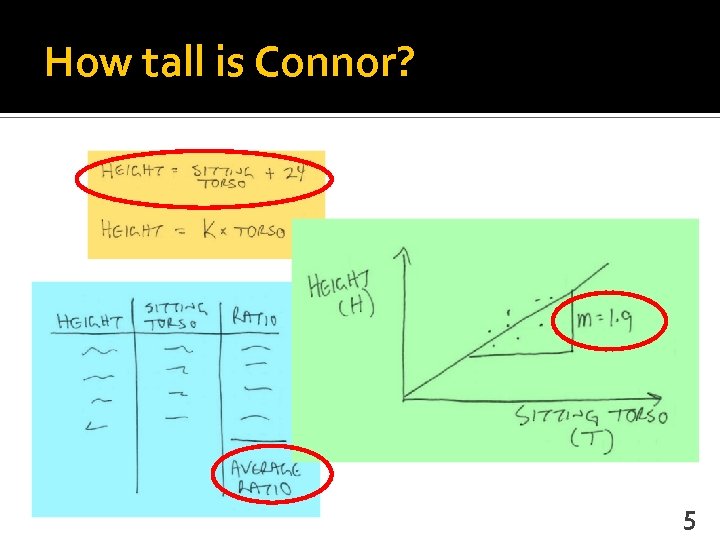How tall is Connor? 5

Linking ACTIVITY to CURRICULUM 6

Learning Outcomes – pg. 19 1. Solve problems that involve linear measurement, using: • SI and imperial units of measure • estimation strategies • measurement strategies. 2. Apply proportional reasoning to problems that involve conversions between SI and imperial units of measure. 7

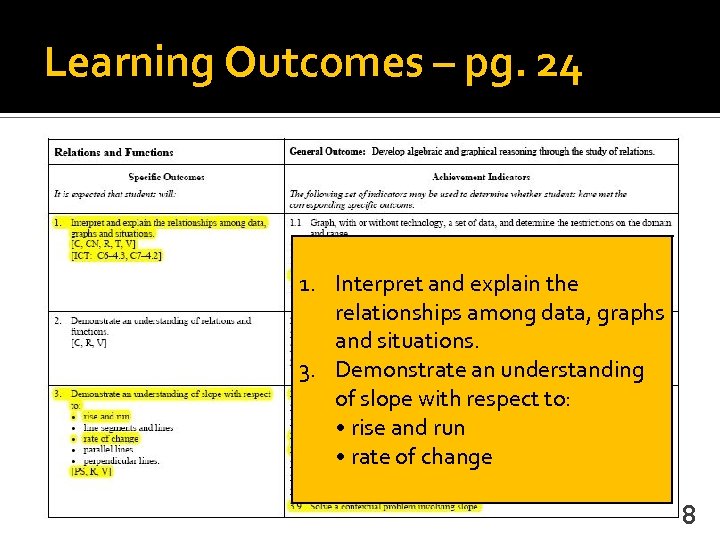Learning Outcomes – pg. 24 1. Interpret and explain the relationships among data, graphs and situations. 3. Demonstrate an understanding of slope with respect to: • rise and run • rate of change 8

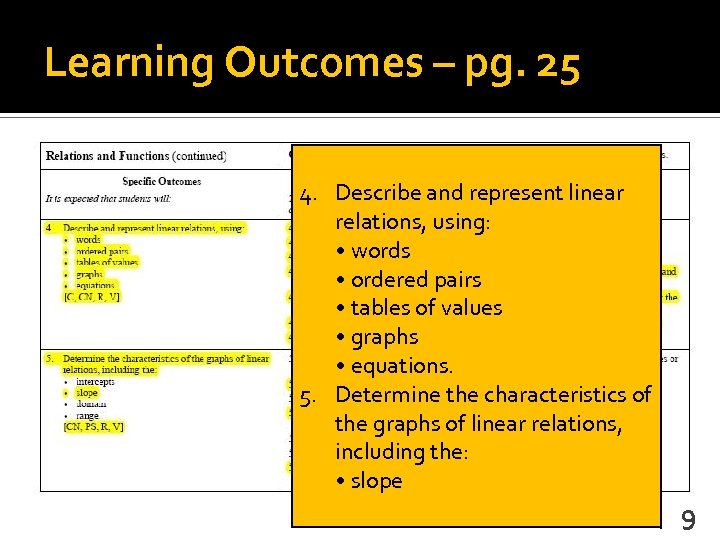Learning Outcomes – pg. 25 4. Describe and represent linear relations, using: • words • ordered pairs • tables of values • graphs • equations. 5. Determine the characteristics of the graphs of linear relations, including the: • slope 9

Mathematical Processes – pg. 6 Students MUST encounter these processes regularly in a mathematics program in order to achieve the goals of mathematics education. All seven processes SHOULD be used in the teaching and learning of mathematics. Each specific outcome includes a list of relevant mathematical processes. THE IDENTIFIED PROCESSES ARE TO BE USED AS A PRIMARY FOCUS OF INSTRUCTION AND ASSESSMENT. 10

Nature of Mathematics – pg. 10 Mathematics is one way of understanding, interpreting and describing our world. There a number of characteristics that define the nature of mathematics, including change, constancy, number sense, patterns, relationships, spatial sense and uncertainty. 11

Goals for Students – pg. 4 Mathematics education must prepare students to use mathematics confidently to solve problems. 12

The New Curriculum Still about: specific outcomes achievement indicators CONTEXT Also about: goals for students mathematical processes nature of mathematics CONTENT 13

Local Discussion What is the value AND feasibility in considering both the specific outcomes and the front matter (goals for students, mathematical processes, nature of mathematics) within our teaching? What are the consequences of not doing so? 15 minutes 14

Question & Answer finish at 10: 30 15

BREAK start again at 10: 45 16

Activity #2 A boy has $80 to buy 100 budgies. Blue budgies cost $3 each, green budgies cost $2 each, and yellow budgies cost $0. 50 each. If he want to ensure that he has at least one budgie of each colour, how many of each colour does he need to buy? Is there more than one answer? How do you know you have ALL the solution? 17

How many budgies? 18

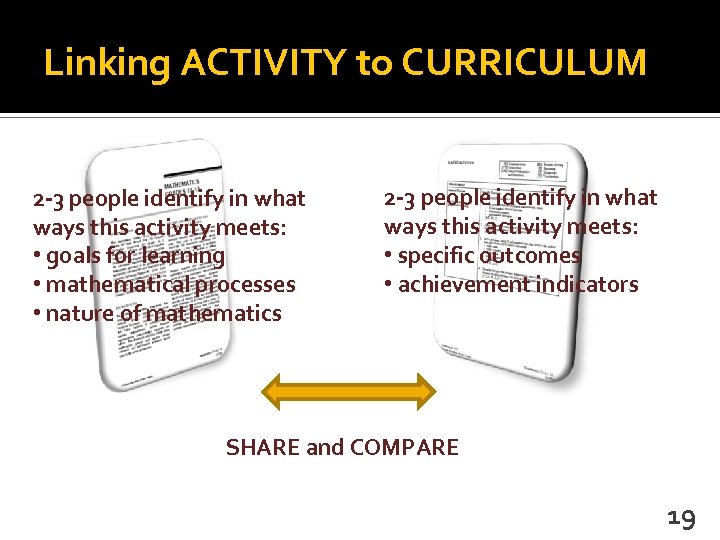Linking ACTIVITY to CURRICULUM 2 -3 people identify in what ways this activity meets: • goals for learning • mathematical processes • nature of mathematics 2 -3 people identify in what ways this activity meets: • specific outcomes • achievement indicators SHARE and COMPARE 19

What is attainable? How many budgies? MATHEMATICAL THINKING 20

Building a culture of THINKING START giving thinking questions using group work randomizing groups using vertical work surfaces talking about thinking strategies (different from solution strategies) assessing thinking evaluating what you value STOP / REDUCE answering stop thinking questions levelling thinking that a lesson is about generating notes assuming that students can't stop emphasizing the use (and creation) of prerequisite knowledge using assessment as a stick 21

Building a culture of THINKING WATCH THE BUILDING A CULTURE OF THINKING WEBINAR! start on day 1 6 consecutive tasks non-curricular no pre-requisite knowledge needed interesting random groups working on feet take pictures 22

Local Discussion How do we live with the possibility that some of these activities bring together curriculum from many different topics within 10 C? 15 minutes 23

Question & Answer finish at 12: 15 24

LUNCH start again at 1: 00 25

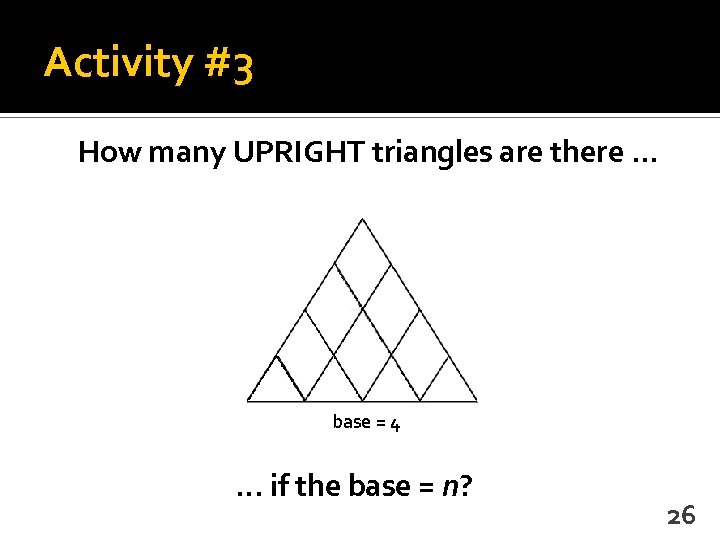Activity #3 How many UPRIGHT triangles are there. . . base = 4 . . . if the base = n? 26

How many UPRIGHT triangles? base size 1 = 10: base size 2 = 6: base size 3 = 3: base size 4 = 1: 1+2+3+4 1+2+3 1+2 1 triangular numbers # of triangles = the sum of the first n triangular #'s 27

How many UPRIGHT triangles? tn = 1 + 2 + 3 +. . . + n (triangular # n) tn + tn-1 = sn (square # n) 28

How many UPRIGHT triangles? base size 1 = 10: base size 2 = 6: base size 3 = 3: base size 4 = 1: 1+2+3+4 1+2+3 1+2 1 triangular numbers # of triangles = the sum of the first n triangular #'s 29

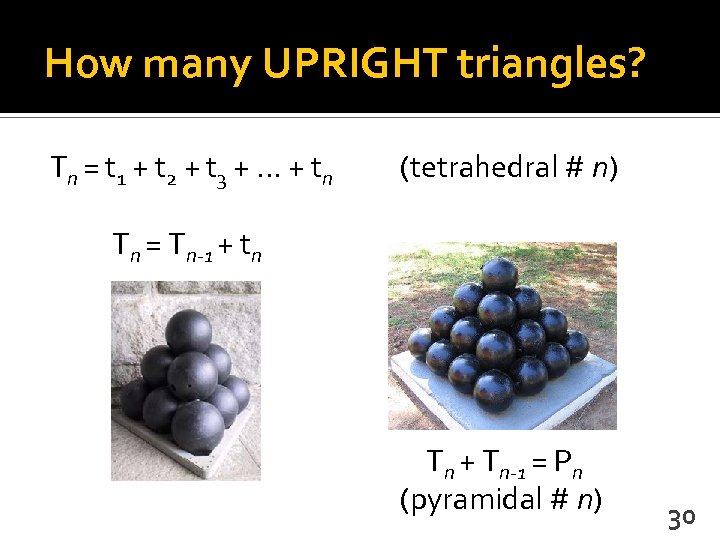How many UPRIGHT triangles? Tn = t 1 + t 2 + t 3 +. . . + tn (tetrahedral # n) Tn = Tn-1 + tn Tn + Tn-1 = Pn (pyramidal # n) 30

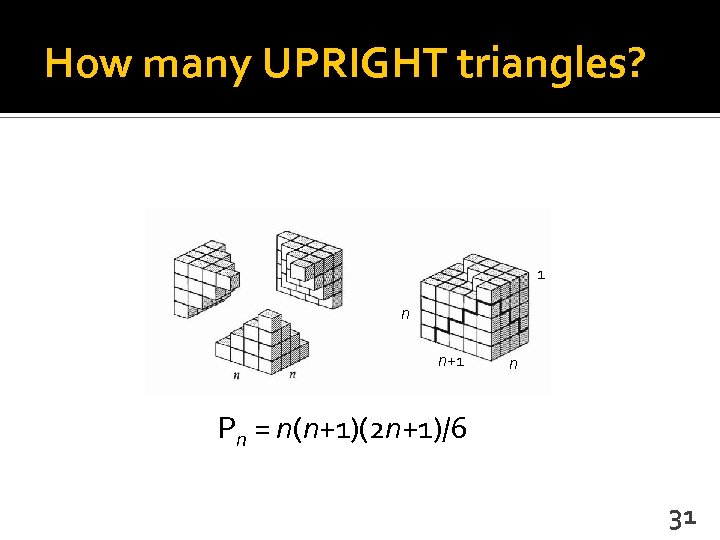How many UPRIGHT triangles? 1 n n+1 n Pn = n(n+1)(2 n+1)/6 31

How many UPRIGHT triangles? Tn = Tn-1 + tn → Tn-1 = Tn - tn Tn + Tn-1 = Pn → Tn + Tn - tn = Pn → 2 Tn - tn = Pn Pn = n(n+1)(2 n+1)/6 2 Tn – n(n+1)/2 = n(n+1)(2 n+1)/6 SHAZAM! Tn = n(n+1)(n+2)/6 32

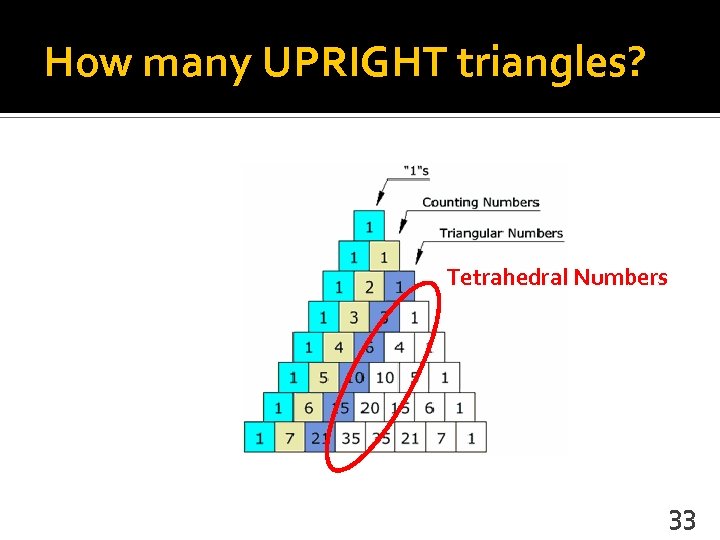How many UPRIGHT triangles? Tetrahedral Numbers 33

Linking CURRICULUM to ACTIVITY Where did this question come from? Where do I use it? the exercises intended for the end of a lesson N O S Sown? Do the students figure out the problem on. E their L N Do they struggle with it? W O So, why do it? D E ID S P U at the beginning of the lesson most figure it out to some level – few to the final formula definitely they learn from their struggles my lesson on it has more meaning to them my lesson is more about formalizing the learning that has already happened it is normal within my classroom 34

Upside Down Lesson – 10 C review: sin is the y-coordinate cos is the x-coordinate ask: If sin t = 0. 5, 0 o < t ≤ 360 o, find t. 35

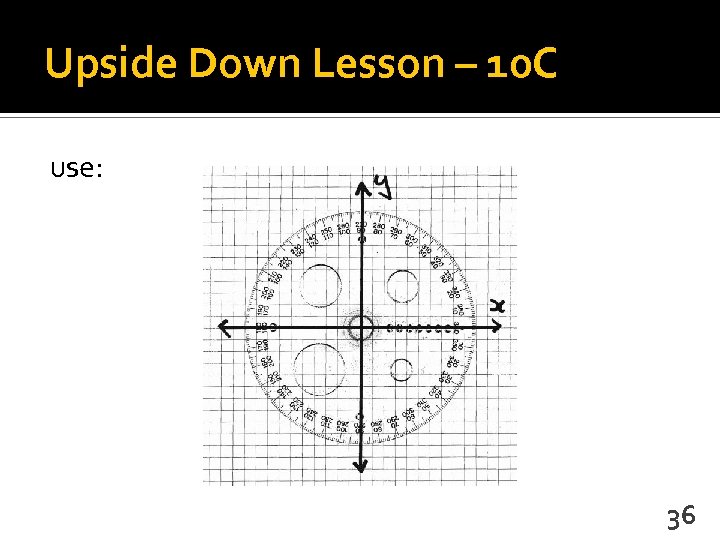Upside Down Lesson – 10 C use: 36

Upside Down Lesson – 10 C try: 2. If sin t = -0. 8, 0 o < t ≤ 360 o, find t. 3. If sin t = 1. 1, 0 o < t ≤ 360 o, find t. 4. If cos t = 0. 5, 0 o < t ≤ 360 o, find t. 5. If cos t = -0. 65, 0 o < t ≤ 360 o, find t. 6. If cos t = 1. 0, 0 o < t ≤ 360 o, find t. 7. If sin t = 0. 7, 0 o < t ≤ 720 o, find t. 8. If tan t = 1, 0 o < t ≤ 360 o, find t. 9. If tan t = -0. 5, 0 o < t ≤ 360 o, find t. 37

Local Discussion What are YOUR challenges in making a rich task out of something as simple as: If sin t = 0. 5, 0 o < t ≤ 360 o, find t. 15 minutes 38

Question & Answer finish at 2: 30 39

BREAK start again at 2: 45 40

How will we know its working? Your behaviour on the tasks – positive • engaged • found solutions • shared • helped • persevered • intrinsic motivation • self selected audience • my obvious charm • my careful selection of the task • my introduction of the task • your trust in me 41

How will we know its working? Your behaviour on the tasks – negative • never engaged • bored • tried but gave up • checked email • socialized • waited • left • lack of intrinsic motivation • inherent anxiety • fatigue • distracted • inappropriate task • wrong set-up • too much/little time • impression I will give answer 42

How will we know its working? Your behaviour on the tasks – a priori • didn't come • came late • sat in the back • sat alone • end of year • coaching • report cards • easily accessible chairs • not Dan Brownesque enough • wrong title • wrong topic 43

How will we know its working? Different interpretations of behaviours: intrinsic characteristics (you) immediate influence (me) contextual influence (the day) outside influence (life) 44

How will we know its working? Different interpretations of behaviours: intrinsic characteristics (you) me as speaker contextual influence (the day) outside influence (life) I would have a source of constant feedback! 45

How will we know its working? Use the mirror that is your classroom: students are sensible student behaviour is sensible (at some scale) student behaviour is a sensible reflection of our teaching look for thinking look for discussion look for engagement look for enjoyment always remember the soccer pitch 46

Local Discussion What will you do to prepare for teaching 10 C in September? 15 minutes 47

Question & Answer finish at 3: 25 48

Final Word Everything I have told you is guaranteed to fail unless YOU think it is important enough to make it work! This is not a PANACEA! There are other dragons to slay (assessment, didactics, notes, practice, review)! You will enjoy teaching in a THINKING classroom! Your students will enjoy THINKING! Your students will LEARN! 49

Thank You liljedahl@sfu. ca finish at 3: 30 50