Первоначальное ознакомление с пакетами прикладных программ используемых для

Первоначальное ознакомление с пакетами прикладных программ, используемых для изучения механизмов химических реакций. Составление Z-матриц для простейших молекул, оптимизация их геометрии. Проведение первых расчетов на ЭВМ и анализ полученных результатов 1

Этапы выполнения квантовохимического исследования • постановка задачи исследования механизма реакции, куда входит поиск литературы по заданной тематике, выбор метода расчета и т. д. ; • оптимизация структур реагентов и продуктов, расчет их энтальпий образования, а также энтальпии реакции; • поиск переходного состояния, идентификация ПС (наличие одной отрицательной моды в матрице вторых производных); • • доказательство принадлежности ПС исследуемому процессу; расчет термодинамических параметров реакции – энтальпии активации, энергии активации, энтропии активации и т. д. ; • выводы о возможности или невозможности протекания исследуемого процесса. 2

Ø Всякое химическое изменение молекулярной системы состоит в изменении взаимного расположения составляющих ее атомов. Чтобы предсказать направление и скорость такого изменения, надо знать зависимость энергии системы Е от взаимного расположения ядер. Эта зависимость называется поверхностью потенциальной энергии (ППЭ). 3

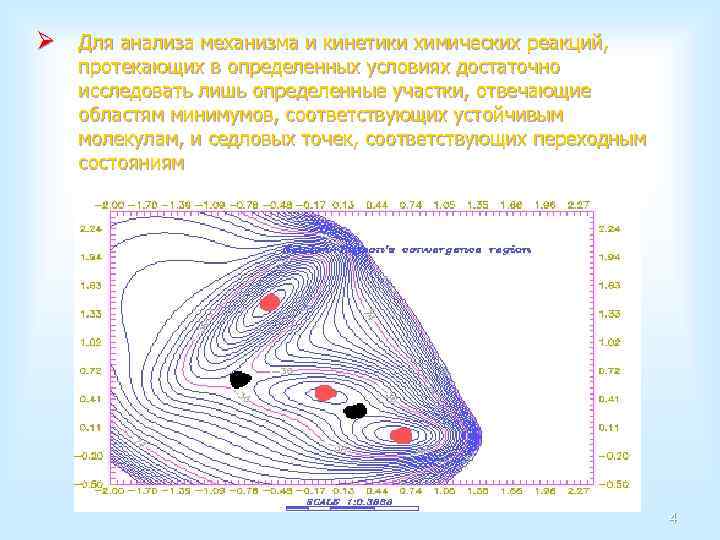Ø Для анализа механизма и кинетики химических реакций, протекающих в определенных условиях достаточно исследовать лишь определенные участки, отвечающие областям минимумов, соответствующих устойчивым молекулам, и седловых точек, соответствующих переходным состояниям 4

Для любой критической точки поверхности потенциальной энергии значение производных (градиент) по каждой независимой координате ядер qi равны нулю, т. е. Расчет вторых производных энергии по всем координатам позволяет охарактеризовать природу экстремальной точки (минимум, максимум и т. д. ). В общем виде набор вторых производных энергии образует матрицу (гессиан) H: 5

Поиск минимумов на поверхности потенциальной энергии Если силовые константы нормальных колебаний системы, которым соответствуют значения матрицы Гессе (Н), имеют положительные значения, то любое смещение из этой области поверхности потенциальной энергии ведет к повышению энергии системы. Эта точка соответствует минимуму, т. е. устойчивым структурам соединений и интермедиатов, не подверженным самопроизвольному распаду или изомеризации и принципиально доступным для экспериментального наблюдения. 6

Поиск минимумов на поверхности потенциальной энергии Процесс минимизации представляет собой итерационную процедуру, продолжающуюся до достижения некоторых критериев сходимости (КС). Время расчета зависит от точности задания начальной геометрии системы. Наиболее простой задачей является выбор начальной геометрии для поиска минимума. В этом случае длины связи, углы и двугранные углы берутся, как правило, из экспериментальных данных или значений, полученных в предыдущих расчетах другими методами. Для любой квантово-химической программы геометрию необходимо задавать строго в определенном виде. Ввод исходной геометрии в Gaussian может производится тремя способами: üв декартовых координатах. Этот способ достаточно труден для восприятия в декартовых координатах. человеком и чаще всего задается с помощью программ визуализации, таких, например, как Chem 3 D, Gauss. Veiw, Hyper. Chem, Chem. Craft и др. ; üв виде z-матриц. Этот способ наиболее распространен, более нагляден и в виде z-матриц. позволяет задавать или вносить изменения в геометрию молекул как с помощью, так и не прибегая к определенным программам визуализации; üв смешанном варианте, но такой способ применяется крайне редко. в смешанном варианте 7

Составление z-матриц атомов и простейших молекул z-Матрица молекулы состоит из двух частей – символьной части и части, содержащей значения переменных: H (символьная часть) H 1 R 2 Variables: (часть, задающая значения R 2 = 0. 9 переменным) 8

Составление z-матриц атомов и простейших молекул • Задание исходной геометрии в виде z-матрицы начинается с нумерации атомов в молекуле, например, молекула водорода имеет два атома H. Присвоим одному из них номер 1, другому соответственно – 2. • Различают z-матрицы для атомов, двухатомных, трехатомных и n-атомных молекул (где n – четыре и более атомов). 9

z-Матрицы для атома: z-Матрицы для атомов записываются в виде: Символ элемента Здесь символ элемента – это либо химический символ атома, либо его порядковый номер в периодической системе Д. И. Менделеева. Так, например, для атома водорода z-матрица запишется в виде: H 10

z-Матрицы для двухатомной молекулы: Первая строка z-матрицы для двухатомной молекулы имеет такой же вид, что и для атома, а вторая записывается в виде: Символ элемента, 1, R 2 1 – обозначает, что второй элемент в z-матрице образует связь с первым атомом в молекуле, R 2 – длина этой связи. Для молекулы водорода z-матрица будет иметь вид: H H 1 R 2 z-Матрица читается в этом случае так: второй атом H связан с первым атомом H длиной связи R 2. 11

z-Матрицы для трехатомной молекулы: Первые две строки z-матрицы для трехатомной молекулы имеют такой же вид, что и для двухатомной, а третья записывается в виде: Символ элемента, N 1, R 3, N 2, A 3 Здесь N 1 – номер атома в z-матрице, с которым образует связь второй атом (в данном случае это уже может быть как 1 так и 2); R 3 – длина этой связь; N 2 – номер атома в z-матрице, с которым образует текущий атом валентный угол; А 3 – валентный угол. Для молекулы воды H O 1 R 2 H 2 R 3 1 A Она читается так: второй атом O связан с первым атомом H длиной связи R 2; третий атом H связан со вторым атомом O длиной связи R 3 и образует валентный угол A 3 с первым атомом водорода. 12

z-Матрицы для n-атомной молекулы: Первые две строки z-матрицы для n-атомной молекулы, где n равно 4 и более атомов, имеет такой же вид, что и для трехатомной, а четвертая и последующие строки записываются в виде: Символ элемента, N 1, R 4, N 2, A 4, N 3, D 4 Здесь N 1 – номер атома в z-матрице, с которым образует связь второй атом (в данном случае это уже может быть 1, 2 или 3); R 4 – длина этой связь; N 2 – номер атома в z-матрице, с которым образует валентный угол; А 4 – валентный угол; N 3 – номер атома в z-матрице, с которым образует двугранный угол, который определяет пространственное расположение атома относительно опорной тройки атомов в молекуле; D 4 – двугранный угол. Для молекулы метана С H 1 R 2 H 1 R 3 2 A 3 H 1 R 4 3 A 4 2 D 4 H 1 R 5 3 A 5 2 D 5 Она читается так: второй атом H связан с первым атомом С длиной связи R 2; третий атом H связан также с первым атомом С длиной связи R 3 и образует валентный угол A 3 со вторым атомом H; четвертый атом H связан также с первым атомом С длиной связи R 4 и образует валентный угол A 4 с третьим атомом H и расположен относительно плоскости, описываемой двумя атомами H и одним атомом С с номерами 2 3 1, под углом D 4; пятый атом H связан также с первым атомом С длиной связи R 5 и образует валентный угол A 5 с третьим атомом H и расположен относительно плоскости, описываемой двумя атомами H и одним атомом С, под углом D 5. 13

Составление z-матриц атомов и простейших молекул Опорными атомами могут быть только атомы, стоящие в предыдущих строках, т. е. имеющие порядковые номера предыдущих строках в молекуле меньше, чем у описываемого атома. Последующие атомы, т. е. имеющие порядковые номера в молекуле больше, чем у описываемого атома, в качестве опорных использоваться не могут. Это значит, что, например, в строке 4 не должны присутствовать значения Nn со значениями 5, 6 и более. 14

Составление z-матриц молекул После задания описательной части z-матрицы, остается только задать значения длин связей (в ангстремах) и углов (в градусах). Для этого после перечня z-матрицы записывается ключевое слово Variables: и далее в столбец перечисляются значения переменных. Например, для наших молекул H 2, H 2 O, CH 4 полные записи z-матриц будут иметь следующий вид: H 2 H H 1 R 2 Variables: R 2 = 0. 9 H 2 O H O 1 R 2 H 2 R 3 1 A 3 Variables: R 2 = 0. 9 R 3 = 0. 9 A 3 = 103. 7 CH 4 С H 1 R 2 H 1 R 3 2 A 3 H 1 R 4 3 A 4 2 D 4 H 1 R 5 3 A 5 2 D 5 Variables: R 2 = 1. 07 R 3 = 1. 07 R 4 = 1. 07 R 5 = 1. 07 A 3 = 109. 47 A 4 = 109. 47 A 5 = 109. 47 D 4 = 120. 0 D 5 = -120. 0 15

Валентные углы Значение валентного угла должен лежать в пределах от 0 o до 180 o. Для линейных молекул, например, CO 2, валентный угол равен 180 o. Кроме того значение валентного угла может выйти за указанные пределы в процессе оптимизации геометрии молекул, особенно переходных состояний реакции. В этих случаях программа оптимизации будет выдавать ошибку расчета. ? Перенумеровать атомы или добавить в z-матрицу так называемые фиктивные атомы или псевдоатомы. Они обозначаются символами X или XX. Их может быть любое количество. Псевдоатомы используются квантово-химической программой только для описания молекулярной геометрии и не оказывают влияния на результаты расчета. Однако во избежание зацикливаний расчетов геометрические параметры псевдоатомов необходимо задавать константами. 16

Добавление в z-матрицу фиктивных атомов O C 1 R 2 O 2 R 3 1 A 3 Variables: R 2 = 1. 2 R 3 = 1. 2 A 3 = 180. 0 O C 1 R 2 X 2 R 3 1 A 3 O 2 R 4 3 A 4 1 D 4 Variables: R 2 = 1. 2 R 4 = 1. 2 A 4 = 90. 0 D 4 = 180. 0 Constants: R 3 = 2. 15 A 3 = 90. 0 17

Двугранные углы могут лежать в пределах от 0 o до 360 o или от 0 o до -360 o. При этом для атома, находящегося: • в одной плоскости с опорной тройкой атомов в цис-положении к первому атому двугранный угол принимает значение 0 o; • в одной плоскости с опорной тройкой атомов в транс-положении к первому атому – 180 o или -180 o (противоположно направленные углы в молекуле); • перпендикулярно плоскости опорной тройки атомов – 90 o или -90 o, ; • под острым углом к плоскости с опорной тройкой атомов – от 0 o до 90 o или от 0 o до -90 o; • под тупым углом к плоскости с опорной тройкой атомов – от 90 o до 180 o или от -90 o до -180 o. Значения для двугранных углов атомов, находящихся под плоскостью, можно задавать как противоположные значение, т. е. со знаком минус, двугранного угла атома, находящегося над плоскостью опорной тройки атомов. Другой способ задать значение двугранного угла 180 o до 360 o. 18

z-Матрицы с одинаковой описательной частью C N 1 R 2 O 2 R 3 1 A 3 O 2 R 4 1 A 4 3 D 4 H 1 R 5 2 A 5 3 D 5 H 1 R 6 2 A 6 3 D 6 H 1 R 7 2 A 7 3 D 7 Variables: R 2 = 1. 48 R 3 = 1. 31 R 4 = 1. 31 R 5 = 1. 1 R 6 = 1. 1 R 7 = 1. 1 A 3 = 120. 0 A 4 = 120. 0 A 5 = 107. 5 A 6 = 107. 5 A 7 = 107. 5 D 4 = -180. 0 D 5 = -60. 0 D 6 = 60. 0 D 7 = 180. 0 C N 1 R 2 O 2 R 3 1 A 3 O 2 R 4 1 A 4 3 D 4 H 1 R 5 2 A 5 3 D 5 H 1 R 6 2 A 6 3 D 6 H 1 R 7 2 A 7 3 D 7 Variables: R 2 = 2. 36 R 3 = 1. 42 R 4 = 1. 16 R 5 = 1. 09 R 6 = 1. 09 R 7 = 1. 09 A 3 = 33. 4 A 4 = 140. 9 A 5 = 94. 8 A 6 = 94. 8 A 7 = 136. 1 D 4 = 0. 0 D 5 = 120. 0 D 6 = -120. 0 D 7 = 180. 0 19

Входные данные Gaussian. Маршрутные строки в исходных файлах Gaussian %mem=n. Mb %chk=h 2 o. chk %nprocshared=M # PM 3 Opt=(Calc. FC, Max. Cycle=100) Freq SCF=(In. Core, Max. Cycle=500) Trans=Incore (специальный раздел) H 2 O Optimization and Frequency (раздел комментариев) 0 1 H O 1 R 2 H 2 R 3 1 A 3 Variables: R 2 = 0. 9 R 3 = 0. 9 A 3 = 103. 7 (маршрутная строка) (спецификация молекулы) 20

Специальный раздел Строки, начинающиеся с символа %, составляют специальный раздел входного символа % файла программы, который дает Gaussian указания по использованию компьютерных ресурсов, по размещению и наименованию файла контрольных точек, Read-Write файлов и т. д. Наиболее часто используемыми в специальном разделе ключевыми словами являются: • %mem – указывает, какое максимальное количество оперативной памяти (n) mem может использовать Gaussian в ходе расчета. Может задаваться в килобайтах, мегабайтах и т. д. Количество оперативной памяти определяется решаемой задачей и ограничено машинными ресурсами. Пример: %mem=300 Mb; =300 Mb • %chk – указывает расположение и название файла контрольных точек, chk записанный в машинных кодах. Этот файл содержит информацию о геометрии системы в процессе расчета, наборе волновых функций, частотах колебаний и т. д. Он может использоваться для запуска: а) задач с рестарта при безошибочном прерывании расчета (например, отключении света); б) последовательных этапов исследования механизма; в) расчета на более высоком уровне и т. д. Пример: %chk=H 2 O. chk • %nprocshared – указывает, какое количество ядер процессора (M) может использовать Gaussian для распараллеливания расчета. Задается на многоядерных или многопроцессорных машинах и в версиях Gaussian, начиная с 09, для Windows и, начиная с 98, для Linux. Пример: %nprocshared=2 21

Специальный раздел %mem=200 Mb %chk=h 2 o. chk %nprocshared=2 # PM 3 Opt=(Calc. FC, Max. Cycle=100) Freq SCF=(In. Core, Max. Cycle=500) Trans=Incore (специальный раздел) H 2 O Optimization and Frequency (раздел комментариев) 0 1 H O 1 R 2 H 2 R 3 1 A 3 Variables: R 2 = 0. 9 R 3 = 0. 9 A 3 = 103. 7 (маршрутная строка) (спецификация молекулы) 22

Маршрутные строки Сразу за специальным разделом следует так называемая маршрутная строка. Это строки, начинающиеся с символа #, содержат информацию о типе символа # расчета, методе исследования и базисном наборе. Порядок используемых в маршрутной строке ключевых слов не имеет значения. Ключевые слова записываются через пробел, в одну и более строк. При этом в новой строке не обязательно повторять знак #, а признаком окончания маршрутной строки является пустая строка. Существует три типа вывода данных в выходной файл: Существует три типа вывода данных в выходной файл • #N – нормальный уровень печати. Это значение в Gaussian используется по #N умолчанию; • #T – краткий вывод: вывод уменьшен до существенной информации и #T результатов; • #P – генерирует дополнительный вывод. Он наряду с информацией о #P сходимости SCF включает сообщения о времени расчета каждого звена цепочки расчета (link). 23

Маршрутные строки В маршрутной строке обязательной является комбинация метод/базисный набор для неэмпирических и гибридных методов расчета или метод для полуэмпирических и расчетов композиционными методами. В маршрутной строке также должны указываться ключевые слова или директивы, которые указывают на тип расчета. В общем случае они записываются в следующем виде: Директива=(параметр1, параметр2, …) Порядок следования параметров, также как и ключевых слов, не имеет значения. Они могут вообще и не указываться. В этом случае будут использоваться параметры, установленные в Gaussian по умолчанию. Кроме того, если задается только один параметр, то можно опустить скобки. 24

Входные данные Gaussian. Маршрутные строки в исходных файлах Gaussian %mem=200 Mb %chk=h 2 o. chk %nprocshared=2 # PM 3 Opt=(Calc. FC, Max. Cycle=100) Freq Opt SCF=(In. Core, Max. Cycle=500) SCF Trans=Incore Trans (специальный раздел) H 2 O Optimization and Frequency (раздел комментариев) 0 1 H O 1 R 2 H 2 R 3 1 A 3 Variables: R 2 = 0. 9 R 3 = 0. 9 A 3 = 103. 7 (спецификация молекулы) (маршрутная строка) 25

Ключевое слово Opt Директива Opt указывает, что Gaussian необходимо выполнить оптимизацию Opt геометрии. Наиболее часто используемыми параметрами этого ключевого слова являются: Параметры, управляющие расчетом силовых констант: • Calc. FC – силовые константы должны быть вычислены вначале текущего расчета с использованием указанного метода, а на последующих этапах считываться из начального значения (используется в показанном примере); • Calc. All – силовые константы должны вычисляться на каждой итерации Calc. All текущего расчета с использованием указанного метода; • Read. FC – силовые константы должны быть считаны вначале и на Read. FC последующих этапах текущего расчета из Check. Point файла, имя которого указывается в специальном разделе; Параметры, управляющие точностью расчета: • Tight – критерии сходимости уменьшаются в 30 раз относительно Tight установленных по умолчанию, т. е. увеличивается точность расчета в 30 раз; • Very. Tight – критерии сходимости уменьшаются в 300 раз относительно Very. Tight установленных по умолчанию, т. е. увеличивается точность расчета в 300 раз; 26

Ключевое слово Opt Директива Opt указывает, что Gaussian необходимо выполнить оптимизацию Opt геометрии. Наиболее часто используемыми параметрами этого ключевого слова являются: Параметры, задающие поиск переходного состояния: • TS – сокращенное от Transition State – оптимизация переходного состояния; TS • QST 2 или QST 3 – поиск переходного состояния с использованием методов линейного транзита; Параметры, задающие алгоритм оптимизации: • EF – используется алгоритм Бейкера (следование собственному вектору) EF оптимизации единичного вектора вместо стандартного алгоритма Берни. Используется чаще всего при поиске переходного состояния или для частичной оптимизации. Хотя и является значительно более медленным по сравнению с алгоритмом Берни, однако более надежен при поиске переходного состояния, начиная с точки, в которой имеется две или более отрицательного собственного значения в матрице вторых производных. Более подробно поговорим об этом на последующих лабораторных занятиях; • GDIIS – определяет использование модифицированного GDIIS алгоритма, GDIIS который рекомендуется задавать для больших систем, имеющих плоские поверхности потенциальной энергии, а также при оптимизации с повышенной тоностью (Opt=Tight). Для полуэмпирических расчетов этот параметр является параметром по умолчанию; 27

Ключевое слово Opt Директива Opt указывает, что Gaussian необходимо выполнить оптимизацию Opt геометрии. Наиболее часто используемыми параметрами этого ключевого слова являются: Параметры, управляющие количеством итераций, размером шага и перезапуском оптимизации: • Max. Сycle=N – устанавливает количество итераций оптимизации N. В нашем примере установлено максимально возможное число итераций для поиска минимума – N=100; • Max. Step=K – устанавливает максимальный размер шага оптимизации 0. 01 К Бора =K или радиуса. По умолчанию К=30; • Restart – позволяет перезапустить задачу из последней точки прерывании Restart оптимизации, вся информации берется из Check. Point файла, имя которого указывается в специальном разделе. 28

Ключевое слово SCF управляет процедурой самосогласования. Наиболее часто SCF используемыми параметрами этого ключевого слова являются: Параметры, управляющие использованием оперативной памятью компьютера: • In. Core – указывает, что необходимые для процедуры самосогласования интегралы и вторые In. Core производны будут вычисляться в оперативной памяти компьютера, что значительно ускоряет расчеты. Если памяти для выполнения расчета не хватает, то программа эту информацию будет, либо сохранять на диске в специальном файле, либо (если время доступа к диску превышает время пересчета) перевычислять по необходимости; Параметры, управляющие методом сходимости SCF: • DIIS – указывает, что используется метод прямой инверсии в итерационной экстраполяции DIIS поверхности П. Пулай (значение, используемое по умолчанию); • QC – указывает, что используется метод квадратичной сходимости вместо стандартного DIIS. Этот метод значительно надежен, но и значительно медленнее стандартного; • x. QC – выполняет дополнительный расчет SCF=QC в случае, когда SCF первого порядка на x. QC сходится Параметры, управляющие точностью процедуры самосогласования: • Conver=n – устанавливает критерий сходимости SCF 10 -n (по умолчанию n = 8); Параметры, управляющие количеством итераций процедуры самосогласования: • Max. Cycle=N – задает максимальное число итераций самосогласования в N шагов (по умолчанию для DIIS N = 64, для QC – N = 512); • Restart – позволяет перезапустить расчет SCF из Check. Point файла, имя которого Restart указывается в специальном разделе. 29

Ключевое слово Freq Все найденные на ППЭ экстремумы идентифицируются как минимумы или переходные состояния вычислением матрицы вторых производных, частот колебаний молекул и подсчетом числа отрицательных собственных значений (мнимых частот колебаний). Директива Freq как раз и указывает, что после окончания оптимизации Freq геометрии молекулы будет выполняться расчет частот колебаний молекулы, а также ее термодинамических характеристик. Ключевое слово Trans контролирует алгоритм преобразования Trans интегралов. Параметр In. Core для этой директивы указывает, что In. Core выполнять процедуру нужно оперативной памяти компьютера. Ключевое слово No. Symm Отменяет контроль точечной группы симметрии в ходе расчета (если это ключевое слово отсутствует, а точечная группа симметрии меняется, Gaussian выдает ошибку). 30

Ключевое слово Guess может включать параметры: Guess • Read – позволяет считать начальное приближение волновых функций Read из файла Check. Point; • Mix – смешивает на начальном этапе верхнюю занятую и нижнюю Mix свободную молекулярные орбитали, подобно учету конфигурационного взаимодействия 2 x 2; • Always, Mix – смешивает верхнюю занятую и нижнюю свободную Mix молекулярные орбитали на каждой итерации расчета. Ключевое слово Geom в свою очередь может включать параметры: Geom • Check. Point – позволяет считать геометрию молекулы из файла Check. Point; • All. Check – позволяет считать заряд, мультиплетность и геометрию молекулы из файла Check. Point. 31

Раздел комментариев Завершением маршрутной строки является пустая строка, после которой следует раздел комментариев. Это единственный раздел входного файла Gaussian, записываемый в произвольной форме. Здесь можно указать любые текстовые комментарии к расчету (название химического соединения, его симметрию, электронное состояние, цель расчета и т. д. ), при этом количество строк ограничено пятью. Кроме того, язык комментариев должен быть английским, иначе в выходном файле вместо текста будут иероглифы. Признаком завершения этого раздела является пустая строка. 32

Раздел комментариев %mem=200 Mb %chk=h 2 o. chk %nprocshared=2 # PM 3 Opt=(Calc. FC, Max. Cycle=100) Freq SCF=(In. Core, Max. Cycle=500) Trans=Incore (специальный раздел) H 2 O Optimization and Frequency (раздел комментариев) 0 1 H O 1 R 2 H 2 R 3 1 A 3 Variables: R 2 = 0. 9 R 3 = 0. 9 A 3 = 103. 7 (спецификация молекулы) (маршрутная строка) 33

Раздел спецификации молекулы В первой строке раздела спецификации указывается заряд и В первой строке заряд мультиплетность рассматриваемой системы (молекулы, радикала или мультиплетность иона). Записываются они либо через пробел, либо через запятую. При этом положительный заряд записывается целым числом (знак плюс можно не указывать), а отрицательный целым числом со знаком минус, например -2. Мультиплетность вычисляется по формуле: M = 2 S+1, +1 где S – общий спин системы; M –мультиплетность системы. Например, для молекулы заряд будет равен 0, спин равен 0, т. к. все ее молекулы электроны спарены, а мультиплетность – 1. Для радикала, который имеет один неспаренный электрон, первая строка радикала раздела спецификации молекулы примет вид: 0 2, т. е. заряд равен 0 и 0 2 мультиплетность 2. Для триплетного состояния, например, наиболее выгодного для молекулы триплетного состояния O 2, которое имеет два одинаково направленных неспаренных электрона, первая строка раздела спецификации молекулы примет вид: 0 3, т. е. заряд 0 3 равен 0 и мультиплетность 3. Для катион-радикала, который имеет положительный заряд и один катион-радикала неспаренный электрон, первая строка раздела спецификации молекулы 34 примет вид: 1 2, т. е. заряд равен +1 и мультиплетность 2. 1 2

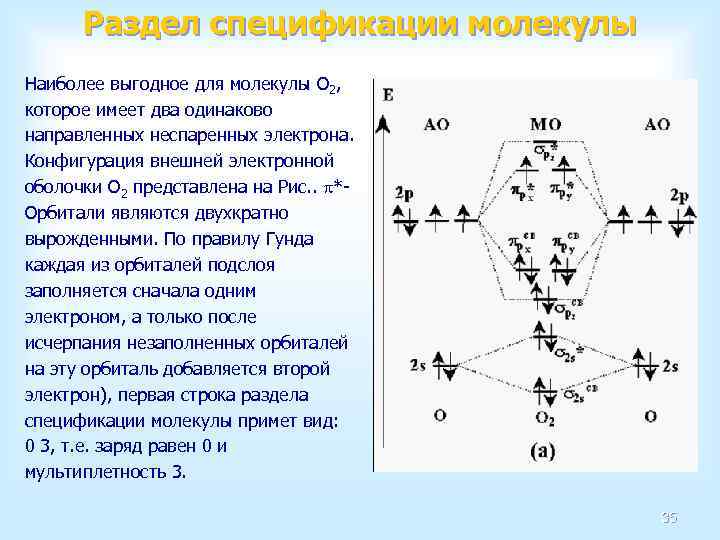Раздел спецификации молекулы Наиболее выгодное для молекулы O 2, которое имеет два одинаково направленных неспаренных электрона. Конфигурация внешней электронной оболочки O 2 представлена на Рис. . *Орбитали являются двухкратно вырожденными. По правилу Гунда каждая из орбиталей подслоя заполняется сначала одним электроном, а только после исчерпания незаполненных орбиталей на эту орбиталь добавляется второй электрон), первая строка раздела спецификации молекулы примет вид: 0 3, т. е. заряд равен 0 и мультиплетность 3. 35

Входные данные Gaussian. Маршрутные строки в исходных файлах Gaussian %mem=200 Mb %chk=h 2 o. chk %nprocshared=2 # PM 3 Opt=(Calc. FC, Max. Cycle=100) Freq SCF=(In. Core, Max. Cycle=500) Trans=Incore (специальный раздел) H 2 O Optimization and Frequency (раздел комментариев) 0 1 H O 1 R 2 H 2 R 3 1 A 3 Variables: R 2 = 0. 9 R 3 = 0. 9 A 3 = 103. 7 (спецификация молекулы) (маршрутная строка) 36

Раздел спецификации молекулы В последующих за зарядом и мультиплетностью строках записываются начальные геометрические параметры молекулы в любой из перечисленной ранее систем координат. После раздела спецификации молекулы и пустой строки могут также присутствовать дополнительные разделы, например, определяющие пользовательские базисные наборы. Об этих разделах подробно можно прочитать в Help Gaussian или другой специальной литературе. 37

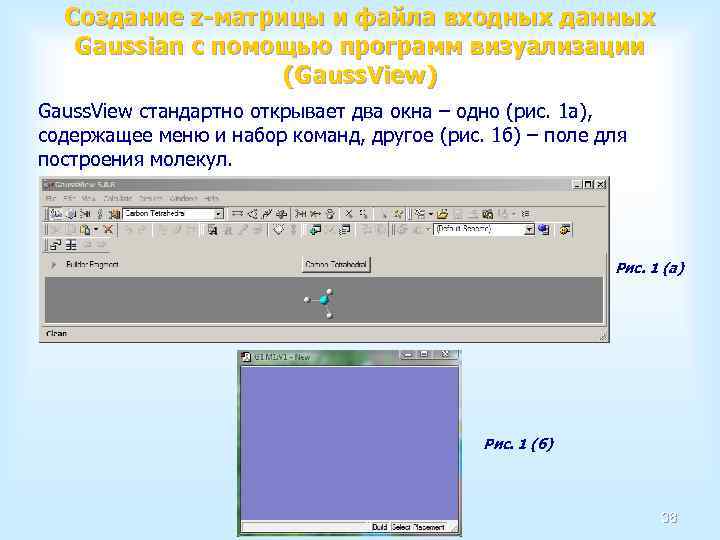Создание z-матрицы и файла входных данных Gaussian с помощью программ визуализации (Gauss. View) Gauss. View стандартно открывает два окна – одно (рис. 1 а), содержащее меню и набор команд, другое (рис. 1 б) – поле для построения молекул. Рис. 1 (а) Рис. 1 (б) 38

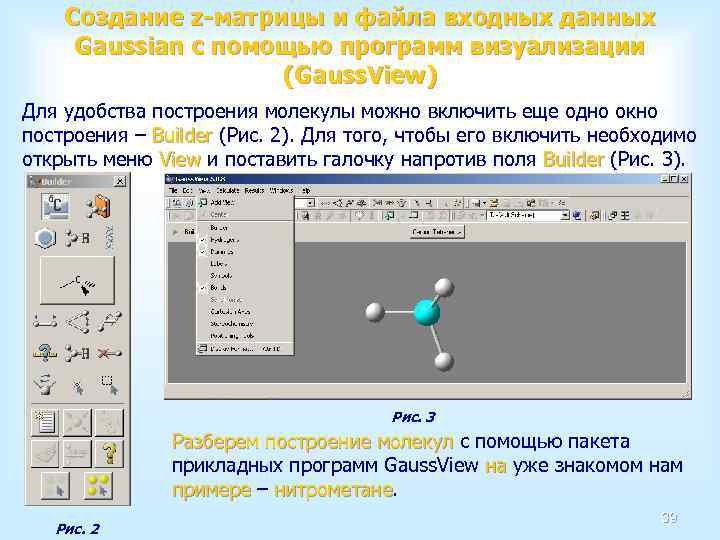Создание z-матрицы и файла входных данных Gaussian с помощью программ визуализации (Gauss. View) Для удобства построения молекулы можно включить еще одно окно построения – Builder (Рис. 2). Для того, чтобы его включить необходимо Builder открыть меню View и поставить галочку напротив поля Builder (Рис. 3). View Builder Рис. 3 Разберем построение молекул с помощью пакета Разберем построение молекул прикладных программ Gauss. View на уже знакомом на примере – нитрометане. примере нитрометане Рис. 2 39

Создание z-матрицы и файла входных данных Gaussian с помощью программ визуализации (Gauss. View) Для выбора элемента периодической системы Д. И. Менделеева откроем окно выбора элемента – Element Fragments (Рис. 4). Вызвать Element его можно двумя способами: 1) нажать кнопку текущего элемента (Carbon Tetrahedral, см. на рис. 1 а) в окне меню; 2) нажать кнопки Carbon Tetrahedral или в окне Builder (Рис. 2). В открывшемся окне Element Builder Fragments необходимо выбрать атом углерода C и его тип – Fragments четырехвалентный. Заметим, что кнопка показывает текущий атом и его тип и при выборе какого-нибудь другого элемента кнопка видоизмениться, например, при выборе атома четырехвалентного азота она примет вид . Рис. 4 После выбора элемента и его типа достаточно щелкнуть мышью по полю построения. При этом в нем появиться молекула метана. 40

Создание z-матрицы и файла входных данных Gaussian с помощью программ визуализации (Gauss. View) Теперь один из атомов водорода нам необходимо заменить на группу NO 2. Конечно это можно сделать последовательным выбором атомов азота и кислорода в окне выбра атома, а можно поступить проще. Но в Gauss. View есть некоторые встроенные стандартные группы, и нитрогруппа является одной из них. Чтобы ее выбрать, необходимо нажать кнопку в окне Builder (Рис. 2). Далее в открывшемся окне Builder R-Group Fragments (Рис. 5) найти группу NO 2, нажать Group Fragments соответствующую кнопку с ее изображением и заменить один из водородов в метане, щелкнув по нему левой кнопкой мыши. Рис. 5 41

Создание z-матрицы и файла входных данных Gaussian с помощью программ визуализации (Gauss. View) Чтобы добавить ароматическую группу или соединение, то в этом случае вместо кнопки в окне Builder нужно было бы нажать Builder кнопку (Рис. 2) и в открывшемся окне Ring Fragments (Рис. 6) Ring Fragments выбрать требуемый циклический заместитель. Рис. 6 42

Создание z-матрицы и файла входных данных Gaussian с помощью программ визуализации (Gauss. View) • При необходимости построенную молекулу можно вращать, удалять или приближать, перемещать относительно поля построения. Выполнить это можно с помощью мыши. Чтобы повращать молекулу достаточно нажать левую кнопку мыши и не отпуская ее перемещать курсор в необходимом направлении. Если выполнить те же действия с правой кнопкой мыши то молекула будет то приближаться (увеличиваться), то удаляться (уменьшаться). А если при удерживании левой кнопки мыши нажать кнопку Shift на клавиатуре, то молекулу можно перемещать влево и вправо, вверх и вниз и т. д. • На молекуле можно показать номера и элементы атомов. Для этого в меню View необходимо поставить галочки напротив полей Labels и Symbol соответственно. 43

Создание z-матрицы и файла входных данных Gaussian с помощью программ визуализации (Gauss. View) Чтобы быстро изменить длину связи, необходимо нажать кнопку в окне Builder (Рис. 2) и затем с помощью левой Builder кнопки мыши выделить два атома, между которыми нужно уменьшить или увеличить расстояние, например, Рис. 7 C и N. При этом откроется диалоговое окно (Рис. 7), которое формально поделено на три секции: 1. Bond Type – управляет визуальным представлением Bond Type типа связи на экране. При этом фактического изменения в расстоянии при смене его типа не происходит. 2. Displacement – содержит два выплывающих списка для атома 1 и атома 2, порядок Displacement которых определяется порядком вашего их выделения в молекуле и показаны на них в квадратных скобках. Эти два списка, одинаковые для двух атомов, позволяют управлять вносимыми изменениями в геометрию соединения. Например, нам надо увеличить длину связи C-N до 2. 5 Å, при этом не изменяя положения остальных атомов. Для этого для атома C, пусть он будет атомом 1, в выпадающем списке выбираем Fixed, а для атома N (соответственно атом 2) – Translate atom. Непосредственное изменение длины связи можно внести перемещая бегунок вправо до значения 2. 5. 3. Позволяет записать новое значение длины связи непосредственно в текстовое Позволяет новое значение длины поле. 44

Создание z-матрицы и файла входных данных Gaussian с помощью программ визуализации (Gauss. View) Валентные и двугранные углы в молекуле изменяются аналогичным способом в соответствующих диалоговых окнах (Рис. 8 и 9 соответственно). В первом случае только необходимо нажать кнопку в окне Builder и затем выделить три атома, а во втором – нажать в окне Builder (Рис. 2) кнопку и выделить четыре атома. Builder Рис. 8 Рис. 9 Для того, чтобы стереть атом требуется нажать кнопку в окне Builder (Рис. 2) и щелкнуть по стираемому атому. 45

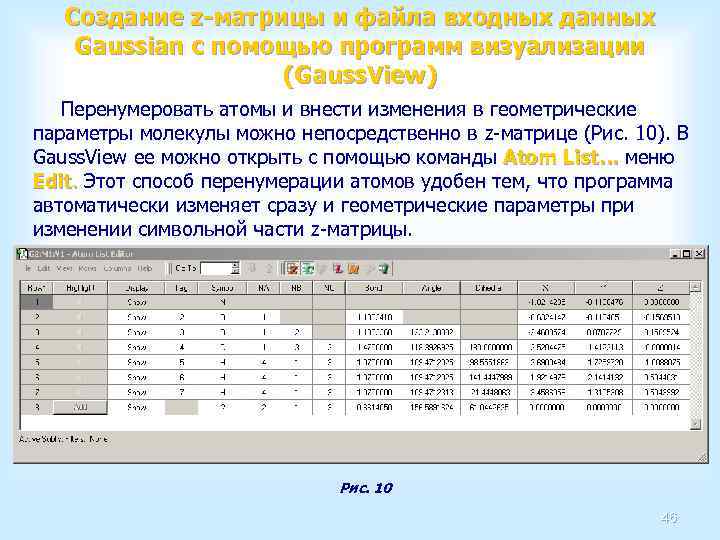Создание z-матрицы и файла входных данных Gaussian с помощью программ визуализации (Gauss. View) Перенумеровать атомы и внести изменения в геометрические параметры молекулы можно непосредственно в z-матрице (Рис. 10). В Gauss. View ее можно открыть с помощью команды Atom List… меню Edit. Этот способ перенумерации атомов удобен тем, что программа автоматически изменяет сразу и геометрические параметры при изменении символьной части z-матрицы. Рис. 10 46

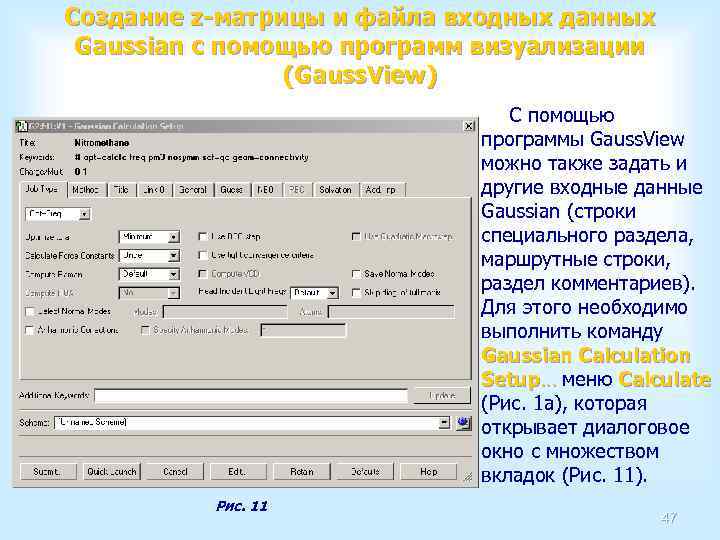Создание z-матрицы и файла входных данных Gaussian с помощью программ визуализации (Gauss. View) C помощью программы Gauss. View можно также задать и другие входные данные Gaussian (строки специального раздела, маршрутные строки, раздел комментариев). Для этого необходимо выполнить команду Gaussian Calculation Setup… меню Calculate (Рис. 1 а), которая открывает диалоговое окно с множеством вкладок (Рис. 11). Рис. 11 47

Окно Gaussian Calculation Setup в Gauss. View • Вкладка Job Type - можно выбрать тип расчета, например, Opt+Freq, что Type означает, что в процессе расчета будет оптимизироваться геометрия и рассчитываться ее частоты колебания и энергетические характеристики. Здесь же выбирается, какую критическую точку на ППЭ нужно найти (минимум, переходное состояние), тип расчета силовых констант, и др. • Вкладка Method - можно выбрать метод расчета, задать заряд и спиновое Method состояние молекулы. • Вкладка Title - вводится строка комментариев. • Вкладка Link 0 - задается специальный раздел. 0 • Вкладка General управляет процессами сходимости, симметрией и др. Другие вкладки мы будем рассматривать по мере необходимости. Соответствующие ключевые слова на каждой вкладке выбираются из ключевые слова выбираются выпадающих списков или, если в этих списках отсутствуют, вводятся в выпадающих списков специальном поле Additional Keywords. При этом набор выбранных специальном поле Keywords параметров показывается в строке Keywords Входные данные Gaussian можно сохранить (для этого необходимо нажать кнопку ) или сразу запустить на расчет (для этого необходимо нажать кнопку ). 48

Создание z-матрицы и файла входных данных Gaussian с помощью программ визуализации (Gauss. View) Существует три варианта сохранения входного файла Gaussian из Gauss. View: 1. Выполняется команда Save… меню File. При этом не вносится никаких изменений в Save… File открывающемся окне сохранения, а лишь записывается имя файла. В этом случае мы получим входной файл Gaussian, содержащий структуру молекулы в декартовых координатах %nprocshared=2 %mem=300 MB %chk=C: G 09 W_3201112nm. chk # opt=calcfc freq pm 3 nosymm scf=qc geom=connectivity Nitromethane 0 1 O -0. 63241474 -0. 11346508 -0. 15695181 O -2. 46805743 0. 87877290 0. 15695235 C -2. 52044755 -1. 41221134 -0. 00000140 H -2. 69004840 -1. 72597199 -1. 00880753 H -1. 92149792 -2. 14141323 0. 50440314 H -3. 45860592 -1. 31053082 0. 50439918 N -1. 82142853 -0. 11904762 0. 0000 1 7 1. 5 2 7 1. 5 3 4 1. 0 5 1. 0 6 1. 0 7 1. 0 4 5 6 7 49

Создание z-матрицы и файла входных данных Gaussian с помощью программ визуализации (Gauss. View) Существует три варианта сохранения входного файла Gaussian из Gauss. View: 2. Выполняется команда Save… меню File, снимается галочка в окне Save File Save… File галочка File в поле Write Cartesians и задается имя файла. В этом случае мы получим входной Cartesians файл Gaussian, содержащий z-матрицу, в которой все геометрические параметры молекулы являются константами %nprocshared=2 %mem=300 MB %chk=C: G 09 W_3201112nm 1. chk # opt=calcfc freq pm 3 nosymm scf=qc geom=connectivity Nitromethane 0 1 O 1 2. 11013178 C 2 2. 29695189 1 62. 65628918 H 3 1. 07000000 2 111. 13158771 1 -91. 75264207 0 H 3 1. 07000000 2 129. 40124233 1 49. 50486709 0 H 3 1. 07000000 2 83. 85787914 1 159. 71530873 0 N 2 1. 19933680 1 28. 39310912 3 0. 0000 0 1 7 1. 5 2 7 1. 5 3 4 1. 0 5 1. 0 6 1. 0 7 1. 0 4 5 6 7 50

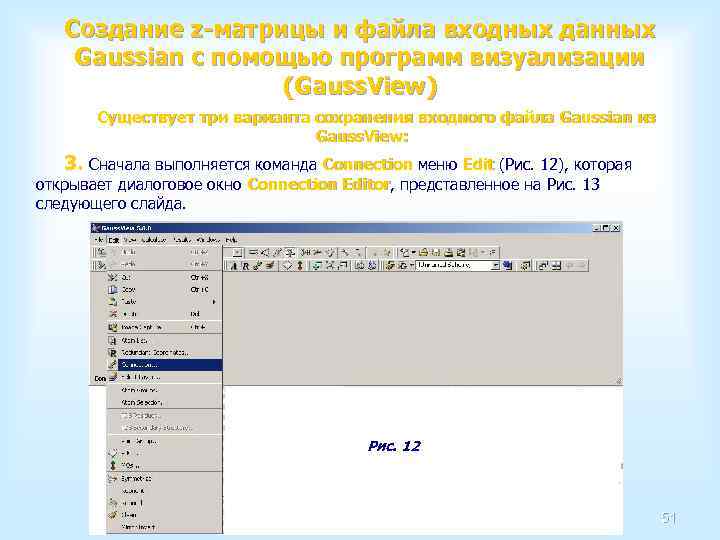Создание z-матрицы и файла входных данных Gaussian с помощью программ визуализации (Gauss. View) Существует три варианта сохранения входного файла Gaussian из Gauss. View: 3. Сначала выполняется команда Connection меню Edit (Рис. 12), которая Connection Edit открывает диалоговое окно Connection Editor, представленное на Рис. 13 Editor следующего слайда. Рис. 12 51

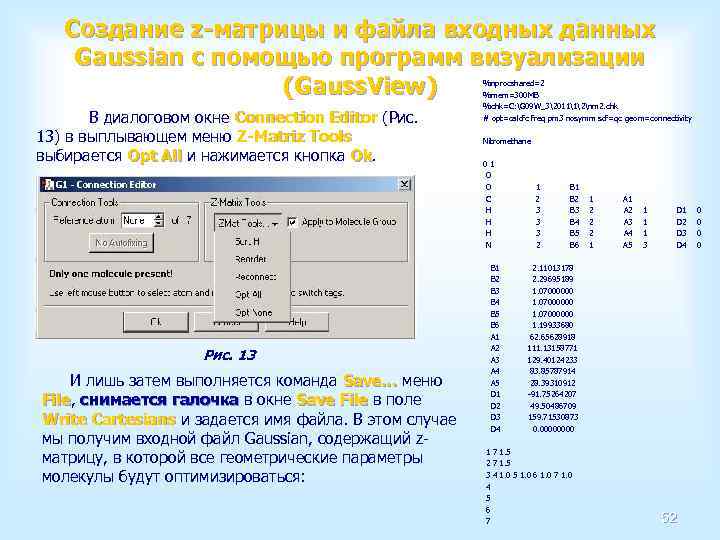Создание z-матрицы и файла входных данных Gaussian с помощью программ визуализации (Gauss. View) В диалоговом окне Connection Editor (Рис. 13) в выплывающем меню Z-Matriz Tools выбирается Opt All и нажимается кнопка Ok. All Ok Рис. 13 И лишь затем выполняется команда Save… меню Save… File, снимается галочка в окне Save File в поле File галочка File Write Cartesians и задается имя файла. В этом случае Cartesians мы получим входной файл Gaussian, содержащий zматрицу, в которой все геометрические параметры молекулы будут оптимизироваться: %nprocshared=2 %mem=300 MB %chk=C: G 09 W_3201112nm 2. chk # opt=calcfc freq pm 3 nosymm scf=qc geom=connectivity Nitromethane 0 1 O 1 B 1 C 2 B 2 1 A 1 H 3 B 3 2 A 2 1 D 1 0 H 3 B 4 2 A 3 1 D 2 0 H 3 B 5 2 A 4 1 D 3 0 N 2 B 6 1 A 5 3 D 4 0 B 1 2. 11013178 B 2 2. 29695189 B 3 1. 07000000 B 4 1. 07000000 B 5 1. 07000000 B 6 1. 19933680 A 1 62. 65628918 A 2 111. 13158771 A 3 129. 40124233 A 4 83. 85787914 A 5 28. 39310912 D 1 -91. 75264207 D 2 49. 50486709 D 3 159. 71530873 D 4 0. 0000 1 7 1. 5 2 7 1. 5 3 4 1. 0 5 1. 0 6 1. 0 7 1. 0 4 5 6 7 52

Создание z-матрицы и файла входных данных Gaussian с помощью программ визуализации (Gauss. View) Сохранять данные следует в понятном для Gaussian текстовом формате с расширением gjf. формате gjf В пакете прикладных программ Gaussian можно запускать задачи по одной (*. gjf) или создавать пакеты последовательно запускаемых gjf задач в виде файлов с расширением bcf, куда записываются bcf названия исходных (*. gjf) и выходных (*. out) файлов. gjf out 53

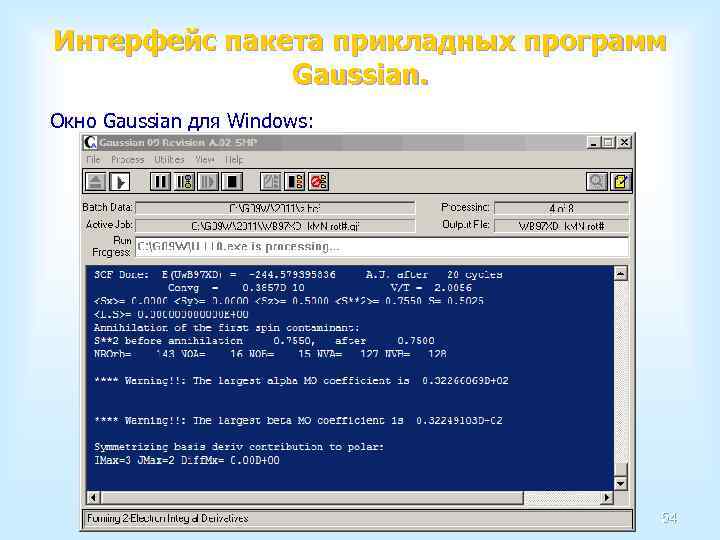Интерфейс пакета прикладных программ Gaussian. Окно Gaussian для Windows: 54

Окно Gaussian для Windows Имеет строку стандартного меню, куда входят: • меню File, содержащее команды, относящиеся к файлам (создание, открытие, File сохранение) и свойствам Gaussian (пути размещения исходных данных, сохранения выходных данных, вида окна и т. д. ); • меню Process, содержащее команды, позволяющие управлять текущими Process процессами или цепочкой процессов, запущенных в Gaussian (начать процесс, поставить на паузу, поставить на паузу следующий link, завершить процесс, убить процесс, завершить пакет расчетных задач, убить пакет расчетных задач); • меню Utilities, содержащее команды, относящиеся к выполнению встроенных Utilities утилит, таких как, например, создание и редактирование файла пакета расчетных задач (batch-файла), конвертирование z-матрицы, конвертирование файлов контрольных точек, полученных в предыдущих версиях программы и др. ; • меню View, содержащее команды, управляющими панелями инструментов, View окнами вывода текущих результатов расчета на экран, строкой текущего действия, а также редактированием и просмотром файла результатов; • меню Help – содержит команды, вызывающие различные виды справки Help Gaussian. 55

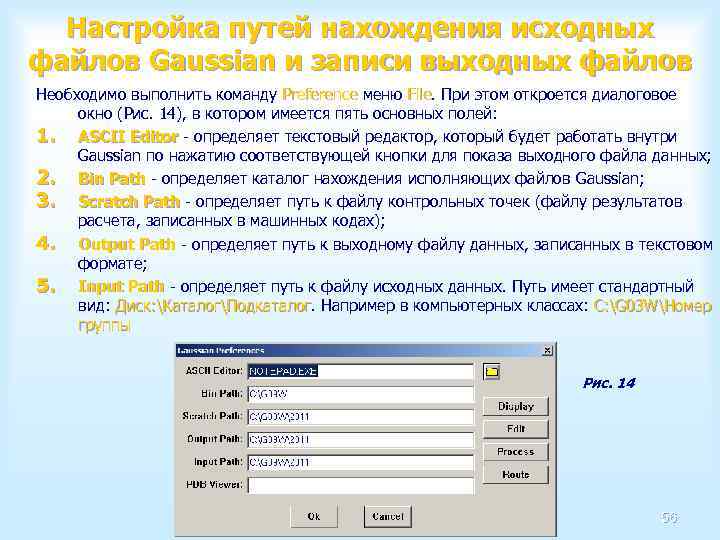Настройка путей нахождения исходных файлов Gaussian и записи выходных файлов Необходимо выполнить команду Preference меню File. При этом откроется диалоговое Preference File окно (Рис. 14), в котором имеется пять основных полей: 1. ASCII Editor - определяет текстовый редактор, который будет работать внутри Editor Gaussian по нажатию соответствующей кнопки для показа выходного файла данных; 2. Bin Path - определяет каталог нахождения исполняющих файлов Gaussian; Path 3. Scratch Path - определяет путь к файлу контрольных точек (файлу результатов Path расчета, записанных в машинных кодах); 4. Output Path - определяет путь к выходному файлу данных, записанных в текстовом Path формате; 5. Input Path - определяет путь к файлу исходных данных. Путь имеет стандартный Path вид: Диск: КаталогПодкаталог. Например в компьютерных классах: C: G 03 WНомер Диск: КаталогПодкаталог группы Рис. 14 56

Панель инструментов Gaussian Кнопки команд меню Process: Process – открытие исходного файла Gaussian; – запуск текущего задания; – поставить текущий расчет на паузу; – поставить на паузу следующий link задачи; – закончить процесс, поставленный на паузу; – убить процесс; – редактировать пакет расчетных задач (batch-файл); – завершить пакет расчетных задач; – убить batch-файл). Две кнопки меню View: View – просмотр файла результатов; – редактирование файла результатов. Эту панель можно убрать с экрана сняв галочку напротив команды Toolbar меню View. Toolbar View 57

Окно Gaussian для Windows Под панелью инструментов располагаются поля, содержащие информацию о текущих заданиях: • Batch Date – о размещении и названии batch-файла; Batch Date • Processing – номер задания из максимального числа задач, записанных в Processing batch-файле (например, 1 of 3); • Active Job – размещение и название текущей задачи (исходного файла Active Job Gaussian); • Output File – название выходного файла с расширением out; Output File • Run Process – размещение и название исполняющего текущую итерацию Run Process расчета (link) файла exe. Далее располагается окно, позволяющее отследить текущие результаты расчета. Это окно можно убрать с экрана сняв галочку напротив команды Processing Output меню View. Processing Output View Внизу окна Gaussian располагается строка, которая расшифровывает текущую итерацию расчета, например, Performing the Initial MO Guess. Эта строка также отключается снятием галочки в меню View напротив команды View Status Bar 58

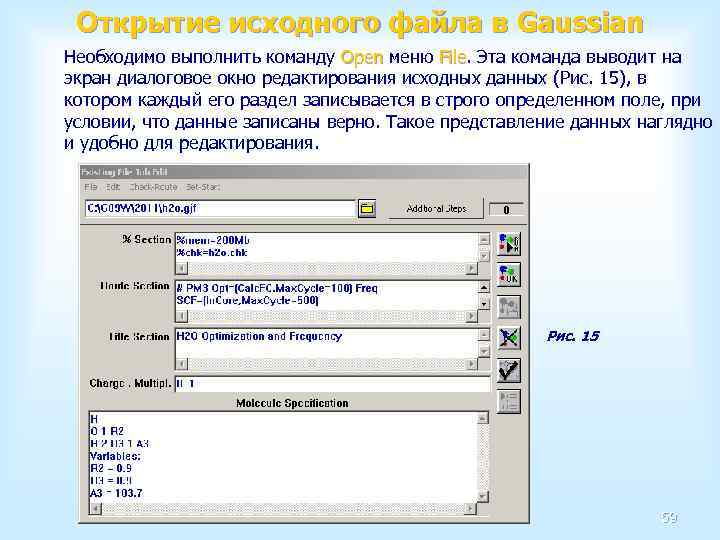Открытие исходного файла в Gaussian Необходимо выполнить команду Open меню File. Эта команда выводит на Open File экран диалоговое окно редактирования исходных данных (Рис. 15), в котором каждый его раздел записывается в строго определенном поле, при условии, что данные записаны верно. Такое представление данных наглядно и удобно для редактирования. Рис. 15 59

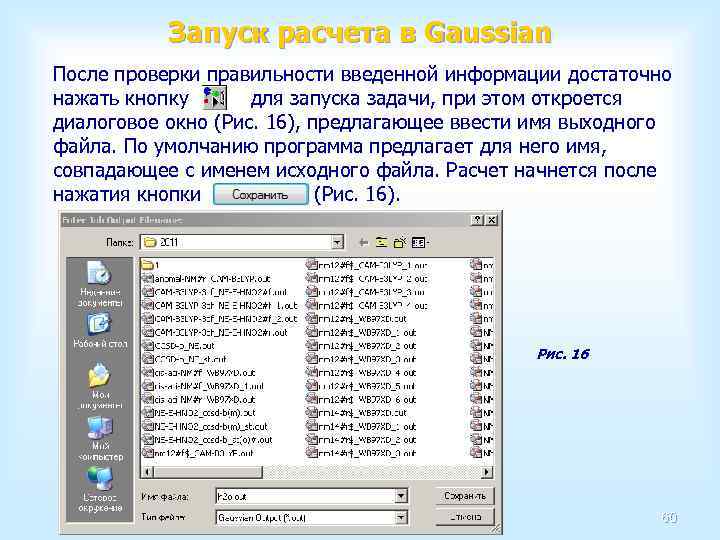Запуск расчета в Gaussian После проверки правильности введенной информации достаточно нажать кнопку для запуска задачи, при этом откроется диалоговое окно (Рис. 16), предлагающее ввести имя выходного файла. По умолчанию программа предлагает для него имя, совпадающее с именем исходного файла. Расчет начнется после нажатия кнопки (Рис. 16). Рис. 16 60

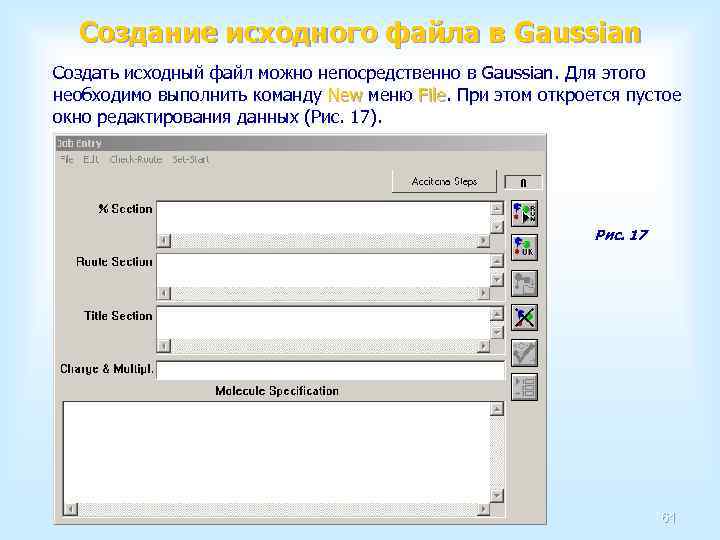Создание исходного файла в Gaussian Создать исходный файл можно непосредственно в Gaussian. Для этого необходимо выполнить команду New меню File. При этом откроется пустое New File окно редактирования данных (Рис. 17). Рис. 17 61

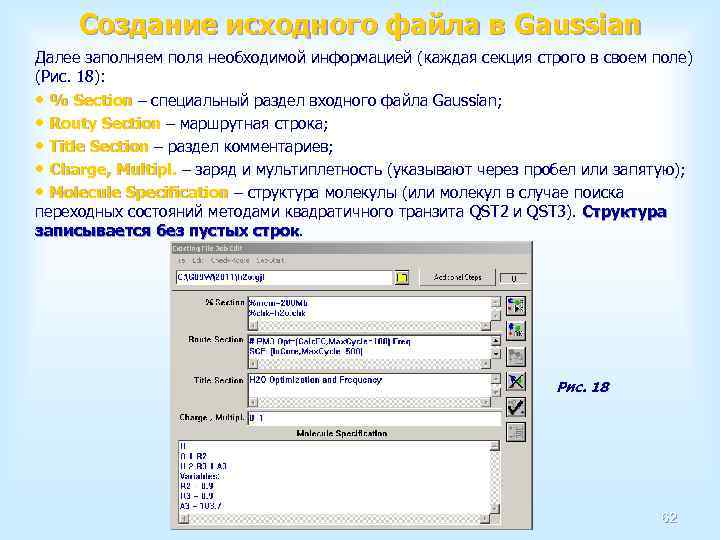Создание исходного файла в Gaussian Далее заполняем поля необходимой информацией (каждая секция строго в своем поле) (Рис. 18): • % Section – специальный раздел входного файла Gaussian; Section • Routу Section – маршрутная строка; Section • Title Section – раздел комментариев; Section • Charge, Multipl. – заряд и мультиплетность (указывают через пробел или запятую); • Molecule Specification – структура молекулы (или молекул в случае поиска Specification переходных состояний методами квадратичного транзита QST 2 и QST 3). Структура записывается без пустых строк. записывается строк Рис. 18 62

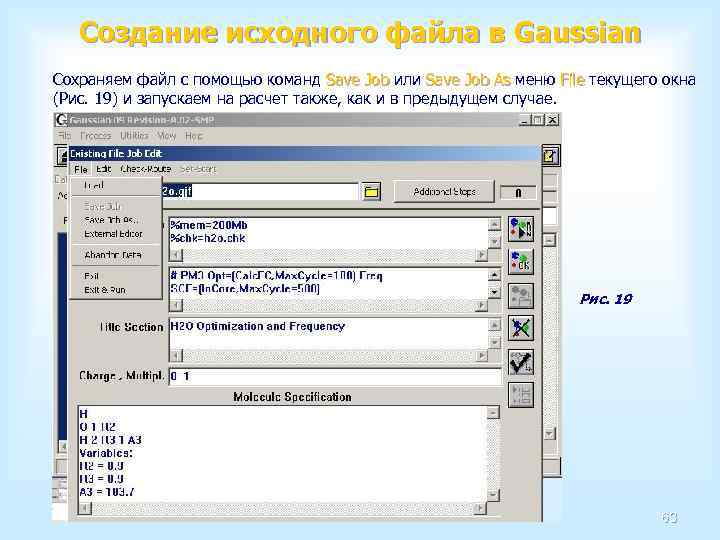Создание исходного файла в Gaussian Сохраняем файл с помощью команд Save Job или Save Job As меню File текущего окна Job As File (Рис. 19) и запускаем на расчет также, как и в предыдущем случае. Рис. 19 63

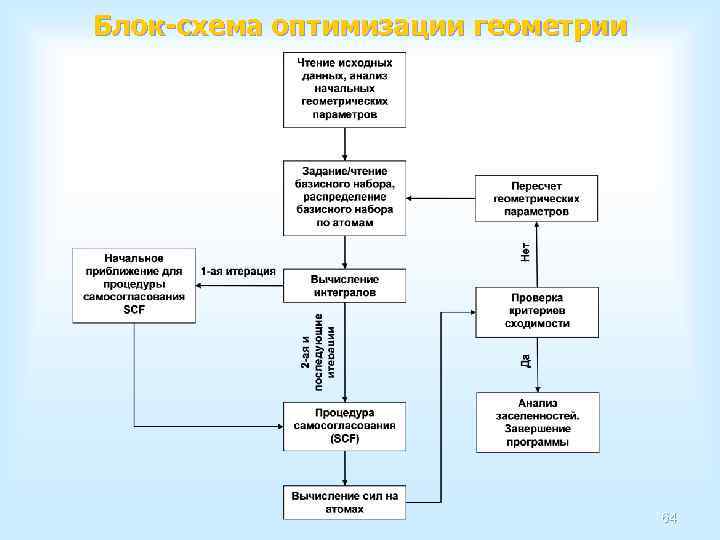Блок-схема оптимизации геометрии 64

Оптимизация геометрии • Процесс расчета в Gaussian собственно начинается после вывода заданных начальных данных, анализа геометрических переменных, распределения базисных наборов по атомам системы и анализа симметрии молекулы. • На каждой итерации выдается следующая информация: используемые изотопы атомов, используемые базисные наборы, типы используемой орбитальной симметрии, количество базисных функций, примитивных гауссианов и электронов и др. • В конце работы процедуры самосогласования на всех этапах оптимизации указываются критерии сходимости и результаты работы процедуры SCF. 65

Критерии сходимости в Gaussian В программе GAUSSIAN используются следующие критерии GAUSSIAN сходимости (КС) (приведены значения, используемые по умолчанию, сходимости в атомных единицах): • градиент энергии (отрицательная сила) должен быть близок к 0 (в градиент энергии отрицательная сила частности максимальный компонент силы должен быть ниже значения 0. 00045 а. е. ); • среднеквадратичное значение силы должно быть близко к 0 (ниже среднеквадратичное значение силы допускаемого значения 0. 0003 а. е. ); • рассчитываемое смещение для следующего шага должно быть рассчитываемое смещение для следующего шага меньше определенного граничного значения 0. 0018 а. е. ; • среднеквадратичное значение смещения для следующего шага должно быть ниже граничного значения 0. 0012 а. е. Эти КС можно легко изменить (увеличить или уменьшить), тем самым изменить точность расчета с помощью некоторого набора «ключевых слов» в «маршрутной строке» исходного файла программы Gaussian. 66

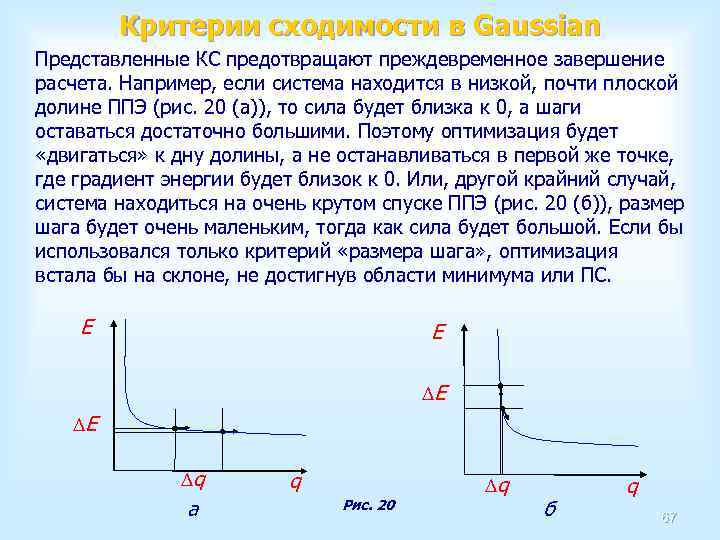Критерии сходимости в Gaussian Представленные КС предотвращают преждевременное завершение расчета. Например, если система находится в низкой, почти плоской долине ППЭ (рис. 20 (а)), то сила будет близка к 0, а шаги оставаться достаточно большими. Поэтому оптимизация будет «двигаться» к дну долины, а не останавливаться в первой же точке, где градиент энергии будет близок к 0. Или, другой крайний случай, система находиться на очень крутом спуске ППЭ (рис. 20 (б)), размер шага будет очень маленьким, тогда как сила будет большой. Если бы использовался только критерий «размера шага» , оптимизация встала бы на склоне, не достигнув области минимума или ПС. E E E E q a q Рис. 20 q б q 67

Критерии сходимости в Gaussian Анализ сходимости оптимизации геометрических параметров молекулы программе представлен следующими строками: Item Value Threshold Converged? Maximum Force 0. 045167 0. 000450 NO RMS Force 0. 015056 0. 000300 NO Maximum Displacement 0. 041996 0. 001800 NO RMS Displacement 0. 014926 0. 001200 NO Здесь в первой колонке перечисляются критерии, во второй – приводятся их значения на данной итерации расчета, в третьей – допустимые значения, в четвертой – анализ сходимости. Понятно, что процедура оптимизации продолжается до тех пор, пока когда все логические переменные в последней колонке не станут равными Yes: Item Value Threshold Converged? Maximum Force 0. 000091 0. 000450 YES RMS Force 0. 000028 0. 000300 YES Maximum Displacement 0. 000268 0. 001800 YES RMS Displacement 0. 000117 0. 001200 YES 68

Выводная информация в Gaussian На начальной и конечной итерациях оптимизации Gaussian выдает дополнительную информацию о рассчитываемой системе, а именно, значения энергий молекулярных орбиталей, распределение электронов по орбиталям, анализ заселенностей по Маликену, эффективные заряды на атомах, спиновые плотности на атомах, мультипольные моменты системы и их компоненты. Полнота этих данных зависит от исследуемой системы и метода расчета. 69

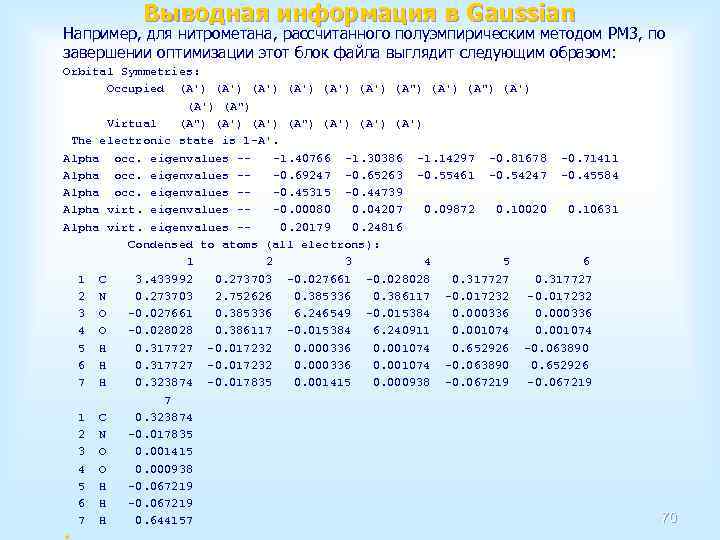Выводная информация в Gaussian Например, для нитрометана, рассчитанного полуэмпирическим методом PM 3, по завершении оптимизации этот блок файла выглядит следующим образом: Orbital Symmetries: Occupied (A') (A') (A") (A') (A") Virtual (A") (A') (A') The electronic state is 1 -A'. Alpha occ. eigenvalues --1. 40766 -1. 30386 -1. 14297 -0. 81678 -0. 71411 Alpha occ. eigenvalues --0. 69247 -0. 65263 -0. 55461 -0. 54247 -0. 45584 Alpha occ. eigenvalues --0. 45315 -0. 44739 Alpha virt. eigenvalues --0. 00080 0. 04207 0. 09872 0. 10020 0. 10631 Alpha virt. eigenvalues -0. 20179 0. 24816 Condensed to atoms (all electrons): 1 2 3 4 5 6 1 C 3. 433992 0. 273703 -0. 027661 -0. 028028 0. 317727 2 N 0. 273703 2. 752626 0. 385336 0. 386117 -0. 017232 3 O -0. 027661 0. 385336 6. 246549 -0. 015384 0. 000336 4 O -0. 028028 0. 386117 -0. 015384 6. 240911 0. 001074 5 H 0. 317727 -0. 017232 0. 000336 0. 001074 0. 652926 -0. 063890 6 H 0. 317727 -0. 017232 0. 000336 0. 001074 -0. 063890 0. 652926 7 H 0. 323874 -0. 017835 0. 001415 0. 000938 -0. 067219 7 1 C 0. 323874 2 N -0. 017835 3 O 0. 001415 4 O 0. 000938 5 H -0. 067219 6 H -0. 067219 7 H 0. 644157 70

Выводная информация в Gaussian Например, для нитрометана, рассчитанного полуэмпирическим методом PM 3, по завершении оптимизации этот блок файла выглядит следующим образом: Total atomic charges: 1 1 C -0. 611332 2 N 1. 254516 3 O -0. 590927 4 O -0. 586701 5 H 0. 176278 6 H 0. 176278 7 H 0. 181889 Sum of Mulliken charges= 0. 00000 Atomic charges with hydrogens summed into heavy atoms: 1 1 C -0. 076888 2 N 1. 254516 3 O -0. 590927 4 O -0. 586701 5 H 0. 000000 6 H 0. 000000 7 H 0. 000000 Sum of Mulliken charges= 0. 00000 71

Расчет частот и колебания и термохимических поправок к полной энергии • Проводится Gaussian как отдельная задача (Freq), которая запускается после выполнения процесса оптимизации геометрии. Следует отметить, что эта процедура также будет работать и без оптимизации, однако в этом случае полученные значения не будут соответствовать критической точки поверхности потенциальной энергии. • Частоты колебания молекул (см-1), число которых равно 3 N-6, где N – число атомов в системе, по сути, представляют собой собственные значения матрицы вторых производных, на основании которых мы можем судить, является ли найденная нами критическая точка минимумом, переходным состоянием или критической точкой более высокого порядка. Напомним, что если матрица положительно определена, то критическая точка является минимумом. 72

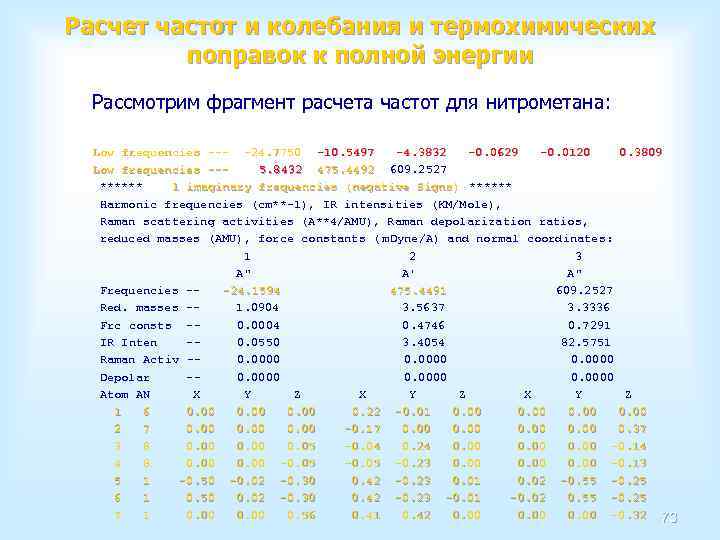Расчет частот и колебания и термохимических поправок к полной энергии Рассмотрим фрагмент расчета частот для нитрометана: Low frequencies --- -24. 7750 -10. 5497 -4. 3832 -0. 0629 -0. 0120 0. 3809 Low frequencies --5. 8432 475. 4492 609. 2527 ****** 1 imaginary frequencies (negative Signs) ****** Harmonic frequencies (cm**-1), IR intensities (KM/Mole), Raman scattering activities (A**4/AMU), Raman depolarization ratios, reduced masses (AMU), force constants ( m. Dyne/A) and normal coordinates: 1 2 3 A" A' A" Frequencies --24. 1594 475. 4491 609. 2527 Red. masses -1. 0904 3. 5637 3. 3336 Frc consts -0. 0004 0. 4746 0. 7291 IR Inten -0. 0550 3. 4054 82. 5751 Raman Activ -0. 0000 Depolar -0. 0000 Atom AN X Y Z 1 6 0. 00 0. 22 -0. 01 0. 00 2 7 0. 00 -0. 17 0. 00 0. 37 3 8 0. 00 0. 05 -0. 04 0. 24 0. 00 -0. 14 4 8 0. 00 -0. 05 -0. 23 0. 00 -0. 13 5 1 -0. 50 -0. 02 -0. 30 0. 42 -0. 23 0. 01 0. 02 -0. 55 -0. 25 6 1 0. 50 0. 02 -0. 30 0. 42 -0. 23 -0. 01 -0. 02 0. 55 -0. 25 7 1 0. 00 0. 56 0. 41 0. 42 0. 00 -0. 32 73

Поправки на нулевые колебания Энергия в колебательных движениях молекул квантована. Ее величина для так называемого гармонического осциллятора может быть найдена из выражения (Рис. 16): где V − колебательное квантовое число, принимающее значения натуральных чисел: 0, 1, 2, . . . ; ν − частота основного колебания в см-1, определяемая уравнением: где с − скорость света; k − силовая постоянная связи; m − приведенная масса системы, вычисляемая через массы атомов по формуле: Силовая постоянная k увеличивается с возрастанием прочности связи между атомами. 74

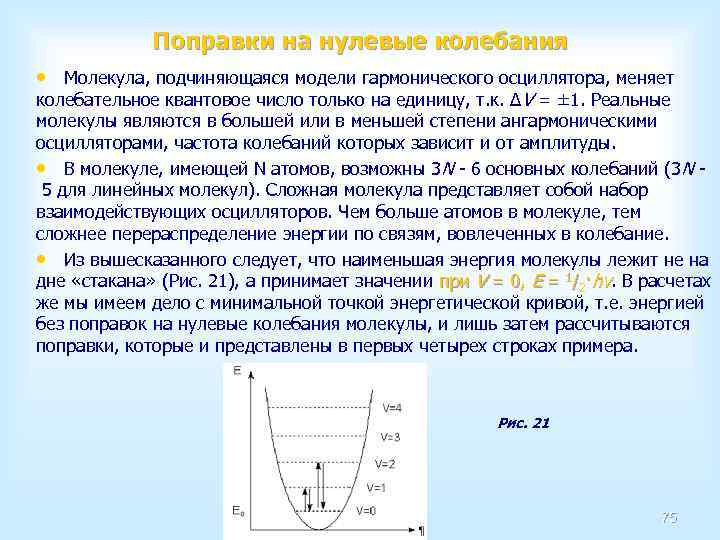Поправки на нулевые колебания • Молекула, подчиняющаяся модели гармонического осциллятора, меняет колебательное квантовое число только на единицу, т. к. Δ V = ± 1. Реальные молекулы являются в большей или в меньшей степени ангармоническими осцилляторами, частота колебаний которых зависит и от амплитуды. • В молекуле, имеющей N атомов, возможны 3 N - 6 основных колебаний (3 N 5 для линейных молекул). Сложная молекула представляет собой набор взаимодействующих осцилляторов. Чем больше атомов в молекуле, тем сложнее перераспределение энергии по связям, вовлеченных в колебание. • Из вышесказанного следует, что наименьшая энергия молекулы лежит не на дне «стакана» (Рис. 21), а принимает значении при V = 0, Е = 1/2·hν. В расчетах же мы имеем дело с минимальной точкой энергетической кривой, т. е. энергией без поправок на нулевые колебания молекулы, и лишь затем рассчитываются поправки, которые и представлены в первых четырех строках примера. Рис. 21 75

Расчет частот колебания и термохимических поправок к полной энергии Расчет термохимических поправок к полной энергии молекулы и суммарных абсолютных энергий завершается выводом на экран следующей информации: Zero-point correction= Thermal correction to Energy= Thermal correction to Enthalpy= Thermal correction to Gibbs Free Energy= Sum of electronic and zero-point Energies= Sum of electronic and thermal Enthalpies= Sum of electronic and thermal Free Energies= 0. 049148 (Hartree/Particle) 0. 052671 0. 053615 0. 023319 0. 023644 0. 027166 0. 028110 -0. 002185 76

Анализ точности полученного решения при расчете Freq Процедура оптимизации является итерационной и расчет матрицы Гессе ведется приближенно по некоторым рекуррентным формулам. В результате этого в ходе расчета может накапливаться ошибка, которая возможно приведет к досрочному достижению критериев сходимости и, как следствие, к завершению процесса оптимизации. Процедура расчета частот колебаний и поправок к полным энергиям молекулы вычисляет значения критериев сходимости для конечных геометрических параметров и оценивает их величину относительно их допустимых значений. Например, для нитрометана: Item Value Threshold Converged? Maximum Force 0. 000092 0. 000450 YES RMS Force 0. 000028 0. 000300 YES Maximum Displacement 0. 000190 0. 001800 YES RMS Displacement 0. 000080 0. 001200 YES Predicted change in Energy=-1. 366499 D-08 Optimization completed. 77

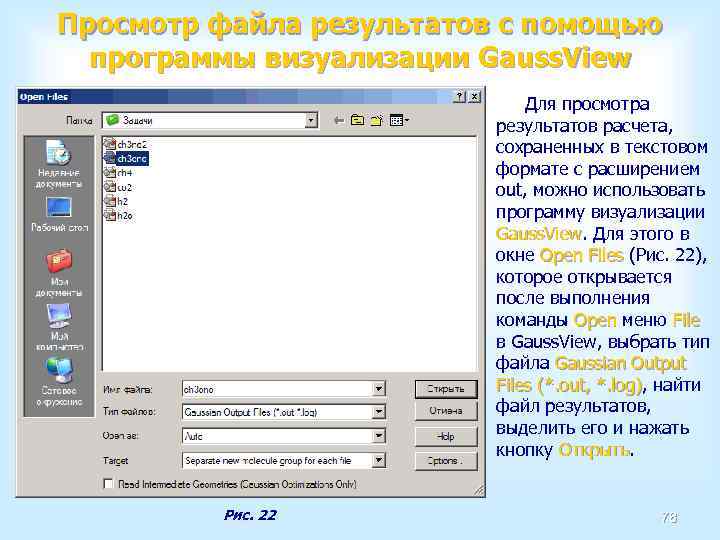Просмотр файла результатов с помощью программы визуализации Gauss. View Для просмотра результатов расчета, сохраненных в текстовом формате с расширением out, можно использовать программу визуализации Gauss. View. Для этого в Gauss. View окне Open Files (Рис. 22), Open Files которое открывается после выполнения команды Open меню File Open File в Gauss. View, выбрать тип файла Gaussian Output Files (*. out, *. log), найти Files (*. out, *. log) файл результатов, выделить его и нажать кнопку Открыть Рис. 22 78

Просмотр файла результатов с помощью программы визуализации Gauss. View После этого в поле построения молекул появится рассчитанная (например, оптимизированная) структура химического соединения. Для него легко можно промерить все длины связи (в Å), валентные и двугранные углы (в градусах), если выделить курсором мыши соответствующие атомы. При этом значения геометрических параметров показываются в нижней части окна (Рис. 23). Рис. 23 79

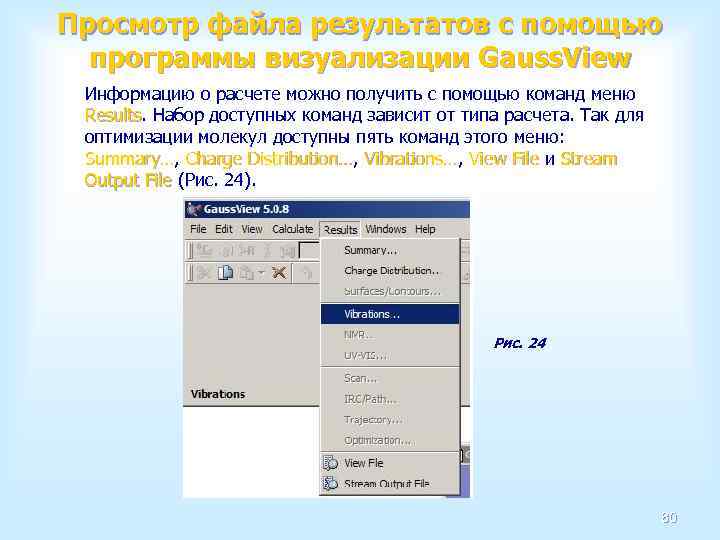Просмотр файла результатов с помощью программы визуализации Gauss. View Информацию о расчете можно получить с помощью команд меню Results. Набор доступных команд зависит от типа расчета. Так для Results оптимизации молекул доступны пять команд этого меню: Summary…, Charge Distribution…, Vibrations…, View File и Stream Summary… Charge Distribution… Vibrations… View File Output File (Рис. 24). Output File Рис. 24 80

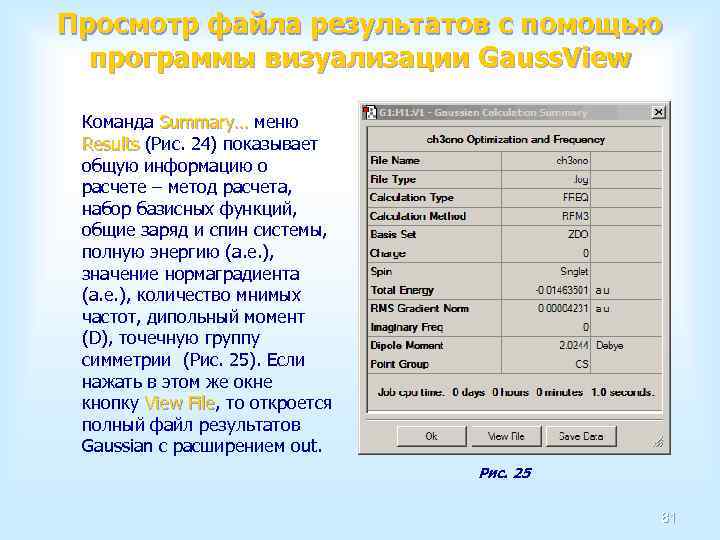Просмотр файла результатов с помощью программы визуализации Gauss. View Команда Summary… меню Summary… Results (Рис. 24) показывает общую информацию о расчете – метод расчета, набор базисных функций, общие заряд и спин системы, полную энергию (а. е. ), значение нормаградиента (а. е. ), количество мнимых частот, дипольный момент (D), точечную группу симметрии (Рис. 25). Если нажать в этом же окне кнопку View File, то откроется View File полный файл результатов Gaussian с расширением out. Рис. 25 81

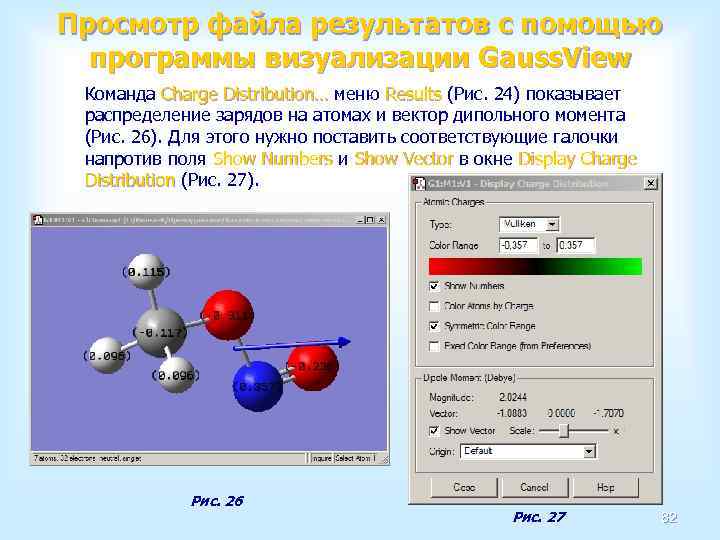Просмотр файла результатов с помощью программы визуализации Gauss. View Команда Charge Distribution… меню Results (Рис. 24) показывает Charge Distribution… распределение зарядов на атомах и вектор дипольного момента (Рис. 26). Для этого нужно поставить соответствующие галочки напротив поля Show Numbers и Show Vector в окне Display Charge Show Numbers Show Vector Distribution (Рис. 27). Distribution Рис. 26 Рис. 27 82

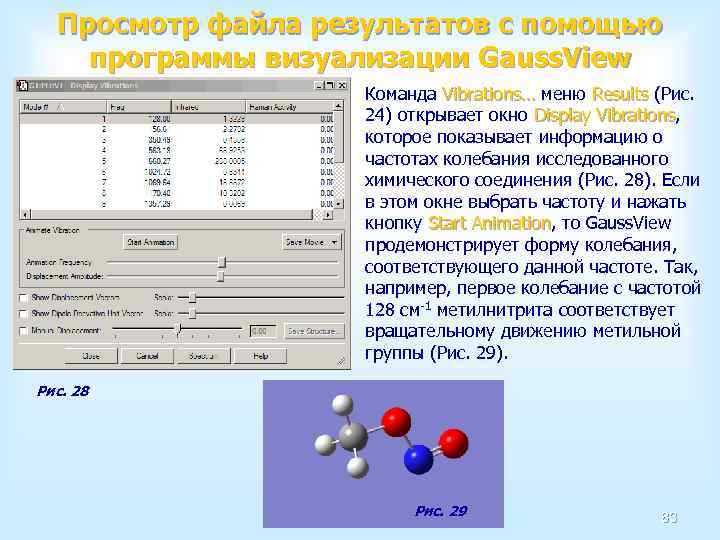Просмотр файла результатов с помощью программы визуализации Gauss. View Команда Vibrations… меню Results (Рис. Vibrations… 24) открывает окно Display Vibrations, Display Vibrations которое показывает информацию о частотах колебания исследованного химического соединения (Рис. 28). Если в этом окне выбрать частоту и нажать кнопку Start Animation, то Gauss. View Start Animation продемонстрирует форму колебания, соответствующего данной частоте. Так, например, первое колебание с частотой 128 см-1 метилнитрита соответствует вращательному движению метильной группы (Рис. 29). Рис. 28 Рис. 29 83

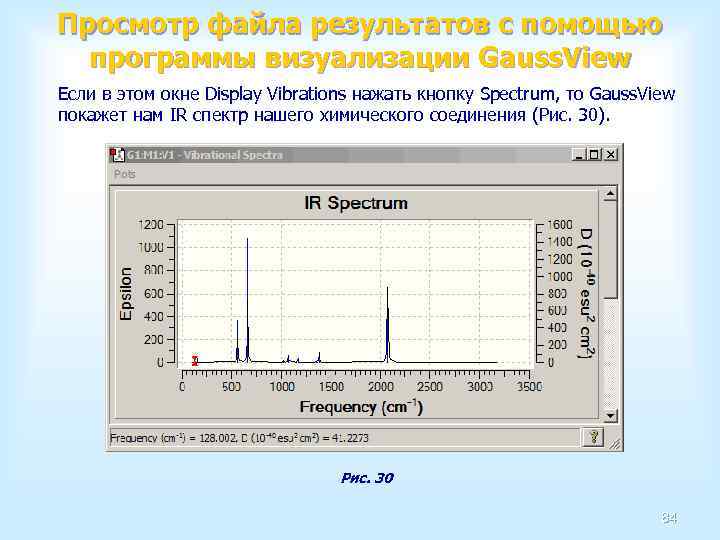Просмотр файла результатов с помощью программы визуализации Gauss. View Если в этом окне Display Vibrations нажать кнопку Spectrum, то Gauss. View покажет нам IR спектр нашего химического соединения (Рис. 30). Рис. 30 84

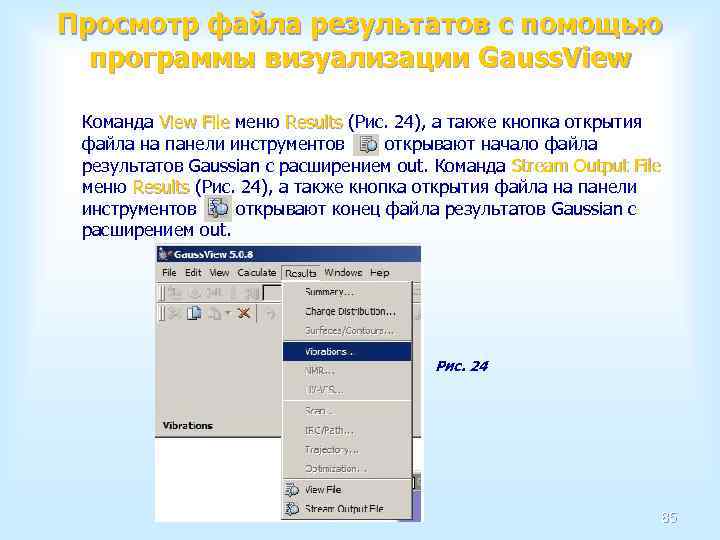Просмотр файла результатов с помощью программы визуализации Gauss. View Команда View File меню Results (Рис. 24), а также кнопка открытия View File файла на панели инструментов открывают начало файла результатов Gaussian с расширением out. Команда Stream Output File меню Results (Рис. 24), а также кнопка открытия файла на панели инструментов открывают конец файла результатов Gaussian с расширением out. Рис. 24 85

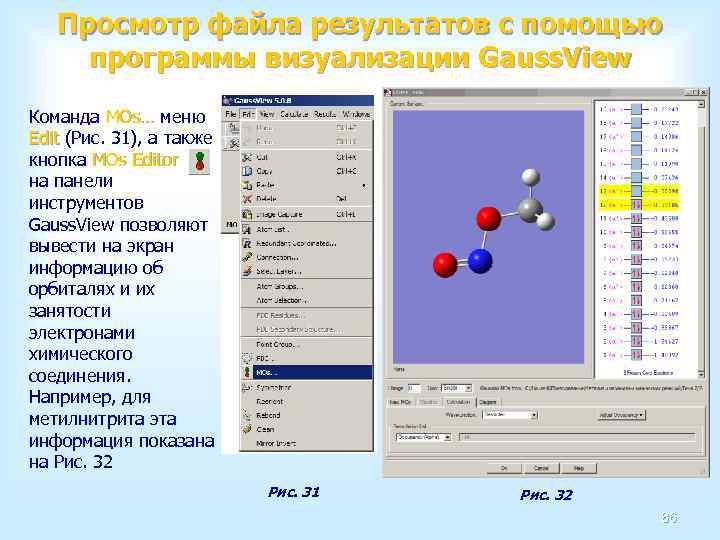Просмотр файла результатов с помощью программы визуализации Gauss. View Команда MOs… меню Edit (Рис. 31), а также кнопка MOs Editor на панели инструментов Gauss. View позволяют вывести на экран информацию об орбиталях и их занятости электронами химического соединения. Например, для метилнитрита эта информация показана на Рис. 32 Рис. 31 Рис. 32 86

Ошибки в ходе оптимизации • задания начальной геометрии – синтаксические (неправильное задания начальной геометрии написание символов элементов) и логические (несоответствие типов данных, например, расстоянии между атомами менее 0. 3 Å); • работы процедуры самосогласования (процедуры SCF) – работы процедуры самосогласования несходимость, некорректно формирующееся стартовое приближение или некорректное приближение, получено в процессе оптимизации. Обойти создавшуюся ситуацию в случае несходимости можно, изменив алгоритм SCF, увеличить количество итераций SCF, ухудшить критерии сходимости (по понятным причинам, последними двумя способами нужно пользоваться с большой осторожностью). В случае проблем с приближением можно исправить стартовую геометрию, попытаться сформулировать корректное стартовое приближение и далее использовать его (Guess=Read), проанализировать результат (в случае, когда некорректное приближение возникло в результате оптимизации) и попробовать продолжить расчет с полученной геометрией, но пересчитав начальное приближение; 87

Ошибки в ходе оптимизации • • 1. 2. 3. в геометрии, полученные в результате оптимизации – выход в геометрии валентного угла за пределы 0 -180 о, изменение точечной группы симметрии; не достигнуто минимальное значение энергии за заданное количество итераций. Это может возникнуть из-за: количество итераций неудачно заданной начальной геометрии, вследствие чего исследование движется в неправильном направлении или вообще расходится; выхода на плато энергии и очень медленного движения по нему в минимум; зацикливания – расчет двигается между несколькими эквивалентными состояниями. Исправить эти ошибки можно, внеся изменения в исходную геометрию или продолжив из конечной точки с увеличением количества шагов или выбрав другой алгоритм поиска минимума, начав расчет из точки с минимальной энергией. 88

Расчет энтальпии образования, энергии Гиббса, энтропии соединений, энтальпии реакции Как мы уже говорили в Gaussain мы получаем абсолютные энергии при 0 К и 298. 15 К, абсолютные энтальпии и свободные энергии Гиббса при 298. 15 К систем в Hartree, например для нитрометана: Sum Sum of of electronic and and zero-point Energies= thermal Enthalpies= thermal Free Energies= 0. 023644 0. 027166 0. 028110 -0. 002185 На основании этих данных можно рассчитать энергетические характеристики исследуемых соединения или переходных состояний реакций. 89

Расчет энтальпии образования соединений выполняется по формуле где − энтальпия образования исследуемого соединения; − абсолютная энтальпия образования исследуемого соединения, получаемая в GAUSSIAN (в атомных единицах HARTREE); − абсолютная энтальпия образования i-го атома, входящего в исследуемое соединение, получаемая в GAUSSIAN (HARTREE); − справочные данные по энтальпии образования i-го атома, входящего в исследуемое соединение (к. Дж/моль); − количество i-х атомов, входящих в исследуемое соединение; − коэффициенты перевода HARTREE в к. Дж/моль. 90

Расчет энергии Гиббса соединений выполняется по формуле где − энергия Гиббса исследуемого соединения; − абсолютная энергия Гиббса исследуемого соединения, получаемая в GAUSSIAN (в атомных единицах HARTREE); − абсолютная энергия Гиббса i-го атома, входящего в исследуемое соединение, получаемая в GAUSSIAN (HARTREE); − справочные данные по энергиям Гиббса i-го атома, входящего в исследуемое соединение (к. Дж/моль); − количество i-х атомов, входящих в исследуемое соединение; − коэффициенты перевода HARTREE в к. Дж/моль. 91

Расчет энтропии соединений выполняется по формуле где − энтропия исследуемого соединения (Дж/моль К); − энергия Гиббса исследуемого соединения (к. Дж/моль) ; − справочные данные по энергии Гиббса i-го атома, входящего в исследуемое соединение (к. Дж/моль); − энтальпия образования исследуемого соединения (к. Дж/моль); − справочные данные по энтальпии образования i-го атома, входящего в исследуемое соединение (к. Дж/моль); − справочные данные по энтропии i-го атома, входящего в исследуемое соединение (Дж/моль*К) − количество i-х атомов, входящих в исследуемое соединение 92

Расчет абсолютных термодинамических характеристик атомов с помощью пакета прикладных программ Gaussian Формулы расчета термодинамических характеристик химических соединений включают в себя абсолютные термодинамические характеристики (HARTREE) атомов, из которых состоит данное исследуемое химическое соединение, атомов полученные в рамках того же самого квантово-химического метода, что и для в рамках того же самого квантово-химического метода химического соединения. Рассчитываются они аналогичным способом, что и для самого химического соединения. Ниже приведены примеры исходных файлов Gaussian для оптимизации атомов водорода, углерода, азота и кислорода и расчета их абсолютных значений термодинамических характеристик: %mem=200 Mb %chk=H_PM 3. chk # PM 3 Opt=(Max. Cycle=100) Freq SCF=(Max. Cycle=500) Atom of hydrogen 0 2 H 93

Расчет абсолютных термодинамических характеристик атомов с помощью пакета прикладных программ Gaussian %mem=200 Mb %chk=C_PM 3. chk # PM 3 Opt=(Max. Cycle=100) Freq SCF=(Max. Cycle=500) Atom of carbon 0 3 C %mem=300 Mb %chk=N_PM 3. chk #T freq opt=(VTight) PM 3 scf=(QC, Pass, In. Core) Trans=In. Core N(s 2 p 3) 0 4 N %mem=300 Mb %chk=O_PM 3. chk #T freq opt=(VTight) PM 3 scf=(QC, Pass, In. Core) Trans=In. Core O(s 2 p 4) 0 3 O 94

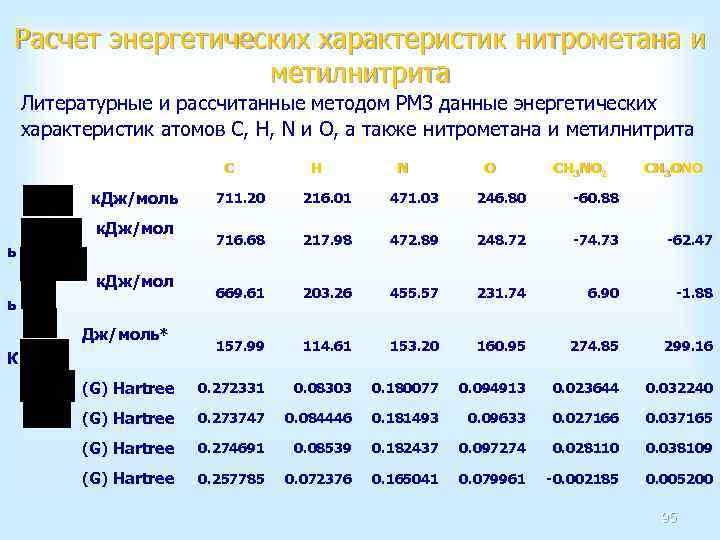Расчет энергетических характеристик нитрометана и метилнитрита Литературные и рассчитанные методом PM 3 данные энергетических характеристик атомов C, H, N и O, а также нитрометана и метилнитрита C к. Дж/моль H N O CH 3 NO 2 CH 3 ONO 711. 20 216. 01 471. 03 246. 80 -60. 88 716. 68 217. 98 472. 89 248. 72 -74. 73 -62. 47 669. 61 203. 26 455. 57 231. 74 6. 90 -1. 88 157. 99 114. 61 153. 20 160. 95 274. 85 299. 16 (G) Hartree 0. 272331 0. 08303 0. 180077 0. 094913 0. 023644 0. 032240 (G) Hartree 0. 273747 0. 084446 0. 181493 0. 09633 0. 027166 0. 037165 (G) Hartree 0. 274691 0. 08539 0. 182437 0. 097274 0. 028110 0. 038109 (G) Hartree 0. 257785 0. 072376 0. 165041 0. 079961 -0. 002185 0. 005200 к. Дж/мол ь Дж/моль* К 95

Расчет энальпии реакции Расчет энтальпии реакции соединений выполняется по одной из формул: где энтальпия реакции; энтальпия образования реагентов; энтальпия образования продуктов реакции; абсолютная энтальпия образования реагентов реакции; абсолютная энтальпия образования продуктов реакции; − коэффициенты перевода HARTREE в к. Дж/моль. 96

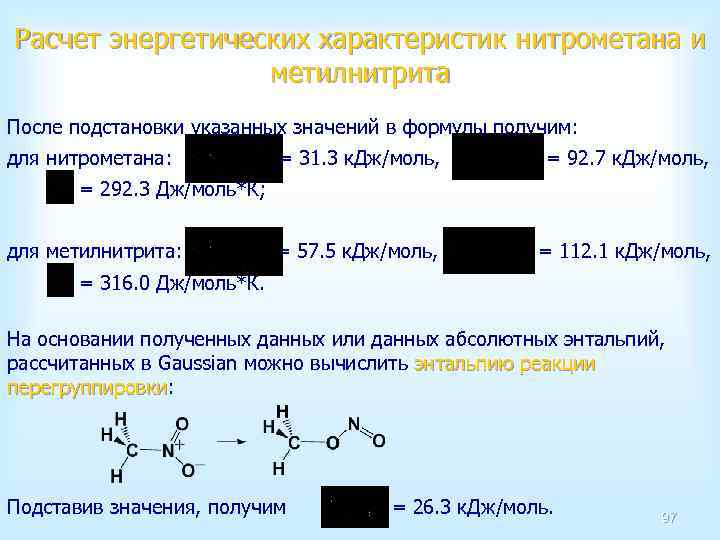Расчет энергетических характеристик нитрометана и метилнитрита После подстановки указанных значений в формулы получим: для нитрометана: = 31. 3 к. Дж/моль, = 92. 7 к. Дж/моль, = 292. 3 Дж/моль*К; для метилнитрита: = 57. 5 к. Дж/моль, = 112. 1 к. Дж/моль, = 316. 0 Дж/моль*К. На основании полученных данных или данных абсолютных энтальпий, рассчитанных в Gaussian можно вычислить энтальпию реакции перегруппировки: перегруппировки Подставив значения, получим = 26. 3 к. Дж/моль. 97