Перпендикулярность в пространстве Определения и признаки l Перпендикуляр

Перпендикулярность в пространстве Определения и признаки l Перпендикуляр и наклонная, теорема о трех перпендикулярах l Ортогональное проектирование l Двугранный угол l Измерение расстояний и углов в пространстве l

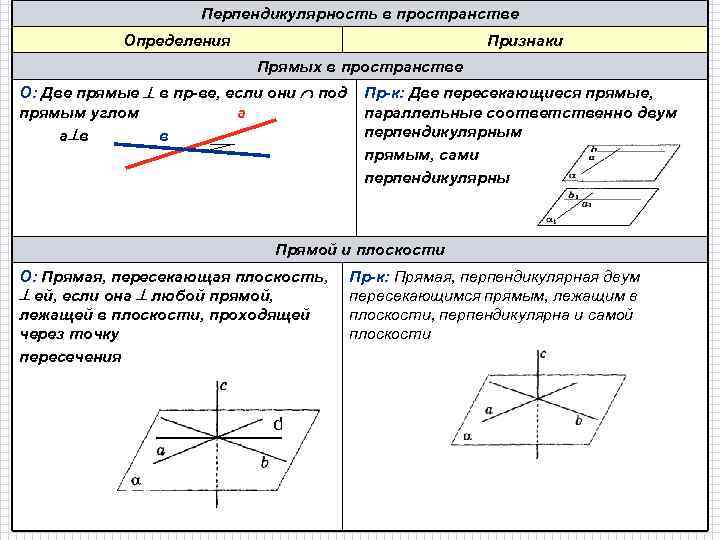Перпендикулярность в пространстве Определения Признаки Прямых в пространстве О: Две прямые в пр-ве, если они под прямым углом а а в в Пр-к: Две пересекающиеся прямые, параллельные соответственно двум перпендикулярным прямым, сами перпендикулярны Прямой и плоскости О: Прямая, пересекающая плоскость, ей, если она любой прямой, лежащей в плоскости, проходящей через точку пересечения d Пр-к: Прямая, перпендикулярная двум пересекающимся прямым, лежащим в плоскости, перпендикулярна и самой плоскости

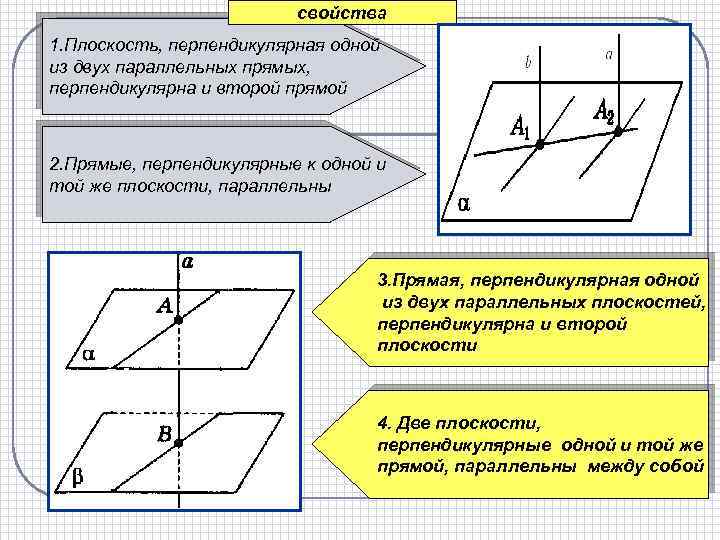свойства 1. Плоскость, перпендикулярная одной из двух параллельных прямых, перпендикулярна и второй прямой 2. Прямые, перпендикулярные к одной и той же плоскости, параллельны 3. Прямая, перпендикулярная одной из двух параллельных плоскостей, перпендикулярна и второй плоскости 4. Две плоскости, перпендикулярные одной и той же прямой, параллельны между собой

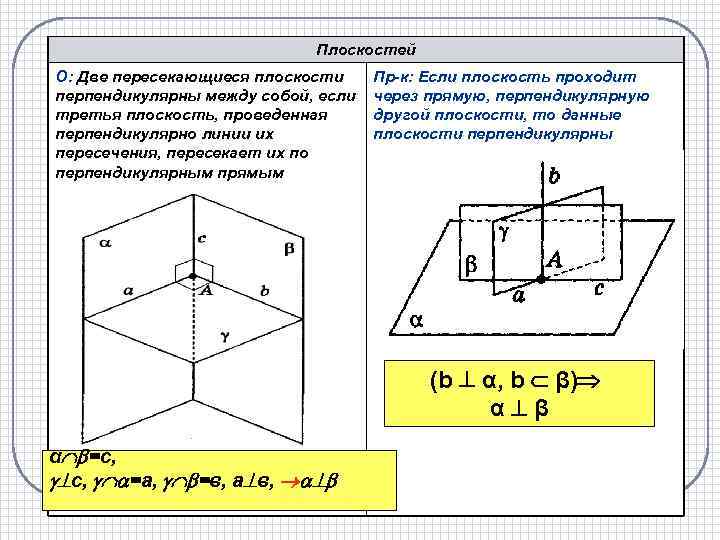Плоскостей О: Две пересекающиеся плоскости перпендикулярны между собой, если третья плоскость, проведенная перпендикулярно линии их пересечения, пересекает их по перпендикулярным прямым Пр-к: Если плоскость проходит через прямую, перпендикулярную другой плоскости, то данные плоскости перпендикулярны (b α, b β) α β α =с, с, =а, =в, а в,

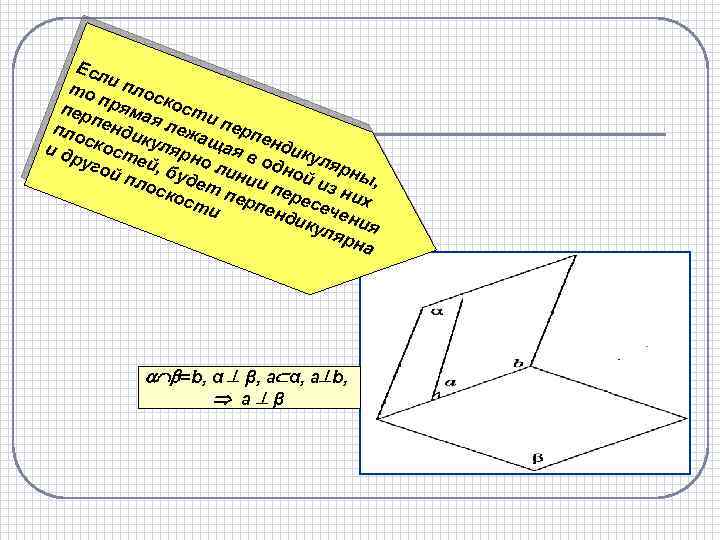Есл то и пло с пер пряма кост и пло пенди я леж перп а е к и д скост уляр щая в ндику н руг ой ей, бу о лин одной лярны пло д и ско ет пе и пер из ни , х ст рпе есе и нди чен кул ия ярн а =b, α β, а α, a b, а β

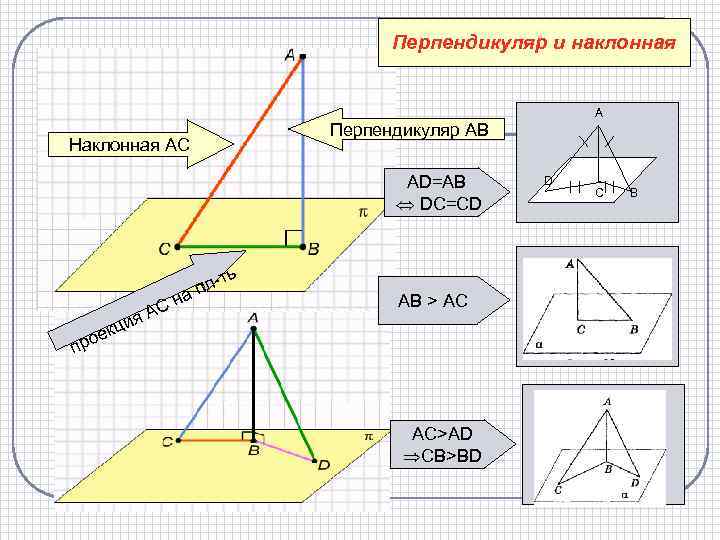Перпендикуляр и наклонная Наклонная АС Перпендикуляр АВ AD=AB DC=CD С я. А н ть пла А АВ > AC и екц ро п AC>AD CB>BD D C B

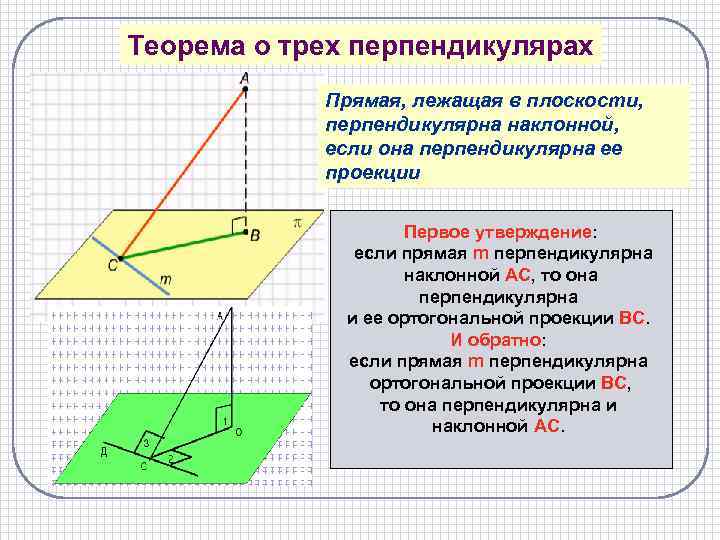Теорема о трех перпендикулярах Прямая, лежащая в плоскости, перпендикулярна наклонной, если она перпендикулярна ее проекции Первое утверждение: если прямая m перпендикулярна наклонной АС, то она перпендикулярна и ее ортогональной проекции ВС. И обратно: если прямая m перпендикулярна ортогональной проекции ВС, то она перпендикулярна и наклонной АС.

Ортогональная проекция

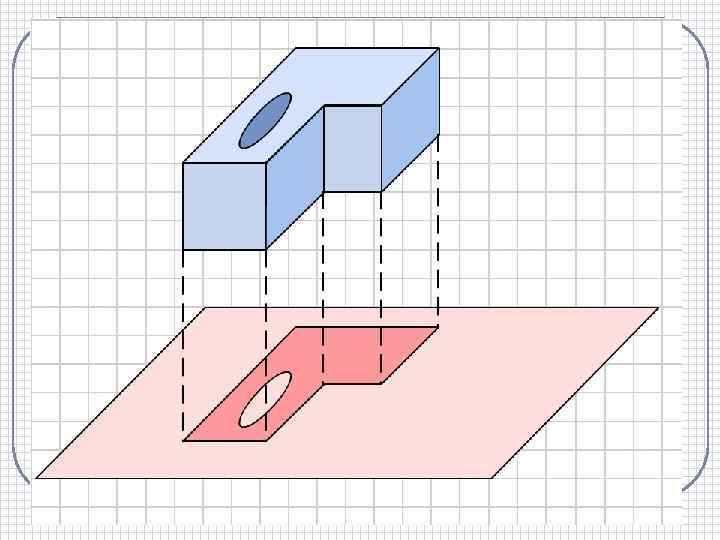
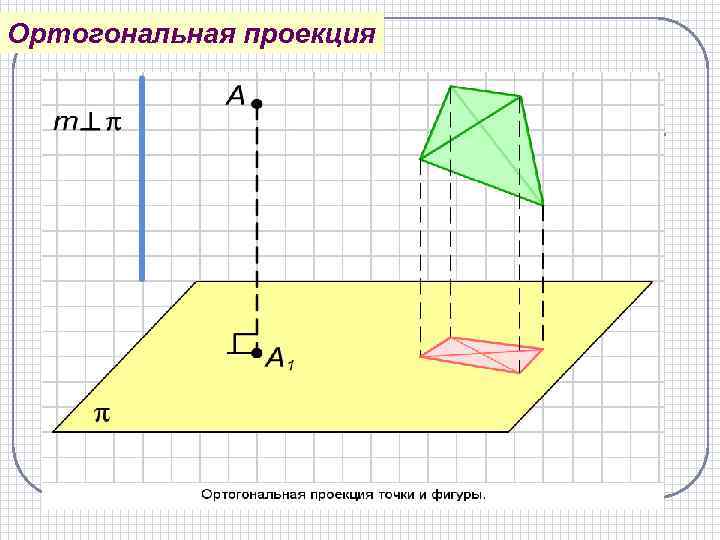
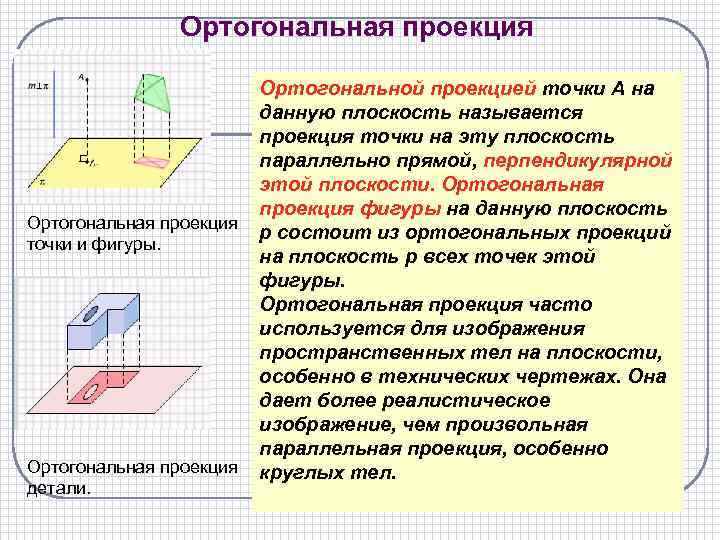Ортогональная проекция точки и фигуры. Ортогональная проекция детали. Ортогональной проекцией точки А на данную плоскость называется проекция точки на эту плоскость параллельно прямой, перпендикулярной этой плоскости. Ортогональная проекция фигуры на данную плоскость p состоит из ортогональных проекций на плоскость p всех точек этой фигуры. Ортогональная проекция часто используется для изображения пространственных тел на плоскости, особенно в технических чертежах. Она дает более реалистическое изображение, чем произвольная параллельная проекция, особенно круглых тел.

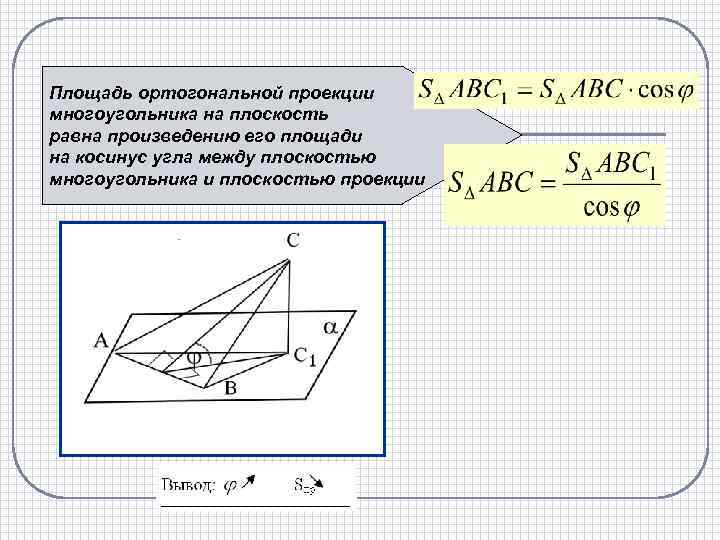Площадь ортогональной проекции многоугольника на плоскость равна произведению его площади на косинус угла между плоскостью многоугольника и плоскостью проекции

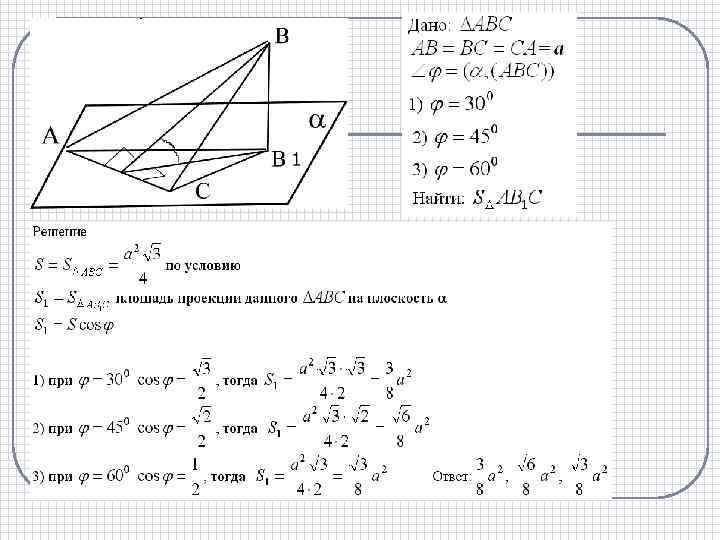
Измерение расстояний в пространстве

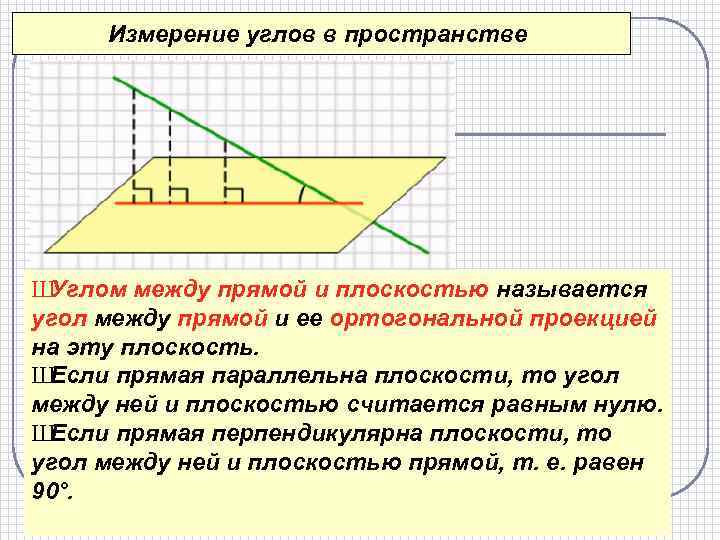Измерение углов в пространстве Ш Углом между прямой и плоскостью называется угол между прямой и ее ортогональной проекцией на эту плоскость. Ш Если прямая параллельна плоскости, то угол между ней и плоскостью считается равным нулю. Ш Если прямая перпендикулярна плоскости, то угол между ней и плоскостью прямой, т. е. равен 90°.

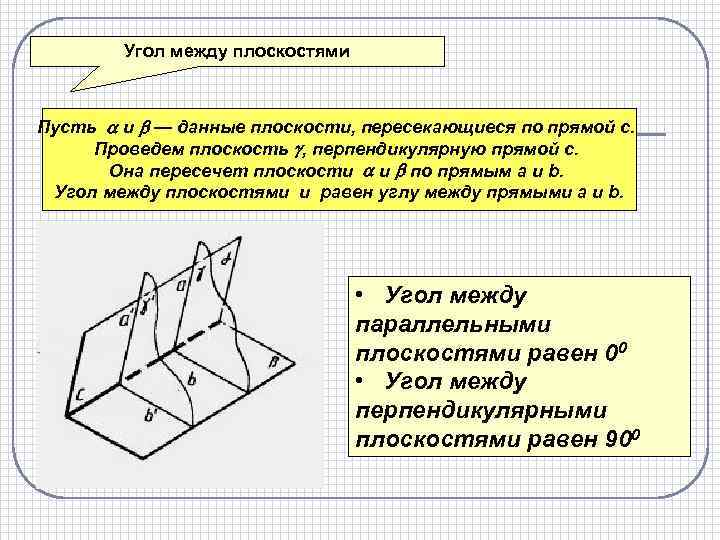Угол между плоскостями Пусть и — данные плоскости, пересекающиеся по прямой с. Проведем плоскость , перпендикулярную прямой с. Она пересечет плоскости и по прямым а и b. Угол между плоскостями и равен углу между прямыми а и b. • Угол между параллельными плоскостями равен 00 • Угол между перпендикулярными плоскостями равен 900

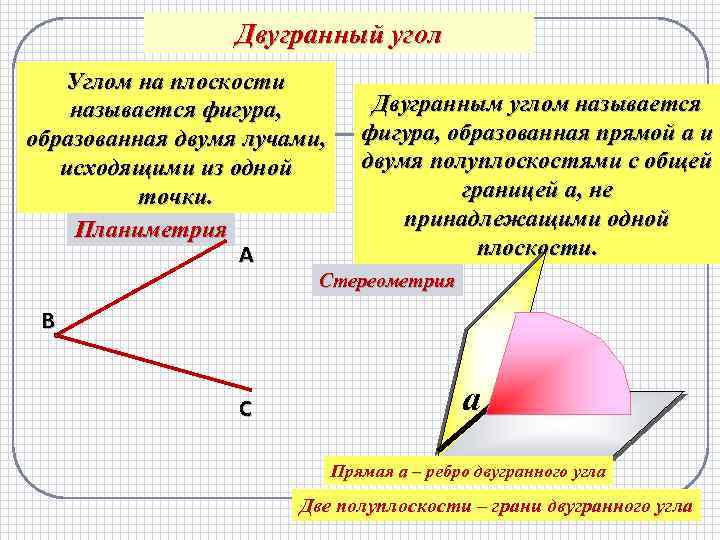Двугранный угол Углом на плоскости называется фигура, образованная двумя лучами, исходящими из одной точки. Планиметрия А Двугранным углом называется фигура, образованная прямой a и двумя полуплоскостями с общей границей a, не принадлежащими одной плоскости. Стереометрия В С а Прямая a – ребро двугранного угла Две полуплоскости – грани двугранного угла

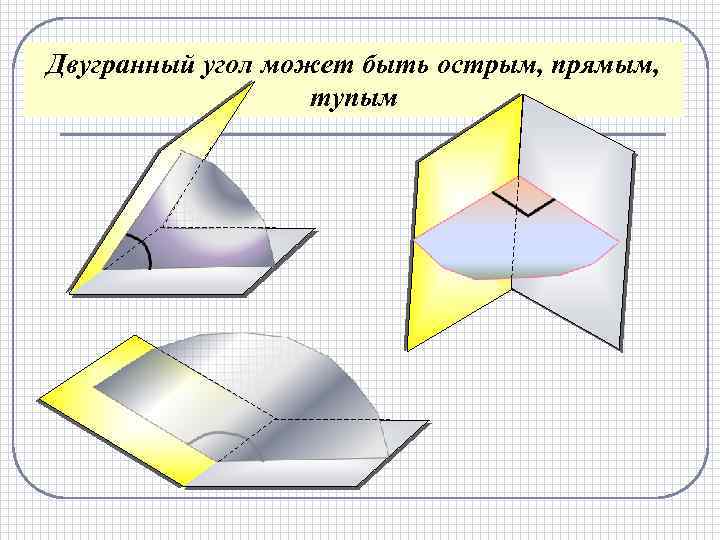Двугранный угол может быть острым, прямым, тупым

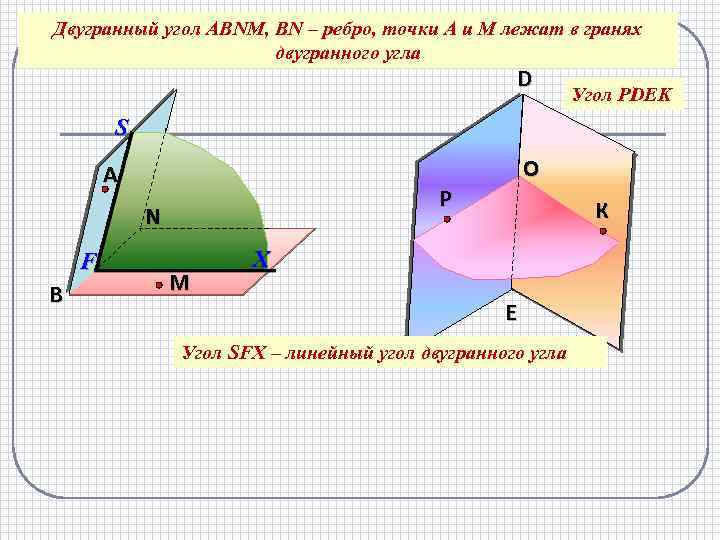Двугранный угол АВNМ, ВN – ребро, точки А и М лежат в гранях двугранного угла D Угол РDEK S А Р N F В O M К X E Угол SFX – линейный угол двугранного угла

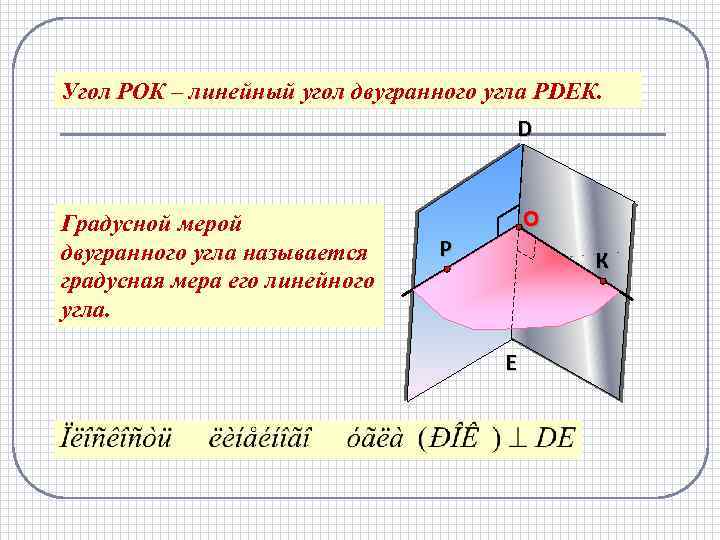Угол РОК – линейный угол двугранного угла РDEК. D Градусной мерой двугранного угла называется градусная мера его линейного угла. O Р К E

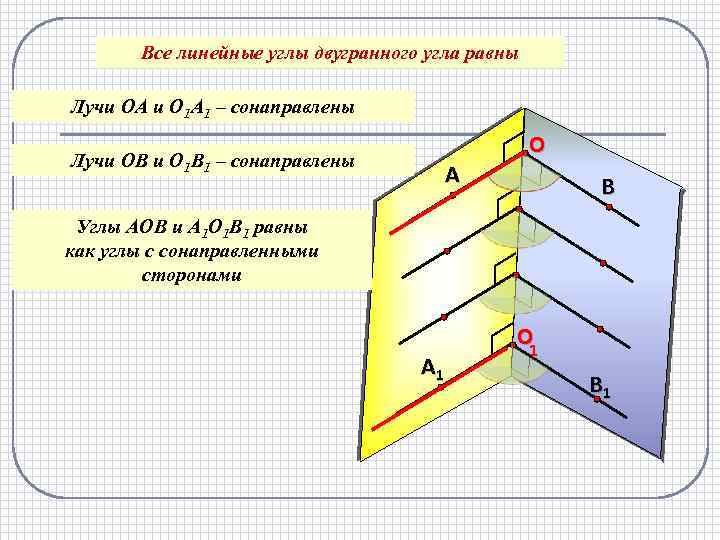Все линейные углы двугранного угла равны Лучи ОА и О 1 А 1 – сонаправлены Лучи ОВ и О 1 В 1 – сонаправлены А O В Углы АОВ и А 1 О 1 В 1 равны как углы с сонаправленными сторонами А 1 O 1 В 1