Перпендикулярность прямой и плоскости Подготовила студентка 1 курса

Перпендикулярность прямой и плоскости Подготовила студентка 1 курса 13 группы Халилова Севинч

• Определение Прямая, пересекающая плоскость, называется перпендикулярной этой плоскости, если она перпендикулярна каждой прямой, которая лежит в данной плоскости и проходит через точку пересечения.

• Теорема 1 ПРИЗНАК ПЕРПЕНДИКУЛЯРНОСТИ ПРЯМОЙ И ПЛОСКОСТИ. Если прямая, пересекающая плоскость, перпендикулярна двум прямым в этой плоскости, проходящим через точку пересечения данной прямой и плоскости, то она перпендикулярна плоскости.

• Доказательство: Докажем, что прямая а перпендикулярна плоскости. Отложим на прямой а от точки А в разные стороны равные отрезки АА 1 и. АА 2. Треугольники А 1 СА 2 и А 1 ВА 2 равнобедренный, т. к. отрезок АС является высотой (АА 1=АА 2). Следовательно, треугольники А 1 ВС и А 2 ВС равны по трем сторонам. Из равенства треугольников А 1 ВС и А 2 ВС следует равенство углов и треугольников А 1 ВХ и. А 2 ВХ по двум сторонам и углу между ними. Из равенства сторон А 1 Х и А 2 Х этих треугольников заключаем, что треугольник А 1 ХА 2 равнобедренный. Поэтому его медиана ХА является также высотой. А это и значит, что прямая х перпендикулярна а. По определению прямая а перпендикулярна плоскости. Теорема доказана.

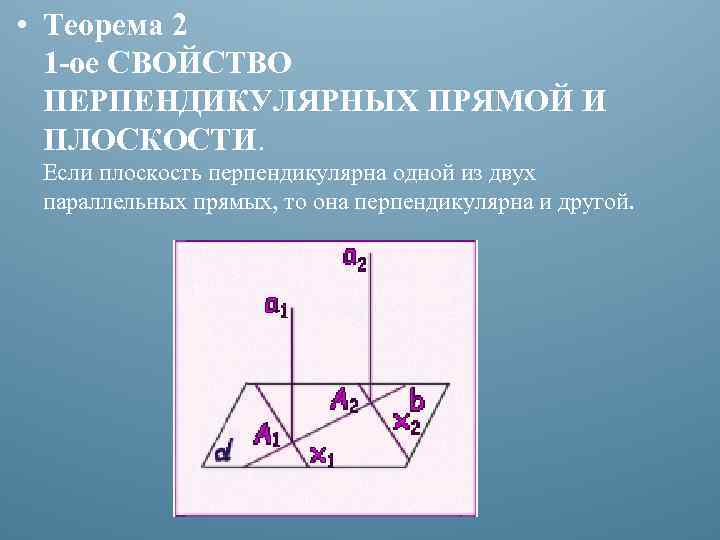• Теорема 2 1 -ое СВОЙСТВО ПЕРПЕНДИКУЛЯРНЫХ ПРЯМОЙ И ПЛОСКОСТИ. Если плоскость перпендикулярна одной из двух параллельных прямых, то она перпендикулярна и другой.

• Доказательство: Пусть а 1 и а 2 - 2 параллельные прямые и плоскость, перпендикулярная прямой а 1. Докажем, что эта плоскость перпендикулярна и прямой а 2. Проведем через точку А 2 пересечения прямой а 2 с плоскостью произвольную прямую х2 в плоскости. Проведем в плоскости через точку А 1 пересечения прямой а 1 с прямую х1, параллельную прямой х2. Так как прямая а 1 перпендикулярна плоскости , то прямые а 1 и x 1 перпендикулярны. А по теореме 1 параллельные им пересекающиеся прямые а 2 и х2 тоже перпендикулярны. Таким образом, прямая а 2 перпендикулярна любой прямой х2 в плоскости. А это ( по определению )значит, что прямая а 2 перпендикулярна плоскости. Теорема доказана.

• Теорема 3 2 -ое СВОЙСТВО ПЕРПЕНДИКУЛЯРНЫХ ПРЯМОЙ И ПЛОСКОСТИ. Две прямые, перпендикулярные одной и той же плоскости, параллельны.

• Доказательство: Пусть а и b - 2 прямые, перпендикулярные плоскости. Допутим, что прямые а и b не параллельны. Выберем на прямой b точку С, не лежащую в плоскости. Проведем через точку С прямую b 1, параллельную прямой а. Прямая b 1 перпендикулярна плоскости по теореме 2. Пусть В и В 1 - точки пересечения прямых b иb 1 с плоскостью. Тогда прямая ВВ 1 перпендикулярна пересекающимся прямым b и b 1. А это невозможно. Мы пришли к противоречию. Теорема доказана.

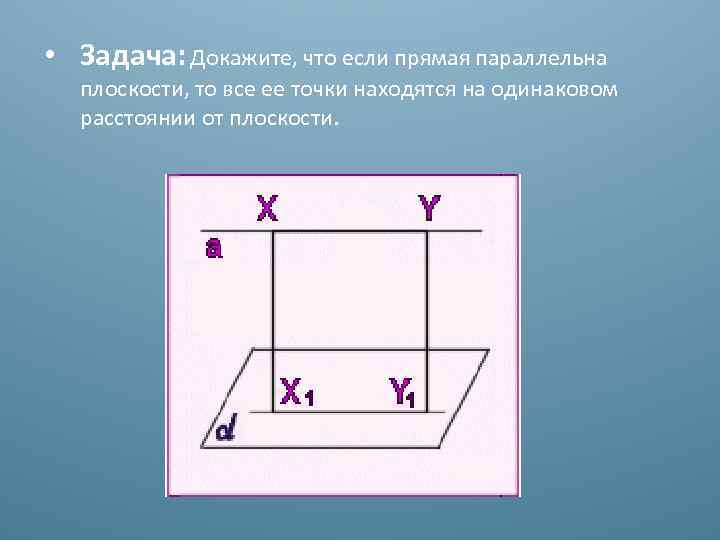• Задача: Докажите, что если прямая параллельна плоскости, то все ее точки находятся на одинаковом расстоянии от плоскости.

• Решение: Пусть а - данная прямая и - данная плоскость. Возьмем на прямой а две произвольные точки Х и Y. По теореме 3 прямые ХХ 1 и YY 1 параллельны, следовательно, лежат в одной плоскости. Эта плоскость пересекает плоскость по прямой Х 1 Y 1, прямая а параллельна прямой Х 1 Y 1, так как не пересекает содержащую её плоскость. Итак у четырехугольника ХХ 1 YY 1 противолежащие стороны параллельны. Следовательно, он параллелограмм, а значит ХХ 1=YY 1.