Перпендикулярность прямой и плоскости Опр Две прямые в

Перпендикулярность прямой и плоскости Опр. Две прямые в пространстве называются перпендикулярными, если угол между ними равен 90º. Лемма Если одна из 2 -х параллельных прямых, перпендикулярна третьей прямой, то и другая прямая перпендикулярна к этой прямой. а b М с С Доказательство А

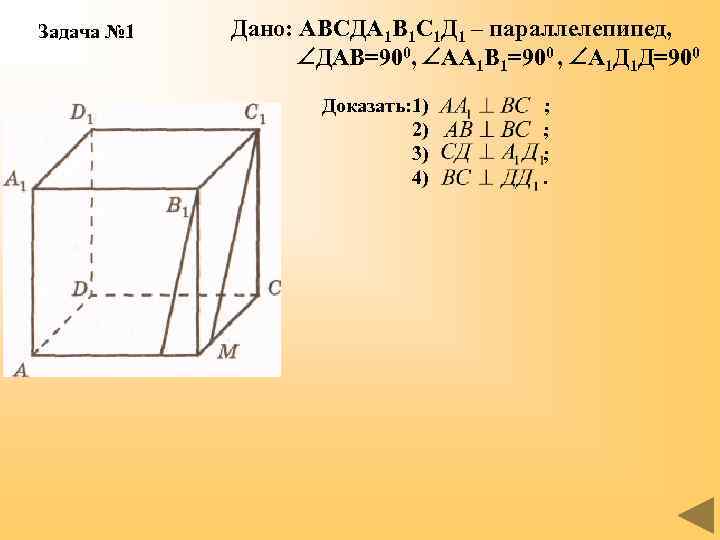Задача № 1 Дано: АВСДА 1 В 1 С 1 Д 1 – параллелепипед, ДАВ=900, АА 1 В 1=900 , А 1 Д 1 Д=900 Доказать: 1) 2) 3) 4) ; ; ; .

Прямая перпендикулярная плоскости Опр. Прямая называется перпендикулярной плоскости, если она перпендикулярна к любой прямой, лежащей в этой плоскости. а у р х Утверждение: Если прямая перпендикулярна плоскости, то она её пересекает.

Теоремы о связи между параллельностью прямых и их перпендикулярностью плоскости. Th 14 Если одна из двух параллельных прямых перпендикулярна плоскости, то и другая прямая, перпендикулярна этой плоскости. l 1 Доказательство Th 15 Если две прямые перпендикулярны плоскости, то они параллельны. l 1 l 2 b l 2 M B 1 Доказательство (следует из определения) B

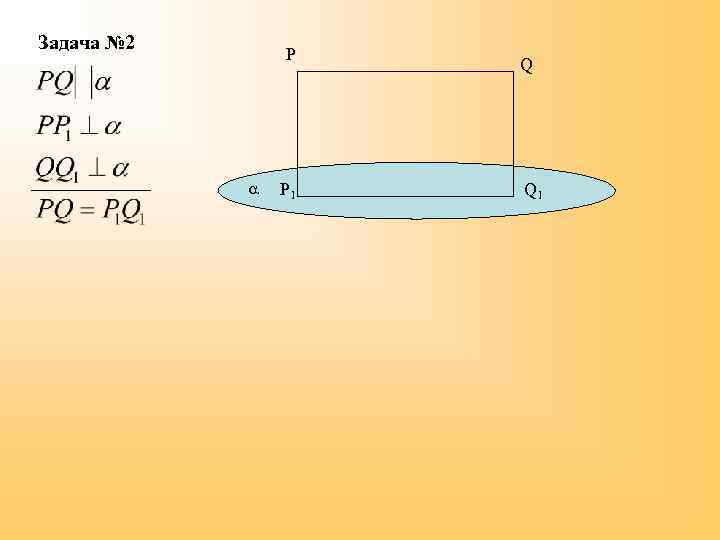Задача № 2 P P 1 Q Q 1

Признак перпендикулярности прямой и плоскости Th 13 Если прямая перпендикулярна каждой из двух пересекающихся прямых, лежащих в плоскости, то она перпендикулярна этой плоскости. Доказательство a А b c 1 m 1 b O 1 m c В Р Q L

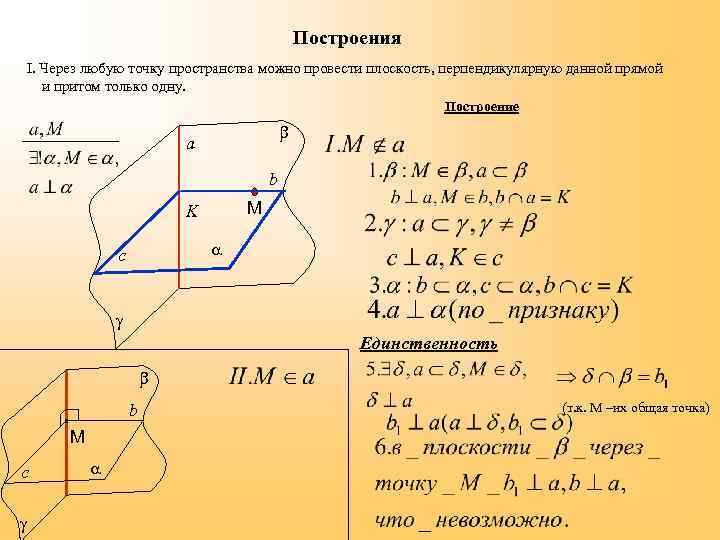Построения I. Через любую точку пространства можно провести плоскость, перпендикулярную данной прямой и притом только одну. Построение a b М K c Единственность b М с (т. к. М –их общая точка)

Построения II. Через любую точку пространства можно провести прямую, перпендикулярную данной плоскости и притом только одну. Построение M b Единственность a 1 a

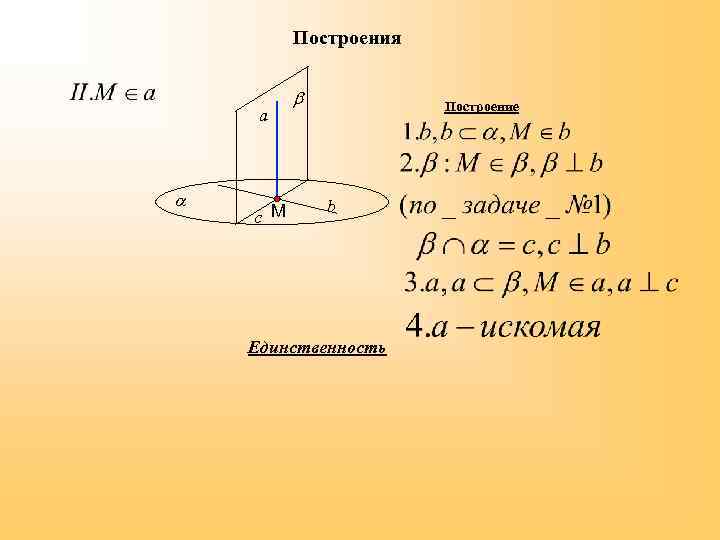Построения a c М Построение b Единственность

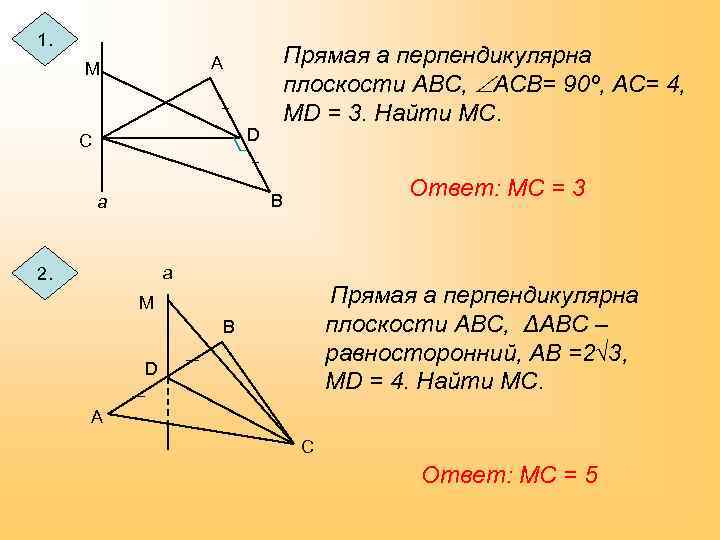1. Прямая а перпендикулярна плоскости АВС, АСВ= 90º, АС= 4, МD = 3. Найти МС. А М D С Ответ: МС = 3 В а а 2. Прямая а перпендикулярна плоскости АВС, ΔАВС – равносторонний, АВ =2√ 3, МD = 4. Найти МС. М В D А С Ответ: МС = 5

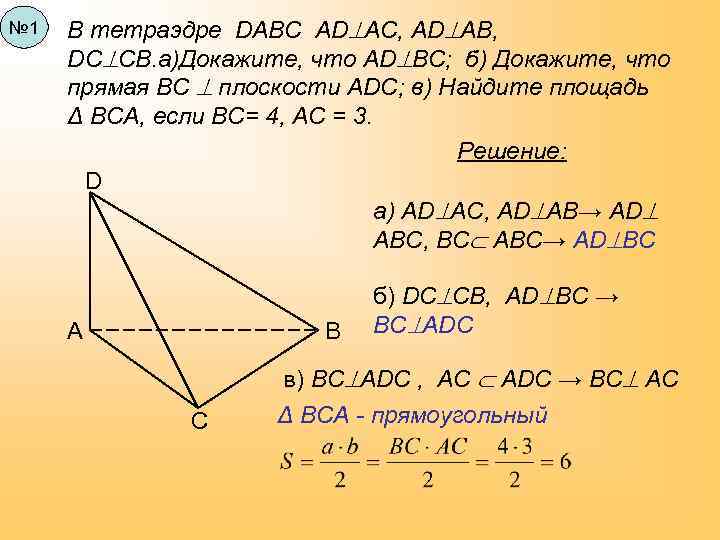№ 1 В тетраэдре DABC AD AC, AD AB, DC CB. а)Докажите, что AD ВC; б) Докажите, что прямая ВС плоскости АDС; в) Найдите площадь Δ ВСА, если ВС= 4, АС = 3. Решение: D а) AD AC, AD AB→ AD AВC, ВС АВС→ AD ВС А В С б) DC CB, AD ВС → ВС ADС в) ВС ADС , АС АDС → ВС АС Δ ВСА - прямоугольный

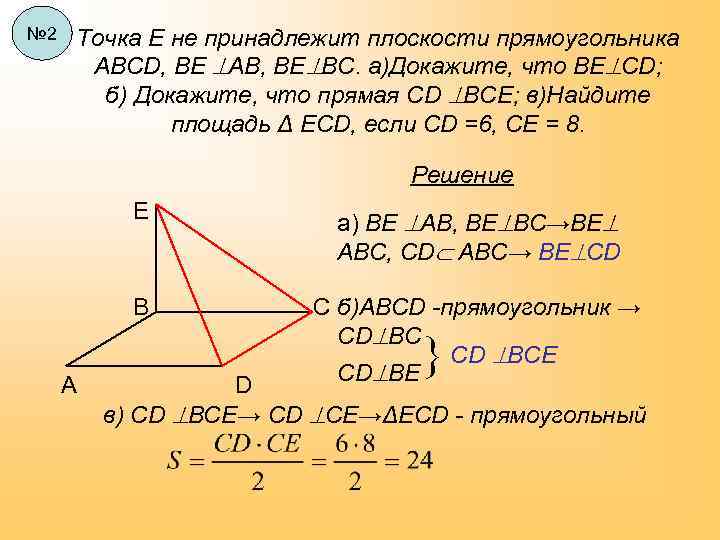№ 2 Точка Е не принадлежит плоскости прямоугольника АВСD, ВЕ AB, ВЕ ВС. а)Докажите, что ВЕ СD; б) Докажите, что прямая СD ВСЕ; в)Найдите площадь Δ ЕСD, если СD =6, СЕ = 8. Решение Е В А а) ВЕ AB, ВЕ ВС→ВЕ АВС, СD АВС→ ВЕ CD С б)АВСD -прямоугольник → СD BC СD ВСЕ СD ВЕ D в) СD ВСЕ→ СD СЕ→ΔЕСD - прямоугольный

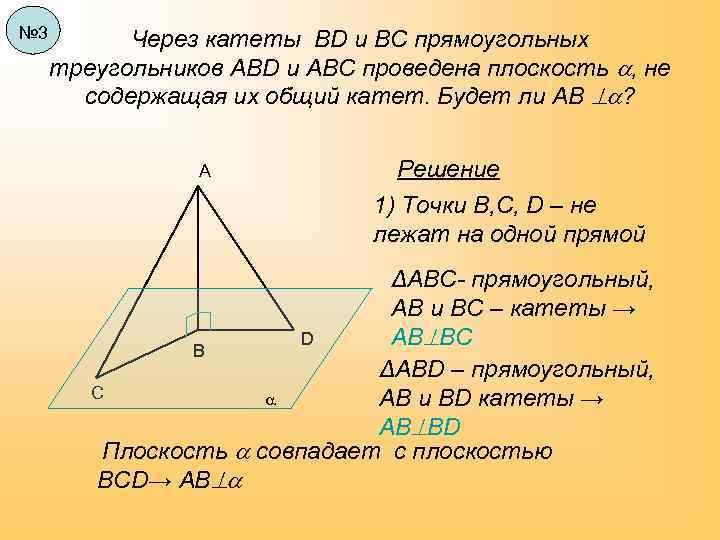№ 3 Через катеты ВD и ВС прямоугольных треугольников АВD и АВС проведена плоскость , не содержащая их общий катет. Будет ли АВ ? А Решение 1) Точки В, С, D – не лежат на одной прямой ΔABC- прямоугольный, АВ и ВС – катеты → AB BC D В ΔABD – прямоугольный, С AB и BD катеты → AB BD Плоскость совпадает с плоскостью BCD→ АВ

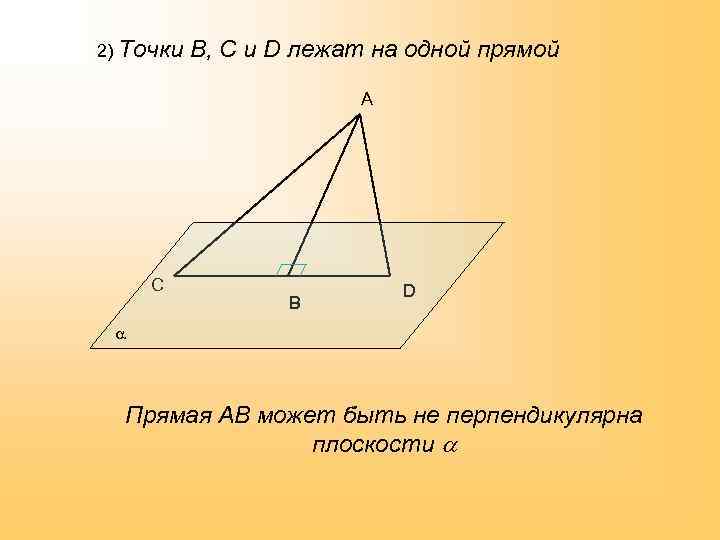2) Точки В, С и D лежат на одной прямой А С В D Прямая АВ может быть не перпендикулярна плоскости

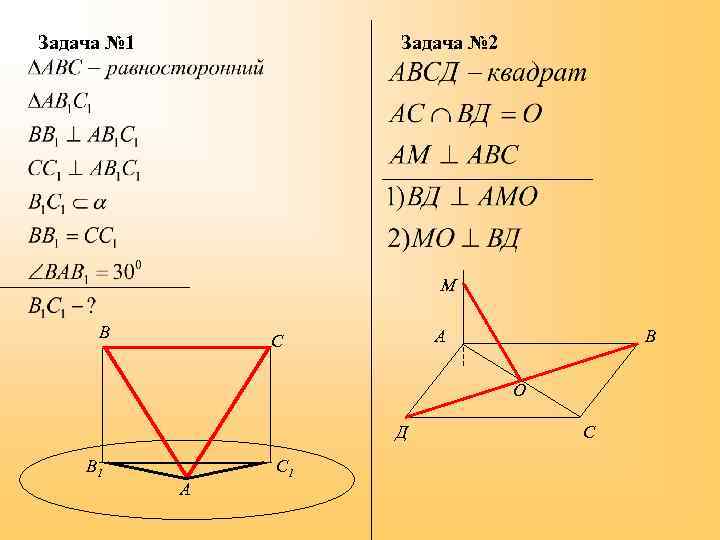Задача № 1 Задача № 2 М В А С В О Д В 1 А С 1 С

Домашнее задание Глава 2. § 1 стр. теорию учить, № 116, 123