Скачать презентацию Перпендикуляр к плоскости – отрезок, соединяющий данную точку Скачать презентацию Перпендикуляр к плоскости – отрезок, соединяющий данную точку

Геометрия.ppt

  • Количество слайдов: 18

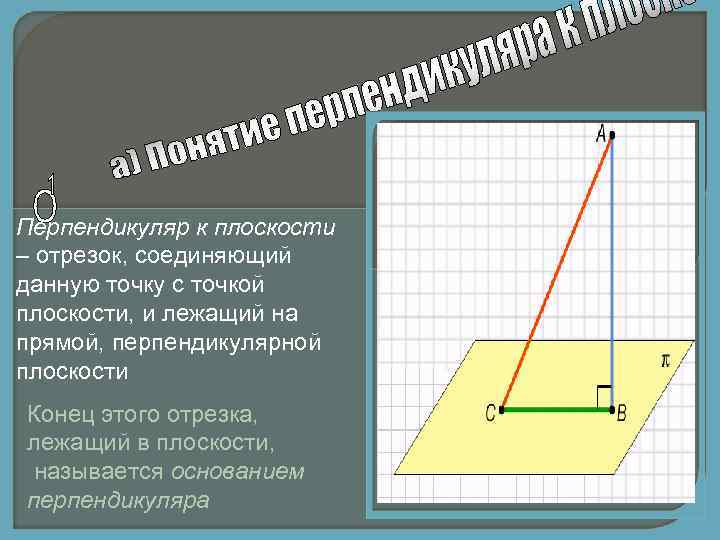
Перпендикуляр к плоскости – отрезок, соединяющий данную точку с точкой плоскости, и лежащий на Перпендикуляр к плоскости – отрезок, соединяющий данную точку с точкой плоскости, и лежащий на прямой, перпендикулярной плоскости Конец этого отрезка, лежащий в плоскости, называется основанием перпендикуляра

Расстояние от точки до плоскости – это длина перпендикуляра, проведенного из этой точки к Расстояние от точки до плоскости – это длина перпендикуляра, проведенного из этой точки к плоскости Расстояние между параллельными плоскостями – это расстояние от произвольной точки одной из параллельных плоскостей до другой плоскости Расстояние между прямой и параллельной ей плоскостью – это расстояние от произвольной точки прямой до плоскости Расстояние между скрещивающимися прямыми – это расстояние между одной из скрещивающихся прямых и плоскостью, проходящей через другую прямую параллельно первой

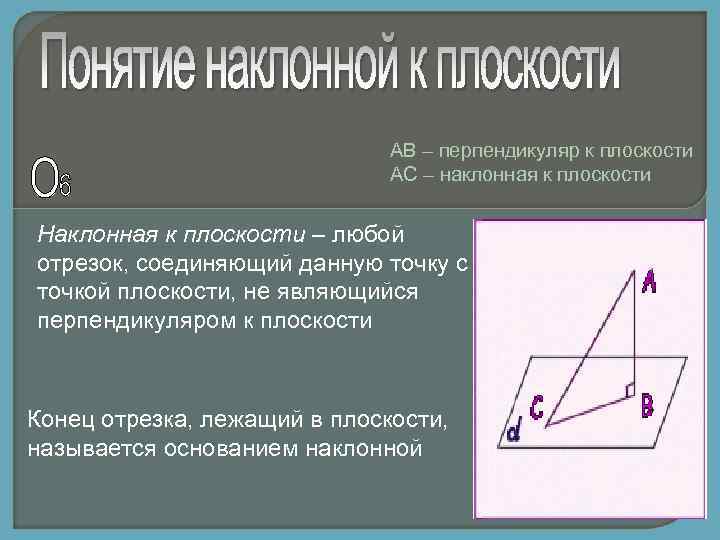АВ – перпендикуляр к плоскости АС – наклонная к плоскости Наклонная к плоскости – АВ – перпендикуляр к плоскости АС – наклонная к плоскости Наклонная к плоскости – любой отрезок, соединяющий данную точку с точкой плоскости, не являющийся перпендикуляром к плоскости Конец отрезка, лежащий в плоскости, называется основанием наклонной

Если прямая, проведенная на плоскости через основание наклонной, перпендикулярна ее проекции, то она перпендикулярна Если прямая, проведенная на плоскости через основание наклонной, перпендикулярна ее проекции, то она перпендикулярна наклонной. АВ – перпендикуляр плоскости альфа; АС – наклонная; с - прямая в плоскости альфа, проходящая через основание С.

Прямая с прямой АС 1. Проведем прямую СA 1, параллельную прямой АВ. Она плоскости Прямая с прямой АС 1. Проведем прямую СA 1, параллельную прямой АВ. Она плоскости альфа. 2. Проведем через прямые АВ и СA 1 плоскость бэта. Прямая с прямой СA 1. 3. Если прямая с прямой СВ, то она перпендикулярна плоскости бэта, а значит, и прямой АС.

Если прямая на плоскости перпендикулярна наклонной, то она перпендикулярна и проекции наклонной. АВ – Если прямая на плоскости перпендикулярна наклонной, то она перпендикулярна и проекции наклонной. АВ – перпендикуляр плоскости альфа; АС – наклонная; с - прямая в плоскости альфа, проходящая через основание С.

Прямая с прямой СВ 1. Если прямая с наклонной АС то она, будучи перпендикулярна Прямая с прямой СВ 1. Если прямая с наклонной АС то она, будучи перпендикулярна и прямой СA 1 перпендикулярна плоскости бэта => 2. Прямая с проекции наклонной СВ

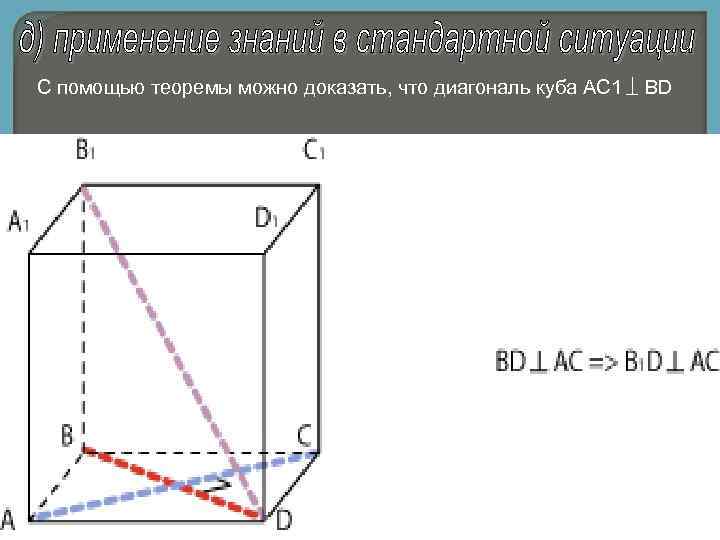С помощью теоремы можно доказать, что диагональ куба АС 1 BD С помощью теоремы можно доказать, что диагональ куба АС 1 BD

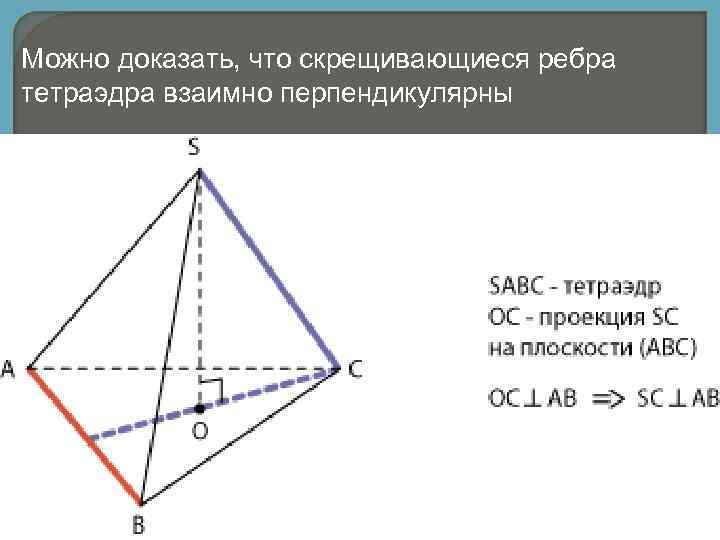Можно доказать, что скрещивающиеся ребра тетраэдра взаимно перпендикулярны Можно доказать, что скрещивающиеся ребра тетраэдра взаимно перпендикулярны

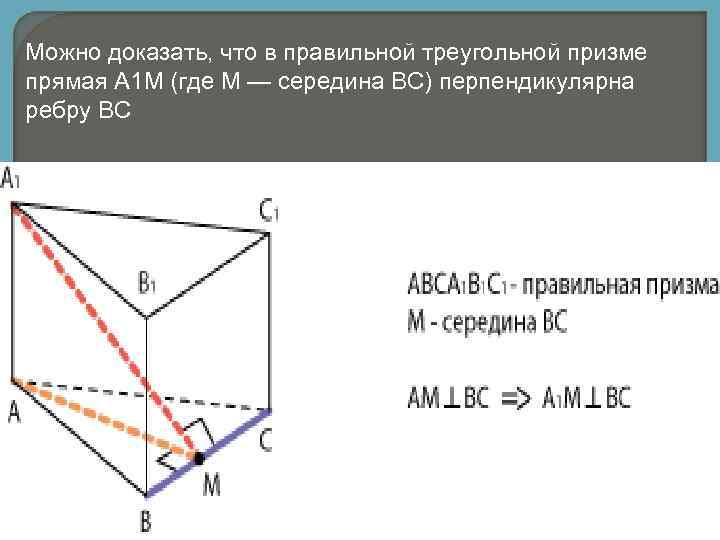Можно доказать, что в правильной треугольной призме прямая А 1 М (где М — Можно доказать, что в правильной треугольной призме прямая А 1 М (где М — середина ВС) перпендикулярна ребру ВС

АМ=МС АВ=ВС 1) МВА и МВС – прямоугольные 2) а) МВ – общий катет АМ=МС АВ=ВС 1) МВА и МВС – прямоугольные 2) а) МВ – общий катет б) АМ=МС 3) МВА = МВС => 4) АВ = ВС

АВ=ВС АМ=МС 1) МВА и МВС – прямоугольные 2) а) МВ – общий катет АВ=ВС АМ=МС 1) МВА и МВС – прямоугольные 2) а) МВ – общий катет б) АВ=ВС 3) МВА = МВС => 4) АМ = МС

АМ>МС АВ>ВС 1) 2) 3) АМ>МС АВ>ВС 1) 2) 3)

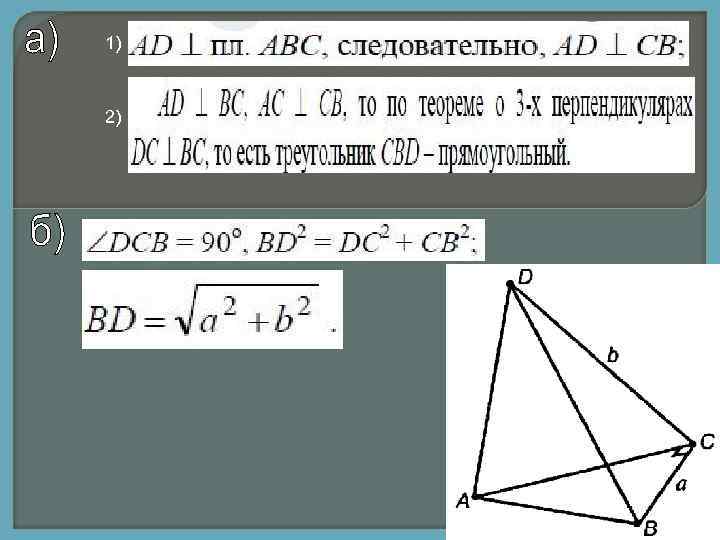
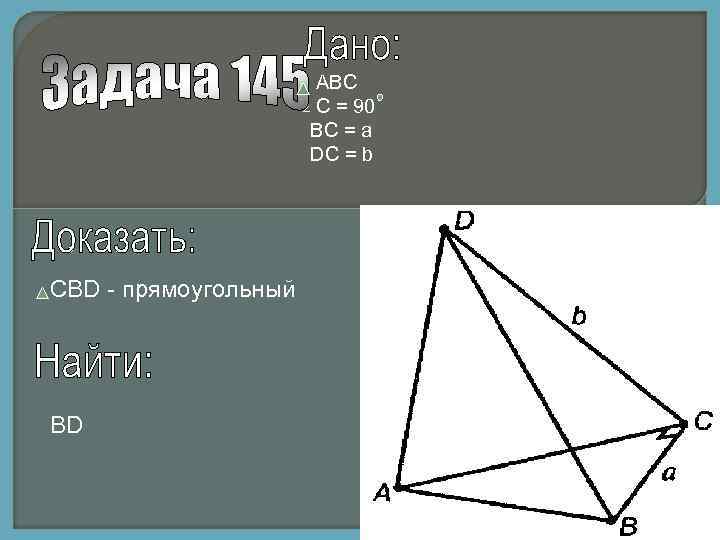АВС С = 90 ВС = а DC = b CBD - прямоугольный АВС С = 90 ВС = а DC = b CBD - прямоугольный BD

1) 2) 1) 2)