Периодические несинусоидальные токи Лекция 5 Разложение периодических

Периодические несинусоидальные токи Лекция 5

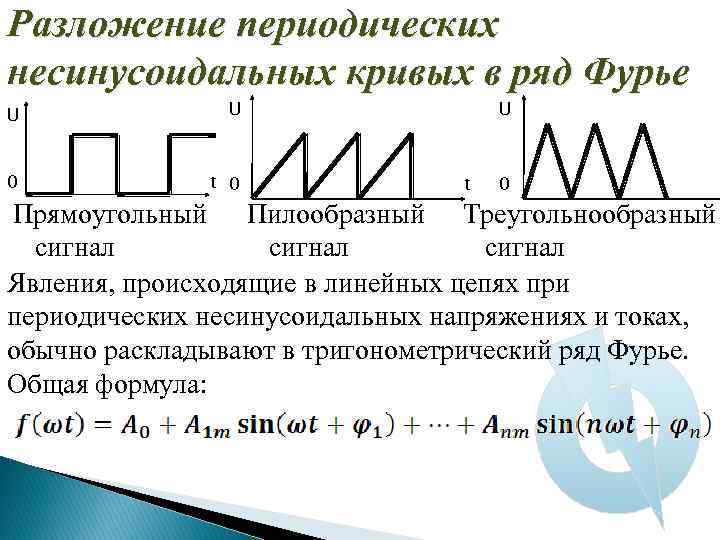Разложение периодических несинусоидальных кривых в ряд Фурье U U 0 t 0 U t 0 Прямоугольный Пилообразный Треугольнообразный сигнал Явления, происходящие в линейных цепяx при периодических несинусоидальных напряжениях и токах, обычно раскладывают в тригонометрический ряд Фурье. Общая формула:

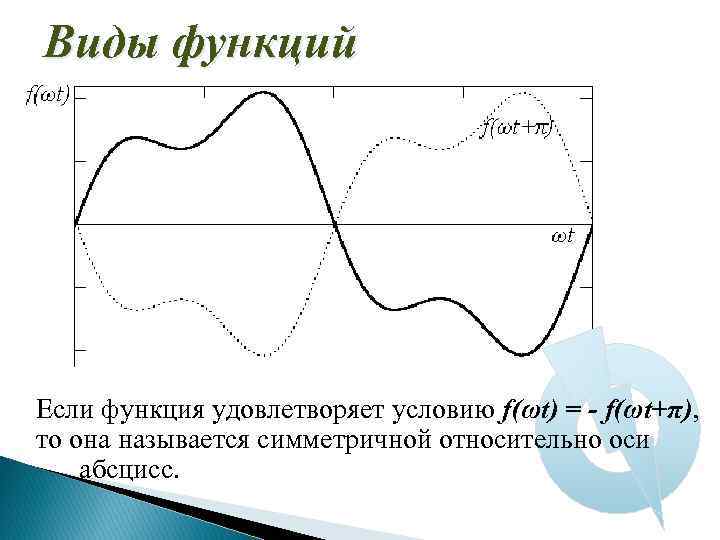Виды функций Если функция удовлетворяет условию f(ωt) = - f(ωt+π), то она называется симметричной относительно оси абсцисс.

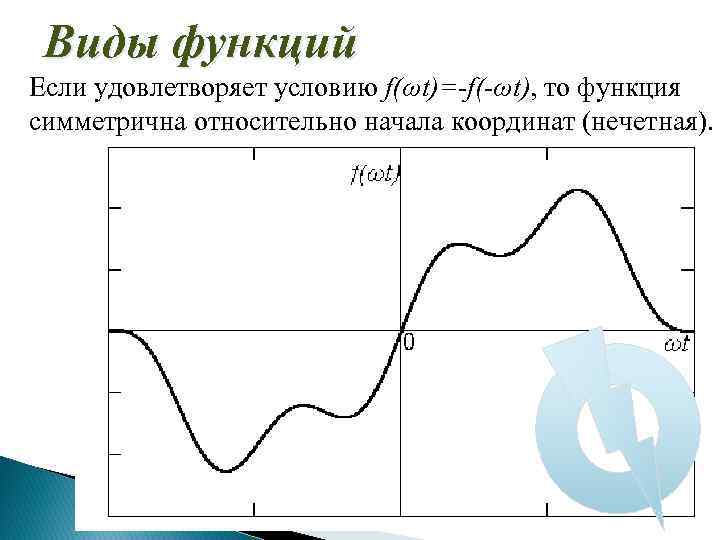Виды функций Если удовлетворяет условию f(ωt)=-f(-ωt), то функция симметрична относительно начала координат (нечетная).

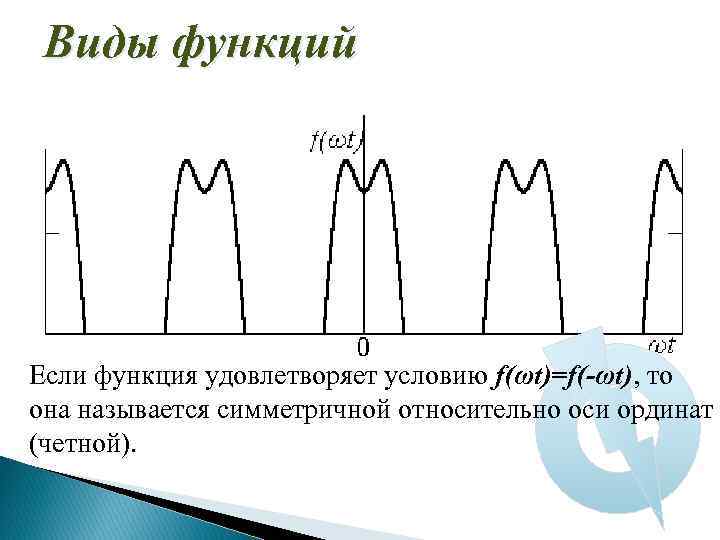Виды функций Если функция удовлетворяет условию f(ωt)=f(-ωt), то она называется симметричной относительно оси ординат (четной).

Мощность несинусоидального тока Активная мощность – средняя мощность за период Т: Действующее значение активной мощности: Где начальные фазы синусоидальных тока и напряжения. Активная мощность периодического несинусоидального тока равна сумме активных мощностей отдельных гармоник. Постоянная составляющая рассматривается как нулевая гармоника с .

Мощность несинусоидального тока Полная мощность S определяется как произведение действующих несинусоидальных значений тока и напряжения: Понятие «реактивная мощность» для цепей с несинусоидальными токами, как правило, не используют. Однако формально можно ввести его как сумму реактивных мощностей отдельных гармоник:

Мощность несинусоидального тока В отличие от синусоидальных токов для несинусоидальных выполняется неравенство: где Т – мощность искажения, которая зависит от степени различия форм кривых несинусоидальных напряжений и тока. При чисто активном сопротивлении цепи несинусоидального тока кривые напряжения и тока подобны (Т=0) и Q=0, S=P.

Переходные процессы I закон коммутации: ток в ветви с индуктивным Переходными называют процессы, которые проходят элементом в начальный момент времени после при изменении режима работы в электрических цепях. коммутации имеет то же значение, какое он имел Например, при включении/выключении источника непосредственно перед коммутацией, а затем с этого питания, изменении параметров элементов. значения начинает плавно изменяться. Закон Для рассмотрения особенностей переходных процессов записывают в виде i. L(0 -) = i. L(0+), считая, что используют 2 закона коммутации. коммутация происходит мгновенно в момент t = 0. II закон коммутации: напряжение на емкостном элементе в начальный момент после коммутации имеет то же значение, какое оно имело непосредственно перед коммутацией, а затем с этого значения начинает плавно изменяться: UC(0 -) = UC(0+).

Переходный, принужденный и свободный режимы Пусть в некоторой цепи внезапно изменяется сопротивление. До коммутации в цепи существовали сопротивления R 0 и R, после коммутации остается только R. Требуется определить переходный ток i. Электрическое состояние схемы после коммутации Если это уравнение продифференцировать по времени получим линейное дифференциальное уравнение описывается интегродифференциальным уравнением, второго порядка, у которого в качестве постоянных записанным на основании II закона Кирхгофа для коэффициентов выступают параметры цепи или их мгновенных значений токов и напряжений: комбинации:

Поскольку в правой части дифференциальных уравнений, описывающих электрическое состояние цепей, обычно находится напряжение (или ток) источника (внешняя вынуждающая сила), то частное решение находят из анализа установившегося режима после коммутации. Отсюда этот режим называют принужденным и соответственно токи или напряжения, найденные в данном режиме, называют принужденными Общее решение описывает переходной процесс без источника (е=0), т. е. протекающий за счёт накопленной энергии в индуктивности и ёмкости и имеющий одинаковый вид для любого переходного процесса. Такой режим называется свободным

Существуют различные методы решения однородного дифференциального уравнения: Классический метод анализа переходных процессов заключается в непосредственном интегрировании дифференциальных уравнений. Решение находят в виде суммы экспонент: где число слагаемых равно порядку дифференциального уравнения. Ток в соответствии с принципом суперпозиции равен сумме установившегося (принужденного) и свободного токов: i = iу + iсв.

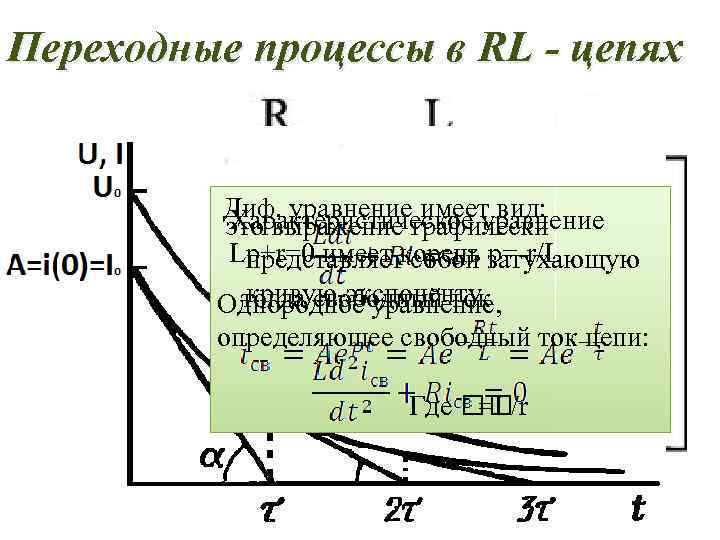Переходные процессы в RL - цепях Диф. уравнение имеет вид: Характеристическое уравнение это выражение графически Lp+r=0 имеет корень p=-r/L представляет собой затухающую кривую-экспоненту тогда свободный ток Однородное уравнение, определяющее свободный ток цепи: Где =L/r

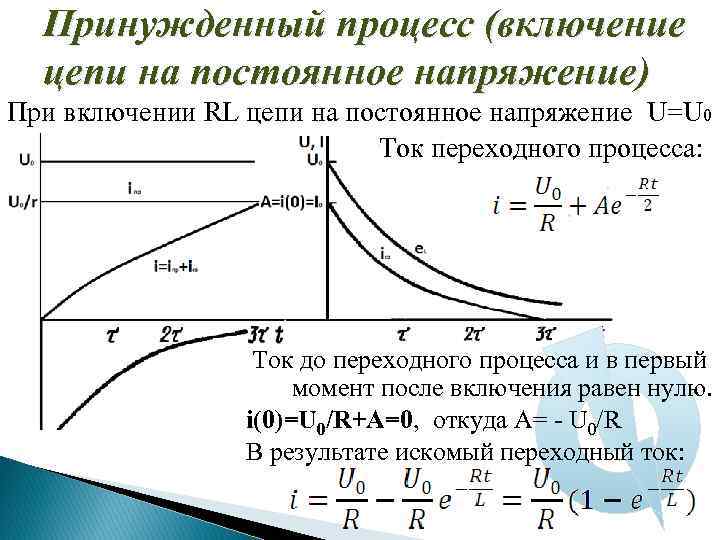Принужденный процесс (включение цепи на постоянное напряжение) При включении RL цепи на постоянное напряжение U=U 0 Ток переходного процесса: Ток до переходного процесса и в первый момент после включения равен нулю. i(0)=U 0/R+A=0, откуда А= - U 0/R В результате искомый переходный ток:

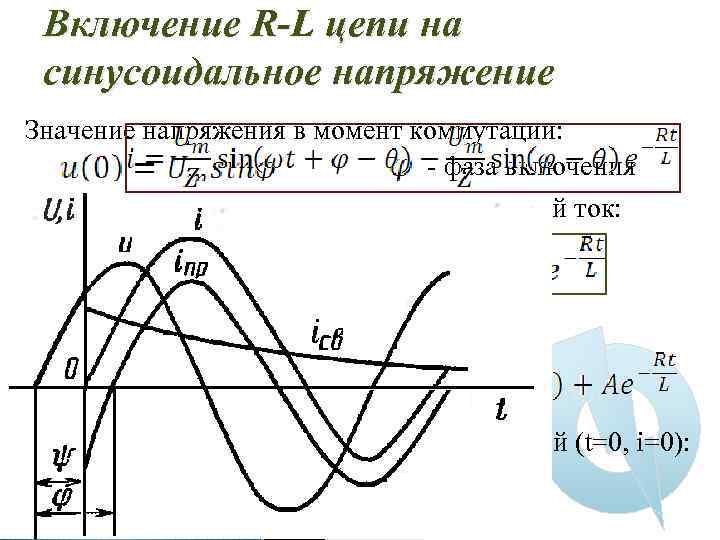Включение R-L цепи на синусоидальное напряжение Значение напряжения в момент коммутации: - фаза включения Принужденный ток в цепи: Свободный ток: Переходный ток: Найдем постоянную А из начальных условий (t=0, i=0):

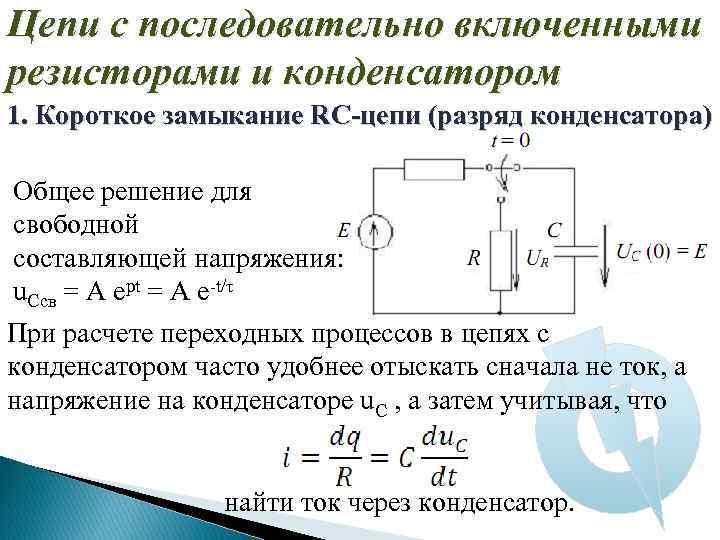Цепи с последовательно включенными резисторами и конденсатором 1. Короткое замыкание RC-цепи (разряд конденсатора) Общее решение для свободной составляющей напряжения: u. Cсв = A ept = A e-t/τ При расчете переходных процессов в цепях с конденсатором часто удобнее отыскать сначала не ток, а напряжение на конденсаторе u. C , а затем учитывая, что найти ток через конденсатор.

Цепи с последовательно включенными резисторами и конденсатором Запишем уравнение по второму закону Кирхгофа в виде: Характеристическое уравнение имеет вид: RCp + 1 = 0 Общее решение для свободного напряжения: u. Cсв = A ept = A e-t/τ где: τ = RC. С учетом нулевого значения установившегося напряжения получим напряжение на конденсаторе: u. C = U 0 e-t/τ Переходный ток в цепи: Знак минус свидетельствует о том, что ток разрядки имеет направление противоположное напряжению на конденсаторе.

Графики изменения тока и напряжений на емкости и сопротивлении. С энергетической точки зрения переходный процесс характеризуется переходом энергии электрического поля конденсатора в тепловую энергию в резисторе. Следует отметить; что сопротивление резистора влияет не на количество выделенной теплоты, а на начальное значение тока и длительность разряда. В самом деле:

Цепи с последовательно включенными резисторами и конденсатором 2. Включение RC- цепи на постоянное напряжение При включении этой цепи конденсатор будет заряжаться до принужденного Ток при зарядке конденсатора: напряжения uc=U 0. Свободное напряжение: Переходное напряжение: Ток спадает тем медленнее, чем больше постоянная времени цепи τ, то Напряжение до коммутации: есть чем медленнее затухает свободное напряжение на конденсаторе.

Цепи с последовательно включенными резисторами и конденсатором 2. Включение RC- цепи на синусоидальное напряжение Напряжение источника: u=Umsin(ωt+φ) Определим постоянную А: (uc=0) u. Cсв = A e-t/τ, Переходный ток равен: τ = RC.

Если в момент включения мгновенное значение установившегося напряжение на конденсаторе равно нулю (ψ–φ–π/2=0), то и свободная составляющая напряжения равна нулю. В цепи установившийся режим (рис. а). Если в момент включения напряжение на конденсаторе имеет наибольшее значение (ψ–φ-π/2=π/2), то переходное напряжение достигает максимального значения и может приблизиться к удвоенной амплитуде установившегося напряжения, но не превысит его (рис. в).

Включение контура RLC на постоянное напряжение Апериодический процесс: Между разрядом конденсатора и включением на постоянное напряжение RLC-контура существует аналогия. В обоих случаях, установившаяся составляющая тока равна нулю. Установившееся напряжение на конденсаторе u. Cу = U. Следовательно, начальное значение свободной составляющей напряжения на конденсаторе равно -U.

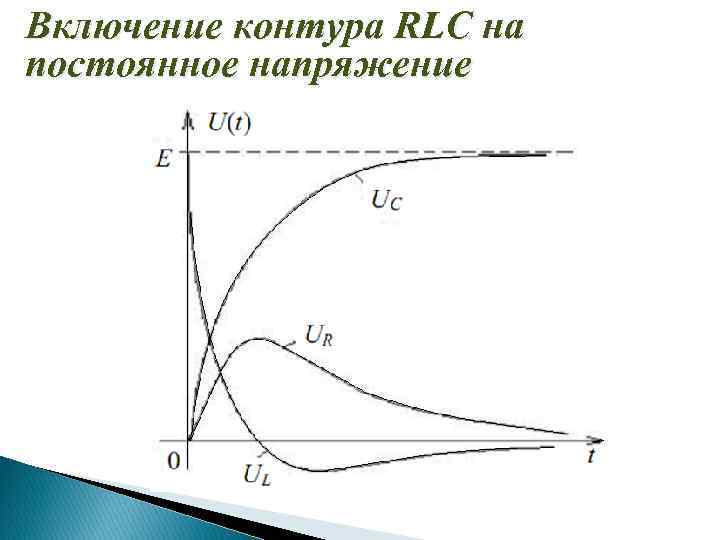Включение контура RLC на постоянное напряжение