Performance guarantees for hierarchical clustering Sanjoy Dasgupta Philip

Performance guarantees for hierarchical clustering Sanjoy Dasgupta Philip Long University of California, San Diego Genomics Institute of Singapore

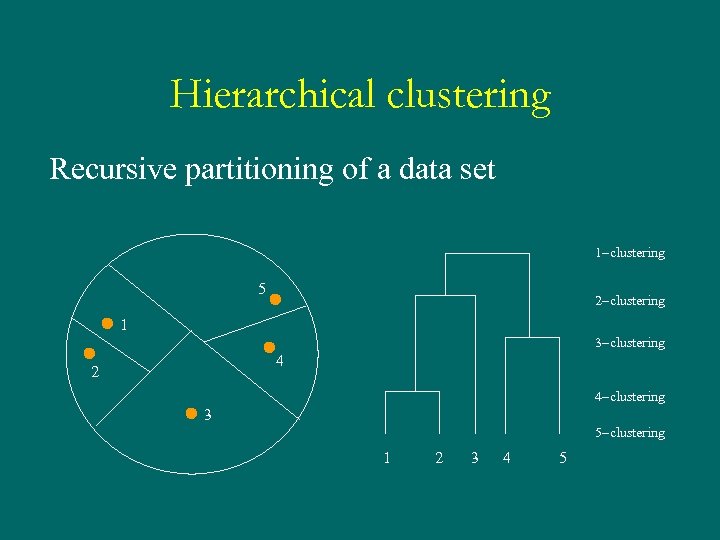Hierarchical clustering Recursive partitioning of a data set 1 -clustering 5 2 -clustering 1 3 -clustering 4 2 4 -clustering 3 5 -clustering 1 2 3 4 5

Popular form of data analysis • No need to specify number of clusters • Can view data at many levels of granularity, all at the same time • Simple heuristics for constructing hierarchical clusterings

Applications • Has long been used by biologists and social scientists • A standard part of the statistician’s toolbox since the 60 s or 70 s • Recently: common tool for analyzing gene expression data

Performance guarantees There are many simple greedy schemes for constructing hierarchical clusterings. But are these resulting clusterings any good? Or are they pretty arbitrary?

One basic problem In fact, the whole enterprise of hierarchical clustering could use some more justification. e. g.

An existence question Must there always exist a hierarchical clustering which is close to optimal at every level of granularity, simultaneously? [I. e. , such that for all k, the induced kclustering is close to the best k-clustering? ]

What is the best k-clustering? The k-clustering problem. Input: data points in a metric space; k Output: a partition of the points into k clusters C 1, …, Ck with centers m 1, . . . , mk Goal: minimize cost of the clustering

Cost functions for clustering Two cost functions which are commonly used: Maximum radius (k-center) max {d(x, mi): i = 1…k, x in Ci} Average radius (k-median) avg {d(x, mi): i = 1…k, x in Ci} Both yield NP-hard optimization problems, but have constant-factor approximation algorithms.

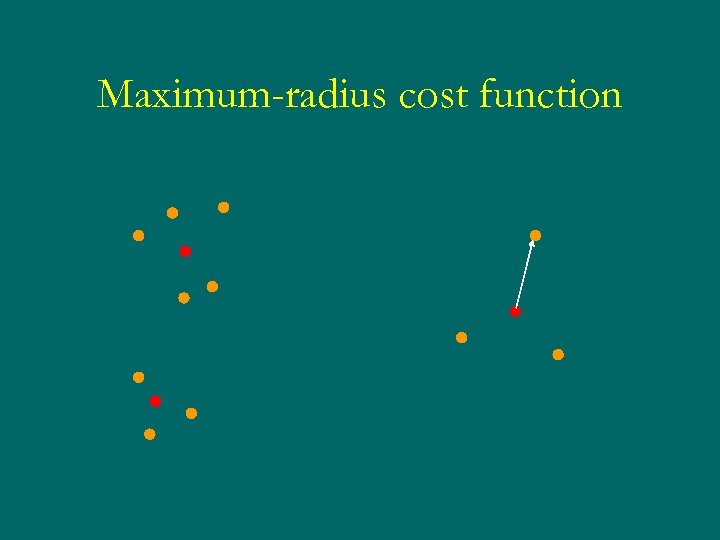Maximum-radius cost function

Our main result Adopt the maximum-radius cost function. Our algorithm returns a hierarchical clustering such that for every k, the induced k-clustering is guaranteed to be within a factor eight of optimal.

Standard heuristics • The standard heuristics for hierarchical clustering are greedy and work bottom-up: single-linkage, average-linkage, complete-linkage • Their k-clusterings can be off by a factor of: -- at least log 2 k (average-, complete-linkage); -- at least k (single-linkage). • Our algorithm is similar in efficiency and simplicity, but works top-down.

A heuristic for k-clustering [Hochbaum and Shmoys, 1985] Eg. k = 4. 3 2 1 R 4 This 4 -clustering has cost R 2 OPT 4

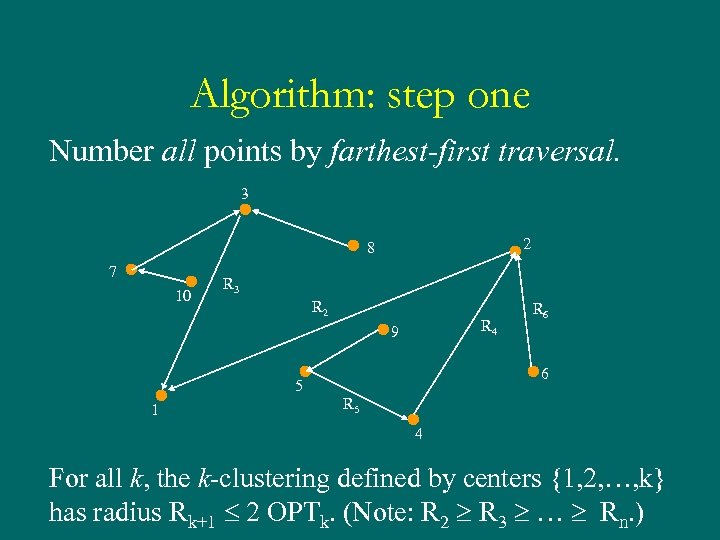Algorithm: step one Number all points by farthest-first traversal. 3 2 8 7 10 R 3 R 2 R 4 9 5 1 R 6 6 R 5 4 For all k, the k-clustering defined by centers {1, 2, …, k} has radius Rk+1 2 OPTk. (Note: R 2 R 3 … Rn. )

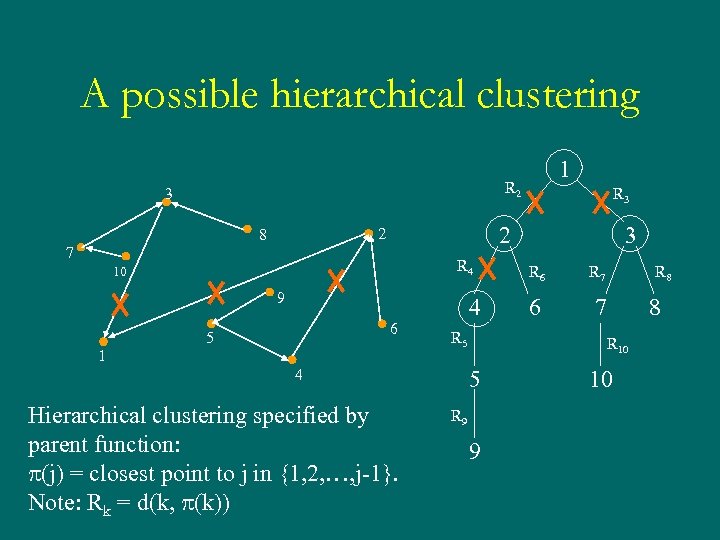A possible hierarchical clustering R 2 3 7 R 4 10 9 6 5 R 3 2 2 8 1 1 4 R 5 Hierarchical clustering specified by parent function: p(j) = closest point to j in {1, 2, …, j-1}. Note: Rk = d(k, p(k)) R 6 R 7 6 R 8 7 8 R 10 5 4 3 R 9 9 10

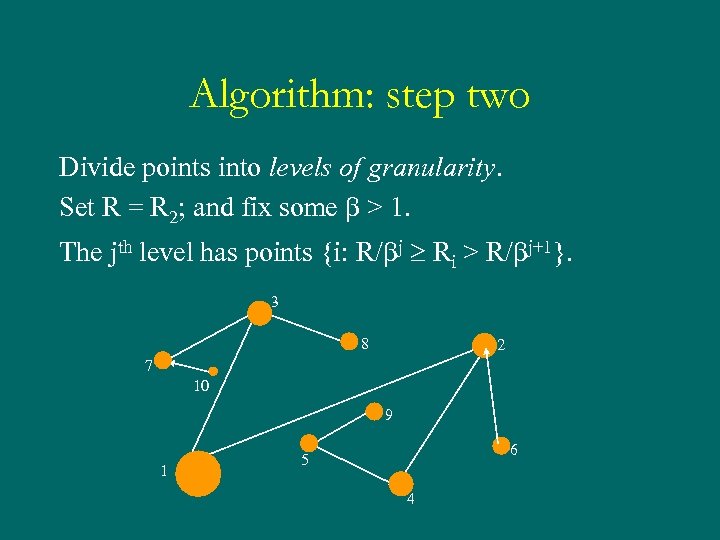Algorithm: step two Divide points into levels of granularity. Set R = R 2; and fix some b > 1. The jth level has points {i: R/bj Ri > R/bj+1}. 3 8 2 7 10 9 1 6 5 4

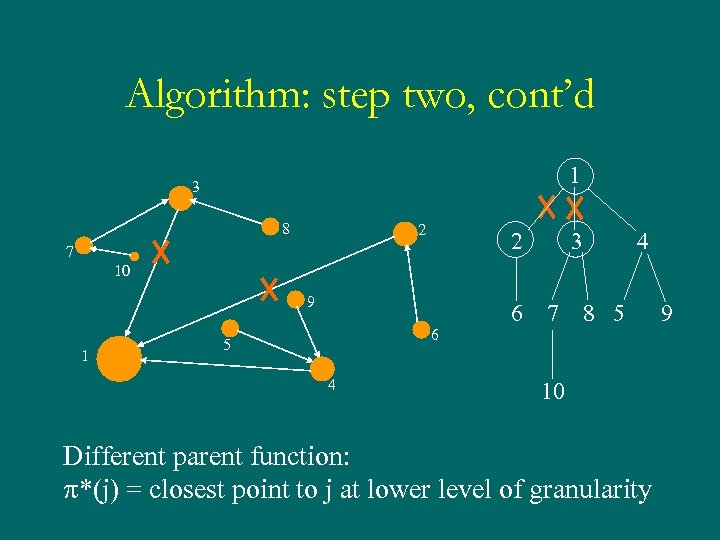Algorithm: step two, cont’d 1 3 8 2 2 7 3 4 10 9 1 6 5 4 6 7 8 5 10 Different parent function: p*(j) = closest point to j at lower level of granularity 9

Algorithm: summary 1. 2. 3. 4. Number the points by farthest-first traversal; note the values Ri = d(i, {1, 2, …, i-1}). Choose R = a R 2. L(0) = {1}; for j > 0, L(j) = {i: R/bj-1 Ri > R/bj}. If point i is in L(j), p*(i) = closest point to i in L(0), …. , L(j-1). Theorem: Fix a=1, b=2. If the data points lie in a metric space, then for all k simultaneously, the induced kclustering is within a factor eight of optimal.

Randomization trick Pick a from the distribution b. U[0, 1]. Set b = e. Then for all k, the induced k-clustering has expected cost at most 2 e 5. 44 times optimal. Thanks to Rajeev Motwani for suggesting this.

What does a constant-factor approximation mean? Prevent the worst.

Standard agglomerative heuristics 1. Initially each point is its own cluster. 2. Repeatedly merge the two “closest” clusters. Need to define distance between clusters… Single-linkage: distance between closest pair of points Average-linkage: distance between centroids Complete-linkage: distance between farthest pair

Single-linkage clustering Chaining effect. 1 - jd 1 2 3 … j j+1 … n The k-clustering will have diameter about n-k, instead of n/k. Therefore: off by a factor of k.

Average-linkage clustering Points in d-dimensional space, d = log 2 k, under an l 1 metric. Final radius should be 1, instead is d. Therefore: off by a factor of log 2 k.

Complete-linkage clustering Can similarly construct a bad case… Off by a factor of at least log 2 k.

Summary There is a basic existence question about hierarchical clustering which needs to be addressed: must there always exist a hierarchical clustering in which, for each k, the induced k-clustering is close to optimal? It turns out the answer is yes.

Summary, cont’d In fact, there is a simple, fast algorithm to construct such hierarchical clusterings. Meanwhile, the standard agglomerative heuristics do not always produce close-tooptimal clusterings.

Where next? 1. Reduce the approximation factor. 2. Other cost functions for clustering. 3. For average- and complete-linkage, is the log k lower bound also an upper bound? 4. Local improvement procedures for hierarchical clustering?