Перевод восьмеричных и шестнадцатеричных чисел в двоичную систему

Перевод восьмеричных и шестнадцатеричных чисел в двоичную систему и наоборот

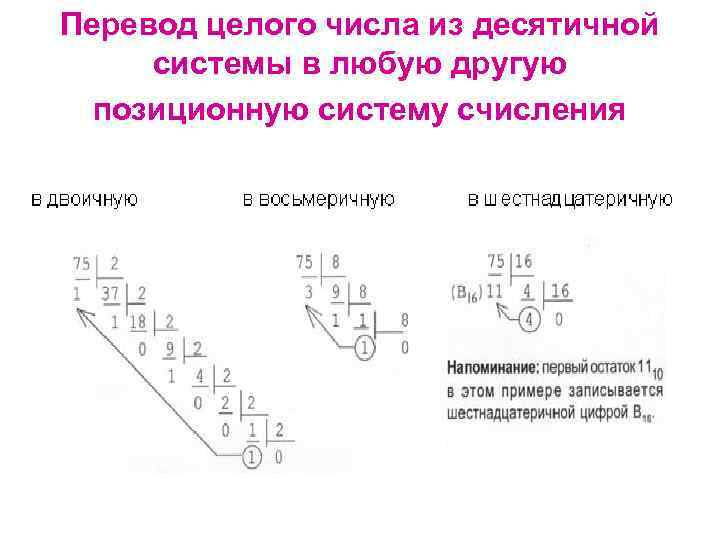Перевод целого числа из десятичной системы в любую другую позиционную систему счисления

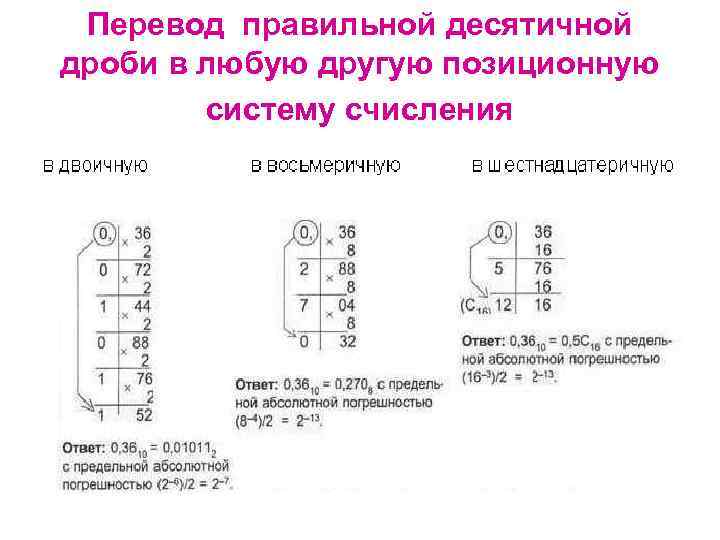Пеpевод правильной десятичной дроби в любую другую позиционную систему счисления

Логические основы компьютеров Алгебра логики - это раздел математики, изучающий высказывания, рассматриваемые со стороны их логических значений (истинности или ложности) и логических операций над ними. Логическое высказывание - это любое повествовательное пpедложение, в отношении которого можно однозначно сказать, истинно оно или ложно. Высказывательная форма - это повествовательное предложение, которое прямо или косвенно содержит хотя бы одну переменную и становится высказыванием, когда все переменные замещаются своими значениями.

Логические связки Слова и словосочетания "не", "или", "если. . . , то", "тогда и только тогда" позволяют из уже заданных высказываний строить новые высказывания. НЕ Операция, выражаемая словом "не", называется отрицанием и обозначается чертой над высказыванием или знаком. И Операция, выражаемая связкой "и", называется конъюнкцией (лат. cоnjunctiо - соединение) или логическим умножением и обозначается точкой & или знаками. ИЛИ Операция, выражаемая связкой "или" (в неисключающем смысле этого слова), называется дизъюнкцией (лат. disjunctiо разделение) или логическим сложением и обозначается знаком v (или плюсом). ЕСЛИ-ТО Операция, выражаемая связками "если. . . , то", "из. . . следует", ". . . влечет. . . ", называется импликацией (лат. implicо - тесно связаны) и обозначается знаком.

Логические связки РАВНОСИЛЬНО Операция, выражаемая связками "тогда и только тогда", "необходимо и достаточно", ". . . равносильно. . . ", называется эквиваленцией или двойной импликацией и обозначается знаком или ~. Импликацию можно выразить через дизъюнкцию и отрицание: Эквиваленцию можно выразить через отрицание, дизъюнкцию и конъюнкцию: Порядок выполнения логических операций следующий - сначала выполняется операция отрицания ("не"), затем конъюнкция ("и"), после конъюнкции - дизъюнкция ("или") и в последнюю очередь – импликация. Иной порядок задается круглыми скобками.

Логические формулы Определение логической формулы: • Всякая логическая переменная и символы "истина" ("1") и "ложь" ("0") - формулы. • Если А и В - формулы, то , - формулы. • Никаких других формул в алгебре логики нет. Логические формулы могут быть: • выполнимыми, т. е. принимать значения 1 или 0 в зависимости от значений входящих в них переменных; • тождественно истинными или тавтологиями, при любых значениях входящих в них переменных равны 1; • тождественно ложными или противоречиями, при любых значениях входящих в них переменных равными 0; • равносильными – принимать одинаковые значения при одинаковых значениях входящих в них переменных.

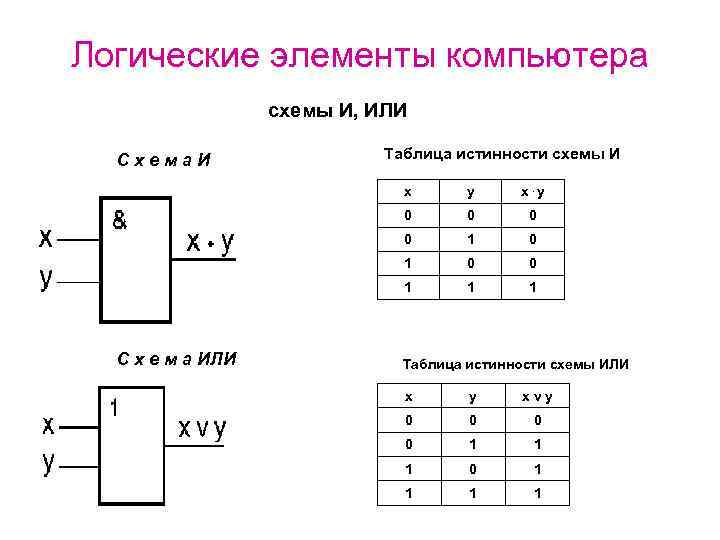Логические элементы компьютера схемы И, ИЛИ Схема. И Таблица истинности схемы И x x. y 0 0 1 С х е м а ИЛИ y 1 1 Таблица истинности схемы ИЛИ x y x v y 0 0 1 1 1 0 1 1

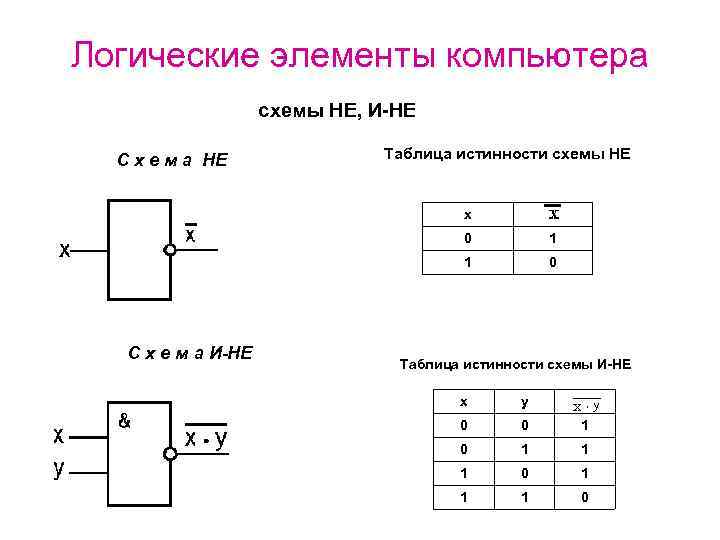Логические элементы компьютера схемы НЕ, И-НЕ С х е м а НЕ Таблица истинности схемы НЕ x 0 1 С х е м а И-НЕ 1 0 Таблица истинности схемы И-НЕ x y 0 0 1 1 1 0

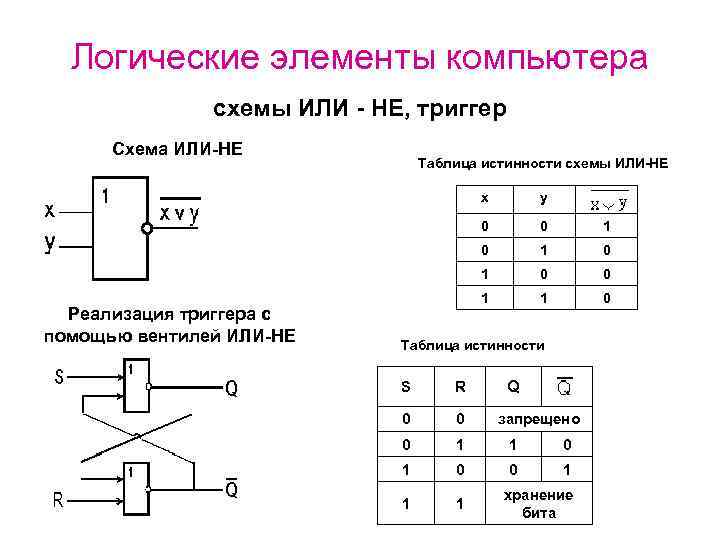Логические элементы компьютера схемы ИЛИ - НЕ, триггер Схема ИЛИ-НЕ Таблица истинности схемы ИЛИ-НЕ x 0 0 1 0 1 Реализация триггера с помощью вентилей ИЛИ-НЕ y 0 0 1 1 0 Таблица истинности Q S R 0 0 0 1 1 1 запрещено хранение бита

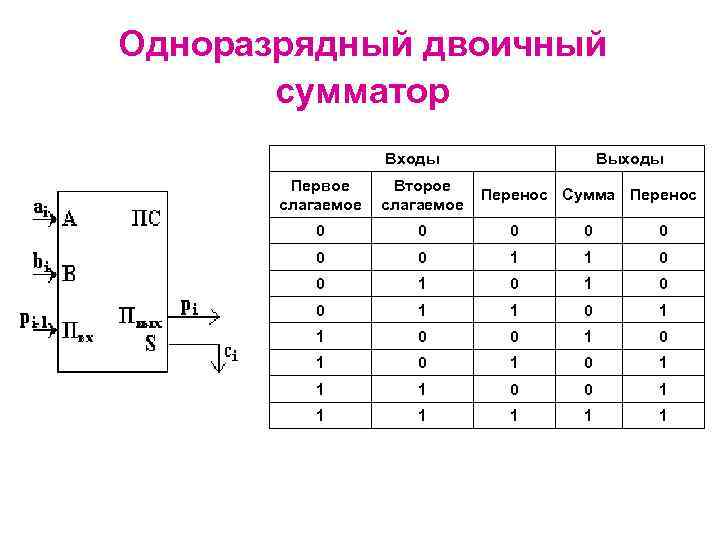Одноразрядный двоичный сумматор Входы Выходы Первое слагаемое Второе слагаемое 0 0 0 0 1 1 0 0 1 0 1 1 1 0 0 1 1 1 Перенос Сумма Перенос

Каскад сумматоров

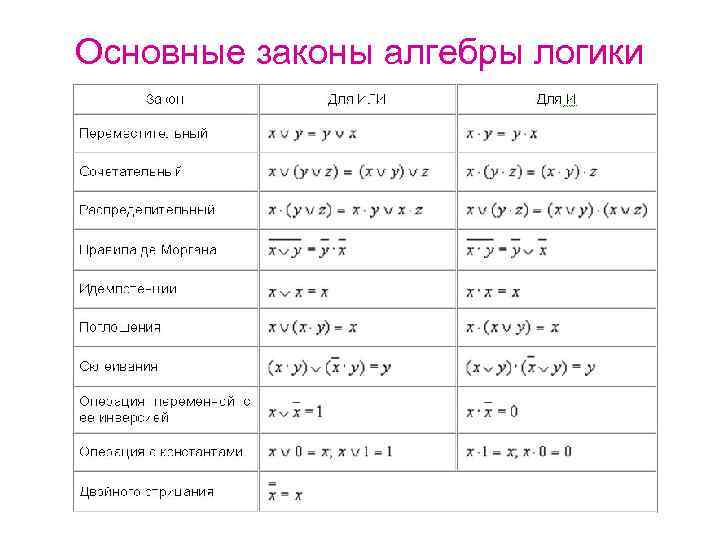Основные законы алгебры логики

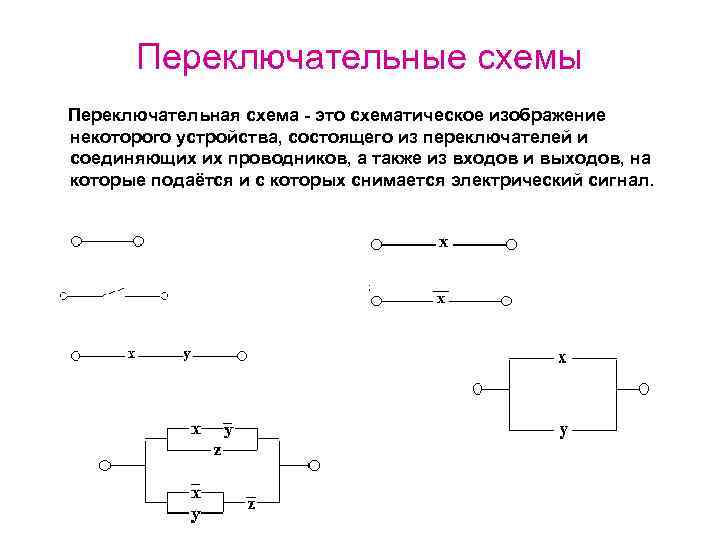Переключательные схемы Переключательная схема - это схематическое изображение некоторого устройства, состоящего из переключателей и соединяющих их проводников, а также из входов и выходов, на которые подаётся и с которых снимается электрический сигнал. ;

Синтез и анализ переключательных схем СИНТЕЗ СХЕМЫ по заданным условиям ее работы сводится к следующим трём этапам: • составлению функции проводимости по таблице истинности, отражающей эти условия; • упрощению этой функции; • построению соответствующей схемы. АНАЛИЗ СХЕМЫ сводится к • определению значений её функции проводимости при всех возможных наборах входящих в эту функцию переменных. • получению упрощённой формулы.

Упрощение переключательных схем • Две переключательные схемы называются равносильными, если через одну из них проходит ток тогда и только тогда, когда он проходит через другую (при одном и том же входном сигнале). • Из двух равносильных схем более простой считается та схема, функция проводимости которой содержит меньшее число логических операций или переключателей.

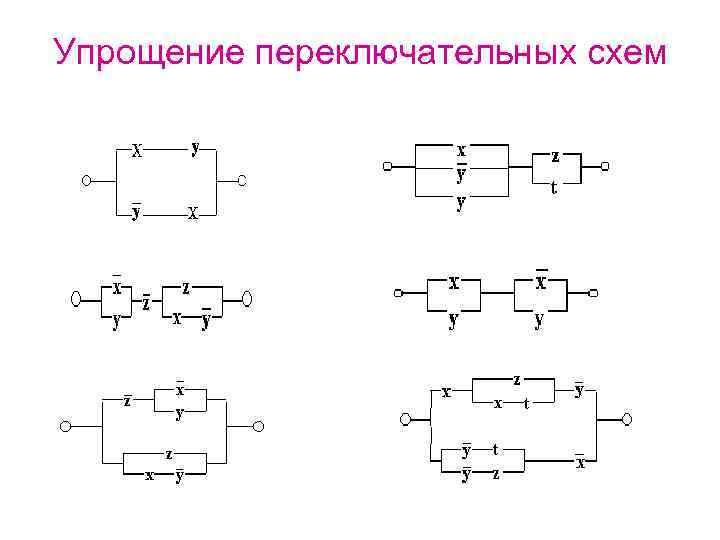Упрощение переключательных схем