Перетворення графіків тригонометричних функцій Основні типи перетворень

Перетворення графіків тригонометричних функцій

Основні типи перетворень Функція Тип перетворення Y= -f(x) Симетрія графіка функції y=f(x) відносно вісі ОХ Y= f(-x) Симетрія графіка функції y=f(x) відносно вісі ОУ Y=f(x+k) Паралельне перенесення графіка функції y=f(x) вздовж вісі ОХ на -k одиниць Y=f(x)+k Паралельне перенесення графіка функції y=f(x) вздовж вісі ОУ на k одиниць Y=kf(x) Розтяг графіка функції y=f(x) вздовж вісі ОУ у k разів Y=f(kx) Стиск графіка функції y=f(x) вздовж вісі ОХ у k разів Y=f(│x│) Симетрія частини графіка функції y=f(x), де х≥ 0 відносно вісі ОУ Y=│f(x)│ Симетрія від’ємної частини графіка функції y=f(x) відносно вісі ОХ Y=f(x/k) Розтяг графіка функції y=f(x) вздовж вісі ОX у k разів Y=1/k f(x) Стиск графіка функції y=f(x) вздовж вісі ОY у k разів

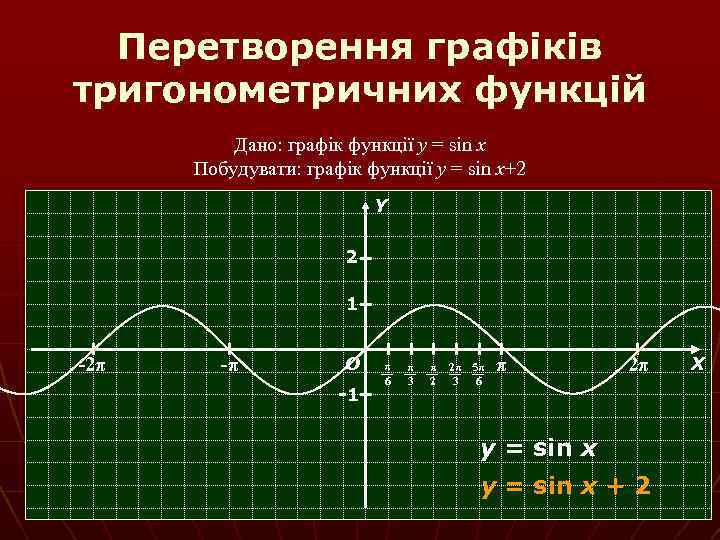Перетворення графіків тригонометричних функцій Дано: графік функції y = sin x Побудувати: графік функції y = sin x+2 Y 2 1 -2π -π О -1 π 6 π 3 π 2 2π 5π 3 6 π 2π y = sin x + 2 Х

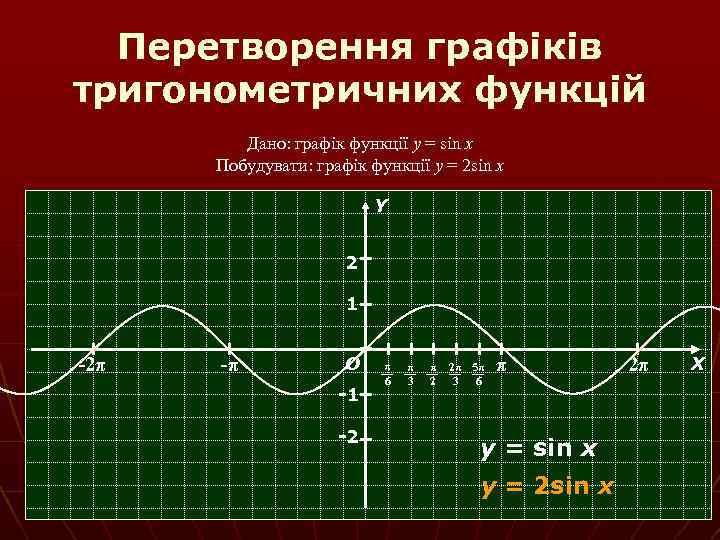Перетворення графіків тригонометричних функцій Дано: графік функції y = sin x Побудувати: графік функції y = 2 sin x Y 2 1 -2π -π О -1 -2 π 6 π 3 π 2 2π 5π 3 6 π y = sin x y = 2 sin x 2π Х

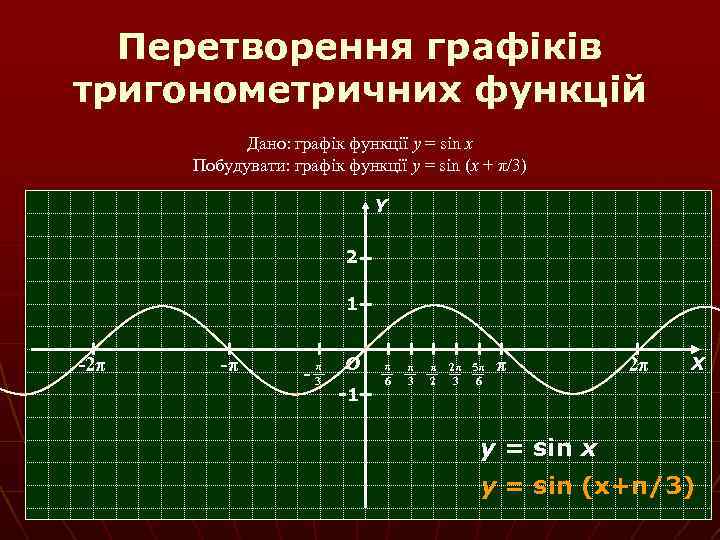Перетворення графіків тригонометричних функцій Дано: графік функції y = sin x Побудувати: графік функції y = sin (x + π/3) Y 2 1 -2π -π π -3 О -1 π 6 π 3 π 2 2π 5π 3 6 π 2π Х y = sin x y = sin (x+π/3)

Перетворення графіків тригонометричних функцій Дано: графік функції y = sin x Побудувати: графік функці] y = sin 2 x Y 1 -2π -π О -1 π 6 π 3 π 2 2π 5π 3 6 π y = sin x y = sin 2 x 2π Х

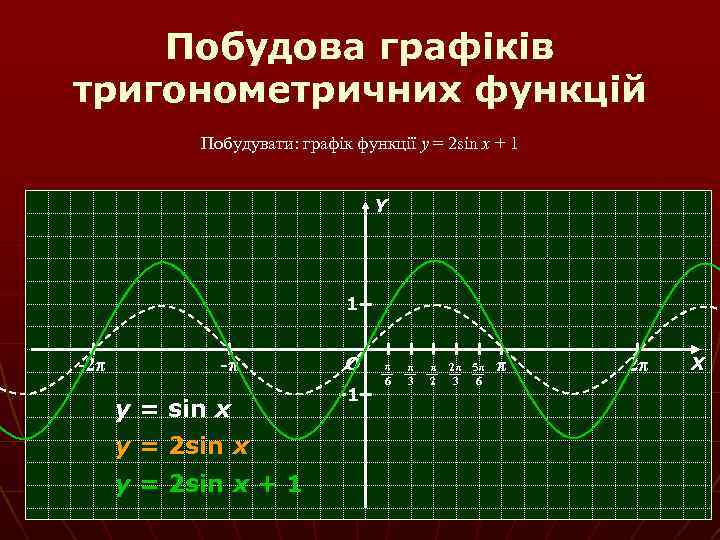Побудова графіків тригонометричних функцій Побудувати: графік функції y = 2 sin x + 1 Y 1 -2π -π y = sin x y = 2 sin x + 1 О -1 π 6 π 3 π 2 2π 5π 3 6 π 2π Х

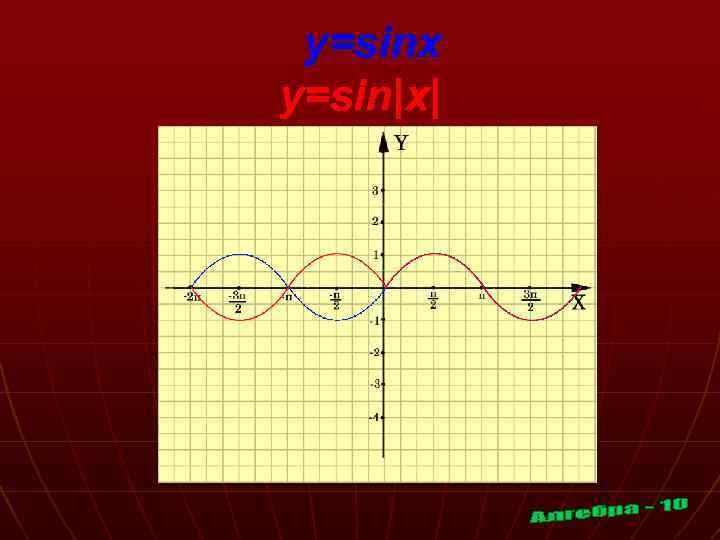y=sinx y=sin|x|

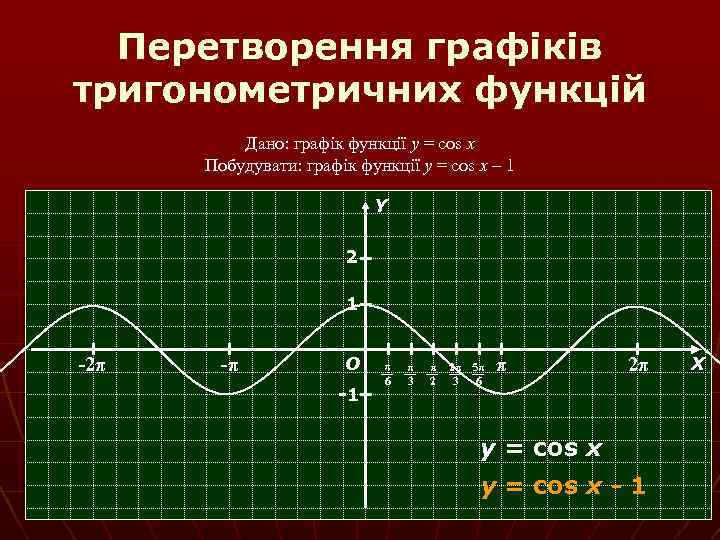Перетворення графіків тригонометричних функцій Дано: графік функції y = cos x Побудувати: графік функції y = cos x – 1 Y 2 1 -2π -π О -1 π 6 π 3 π 2 2π 5π 3 6 π 2π y = cos x - 1 Х

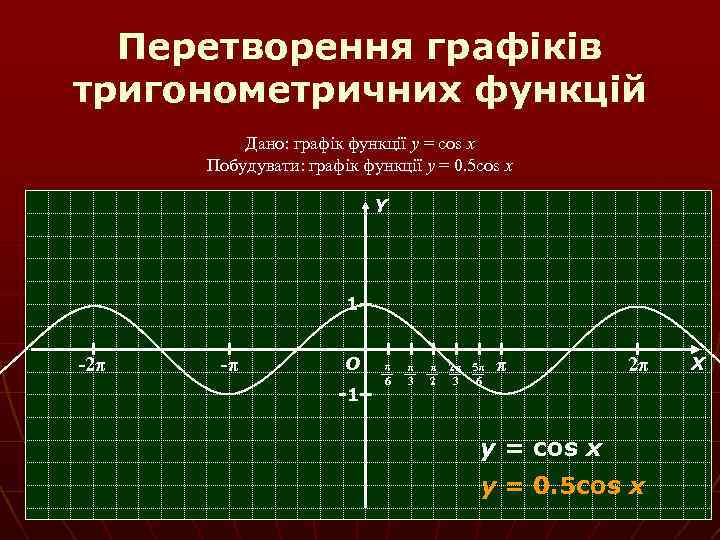Перетворення графіків тригонометричних функцій Дано: графік функції y = cos x Побудувати: графік функції y = 0. 5 cos x Y 1 -2π -π О -1 π 6 π 3 π 2 2π 5π 3 6 π 2π y = cos x y = 0. 5 cos x Х

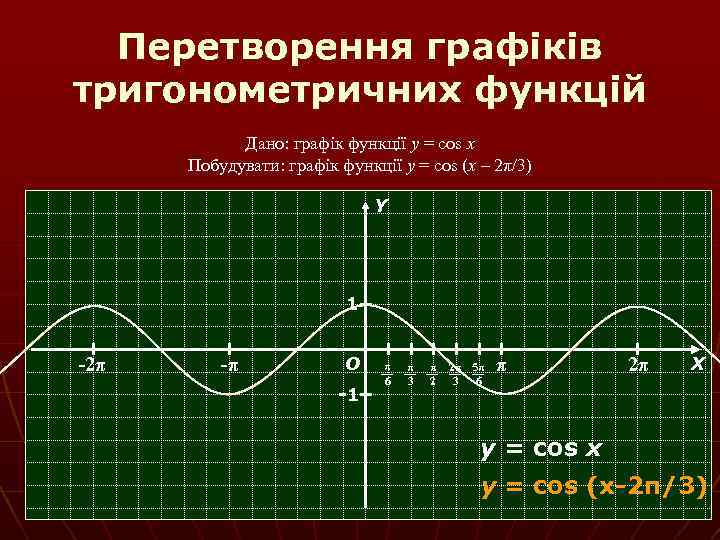Перетворення графіків тригонометричних функцій Дано: графік функції y = cos x Побудувати: графік функції y = cos (x – 2π/3) Y 1 -2π -π О -1 π 6 π 3 π 2 2π 5π 3 6 π 2π Х y = cos x y = cos (x-2π/3)

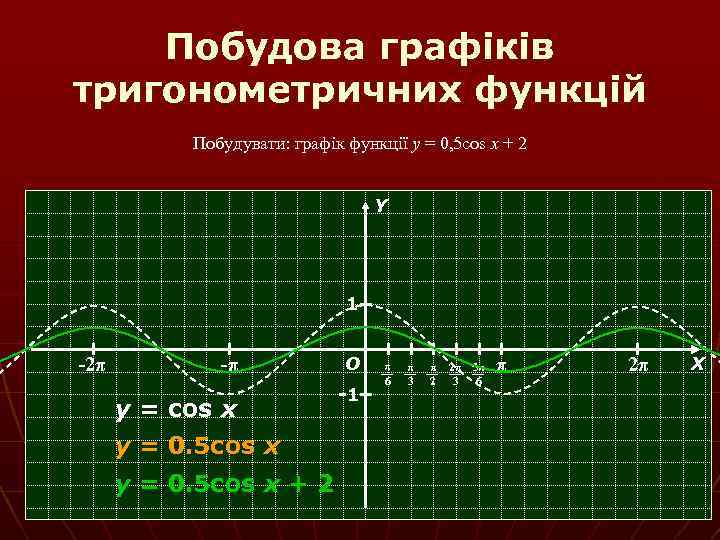Побудова графіків тригонометричних функцій Побудувати: графік функції y = 0, 5 cos x + 2 Y 1 -2π -π y = cos x y = 0. 5 cos x + 2 О -1 π 6 π 3 π 2 2π 5π 3 6 π 2π Х

y=cosx y=cos 2 x y=cos(1/2 x)

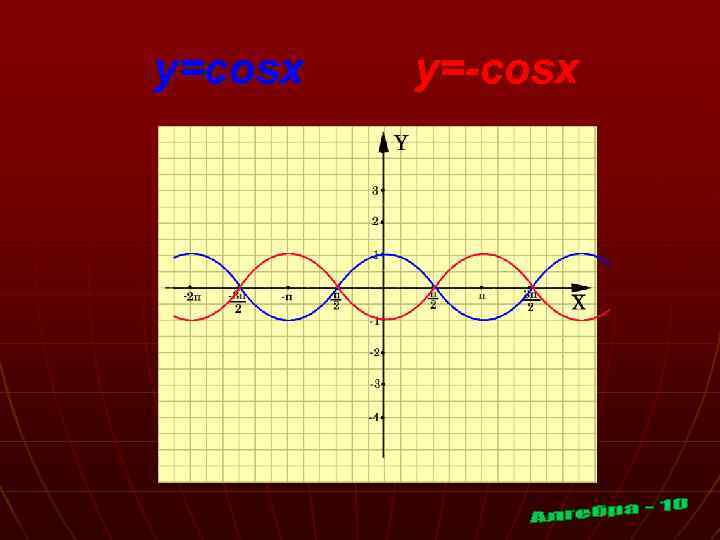y=cosx y=-cosx

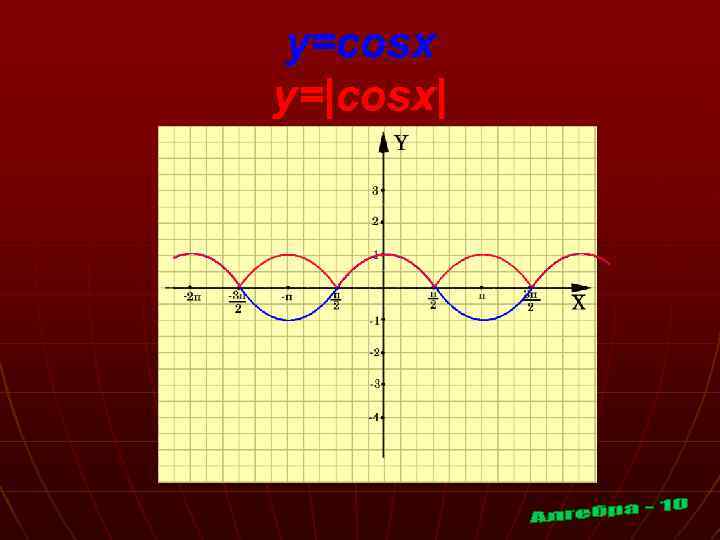y=cosx y=|cosx|

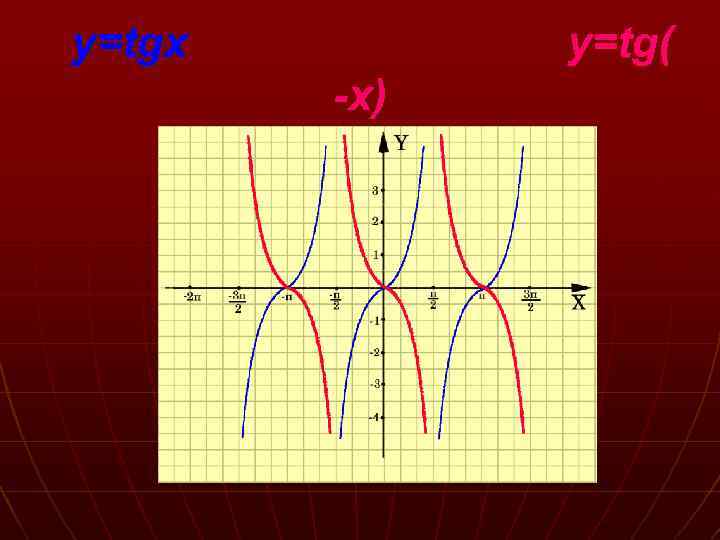y=tgx y=tg( -x)

Побудова графіків тригонометричних функцій Побудуйте графіки функцій: y = 2 cos x + 1 y = 2 cos (x+π/6) + 1 y = 2 sin (x – π/3) – 1 y = 2 sin 2 x + 1 y = 0. 5 cos 2 x + 1

Домашнє завдання 1. Знайти періоди функцій: y = cos 4 x; y = sin (6 – 2 x); y = ctg (x – π) 2. Побудувати графіки функцій: y = 2 sin (x+π/3)+3; y = 0. 5 cos x – 1 3. Повторити значення синусів, косинусів, тангенсів від 0 до 1800