Пересечение многогранных поверхностей Две многогранные поверхности в

Пересечение многогранных поверхностей

Две многогранные поверхности в общем случае пересекаются по пространственной замкнутой ломаной линии Проницание частичное

В частных случаях эта ломаная может распадаться на две и более замкнутые ломаные линии, на плоскую и пространственную линии Проницание частичное Две замкнутые ломаные линии (плоская и пространственная) Проницание полное Две замкнутые ломаные линии ( обе плоские)

Способ ребер построение вершин ломаной как точек пересечения ребер первого многогранника с гранями второго и ребер второго с гранями первого прямыми соединяются проекции только тех точек, которые принадлежат одной грани Способ граней построение сторон ломаной как отрезков прямых попарного пересечения граней данных многогранников

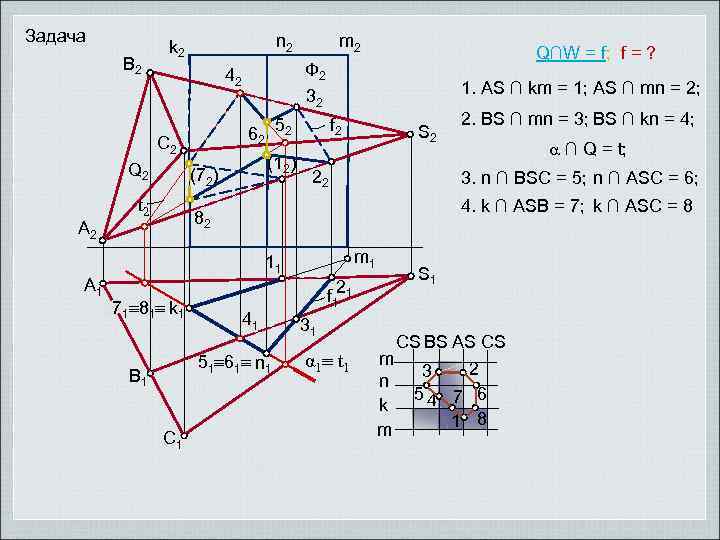Задача B 2 n 2 k 2 А 1 (12) (72) t 2 1. AS ∩ km = 1; AS ∩ mn = 2; f 2 62 52 C 2 Q∩W = f; f = ? Ф 2 32 42 Q 2 m 2 S 2 22 4. k ∩ ASB = 7; k ∩ ASC = 8 m 1 11 41 51 61 n 1 В 1 С 1 ∩ Q = t; 3. n ∩ BSC = 5; n ∩ ASC = 6; 82 71 81 k 1 2. BS ∩ mn = 3; BS ∩ kn = 4; S 1 2 f 1 1 31 α 1 t 1 m n k m CS BS AS CS 2 3 54 7 6 1 8