ПЕРЕСЕЧЕНИЕ МНОГОГРАННИКА ПРЯМОЙ Задачи на определение точек пересечения

ПЕРЕСЕЧЕНИЕ МНОГОГРАННИКА ПРЯМОЙ Задачи на определение точек пересечения прямой линии с многогранником решают в соответствии с алгоритмом решения задач на пересечение прямой с плоскостью.

Алгоритм решения: 1) заключаем заданную прямую (АВ) в проецирующую плоскость (α ┴ П 2); 2) находим линию пересечения вспомогательной плоскости с поверхностью; 3) определяем точки пересечения линии сечения (123) с заданной прямой (АВ); Эти точки (М и N) и будут искомыми точками пересечения прямой с поверхностью.

Кривые поверхности широко применяются в различных областях науки и техники при создании очертаний различных технических форм. Способы задания кривых поверхностей: 1. Аналитический - при помощи уравнений; 2. При помощи каркаса; 3. Кинематический, т. е. перемещением линий в пространстве.

2. Каркас поверхности. Каркасом поверхности принято называть упорядоченное множество точек или линий, принадлежащих поверхности. Линейным каркасом называется множество линий, имеющих единый закон образования и связанных между собой определенной зависимостью. Пример каркаса поверхности, состоящей из двух ортогонально расположенных семейств линий а 1, а 2, а 3, …, аn, b 1, b 2, b 3, …bn.

3. Кинематический, т. е. перемещением линий в пространстве. Поверхность можно рассматривать, как совокупность последовательных положений l 1, l 2… линии l, перемещающейся в пространстве по определенному закону. В процессе образования поверхности линия l может оставаться неизменной или менять свою форму - изгибаться или деформироваться. Подвижную линию принято называть образующей, неподвижные направляющими.

По закону движения образующих можем иметь поверхности - с поступательным движением, - с вращательным движением поверхности вращения, - с винтовым движением - винтовые поверхности. По признаку развертывания поверхности могут быть развертываемыми и неразвертываемыми. По признаку направляющих, которые могут быть ломаными, прямыми или кривыми, поверхности могут быть гранными или кривыми.

По форме образующей поверхности делятся на линейчатые, когда образующая - прямая и нелинейчатые , когда образующая - кривая.

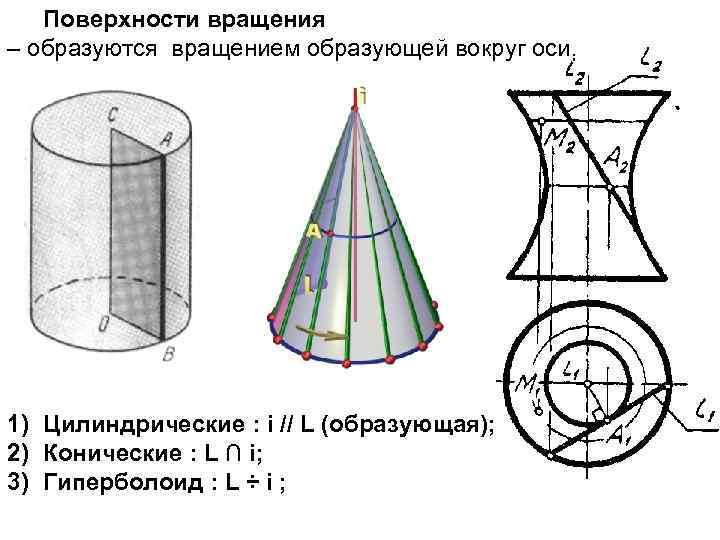Поверхности вращения – образуются вращением образующей вокруг оси. 1) Цилиндрические : i // L (образующая); 2) Конические : L ∩ i; 3) Гиперболоид : L ÷ i ;

Особое место среди поверхностей вращения занимают сферические поверхности - шар, открытый тор (кольцо), закрытый тор, а так же эллипсоид вращения, гиперболоид вращения, параболоид вращения. Эти поверхности называются алгебраическими поверхностями, т. к. их можно задавать формулой. Поверхности вращения задаются проекциями – очерками.

Параболоид вращения Эллипсоид вращения

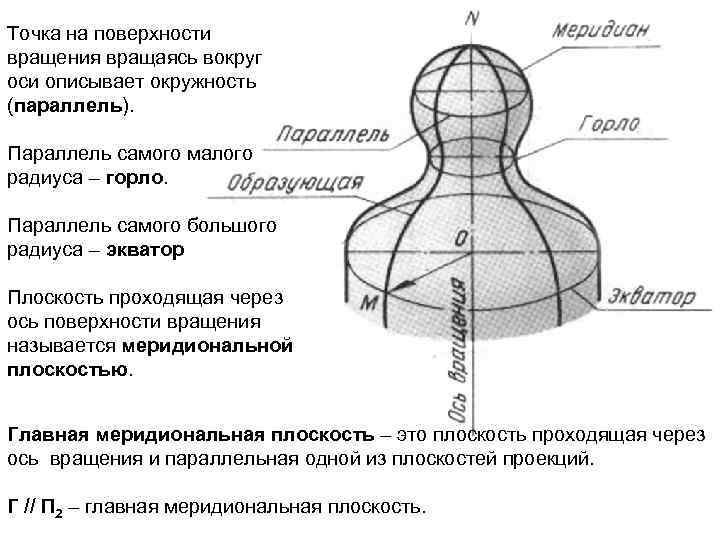Точка на поверхности вращения вращаясь вокруг оси описывает окружность (параллель). Параллель самого малого радиуса – горло. Параллель самого большого радиуса – экватор Плоскость проходящая через ось поверхности вращения называется меридиональной плоскостью. Главная меридиональная плоскость – это плоскость проходящая через ось вращения и параллельная одной из плоскостей проекций. Г // П 2 – главная меридиональная плоскость.

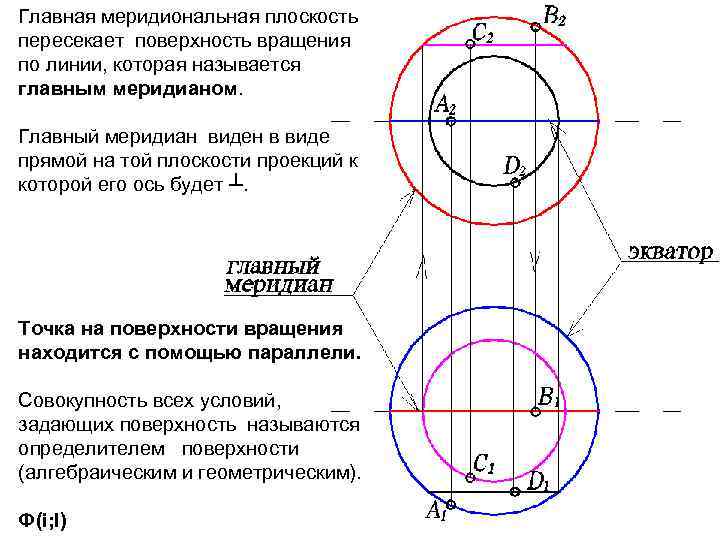Главная меридиональная плоскость пересекает поверхность вращения по линии, которая называется главным меридианом. Главный меридиан виден в виде прямой на той плоскости проекций к которой его ось будет ┴. Точка на поверхности вращения находится с помощью параллели. Совокупность всех условий, задающих поверхность называются определителем поверхности (алгебраическим и геометрическим). Ф(i; l)

Поверхность считается заданной, если однозначно решен вопрос о принадлежности (. ) этой поверхности. Все точки, расположенные над экватором, на горизонтальной плоскости проекций видимы (под экватором – невидимы). Все (. ), расположенные перед гл. меридианом, на фронтальной плоскости проекций видимы ( за гл. меридианом – невидимы).

Точки на поверхности вращения можно построить с помощью образующих.

ПЕРЕСЕЧЕНИЕ ПОВЕРХНОСТИ ПЛОСКОСТЬЮ

Коническая поверхность. При пересечении конической поверхности проецирующей плоскостью сечение проецируется как: α - проходит через вершину конуса - треугольник α ┴ i – окружность α ∩ все образующие – эллипс α // одной образующей – парабола α // i – гипербола

Цилиндрическая поверхность. При пересечении цилиндрической поверхности проецирующей плоскостью сечение проецируется как: - эллипс, окружность, прямоугольник, парабола.

Сфера При пересечении сферы проецирующей плоскостью сечение проецируется на плоскости проекций как: окружность, прямая, эллипс.

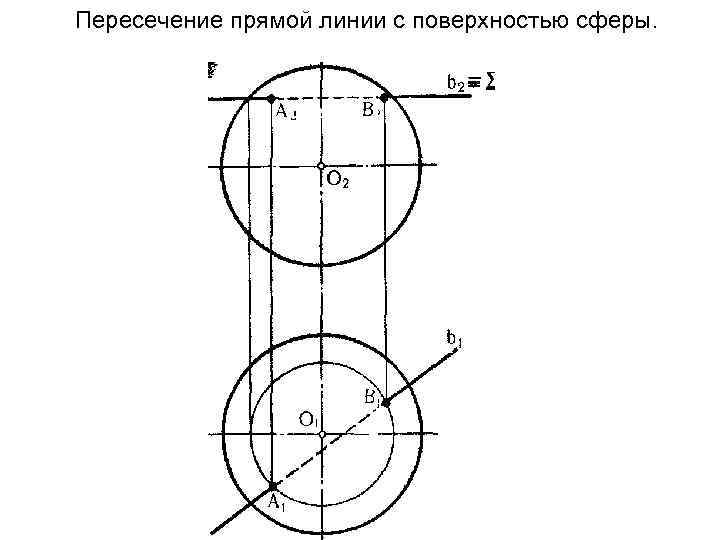Пересечение прямой линии с поверхностью сферы.

Пересечение прямой линии с поверхностью конуса.

Пересечение прямой линии с поверхностью сферы. Данную задачу целесообразно решать, применяя способ замены плоскостей проекций.

Взаимное пересечение поверхностей