Пересечение кривых поверхностей_53_в.pptx
- Количество слайдов: 22
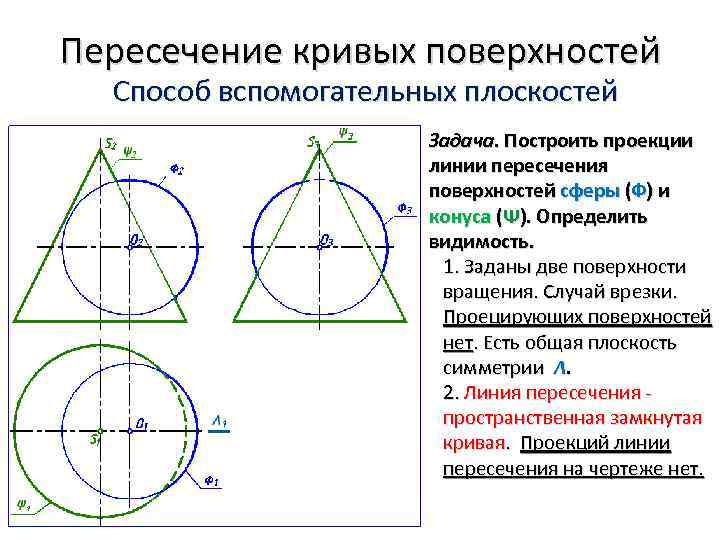
Пересечение кривых поверхностей Способ вспомогательных плоскостей Задача. Построить проекции линии пересечения поверхностей сферы (Ф) и конуса (Ψ). Определить видимость. 1. Заданы две поверхности вращения. Случай врезки. Проецирующих поверхностей нет. Есть общая плоскость симметрии Λ. 2. Линия пересечения пространственная замкнутая кривая. Проекций линии пересечения на чертеже нет.
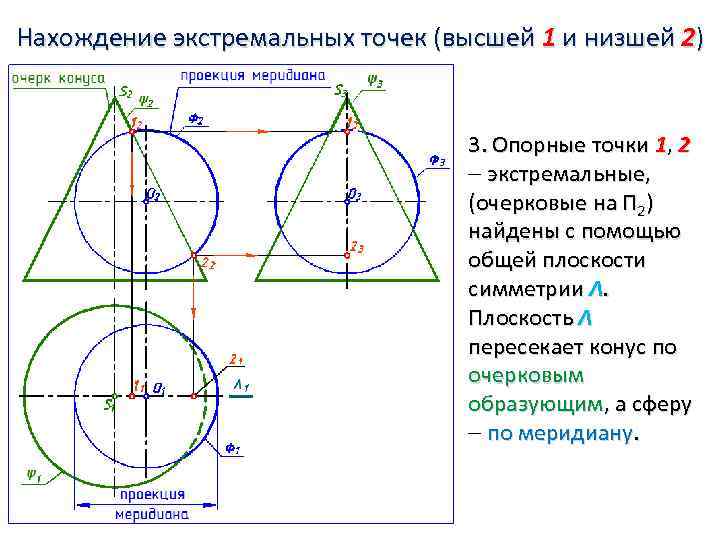
Нахождение экстремальных точек (высшей 1 и низшей 2) 3. Опорные точки 1, 2 экстремальные, (очерковые на П 2) найдены с помощью общей плоскости симметрии Λ. Плоскость Λ пересекает конус по очерковым образующим, а сферу по меридиану.
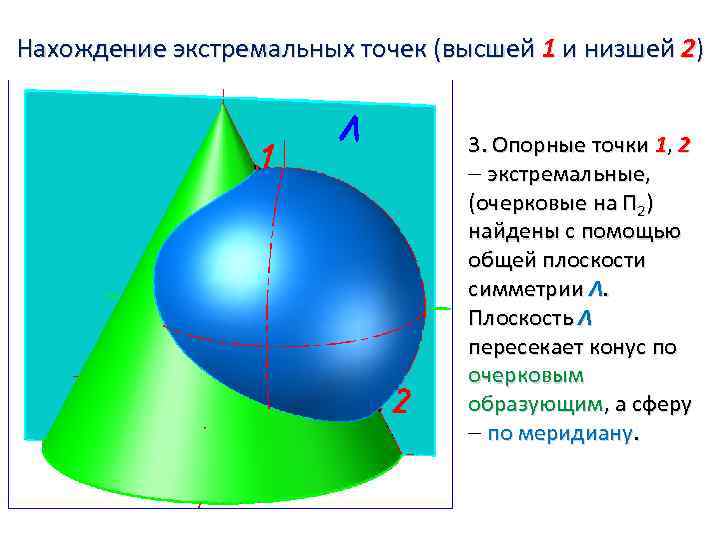
Нахождение экстремальных точек (высшей 1 и низшей 2) 3. Опорные точки 1, 2 экстремальные, (очерковые на П 2) найдены с помощью общей плоскости симметрии Λ. Плоскость Λ пересекает конус по очерковым образующим, а сферу по меридиану.
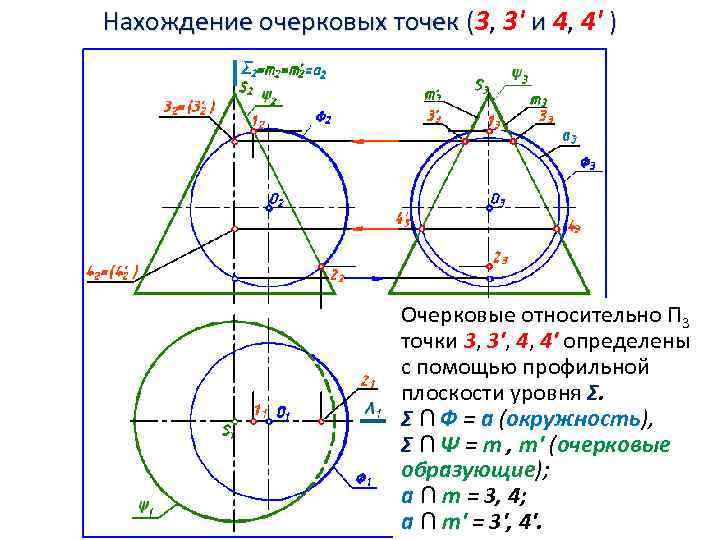
Нахождение очерковых точек (3, 3' и 4, 4' ) Очерковые относительно П 3 точки 3, 3', 4, 4' определены с помощью профильной плоскости уровня Σ. Σ ∩ Ф = а (окружность), Σ ∩ Ψ = m , m' (очерковые образующие); a ∩ m = 3, 4; a ∩ m' = 3', 4'.

Нахождение очерковых точек (3, 3' и 4, 4' ) Очерковые относительно П 3 точки 3, 3', 4, 4' определены с помощью профильной плоскости уровня Σ. Σ∩Ф=а (окружность), Σ ∩ Ψ = m , m' (очерковые образующие); a ∩ m = 3, 4; a ∩ m' = 3', 4'.
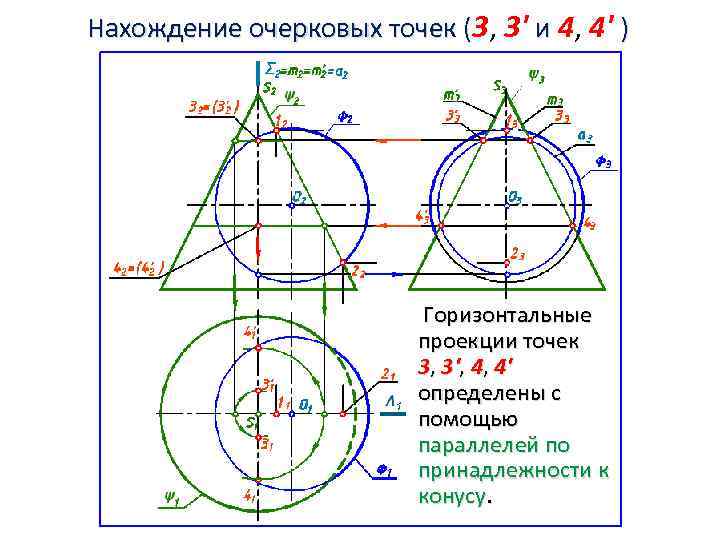
Нахождение очерковых точек (3, 3' и 4, 4' ) Горизонтальные проекции точек 3, 3', 4, 4' определены с помощью параллелей по принадлежности к конусу.
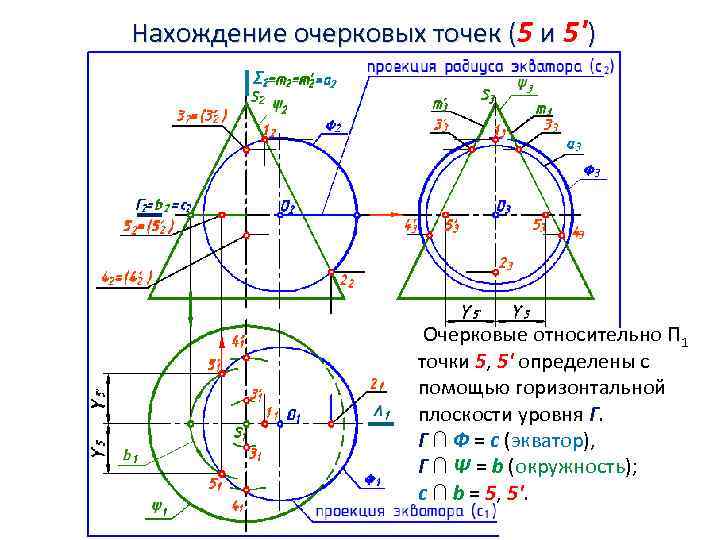
Нахождение очерковых точек (5 и 5') Очерковые относительно П 1 точки 5, 5' определены с помощью горизонтальной плоскости уровня Г. Г ∩ Ф = с (экватор), Г ∩ Ψ = b (окружность); c ∩ b = 5, 5'.

Нахождение очерковых точек (5 и 5') Ψ Ф Очерковые относительно П 1 точки 5, 5' определены с помощью горизонтальной плоскости уровня Г. Г ∩ Ф = с (экватор), Г∩Ψ=b (окружность); c ∩ b = 5, 5'.
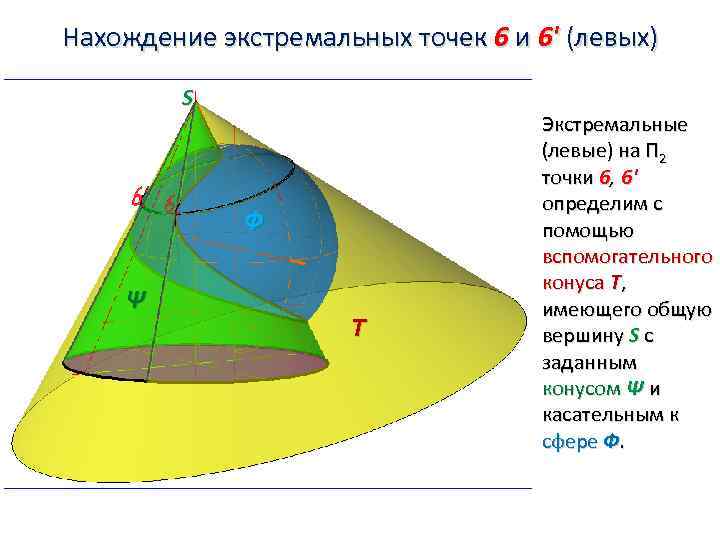
Нахождение экстремальных точек 6 и 6' (левых) S Φ Ψ T Экстремальные (левые) на П 2 точки 6, 6' определим с помощью вспомогательного конуса Т, имеющего общую вершину S с заданным конусом Ψ и касательным к сфере Ф.
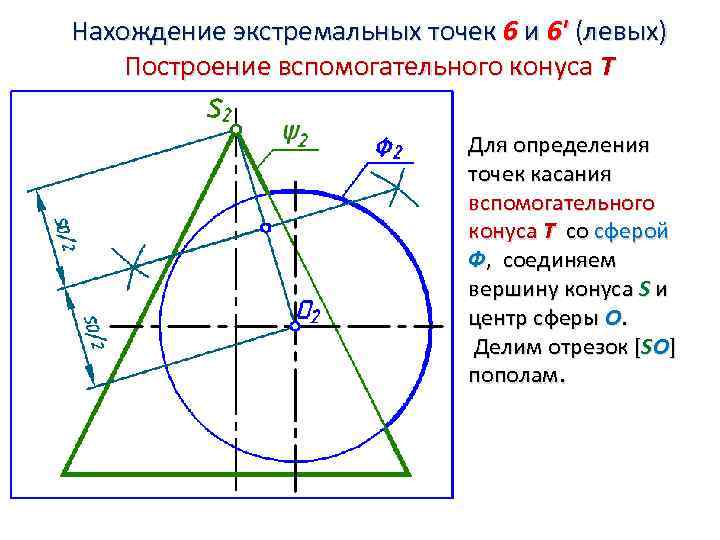
Нахождение экстремальных точек 6 и 6' (левых) Построение вспомогательного конуса Т Для определения точек касания вспомогательного конуса Т со сферой Ф, соединяем вершину конуса S и центр сферы О. Делим отрезок [SО] пополам.
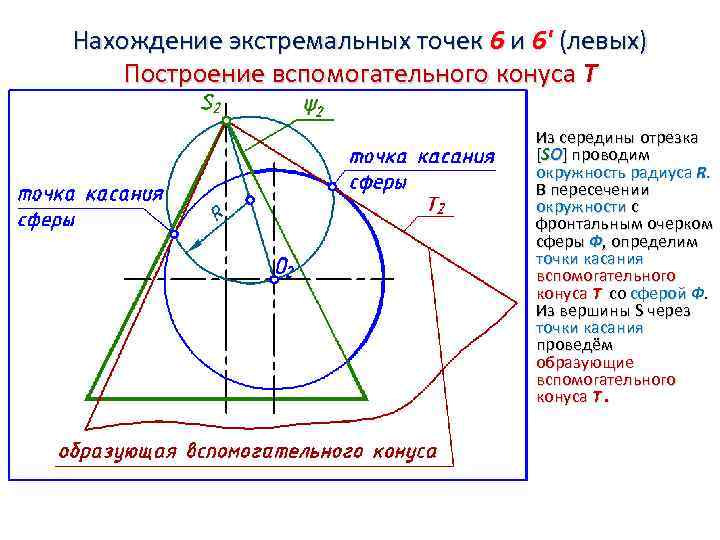
Нахождение экстремальных точек 6 и 6' (левых) Построение вспомогательного конуса Т Из середины отрезка [SО] проводим окружность радиуса R. В пересечении окружности с фронтальным очерком сферы Ф, определим точки касания вспомогательного конуса Т со сферой Ф. Из вершины S через точки касания проведём образующие вспомогательного конуса Т.
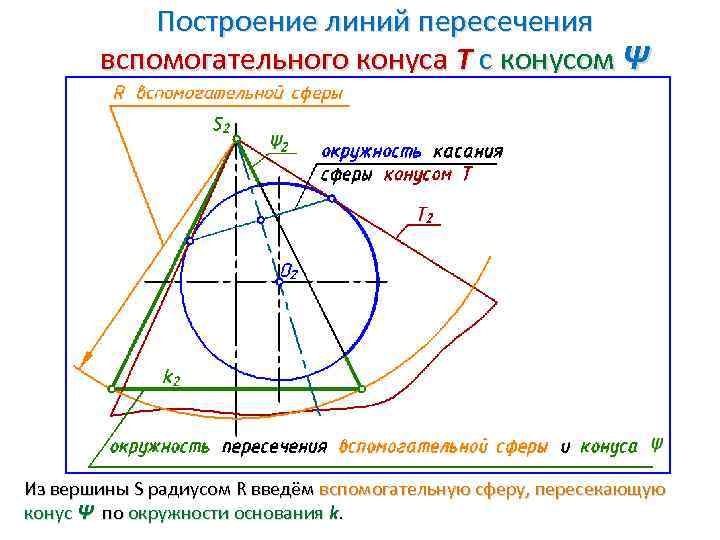
Построение линий пересечения вспомогательного конуса Т с конусом Ψ Из вершины S радиусом R введём вспомогательную сферу, пересекающую конус Ψ по окружности основания k.
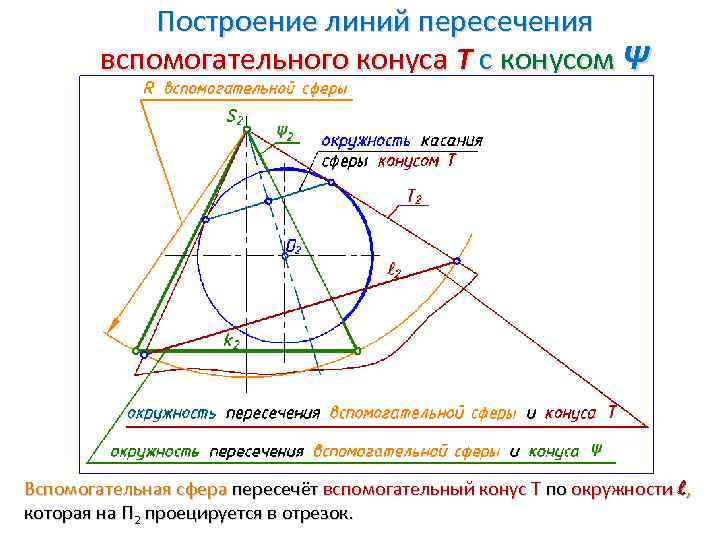
Построение линий пересечения вспомогательного конуса Т с конусом Ψ Вспомогательная сфера пересечёт вспомогательный конус Т по окружности l, которая на П 2 проецируется в отрезок.
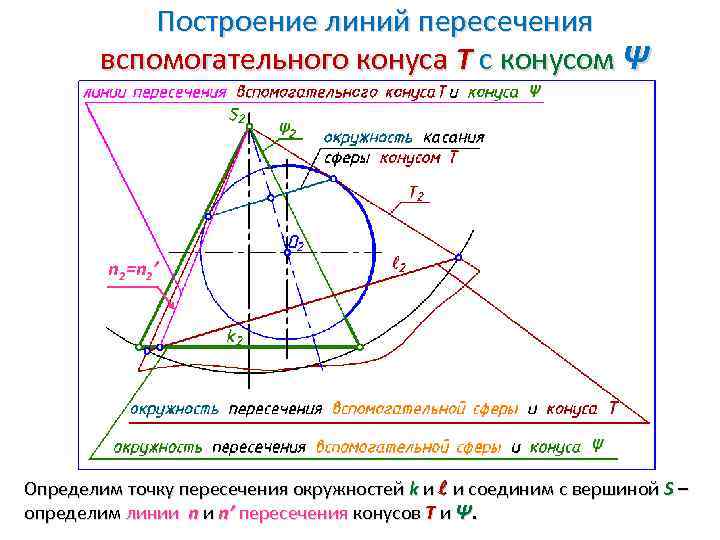
Построение линий пересечения вспомогательного конуса Т с конусом Ψ n 2=n 2’ Определим точку пересечения окружностей k и l и соединим с вершиной S – определим линии n и n’ пересечения конусов Т и Ψ.
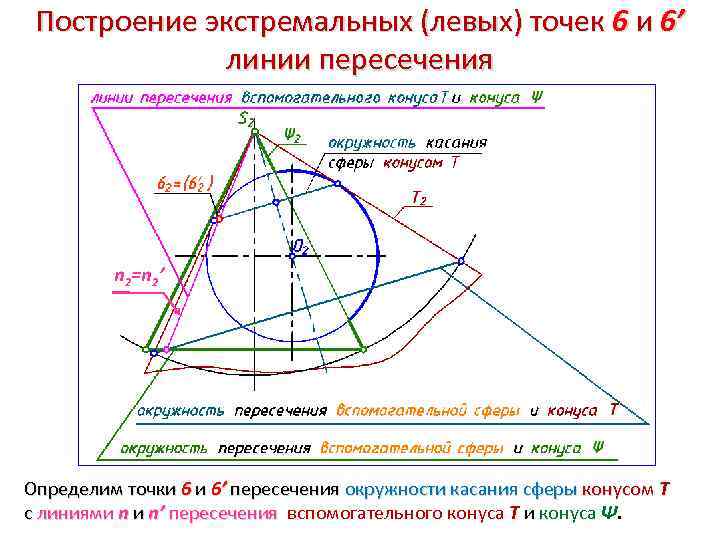
Построение экстремальных (левых) точек 6 и 6’ линии пересечения n 2=n 2’ Определим точки 6 и 6’ пересечения окружности касания сферы конусом Т с линиями n и n’ пересечения вспомогательного конуса Т и конуса Ψ.
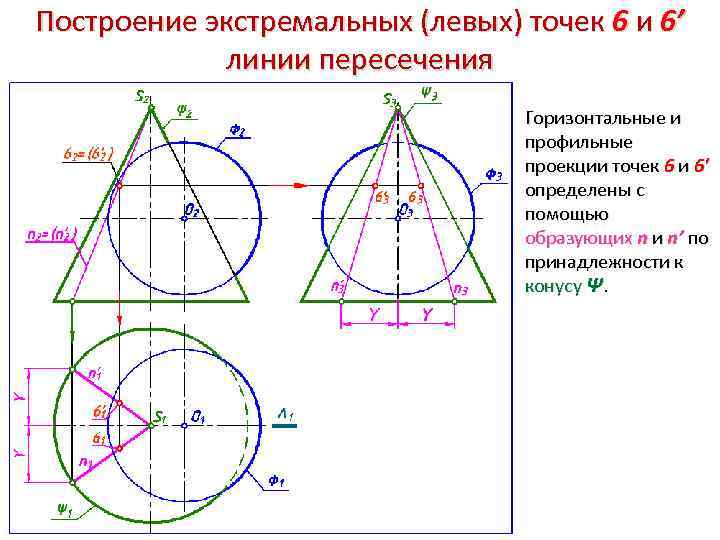
Построение экстремальных (левых) точек 6 и 6’ линии пересечения Горизонтальные и профильные проекции точек 6 и 6' определены с помощью образующих n и n’ по принадлежности к конусу Ψ.
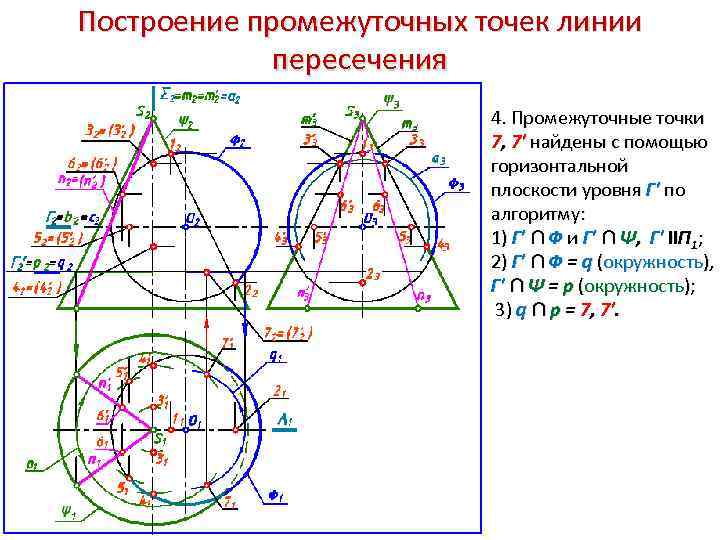
Построение промежуточных точек линии пересечения 4. Промежуточные точки 7, 7' найдены с помощью горизонтальной плоскости уровня Г' по алгоритму: 1) Г' ∩ Ф и Г' ∩ Ψ, Г' IIП 1; 2) Г' ∩ Ф = q (окружность), Г' ∩ Ψ = p (окружность); 3) q ∩ p = 7, 7'.
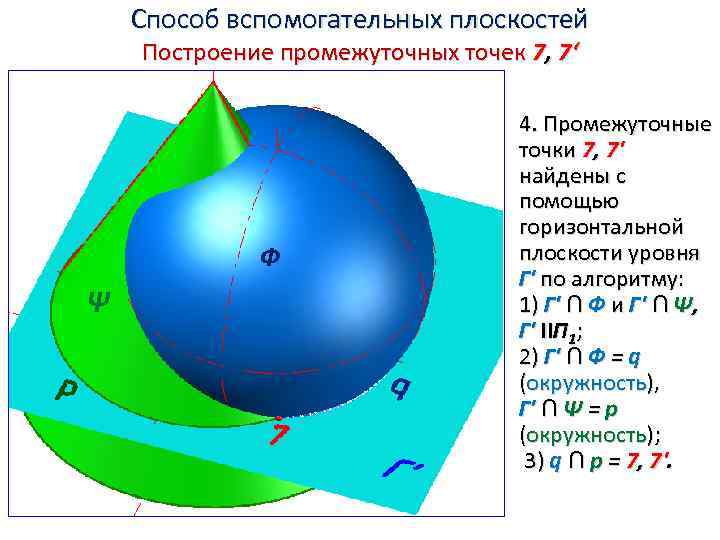
Способ вспомогательных плоскостей Построение промежуточных точек 7, 7‘ Ф Ψ 4. Промежуточные точки 7, 7' найдены с помощью горизонтальной плоскости уровня Г' по алгоритму: 1) Г' ∩ Ф и Г' ∩ Ψ, Г' IIП 1; 2) Г' ∩ Ф = q (окружность), Г' ∩ Ψ = p (окружность); 3) q ∩ p = 7, 7'.
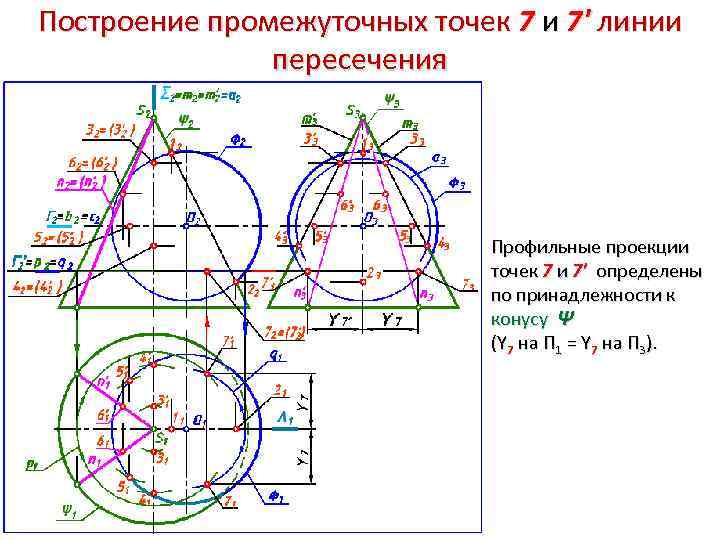
Построение промежуточных точек 7 и 7' линии пересечения Профильные проекции точек 7 и 7' определены по принадлежности к конусу Ψ (Y 7 на П 1 = Y 7 на П 3).
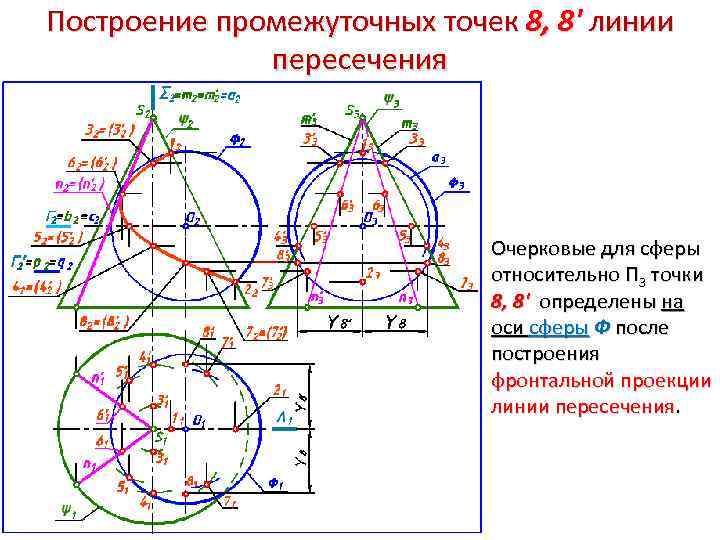
Построение промежуточных точек 8, 8' линии пересечения Очерковые для сферы относительно П 3 точки 8, 8' определены на оси сферы Ф после построения фронтальной проекции линии пересечения.
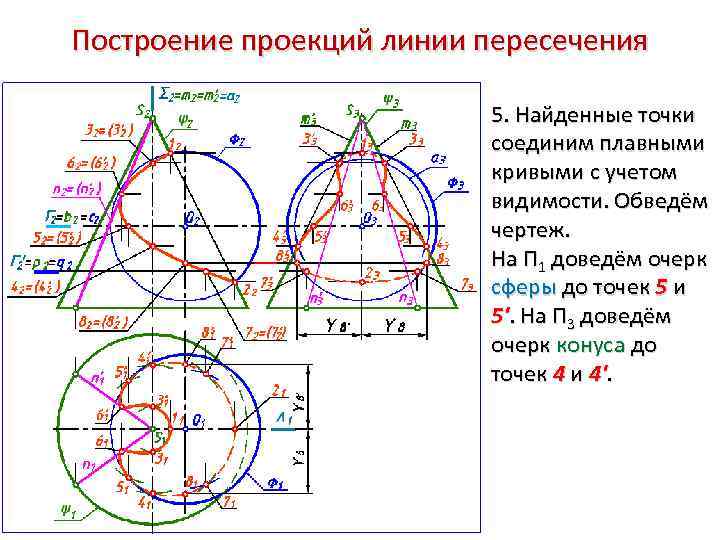
Построение проекций линии пересечения 5. Найденные точки соединим плавными кривыми с учетом видимости. Обведём чертеж. На П 1 доведём очерк сферы до точек 5 и 5'. На П 3 доведём очерк конуса до точек 4 и 4'.
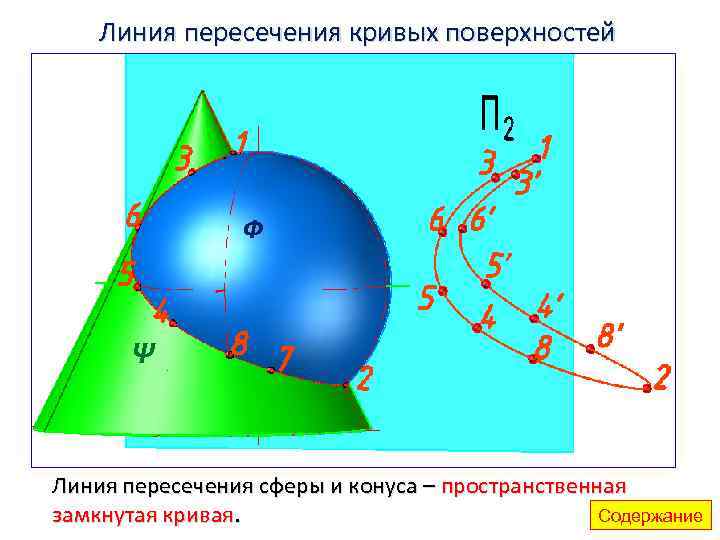
Линия пересечения кривых поверхностей Ф Ψ Линия пересечения сферы и конуса – пространственная Содержание замкнутая кривая.
Пересечение кривых поверхностей_53_в.pptx