Переменный синусоидальный ток Лекция 3 Способы представления

Переменный синусоидальный ток Лекция 3

Способы представления синусоидальных токов, напряжений, ЭДС 1. Аналитический способ Для тока i(t) = Im sin(ωt + ψi) для напряжения u(t) = Um sin (ωt +ψu) для ЭДС e(t) = Em sin (ωt +ψe) Im, Um, Em – амплитуды тока, напряжения, ЭДС; значение в скобках – фаза; ψi, ψu, ψe – начальная фаза тока, напряжения, ЭДС; ω – циклическая частота [рад/с], ω = 2πf; f – частота, f = 1 / T; Т – период. Значения начальных фаз ψi, ψu, ψe могут измеряться в радианах или градусах. Величина ψi, ψu, ψe зависит от начала отсчета времени t = 0. Положительное значение откладывается влево, отрицательное – вправо.

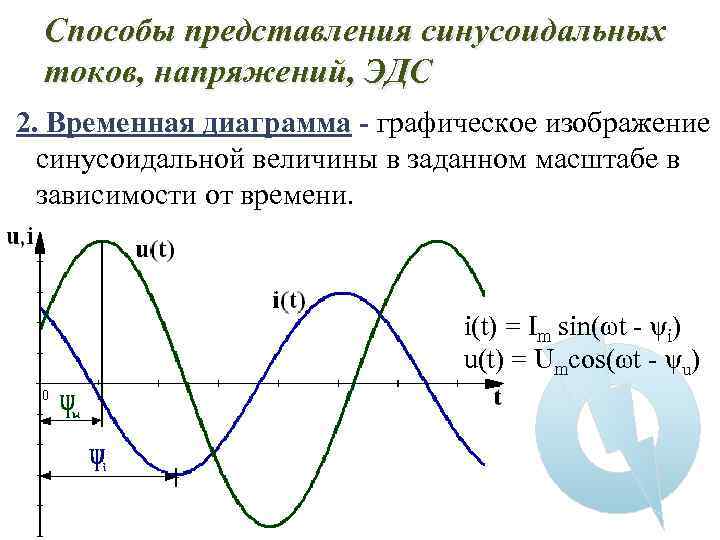
Способы представления синусоидальных токов, напряжений, ЭДС 2. Временная диаграмма - графическое изображение синусоидальной величины в заданном масштабе в зависимости от времени. i(t) = Im sin(ωt - ψi) u(t) = Umcos(ωt - ψu)

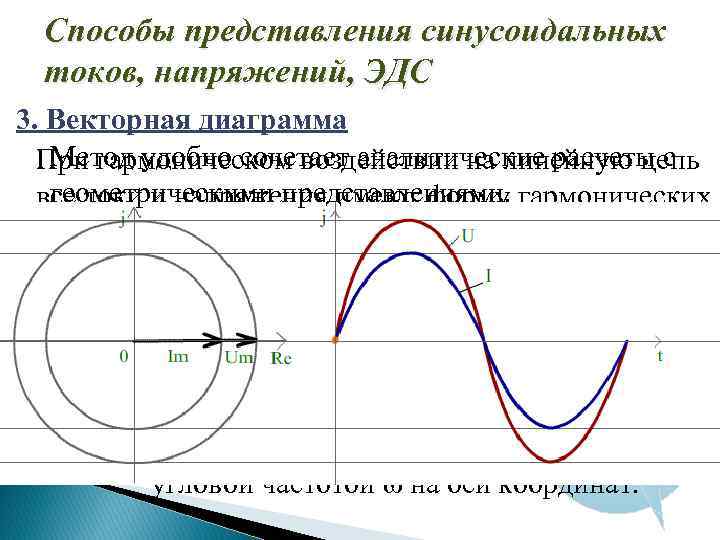
Способы представления синусоидальных токов, напряжений, ЭДС 3. Векторная диаграмма Метод удобно сочетает аналитические расчеты с При гармоническом воздействии на линейную цепь геометрическими представлениями. все токи и напряжения имеют форму гармонических колебаний, поэтому задача расчета цепи сводится к нахождению амплитуд и начальных фаз этих колебаний. В связи с этим был разработан метод комплексных амплитуд. Гармонические колебания согласно этому методу могут быть представлены как проекции вектора Um на комплексной плоскости вращающегося против часовой стрелки с угловой частотой ω на оси координат.

Топографическая диаграмма. Алгоритм. 1. Топографическая диаграмма представляет собой векторную диаграмму, на которой отложены 4. Вектора должны следовать друг за другом. комплексные потенциалы отдельных точек заданной 5. Обход схемы следует вести согласно выбранному цепи по отношению к одной точке, потенциал которой условному положительному направлению. принят за ноль. 6. Вектор напряжения на диаграмме направлен к точке высшего(уменьшающегося) потенциала, а тоже 2. Порядок расположения векторов падений напряжение на схеме указывается стрелкой, должен строго соответствовать порядку расположения направленной от высшего к низшему потенциалу. на схеме. 7. Вектора ЭДС направлены одинаково с положительным 3. Первым откладывается вектор, являющийся общим для направлением ЭДС относительно соответствующих всех элементов цепи. точек схемы.

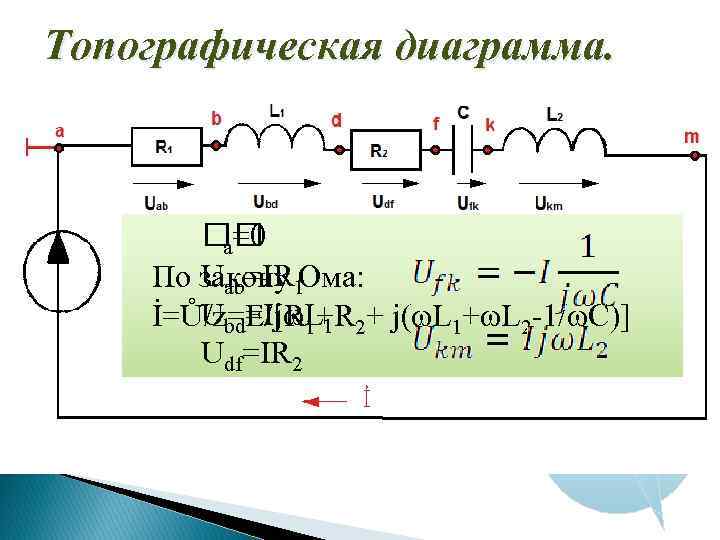
Топографическая диаграмма. a=0 Uab=IR 1 По закону Ома: Ubd=IjωL 1 İ=Ů/z=E/[R 1+R 2+ j(ωL 1+ωL 2 -1/ωC)] Udf=IR 2

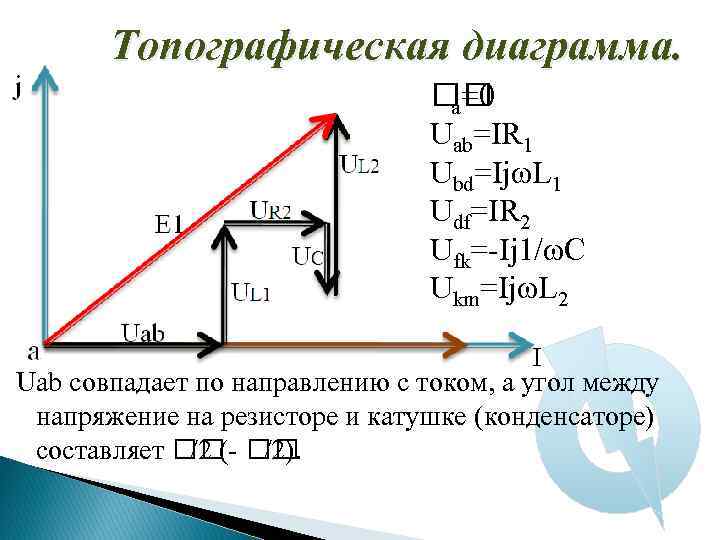
Топографическая диаграмма. a=0 Uab=IR 1 Ubd=IjωL 1 Udf=IR 2 Ufk=-Ij 1/ωC Ukm=IjωL 2 Uab совпадает по направлению с током, а угол между напряжение на резисторе и катушке (конденсаторе) составляет /2). /2 (-

Среднее и действующее значение синусоидальных тока, напряжения и ЭДС Принято среднее значение определять за период Действующим значением синусоидальной функции называется ее среднеквадратичное значение за период Для синусоидальной функции среднее значение за период равно нулю. Используется также понятие среднего значения синусоидальной функции за полпериода: Аналогично, определяется среднее значение ЭДС и напряжения за полпериода

Большинство измерительных приборов амперметров и вольтметров показывают действующее значение измеряемой величины. Переменный ток, в отличие от тока постоянного, непрерывно изменяется как по величине, так и по направлению, причем изменения эти происходят периодически, т. е. точно повторяются через равные промежутки времени. Поэтому законы для постоянного тока справедливы и для переменного, только берутся комплексные значения. Через конденсатор постоянный ток не протекает => в цепях постоянного тока рассматривать C и L бессмысленно.

Закон Ома для комплексных амплитуд İ=Ů/z y=g±ib z= r ± ix комплексная проводимость; комплексное сопротивление; b= b - bc| x= |xl l– xc реактивная составляющая компл. проводимости реактивное сопротивление; xl=iωL bl=1/xl =1/iωL реактивное сопротивление индуктивности; x=1/x = -iωC bc c= -1/iωC c реактивное сопротивление ёмкости;

Переменный ток в резисторе В резисторе протекает синусоидальный ток: i(t) = Im. R sin(ωt + ψi). Воспользуемся законом Ома для мгновенных значений u(t) = R i(t) => u(t) = RIm. R sin(ωt + ψi) Формальная запись синусоидального напряжения имеет вид: u(t) = Um. R sin(ωt + ψu) Соотношения равны, если выполнены условия равенства u(t) = Um. R sin(ωt + ψ = ψ амплитуд и фаз Um. R = RIm. R , ψu u) i. для действующих значений : UR = RIR. Фазы напряжения и тока в резисторе совпадают

Переменный ток в индуктивности Через катушку протекает переменный ток: Im i(t) = Im. R sin(ωt + ψi) Полученный результат показывает, что напряжение на Напряжение на зажимах катушки (ЭДС самоиндукции): . катушке индуктивности опережает по фазе ток на /2 UL el=-L(di/dt) IL Таким образом, если на входы двухлучевого осциллографа Векторная диаграмма Дифференцируем ток: el=-LωImcos(ωt+ψu) подать сигналы u и i, то на его экране будет иметь место. . . u – /2 -Lω=X; XI=UL; π/2 = i= el=-ULcos(ωt+ψu) для того чтобы смотреть диаграмму в одной системе Re координат, необходимо перейти к синусу: el=-ULsin(ωt+ψu+ /2) u=ULsin(ωt+ψu+ /2) Так как u и el противоположны по знаку и равны по модулю: u=ULsin(ωt+ψu+ /2)

Переменный ток в ёмкости К конденсатору приложено синусоидальное Im напряжение u(t)=Umsin(ωt+ψ), ток протекающий через него равен: i=dq/dt=C(du/dt)=ωCUmcos(ωt+ψ) UC Используя закон Ома и учитывая что Хс=1/ωC, Векторная диаграмма перепишем ток: i(t)=Imcos(ωt+ψ). Чтобы наблюдать u – /2 = i= - графики в одной системе координат перейдем к синусу: -π/2 i(t)=Imsin(ωt+ψ+ /2) Re Полученный результат показывает, что напряжение на конденсаторе отстает по фазе от тока на /2. I i(t)=Imsin(ωt+ψ+ Таким образом, если на входы двухлучевого /2) осциллографа подать сигналы u и i, то на его экране будет иметь место картинка… C

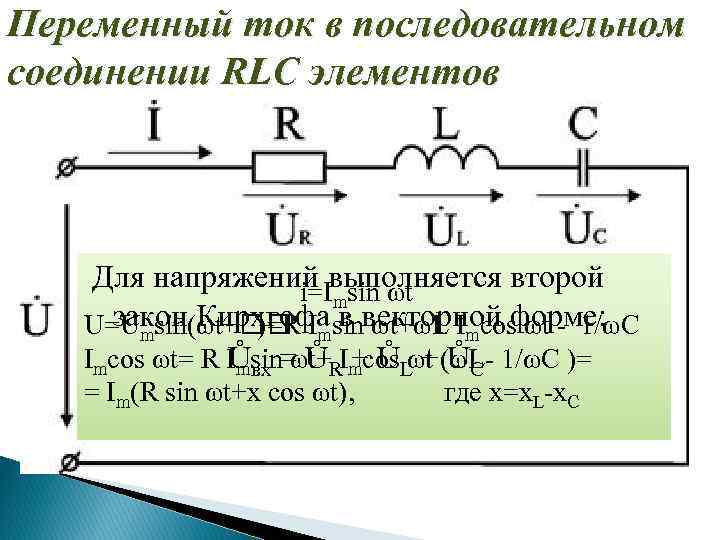
Переменный ток в последовательном соединении RLC элементов Для напряжений выполняется второй i=Imsin ωt закон Кирхгофа в векторной форме: U=Umsin(ωt+ msin ωt+ωL Imcos ωt - 1/ωC )=R I Imcos ωt= R Imsin ωt+ I + ŮL + ŮC Ůвх = ŮR mcos ωt (ωL- 1/ωC )= = Im(R sin ωt+x cos ωt), где х=х. L-x. C

Математическое построение векторных диаграмм угол сдвига фаз равен φ = arctg((XL - XC) / R) (*) В зависимости от величин L и С в формуле (*) возможны следующие варианты: XL > XC; XL < XC; XL = XC Для варианта XL > XC угол φ > 0, UL > UC. Ток отстает от напряжения на угол φ. Цепь имеет активноиндуктивный характер. Векторная диаграмма напряжений имеет вид:

Математическое построение векторных диаграмм Для варианта XL < XC угол φ < 0, UL < UC. Ток опережает напряжение на угол φ. Цепь имеет активно-емкостный характер. Векторная диаграмма напряжений имеет вид: .

Математическое построение векторных диаграмм Для варианта XL = XC угол φ = 0, UL = UC. Ток Этот режим называется резонанс напряжений совпадает с напряжением. Цепь имеет активный (UL = UC). Напряжения на элементах UL и характер. Полное сопротивление z=R UC могут значительно превышать входное наименьшее из всех возможных значений XL и напряжение. Ток так же принимает свое XC. Векторная диаграмма напряжений имеет вид наибольшее значение.

Треугольник напряжений

Параллельное соединении RLC элементов i=i. R+ i. L+ i. C Схема на рисунке подключена на синусоидальное Imsin(ωt- )=1/R Umsin ωt+1/(Lω)Umcos ωt - ωCUmcos ωt= = Umsin[1/R sin ωt +(1/(Lω) - ωC) cos ωt ] = напряжение U=Umsinωt. =Um(g sin ωt-b cos ωt), где b=1/(Lω) - ωC; g=1/R Определим ток на входе схемы. В зависимости от значения проводимости цепь может иметь: индуктивный характер - b. L> b. C В соответствии с первым законом Кирхгофа: i=i. R+ i. L+ i. C емкостной характер - b. L< b. C активный характер - b =b

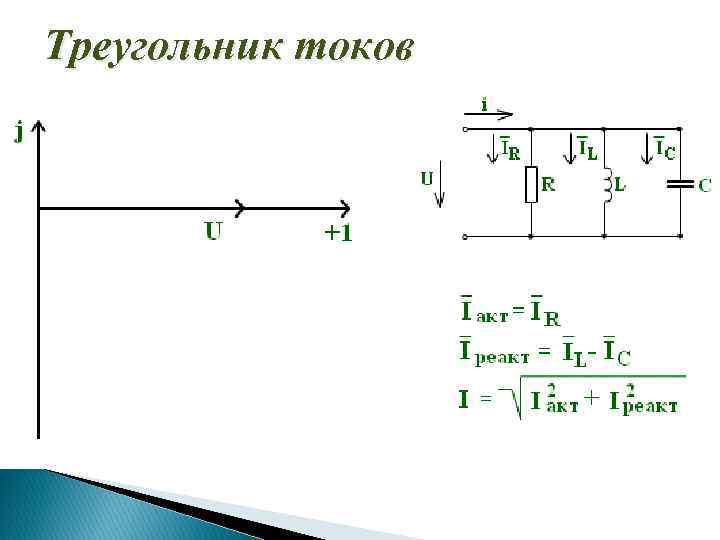
Треугольник токов

Мощность в цепи переменного тока Мгновенной мощностью называют произведение мгновенного напряжения на входе цепи на мгновенный ток. Пусть мгновенные напряжение и ток определяются по формулам: u=Umsin(ωt+ ) и i=Imsin ωt Тогда:

Мощность в цепи переменного тока Среднее значение мгновенной мощности за период: Получим еще одну формулу: Среднее арифметическое значение мощности за период называют активной мощностью и обозначают буквой P. Эта мощность измеряется в ваттах и характеризует необратимое преобразование электрической энергии в другой вид энергии: в тепловую, световую, механическую и пр.

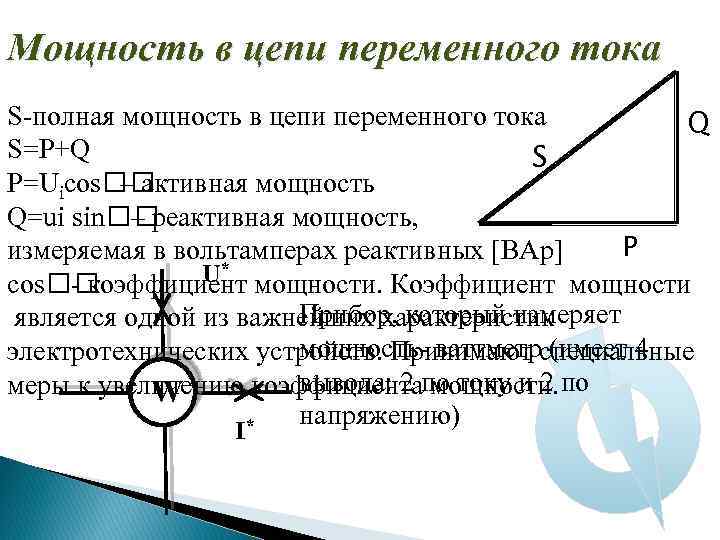
Мощность в цепи переменного тока S-полная мощность в цепи переменного тока Q S=P+Q S P=Uicos – активная мощность Q=ui sin – реактивная мощность, P измеряемая в вольтамперах реактивных [ВАр] U* cos - коэффициент мощности. Коэффициент мощности Прибор, который измеряет является одной из важнейших характеристик мощность- ваттметр (имеет 4 электротехнических устройств. Принимают специальные вывода: 2 по току и 2 по меры к увеличению коэффициента мощности. W напряжению) * I

Мощность в цепи переменного тока Активная мощность не может быть отрицательной. Реактивная мощность является мерой потребления реактивного тока, характеризует процессы обмена между цепью и источником, численно равная максимальной скорости заполнения энергии в цепи. В зависимости от знака угла реактивная мощность может быть как отрицательна, так и положительна. Она характеризует электромагнитную энергию, временно запасенную реактивными элементами в цепи. Активная Р тратится на резисторе безвозвратно, реактивная Q может запасаться.

Баланс комплексной мощности Арифметическая сумма всех комплексно отдаваемых мощностей равна арифметической сумме всех комплексно потребляемых мощностей. При равенстве сумм комплексных величин, суммы их модулей не равны другу => для полных мощностей баланс не соблюдается.

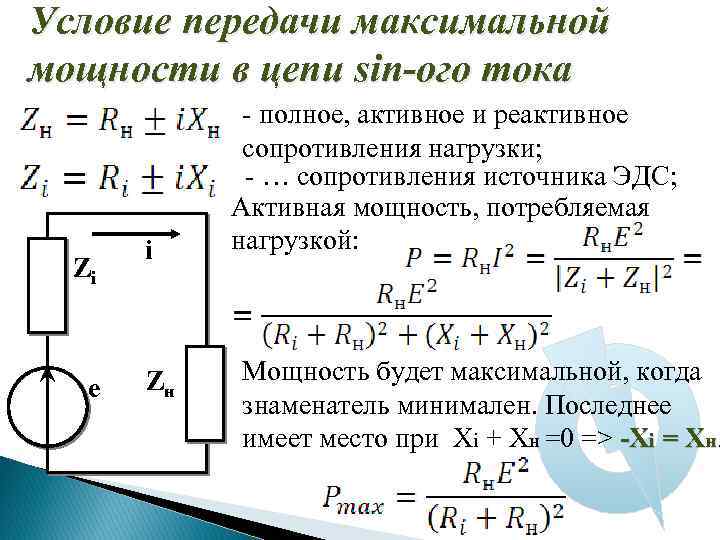
Условие передачи максимальной мощности в цепи sin-ого тока Zi e i Zн - полное, активное и реактивное сопротивления нагрузки; - … сопротивления источника ЭДС; Активная мощность, потребляемая нагрузкой: Мощность будет максимальной, когда знаменатель минимален. Последнее имеет место при Xi + Xн =0 => -Xi = Xн.

Условие передачи максимальной мощности в цепи sin-ого тока Найдем условие передачи максимальной мощности: Предполагая что Rн переменная величина, рассмотрим условие максимума относительно сопротивления нагрузки Откуда Rн=Ri. На основании найденных равенств, заключаем, что условие передачи максимальной активной мощности является: , где Zi*- комплексное сопротивление, сопряженное с Zi. При соблюдении этого условия на нагрузке потребляет мощность:

КПД в цепи синусоидального тока Коэффициент полезного действия для данной схемы: В согласованном режиме: ŋ Половина мощности теряется внутри источника. Поэтому согласованный режим не используется в силовых энергетических цепях.

Явление резонанса Резонанс - режим электрической цепи, при котором входной ток совпадает по фазе с входным напряжением, несмотря на наличие в цепи реактивных элементов. Резонансный режим наступает, когда частота внешних воздействий на систему равна собственной частоте системы: ω=2πf = ω0= 2πf 0. Особенность резонанса - значительное увеличение U или I. Цепь в резонансе характеризуется следующим: входные реактивные сопротивления или проводимости равны нулю: xвх=0; bвх=0; Входная мощность чисто активная: Sвх=Pвх+i. Qвх= Pвх;

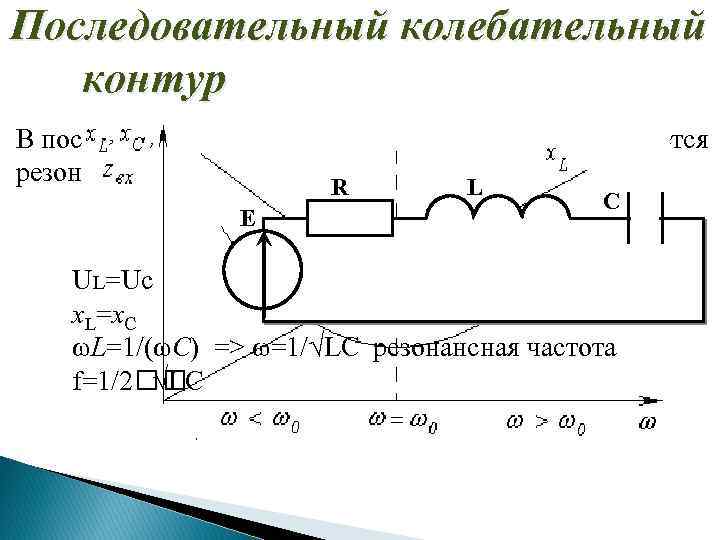
Последовательный колебательный контур В последовательном колебательном контуре наблюдается резонанс напряжений. R L Е C UL=Uc x. L=x. C ωL=1/(ωC) => ω=1/√LC резонансная частота f=1/2 √LC

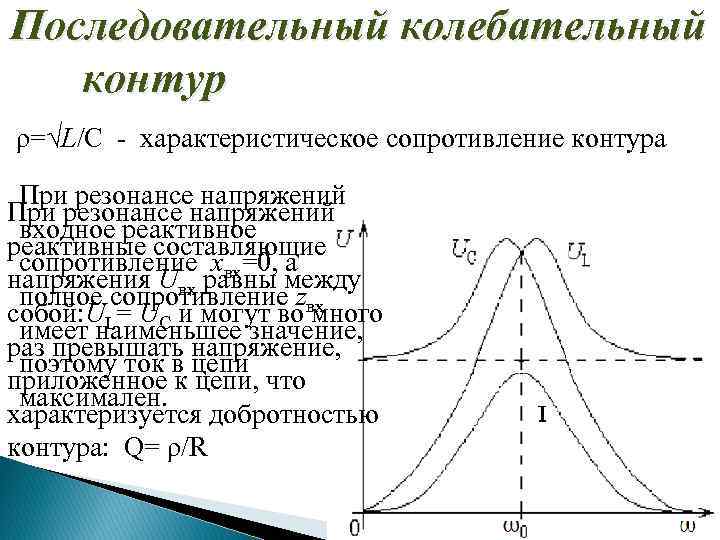
Последовательный колебательный контур ρ=√L/C - характеристическое сопротивление контура При резонансе напряжений входное реактивные составляющие сопротивление xвх=0, а напряжения Uвх равны между полное сопротивление zвх собой: UL= UC и могут во много имеет наименьшее значение, раз превышать напряжение, поэтому ток в цепи приложенное к цепи, что максимален. характеризуется добротностью контура: Q= ρ/R

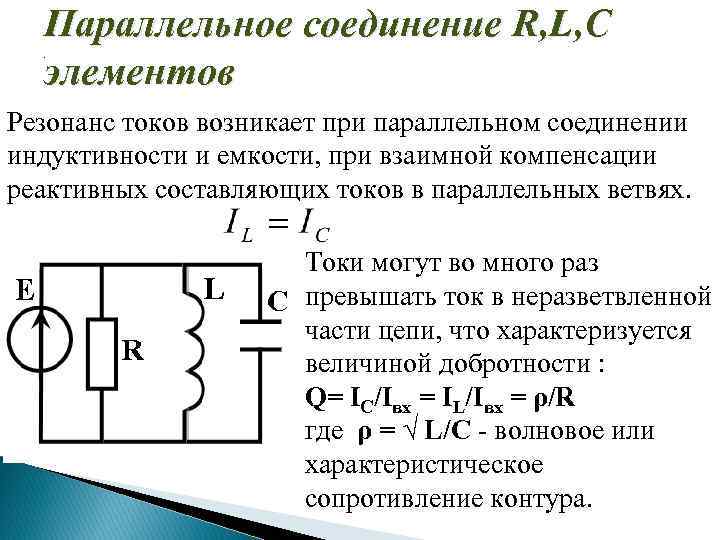
Параллельное соединение R, L, C элементов . Резонанс токов возникает при параллельном соединении индуктивности и емкости, при взаимной компенсации реактивных составляющих токов в параллельных ветвях. Токи могут во много раз превышать ток в неразветвленной части цепи, что характеризуется величиной добротности : Q= IC/Iвх = IL/Iвх = ρ/R где ρ = √ L/C - волновое или характеристическое сопротивление контура.

Энергия в последовательном контуре