Perception of mid frequency and high frequency intermodulation

Perception of mid frequency and high frequency intermodulation distortion in loudspeakers, and its relationship to high -definition audio. (A physicist meets the twilight zone) David Griesinger Lexicon 3 Oak Park Bedford, MA 01730

Why Bother? • What is the relationship between high frequency intermodulation distortion and recordings with frequency response above 20 k. Hz? • Why do my choral recordings sound fuzzy – particularly when played at high level? – And does the perception of “fuzziness” grow more obvious with long-term listening? • Is the short-term A/B test the ultimate “Gold Standard” for audio reproduction? – Is it possible that long-term listening can reveal flaws that go undetected in a short-term A/B test? • This talk will examine the physics and physiology that these questions involve. – We may even suggest a few answers!

High Frequency Intermodulation Distortion and Ultrasonic reproduction • THE essential paper on this subject is: Kiryu and Ashihara “Detection of Threshold for tones above 22 k. Hz. ” – Convention paper 5401 presented at the 110 th Convention, May 12 -15 2001, Amsterdam. – The authors presented 13 subjects with a test signal consisting of a 2 k. Hz tone combined with odd order harmonics, both sonic and ultrasonic. • The ultrasonic harmonics were switched on and off at a 2 Hz rate. – ALL subjects could discriminate the ultrasonics when the combined signal was presented through a single loudspeaker. – NONE of the subjects could discriminate the ultrasonics when each ultrasonic harmonic was reproduced from a separate speaker.

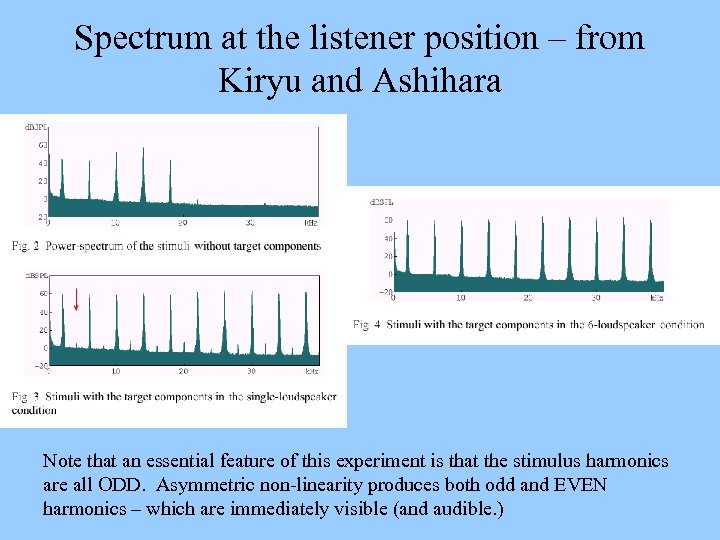Spectrum at the listener position – from Kiryu and Ashihara Note that an essential feature of this experiment is that the stimulus harmonics are all ODD. Asymmetric non-linearity produces both odd and EVEN harmonics – which are immediately visible (and audible. )

Kiryu and Ashihara’s result is strong • Their choice of source signal MAXIMIZES the (possible) audibility of an ultrasonic signal. – The sound pressure of the ultrasonic harmonics are equal to the sound pressure of the harmonics below 20 k. Hz. • For almost all common sound sources the ultrasonics are weaker. • Thus if the ultrasonics are perceived directly through some effect of their presence on nerve firings for the lower harmonics, this signal should produce a positive result. – The use of only odd harmonics for the source signal maximizes the chance that the ultrasonics will be perceived if ANY part of human physiology is (asymmetrically) non-linear. • The basilar membrane is inherently asymmetrically non-linear. The hair cells are half-wave rectifiers. • The probability of finding asymmetric non-linearities in other parts of the system is large.

There was a null result! • When the EXTERNAL non-linearities were eliminated, there was NO ultrasonic perception. – We can conclude that: • The mechanical conduction of ultrasonics to the basilar membrane is either effectively zero, or symmetrically linear. • If significant ultrasonic energy actually reaches the basilar membrane, there are NO hair cells that respond to it. • We will present evidence from other experiments that support these conclusions.

DG experiment – Modulated Harmonics • We wanted to measure the distortion generating mechanism observed by Kiryu and Ashihara by inducing distortion in common tweeters. • Seemed like a simple experiment: – – Make some sweep signals in MATLAB Record a few common instruments with a B&K 4133 microphone Filter out the frequencies below 20 k. Hz Play them back at various levels, and listen.

ENTER – the TWILIGHT ZONE • All I needed was a good quality sound card that would record and playback 96 k. Hz. – Many manufacturers seem to offer such a thing at reasonable prices. I chose one by the most popular manufacturer… let’s call them “C”. • After the usual frustrating two hours to purchase the board, disassemble the computer, install the drivers, call customer service when the drivers crash, download new drivers from the web, etc, • Although you could set the device to record at 96 k. Hz, signals above 23 k. Hz would not record. • Matlab sweeps generated at 96 k. Hz would not play back above 23 k. Hz. • More calls to customer service. Typical conversation: What interrupts is the card using? What video card are you using? What operating system are you using? (Windows 2000 pro. ) OH! That’s your problem – try XP. – So I decided to bite the bullet and upgrade to XP. I also upgraded to the most expensive version of this manufacturer’s sound boards. • But the XP upgrade took longer than expected at the computer shop.

More twilight • I decided to buy a USB based device that did 96/24, as this would be useful for demos from my laptop – such as at this lecture. – But the drivers would not load in my regular laptop, and the customer service had no advice at all. – I tried a different laptop. The drivers loaded fine. Same operating system. (Windows ME. ) – But this external board would also not record or play above 23 k. Hz. – Customer service was again not very helpful. “What interrupts is the USB service routine using? You are actually looking at the output with an oscilloscope!? ” – It’s a good thing I am sometimes known as “Mr. Matrix!”

A bit of light • So I just kept calling customer service until I got an operator who was willing to answer the question “Are ANY of your boards actually capable of operating at 96 k. Hz? ” – After a great deal of waiting on hold the answer came back. – “NO” – “In fact, none of our competitors do either… We all have 96/24 converters, but we run them at 48 k. Hz. ” – What do you suggest that I do… • “Don’t buy consumer – go to pro. ” – So I did. No problem, just much more money.

So – finally to the experiments • C language program was written to generate a twin-tone frequency sweep, broken into tone bursts (so as not to burn out the tweeter. ) • The sweep is repeated with 6 d. B increases in level, so the level dependence of any distortion could be measured.

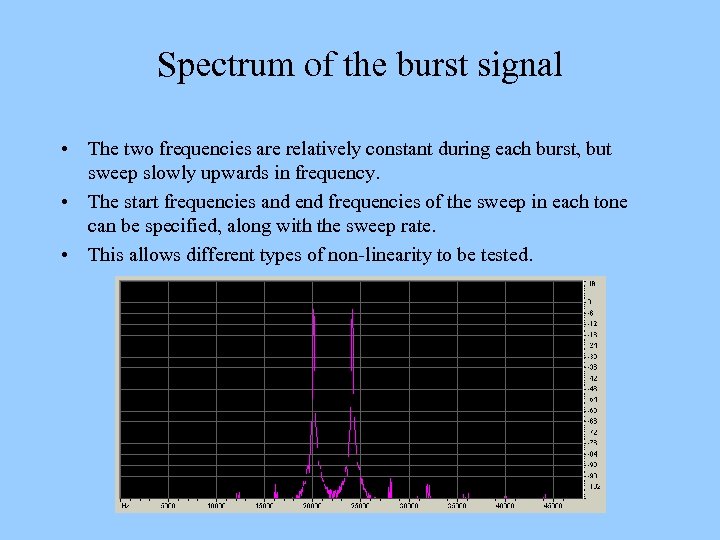Spectrum of the burst signal • The two frequencies are relatively constant during each burst, but sweep slowly upwards in frequency. • The start frequencies and end frequencies of the sweep in each tone can be specified, along with the sweep rate. • This allows different types of non-linearity to be tested.

Result – nothing significant is heard. • Subharmonics of the burst signal can be heard with difficulty… – In a quiet room… • When the ultrasonic level is above 80 d. B SPL at one meter the subharmonics are below 30 d. B SPL, at 15 cm from the tweeter. – The levels of the sub harmonics are consistent with the distortion in the amplifier - ~0. 1 %. • The LOUDSPEAKER seems blameless. – 4 different loudspeakers with different tweeters were tried, with the same result. – The observed harmonics were produced by the amplifier.

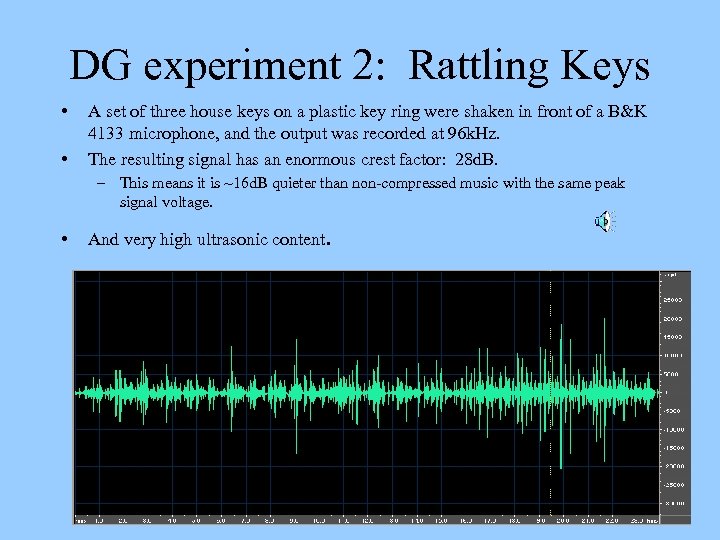DG experiment 2: Rattling Keys • • A set of three house keys on a plastic key ring were shaken in front of a B&K 4133 microphone, and the output was recorded at 96 k. Hz. The resulting signal has an enormous crest factor: 28 d. B. – This means it is ~16 d. B quieter than non-compressed music with the same peak signal voltage. • And very high ultrasonic content.

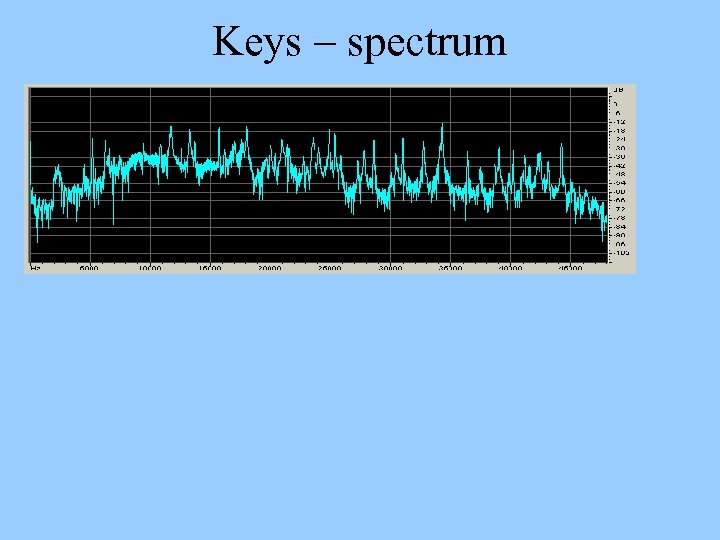Keys – spectrum

Experiment: • Reproduce the signal with and without the ultrasonic component. This was done by low-pass filtering the original signal at 20 k. Hz, and alternating it with the full bandwidth signal. Reproduce only the components above 20 k. Hz and listen for ANY audible sound.

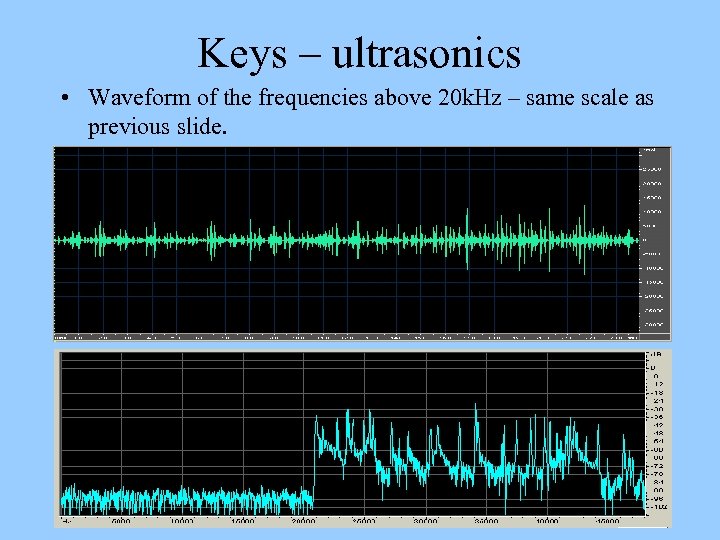Keys – ultrasonics • Waveform of the frequencies above 20 k. Hz – same scale as previous slide.

Result – the same as for bursts • No difference could be heard with and without the ultrasonics – (but the one subject was rather old…) • When the ultrasonic signals only were played at high levels, intermodulation products from the input signals were easily heard - at levels consistent with amplifier distortion.

Conclusions from DG ultrasonic tests • The various tweeters tested – 3 metal dome tweeters and one soft dome tweeter – produce insignificant amounts of intermodulation products below 20 k. Hz when driven by ultrasonic signals. • Amplifier distortion can produce distortion products below 20 k. Hz that are audible (with difficulty) in the absence of other signals below 20 k. Hz. – But with a high quality amplifier these distortion products are not audible in the presence of even extraordinary ultrasonic sources such as rattling keys. – Unless the amplifier is driven into clipping.

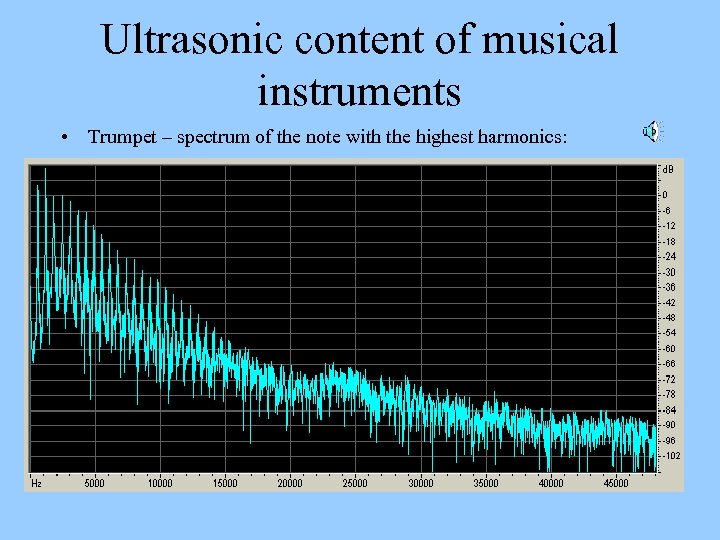Ultrasonic content of musical instruments • Trumpet – spectrum of the note with the highest harmonics:

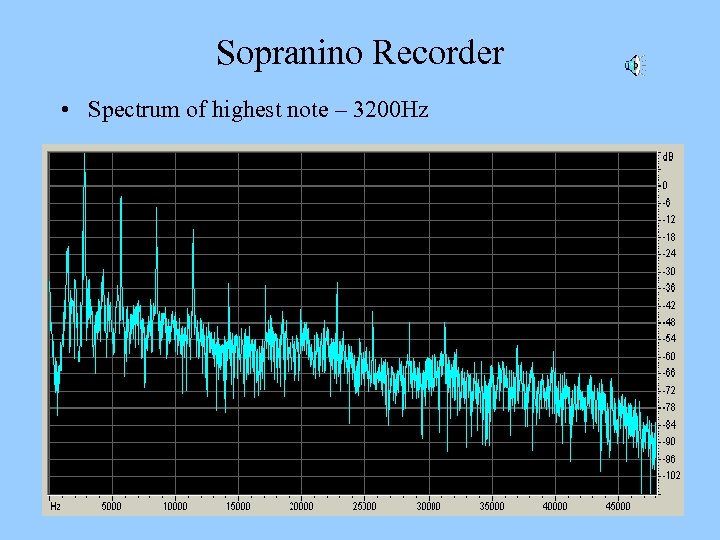Sopranino Recorder • Spectrum of highest note – 3200 Hz

Sopranino Recorder 2 • Although the highest note of the particular sopranino recorder I own produces ultrasonic harmonics – • These harmonics are AT MAXIMUM 40 d. B below the level of the fundamental. – Compare this to the levels used by Kiryu and Ashihara, where the ultrasonic harmonics were equal in level to the fundamentals • Notice also that both even and odd harmonics are present in the sopranino. – So any even order harmonic products will be masked.

Percussion • DG lacks a home drum set. So he went looking for recordings of drums… • MORE TWILIGHT ZONE • I many samplers and examples of SACD and DVD audio disks. • Very few had any popular music that was not resampled from 48 k. Hz. • So I borrowed three more samplers and five SACD disks from John Newton. – None of the popular music samples had anything at all above 23 k. Hz.

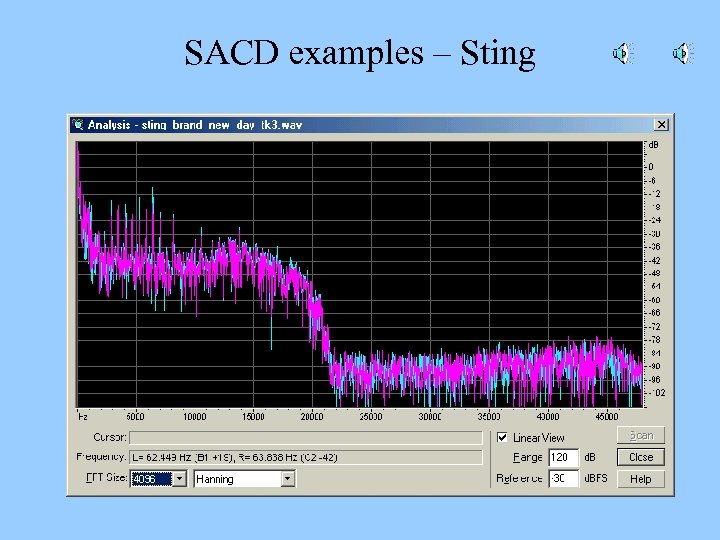SACD examples – Sting

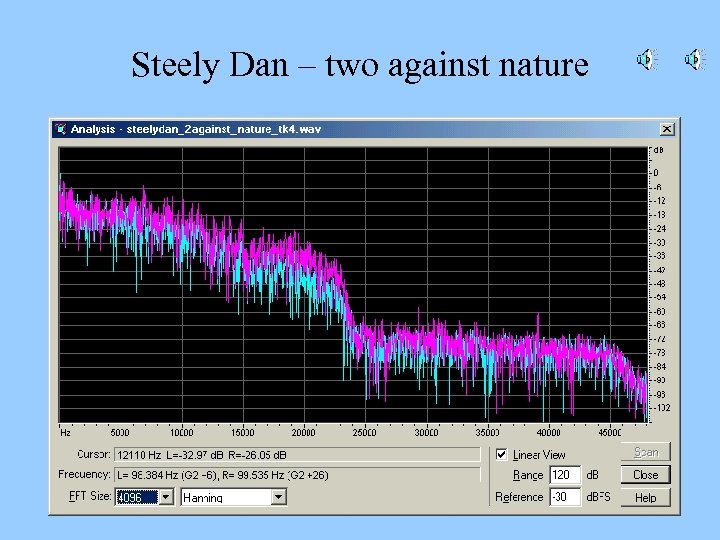Steely Dan – two against nature

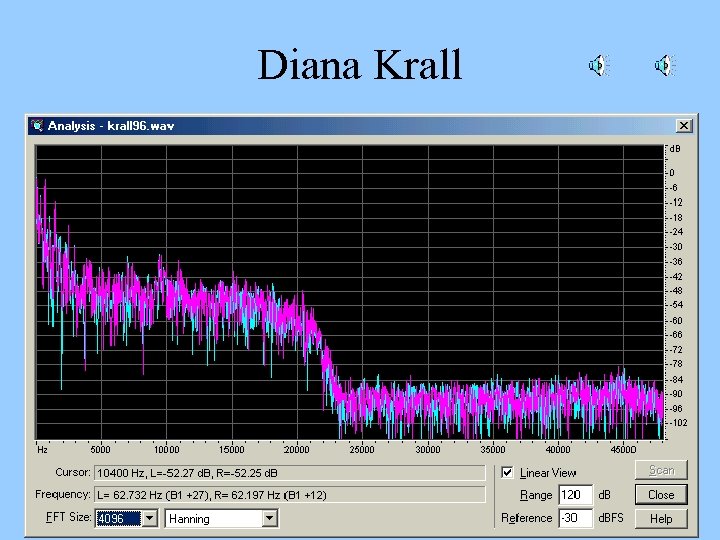Diana Krall

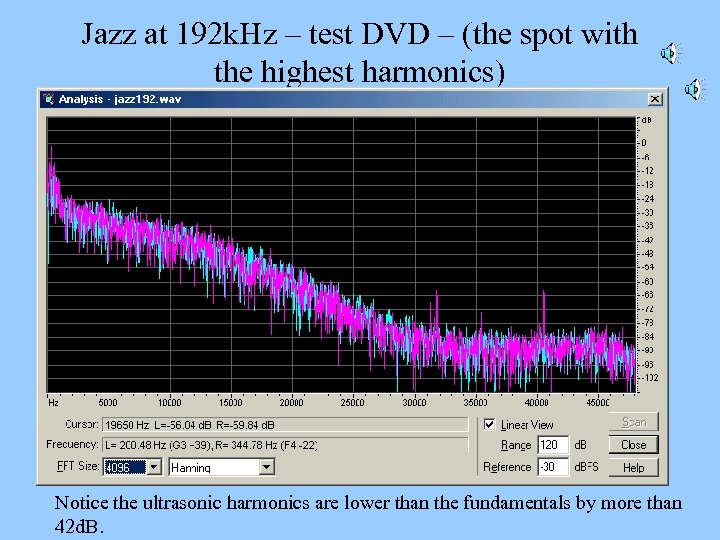Jazz at 192 k. Hz – test DVD – (the spot with the highest harmonics) Notice the ultrasonic harmonics are lower than the fundamentals by more than 42 d. B.

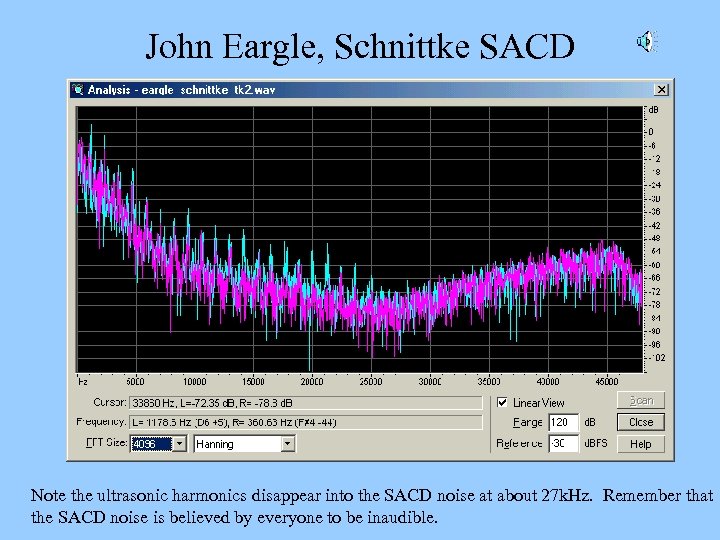John Eargle, Schnittke SACD Note the ultrasonic harmonics disappear into the SACD noise at about 27 k. Hz. Remember that the SACD noise is believed by everyone to be inaudible.

Timing accuracy and information theory. • It is widely believed that the assumed superiority of DVD audio and SACD is improved “resolution” due to improved “timing accuracy. ” • It is well known that human binaural hearing can distinguish timing differences between the ears of as little as two microseconds – This is often taken to imply that the frequency response of the physiological system must extend to 500 k. Hz. • However it is easy to demonstrate that a 1 k. Hz sine tone – modulated with a raised cosine – can be accurately localized, even though the waveform contains NO frequencies above 1400 Hz!

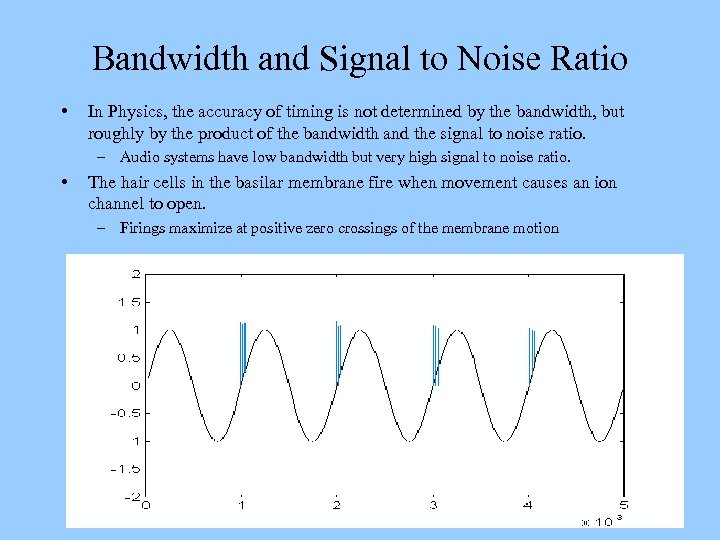Bandwidth and Signal to Noise Ratio • In Physics, the accuracy of timing is not determined by the bandwidth, but roughly by the product of the bandwidth and the signal to noise ratio. – Audio systems have low bandwidth but very high signal to noise ratio. • The hair cells in the basilar membrane fire when movement causes an ion channel to open. – Firings maximize at positive zero crossings of the membrane motion

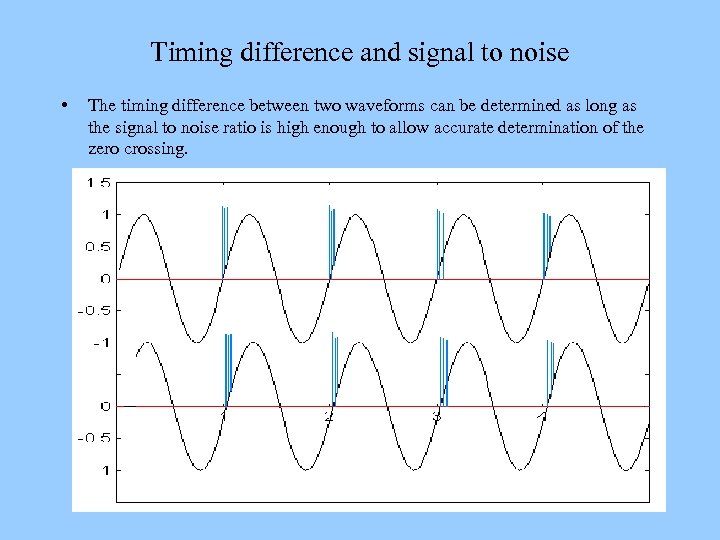Timing difference and signal to noise • The timing difference between two waveforms can be determined as long as the signal to noise ratio is high enough to allow accurate determination of the zero crossing.

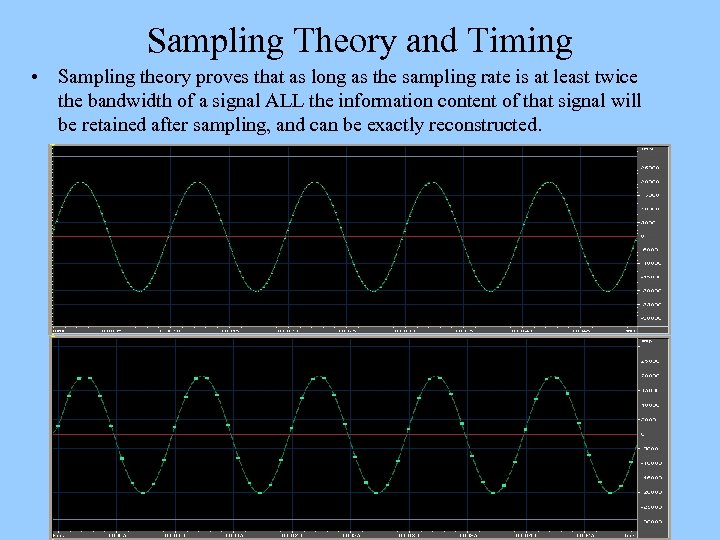Sampling Theory and Timing • Sampling theory proves that as long as the sampling rate is at least twice the bandwidth of a signal ALL the information content of that signal will be retained after sampling, and can be exactly reconstructed.

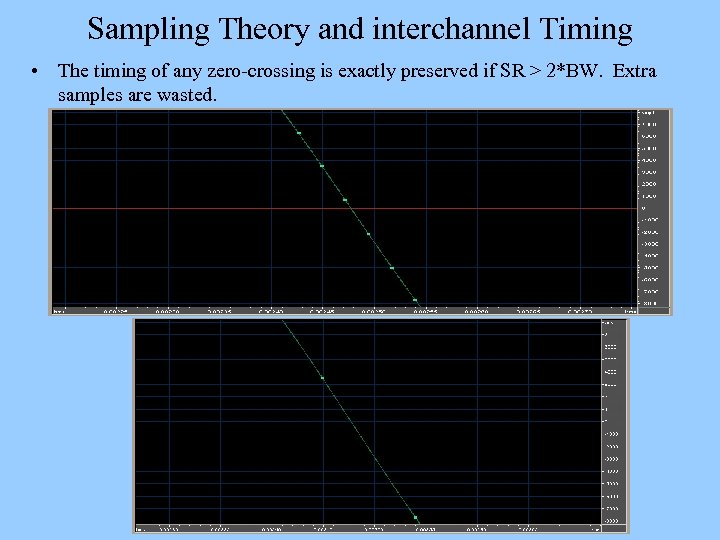Sampling Theory and interchannel Timing • The timing of any zero-crossing is exactly preserved if SR > 2*BW. Extra samples are wasted.

Sampling and reconstruction in practice • • • 10 or more years ago it was difficult to sample signals with sufficient accuracy to approach theoretical ideals. Similarly, reconstruction with practical D/A converters and filters could cause (barely) audible artifacts. The artifacts present in practical converters were reduced at higher sampling rates. – So raising the sampling rate above 48 k. Hz seemed reasonable for the highest quality audio. • Presently integrated A/D and D/A converters are available that sample and reconstruct signals to theoretical limits (at 18 or 20 bit accuracy). • These converters are inexpensive and in wide use. For these converters, there is no advantage to higher sampling rates – unless we can prove that ultrasonic frequencies somehow contribute to human perception. – The author is unaware of any experiment meeting double blind standards that supports this claim.

Absolute timing and Human Physiology • “The human brain is a computer of great sophistication and complexity, with a clock frequency of 1 k. Hz. ” (Hiroshi Riquimaroux) • The author is unaware of any experiment that shows musical timing accuracy in speech or music that is better than about 1 ms. Physiological processes do exist in binaural hearing with interchannel timing accuracies down to 2 microseconds, but this is not the same thing as long term timing accuracy over fractions of a second. These interchannel timing differences are exactly preserved at common sampling rates. • • • Hiroshi’s comment pretty much sums it up!

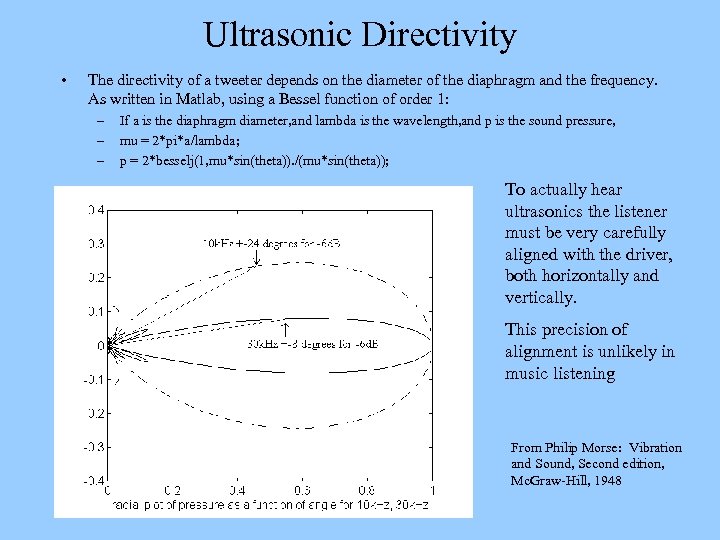Ultrasonic Directivity • The directivity of a tweeter depends on the diameter of the diaphragm and the frequency. As written in Matlab, using a Bessel function of order 1: – – – If a is the diaphragm diameter, and lambda is the wavelength, and p is the sound pressure, mu = 2*pi*a/lambda; p = 2*besselj(1, mu*sin(theta)). /(mu*sin(theta)); To actually hear ultrasonics the listener must be very carefully aligned with the driver, both horizontally and vertically. This precision of alignment is unlikely in music listening From Philip Morse: Vibration and Sound, Second edition, Mc. Graw-Hill, 1948

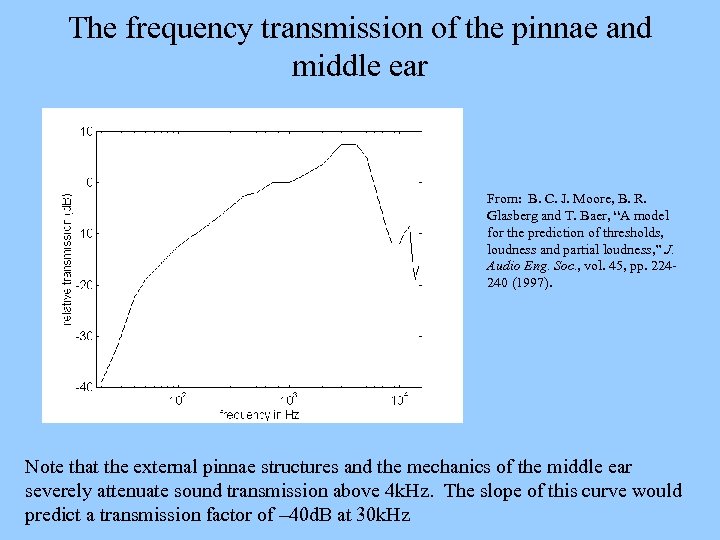The frequency transmission of the pinnae and middle ear From: B. C. J. Moore, B. R. Glasberg and T. Baer, “A model for the prediction of thresholds, loudness and partial loudness, ” J. Audio Eng. Soc. , vol. 45, pp. 224240 (1997). Note that the external pinnae structures and the mechanics of the middle ear severely attenuate sound transmission above 4 k. Hz. The slope of this curve would predict a transmission factor of – 40 d. B at 30 k. Hz

Conclusions for “High Definition” Audio: • Adding ultrasonics to a recording technique does NOT improve time resolution of typical signals – either for imaging or precision of tempo. The presumption that it does is based on a misunderstanding of both information theory and human physiology. • Kiryu and Ashihara have shown that ultrasonic harmonics of a 2 k. Hz signal are NOT audible in the absence of external (non-human) intermodulation distortion. Their experiments put a limit on the possibility that a physiological nonlinearity can make ultrasonic harmonics perceptible. They find that such a non -linearity does not exist at ultrasonic sound pressure levels below 80 d. B. All commercial recordings tested by the author as of 6/1/03 contained either no ultrasonic information, or ultrasonic harmonics at levels more than 40 d. B below the fundamentals. Our experiments suggest that the most important source of audible intermodulation for ultrasonics is the electronics, not in the transducers. Some consumer grade equipment makes a tacit admission of the inaudibility of frequencies above 22 k. Hz by simply not reproducing them. Yet the advertising for these products claims the benefits of “higher resolution. ” Even assuming ultrasonics are audible, loudspeaker directivity creates an unusually tiny sweet spot, both horizontally and vertically. • • •

Mid-Frequency Intermodulation distortion or “why do my loudspeakers sound fuzzy? • Problem: – Loudspeaker reproduction of massed chorus and orchestra is often perceived (by the author) as harsher than the live chorus. – The degree of harshness seemed to depend on the loudspeaker type, and on the playback level. • It seemed worthwhile to investigate whether this perception could be related to intermodulation distortion.

The validity of short duration A/B tests • Floyd Toole has established a protocol for loudspeaker evaluation that allows rapid comparison of two loudspeakers in the identical acoustical location. • Tests using this protocol have proven to be reliable, in that they consistently rank-order loudspeakers in a way that is robust for different listeners and for repeated tests. • But it is not clear that rapid A/B tests are the ideal way to test for intermodulation distortion, which may require a period of time to be perceived. – In a rapid A/B test the primary perception is loudness. – Once loudness has been controlled, differences in frequency response and timbre dominate the result. • Human hearing adapts to errors in spectrum and timbre over a period of 10 to 20 minutes. – Even an old fashioned phonograph sounds pretty good once you get used to it! – And many of the monitoring loudspeakers in common use are severely colored. The people who use them say they sound fine. • Is it possible that after adapting to spectrum and timbre intermodulation problems might become more apparent?

Test Signals We wanted test signals that would mimic the levels and frequencies found in choral and orchestral music. This music typically has fundamentals in the range of 100 Hz to 1000 Hz, with substantial high-order harmonics. The mix of fundamentals and harmonics are related by common musical intervals. A sweep signal consisting of two or more pitches was chosen, where the pitch intervals was held constant. Preliminary tests showed that the harmonic content of the chosen pitches did not significantly affect either the measured or perceived amount of intermodulation distortion Eventually a minor triad was chosen as a test signal. The signal consists of three equal amplitude sine waves. A root, the minor third above, and the fifth above the root. The minor third was chosen as even tempered, and the fifth was chosen to be perfect. Thus a sweep would consist of a frequency f 0 which sweeps from 250 Hz to 4 k. Hz, in combination with f 1 = 1. 1225*f 0, in combination with f 2 = 1. 5*f 0.

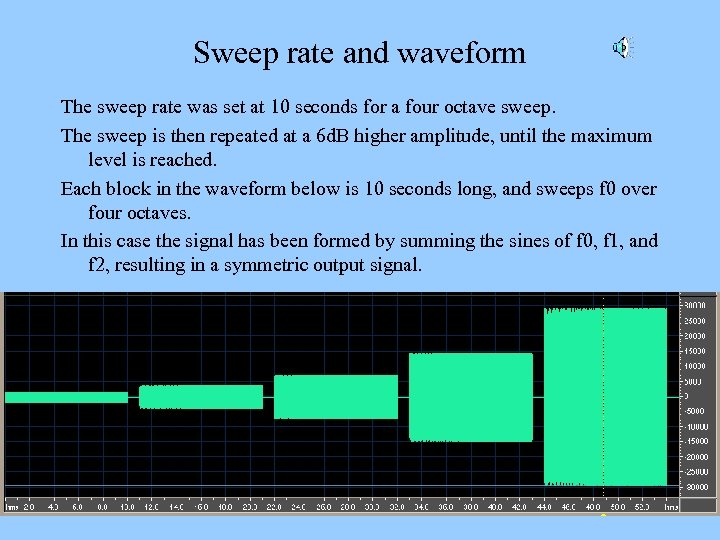Sweep rate and waveform The sweep rate was set at 10 seconds for a four octave sweep. The sweep is then repeated at a 6 d. B higher amplitude, until the maximum level is reached. Each block in the waveform below is 10 seconds long, and sweeps f 0 over four octaves. In this case the signal has been formed by summing the sines of f 0, f 1, and f 2, resulting in a symmetric output signal.

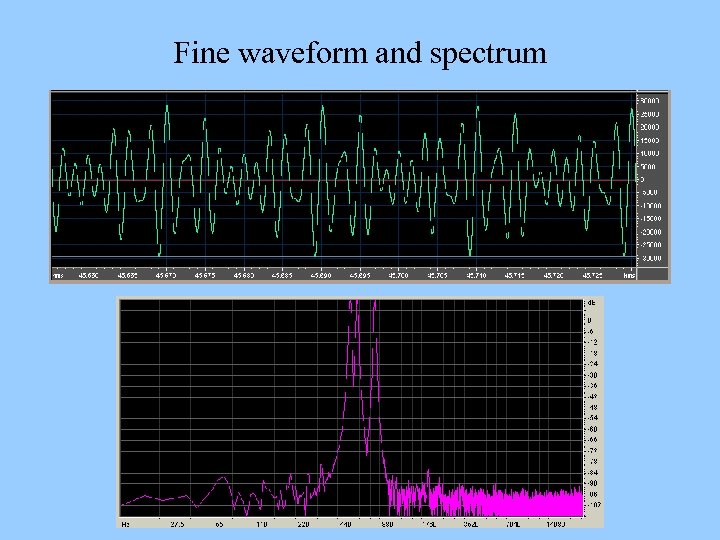Fine waveform and spectrum

Result – speaker 1 Typical output spectrum at the highest level.

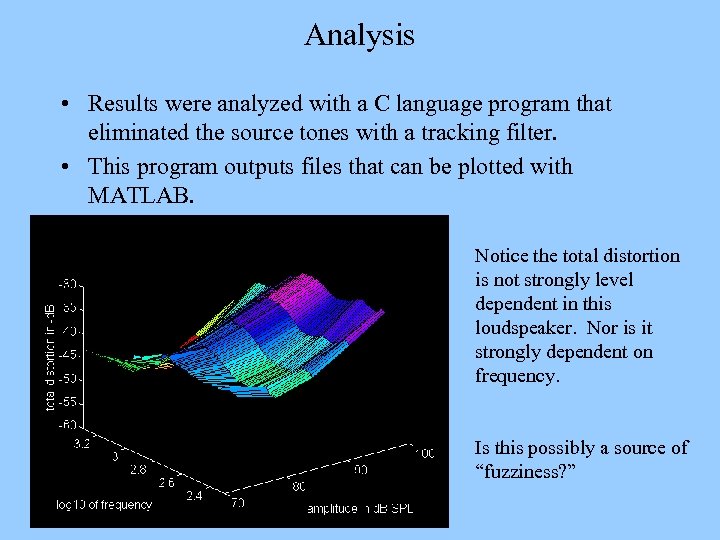Analysis • Results were analyzed with a C language program that eliminated the source tones with a tracking filter. • This program outputs files that can be plotted with MATLAB. Notice the total distortion is not strongly level dependent in this loudspeaker. Nor is it strongly dependent on frequency. Is this possibly a source of “fuzziness? ”

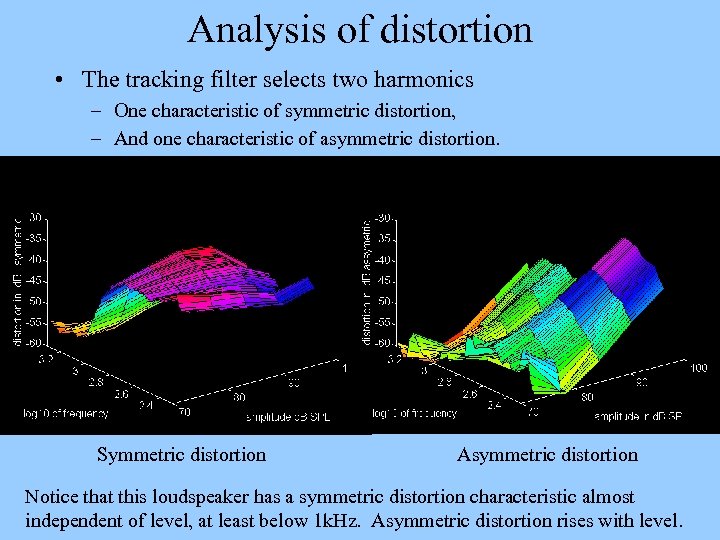Analysis of distortion • The tracking filter selects two harmonics – One characteristic of symmetric distortion, – And one characteristic of asymmetric distortion. Symmetric distortion Asymmetric distortion Notice that this loudspeaker has a symmetric distortion characteristic almost independent of level, at least below 1 k. Hz. Asymmetric distortion rises with level.

Is the observed distortion audible? • The observed distortion is audible on the test signal, particularly on the high level segment. But only if the test subject wears earplugs. • Distortion is audible on the lower level portions also, and it seems relatively independent of level. • But is the perceived distortion in the speaker – or is it in the listener? • As a test, the same signal was reproduced through three loudspeakers, one for each frequency, f 0, f 1, and f 2. – The perception was subtly different when the signals were combined and reproduced through a single loudspeaker. – But these differences could be ascribed to the non-anechoic conditions of the test.

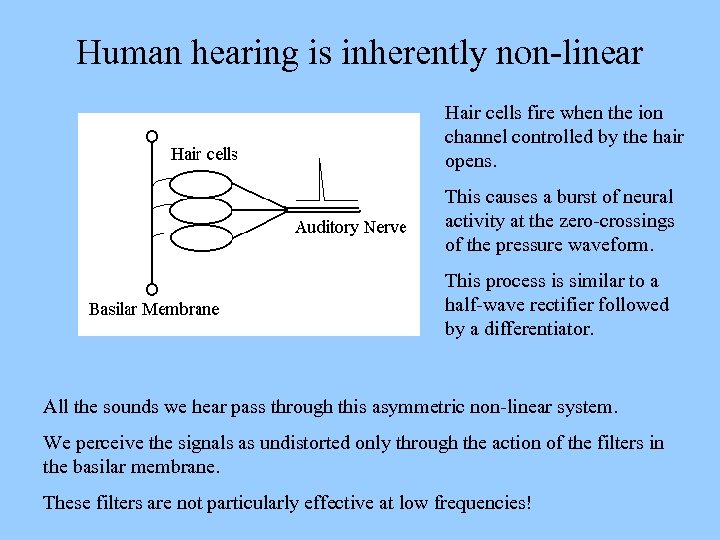Human hearing is inherently non-linear Hair cells fire when the ion channel controlled by the hair opens. This causes a burst of neural activity at the zero-crossings of the pressure waveform. This process is similar to a half-wave rectifier followed by a differentiator. All the sounds we hear pass through this asymmetric non-linear system. We perceive the signals as undistorted only through the action of the filters in the basilar membrane. These filters are not particularly effective at low frequencies!

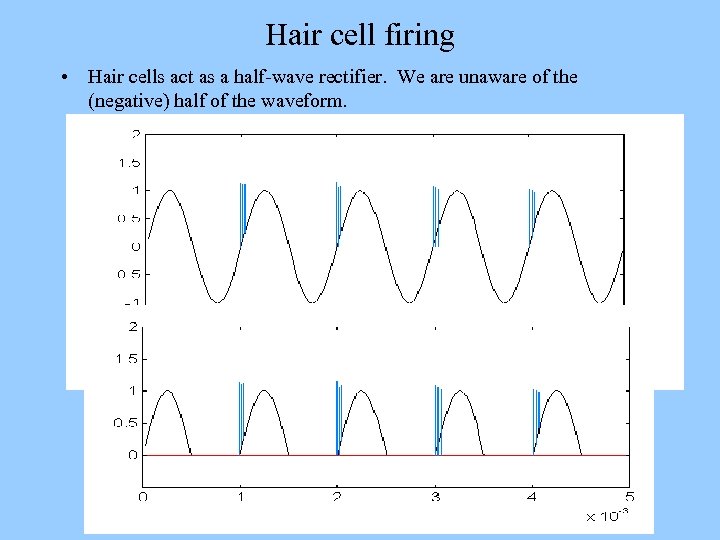Hair cell firing • Hair cells act as a half-wave rectifier. We are unaware of the (negative) half of the waveform.

Result of the half-wave rectification: • The pitch of low frequencies is determined not through the basilar membrane filters, but through the time intervals between nerve firings. • Consequently we cannot distinguish between real frequencies and subharmonics generated through the half-wave rectification process. – This leads to the well-known phenomenon of “false bass” • Listening to two tones that are harmonically related will often produce the perception of the fundamental. For example, a tone at 50 Hz will be heard when 100 Hz and 150 Hz are played together. • Complex low frequency signals, such as a minor triad, are heard as an un-interpretable mix of fundamentals and harmonics. – Composers – outside of grundge rock – tend to avoid them!

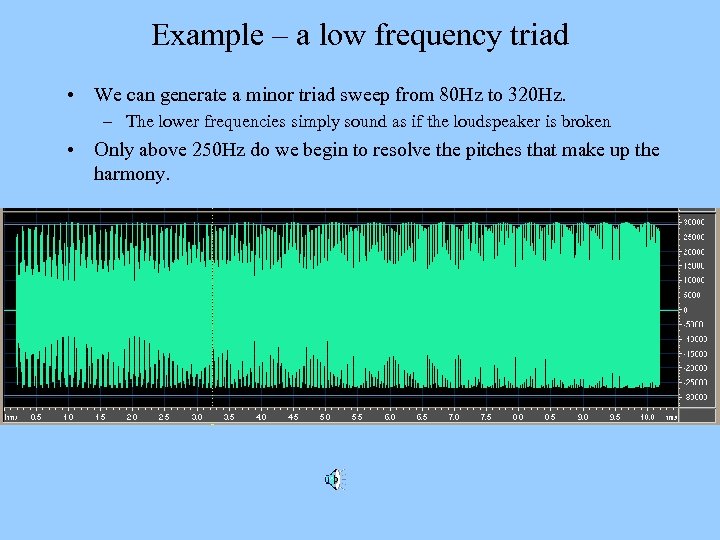Example – a low frequency triad • We can generate a minor triad sweep from 80 Hz to 320 Hz. – The lower frequencies simply sound as if the loudspeaker is broken • Only above 250 Hz do we begin to resolve the pitches that make up the harmony.

Distortion Models - symmetric • We need a mathematical model for loudspeaker distortion that will allow us to find the “just noticeable level” at which distortion becomes perceivable. • After a great deal of head-scratching two simple models were chosen: • 1. Symmetric compression – where delta is typically ~0. 1 or less: – – If the signal voltage is positive Vout = exp((1 -delta)*log(Vin) If the signal voltage is negative Vout = -exp((1 -delta)*log(abs(Vin)) • This distortion is identical to a uniform compression of the waveform. If delta = 0. 1, then the waveform is compressed by 1 d. B for every 10 d. B of level increase. • The advantage of this model is that the percentage distortion is independent of the signal level and spectrum. – There is a small dependence on crest factor.

Distortion Models – asymmetric • • A simple asymmetric distortion model can be created by using a different gain for the positive and negative signal voltages. If the signal voltage is positive: – Vout = (1 -delta_a)*Vin; • If the signal voltage is negative: – Vout = Vin; • This model also produces a distortion that is independent of level and spectrum. • A C language program was written that applies these two distortions to a stereo input file, measures the resulting percentage of distortion, and outputs the distortion only as a stereo file. • This program allows us to listen to the result of the distortion process on a wide variety of input signals. Since the distortion alone is the output, various distortion percentages can be created by simply mixing the distortion with the original signal.

Distortion test with Cool-Edit Here is a segment from the Faure Requiem, repeated once Here is the same signal with delta = 0. 05 and adelta = 0. 03. The distortion has been amplified 20 d. B and the original signal removed.

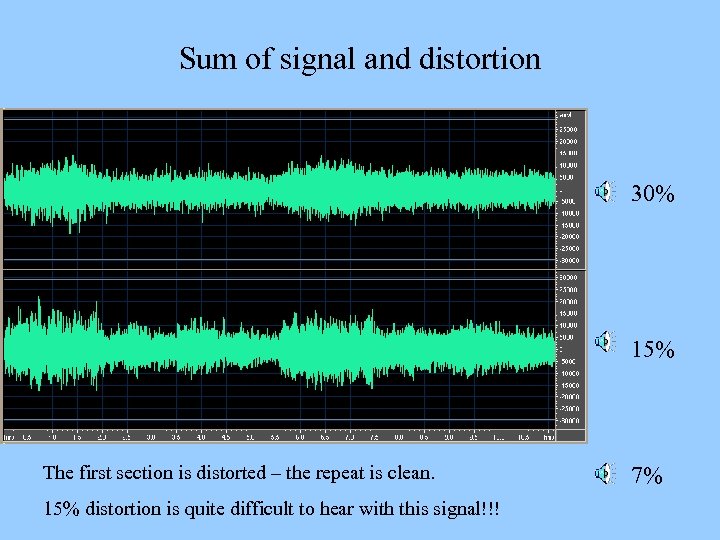Sum of signal and distortion 30% 15% The first section is distorted – the repeat is clean. 15% distortion is quite difficult to hear with this signal!!! 7%

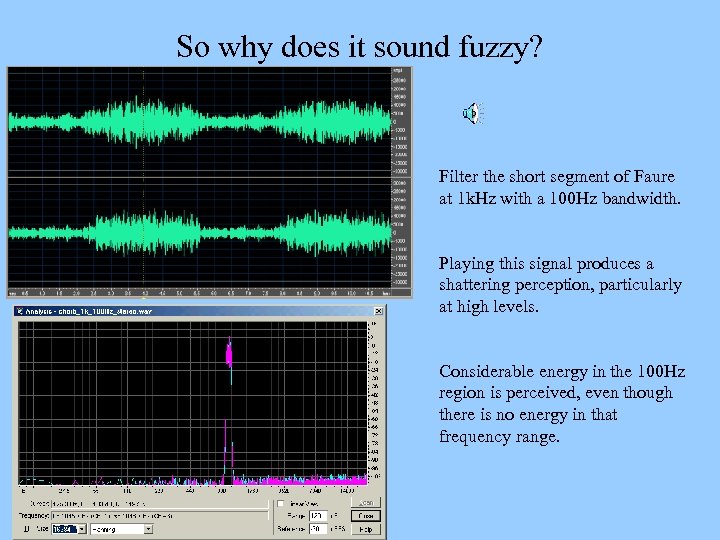So why does it sound fuzzy? Filter the short segment of Faure at 1 k. Hz with a 100 Hz bandwidth. Playing this signal produces a shattering perception, particularly at high levels. Considerable energy in the 100 Hz region is perceived, even though there is no energy in that frequency range.

Result – hair-cell distortion produces the perception of shattering • Explaination: – A 100 Hz bandwidth noise-like signal at 1 k. Hz creates intermodulation products in the 100 Hz region when passed through an asymmetric detector. – These subharmonics may excite the neural sensors for low frequencies directly through motion of the basilar membrane. – They also might be directly perceived by correlation detectors in the 1 k. Hz neural channels. • As the frequency is raised above 1 k. Hz both detection mechanisms will be less active. – In fact, a 4 k. Hz signal with a 100 Hz bandwidth produces very little shattering, and few perceptual subharmonics. – A 4 k. Hz signal with a 400 Hz bandwidth sounds pretty bad.

Shattering at high frequencies • Try an 8 k. Hz signal with a 250 Hz bandwidth: • How about 18 k. Hz and a 500 Hz bandwidth? • How about 15 k. Hz and 500 Hz bandwidth?

Converter Intermodulation • Very inexpensive converters can have high intermodulation distortion at high frequencies – For example, the converters in this laptop. • Example – 15 k. Hz 500 Hz bandwidth as output from this laptop.

Conclusions – fuzzy speakers • The loudspeakers tested have intermodulation distortion lower than the threshold of detection for complex tones. • Non-linear distortion in human hearing appears to account for the audible distortion in full chorus. – The non-linearities – particularly at high frequencies may be a form of age-related hearing loss. – This type of distortion may be well understood by researchers in the fields of hearing and speech, or hearing pathology.

Conclusions: A/B tests • No evidence was uncovered in this study that would invalidate rapid, blind, A/B tests as the gold standard for audio research. • But the possibility remains… – Particularly in the study of room acoustics • intelligibility, muddiness, and envelopment all may depend on the time period devoted to listening to a particular acoustic signal.