d68cc7234b4c8062ea478676b192eda8.ppt
- Количество слайдов: 19

PEGASOS Primal YASSO = sub-Gr. Adient SOlver for SVM Efficient Yet Another Svm SOlver Shai Shalev-Shwartz Yoram Singer Nati Srebro The Hebrew University Jerusalem, Israel

Support Vector Machines QP form: More “natural” form: Regularization term Empirical loss 2

Outline • Previous Work • The Pegasos algorithm • Analysis – faster convergence rates • Experiments – outperforms state-of-the-art • Extensions • kernels • complex prediction problems • bias term 3

Previous Work • Dual-based methods • Interior Point methods • Memory: m 2, time: m 3 log(1/ )) • Decomposition methods • Memory: m, Time: super-linear in m • Online learning & Stochastic Gradient • Memory: O(1), Time: 1/ 2 (linear kernel) Better. Memory: finite 2 dimensional 4 (non-linear kernel) • rates for 1/ , Time: 1/ instances (Murata, Bottou) Typically, online learning algorithms do not converge to the optimal solution of SVM 4
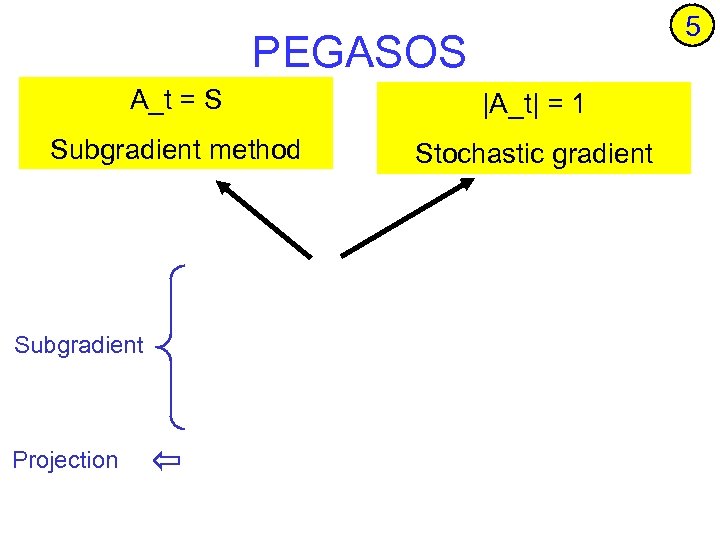
5 PEGASOS A_t = S |A_t| = 1 Subgradient method Stochastic gradient Subgradient Projection

Run-Time of Pegasos • Choosing |At|=1 and a linear kernel over Rn Run-time required for Pegasos to find accurate solution w. p. ¸ 1 - • Run-time does not depend on #examples • Depends on “difficulty” of problem ( and ) 6

Formal Properties • Definition: w is accurate if • Theorem 1: Pegasos finds accurate solution w. p. ¸ 1 - after at most iterations. • Theorem 2: Pegasos finds log(1/ ) solutions s. t. w. p. ¸ 1 - , at least one of them is accurate after iterations 7

Proof Sketch A second look on the update step: 8

Proof Sketch • Lemma (free projection): • Logarithmic Regret for OCP (Hazan et al’ 06) • Take expectation: • f(wr)-f(w*) ¸ 0 Markov gives that w. p. ¸ 1 - • Amplify the confidence 9

Experiments • 3 datasets (provided by Joachims) • Reuters CCAT (800 K examples, 47 k features) • Physics Ar. Xiv (62 k examples, 100 k features) • Covertype (581 k examples, 54 features) • 4 competing algorithms • • SVM-light (Joachims) SVM-Perf (Joachims’ 06) Norma (Kivinen, Smola, Williamson ’ 02) Zhang’ 04 (stochastic gradient descent) • Source-Code available online 10
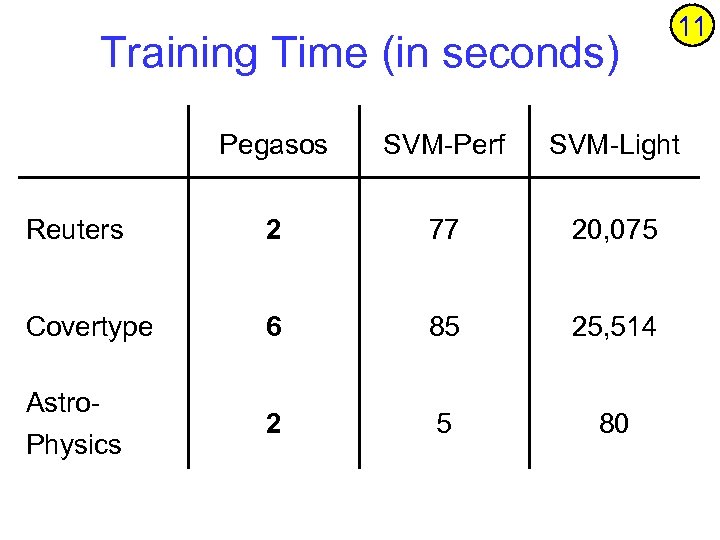
Training Time (in seconds) 11 Pegasos SVM-Perf SVM-Light Reuters 2 77 20, 075 Covertype 6 85 25, 514 2 5 80 Astro. Physics

Compare to Norma (on Physics) obj. value test error 12

Objective Compare to Zhang (on Physics) But, tuning the parameter is more expensive than learning … 13

Objective Effect of k=|At| when T is fixed 14

Objective Effect of k=|At| when k. T is fixed 15

I want my kernels ! • Pegasos can seamlessly be adapted to employ non-linear kernels while working solely on the primal objective function • No need to switch to the dual problem • Number of support vectors is bounded by 16

Complex Decision Problems 17 • Pegasos works whenever we know how to calculate subgradients of loss func. l(w; (x, y)) • Example: Structured output prediction • Subgradient is (x, y’)- (x, y) where y’ is the maximizer in the definition of l

bias term • Popular approach: increase dimension of x Cons: “pay” for b in the regularization term • Calculate subgradients w. r. t. w and w. r. t b: Cons: convergence rate is 1/ 2 • Define: Cons: |At| need to be large • Search b in an outer loop Cons: evaluating objective is 1/ 2 18

Discussion 19 • Pegasos: Simple & Efficient solver for SVM • Sample vs. computational complexity • Sample complexity: How many examples do we need as a function of VC-dim ( ), accuracy ( ), and confidence ( ) • In Pegasos, we aim at analyzing computational complexity based on , , and (also in Bottou & Bousquet) • Finding argmin vs. calculating min: It seems that Pegasos finds the argmin more easily than it requires to calculate the min value
d68cc7234b4c8062ea478676b192eda8.ppt