Pécsi Tudományegyetem Pollack Mihály Műszaki Kar Műszaki Informatika

Pécsi Tudományegyetem Pollack Mihály Műszaki Kar Műszaki Informatika Szak Data Mining 28. Előadás Dr. Pauler Gábor, Egyetemi Docens PTE-PMMFK Villamos Intézet Számítástechnika Tanszék Iroda: Boszorkány u. , B épület 101 Tel: 72/503 -650/3725 E-mail: gjpauler@acsu. buffalo. edu Készült a PTE Alapítvány támogatásával

Az előadás tartalma A Fuzzy Rendszerek alapfogalmai • 28. 1 PÉLDA: Fuzzy jelenségek a gyakorlatban: Mit ábrázol a kép? • 28. 2 PÉLDA: Fuzzy jelenségek a gyakorlatban: Egy kis izgalom • Fuzzy logika • A Fuzzy rendszerek előnyei és hátrányai • A Fuzzy rendszerek története • A bizonytalanság ideáltípusai A Fuzzy Rendszerek alkotóelemei • A Fuzzy halmaz • A tagságfüggvény fajtái • A fuzzy nyelvi változó Fuzzy nyelvi változók kreációja • Egyenlő intervallumok módszere • Parciális gyakorisági hisztogrammok módszere • Klasztercentrumok módszere • Átlapolás • A tagságfüggvények fajtájának kiválasztása • Speciális tagságfüggvényű szélső fuzzy értékek használata Fuzzy szabályok • Feltételi rész • Fuzzy szabálysúly • Következtetési rész Fuzzy következtetési mechanizmus • Kompozíciós módszerek • Dekompozíciós módszerek • Példa a vezérlési függvény modellezésére

A Fuzzy Rendszerek alapfogalmai 1 A Fuzzy rendszer (Fuzzy System): Eloszlásfüggetlen becslési rendszer (Distribution Free Estimator), amely: • Nem tesz előfeltételezéseket a viszonylag kis számú (általában 3. . 8 db) input/output változó (I/O Variables) alkotta döntési térben (Decision Space) lévő eloszlásról • (Pl. egy konténerdaru vezérlésénél a célpontig visszalévő távolság (Distance), és a drótkötél állásszöge (Angle) az input változó, a konténer lengésmentes megállításához szükséges motorerő (Power) az output változó) • Képes az I/O változók kapcsolatát leíró erősen nemlineáris, nem monoton, nem folytonos Vezérlési függvény (Control Function) modellezésére, • A döntési térben, mint azonos univerzumon (Common Universe) felírt, biztosan bekövetkező (Deterministic), életlenül definiált határú (Non-crisp), egymást átlapoló (Overlapping) Fuzzy szabályok (Fuzzy Rules) közti, • Nemlineáris interpoláció (Nonlinear Interpolation) segítségével. • Jóval kevesebb szabállyal képes leírni azonos komplexitású problémát, mint egy éles (Crisp) szabályalapú rendszer Power Distance Angle

28. 1 PÉLDA: Fuzzy jelenségek a gyakorlatban: Mit ábrázol a kép? • • Mivel a fuzzy technologiával kapcsolatban rengeteg tévhit és előítélet van forgalomban, Illetve a fuzzy terminológia is elég félrevezető (pl. a „Fuzzy” szó maga zavarost, kétértelműt jelent) Az elméleti fejtegetések előtt két elgondolkoztató példát adunk a fuzzy működésére Ha nem jövünk rá, mit ábrázol a kép, nézzük hunyorítva, vagy messzebbről:

28. 1 PÉLDA: Fuzzy jelenségek a gyakorlatban: Mit ábrázol a kép? • • • Mikor a képet nem látjuk olyan jól, mint közvetlen közelről, rögtön rájövünk, hogy két házat ábrázol egy parkban, ahol fák is vannak. Ez a jelenség látszólag ellentmond az információ- és kódelmélet alapelveinek: valamit akkor ismerünk fel, ha a kommunikációs csatornában nő a zaj mennyisége? ! A 32× 32 -es 256 színű, 1024 byte-on tárolható kép (ekkora felbontású egy Windows ikon) közelről nézve egyáltalán nem felismerhető, mert nincsen „pontosan, élesen” megrajzolva. Rajzoljuk meg ugyenezt a témát „szép pontosan, élesen”, pl. Auto. CAD-ben: „Feladat: Rajzoljon egy négyzet alakú képet, amelyen két sátortetős földszintes épület látható, a tőlünk távolabbi téglalaprajzú, a közelebbi L-alaprajzú, melynek hosszabbik szára párhuzamos a téglalap alakúval, rövidebb szára a téglalap alakú épület felé fordul. A képen az épületek hossztengelyével párhuzamos Y tengely +30 fokkal, a Z tengely +45 fokkal van elforgatva. Az épületek hosszabbik szárának középpontjában egy-egy ajtó néz felénk, az épületek mögött fák vannak, az épületek közti térköz az épületek szélességének 1. 5 -szöröse. A talaj színe zöld, a fák zöldek, az épületek falai sárgák, a tetejük piros” Ha ezt megrajzoljuk, és lekicsinyítjük a vektorgrafikát, úgy hogy a levetített kép beleférjen 32× 32 -es felbontásba, valami ilyesmit kapunk: Az a bosszantó, hogy ez ugyanúgy 1024 byte-ot fogyaszt, mint az eredeti kép, mégis messze nem olyan élethű, mint az messziről nézve. Valamint, mind a kép részletes szöveges leírása, mind a vektorgrafikát tároló Auto. CAD *. SHP fájl mérete meghaladja az 1024 byte-ot… Hogyan lehetséges, hogy egy „pontatlanul, életlenül” ábrázolt valami azonos méretben több információt tárol, mint a „pontos” leírások? ?

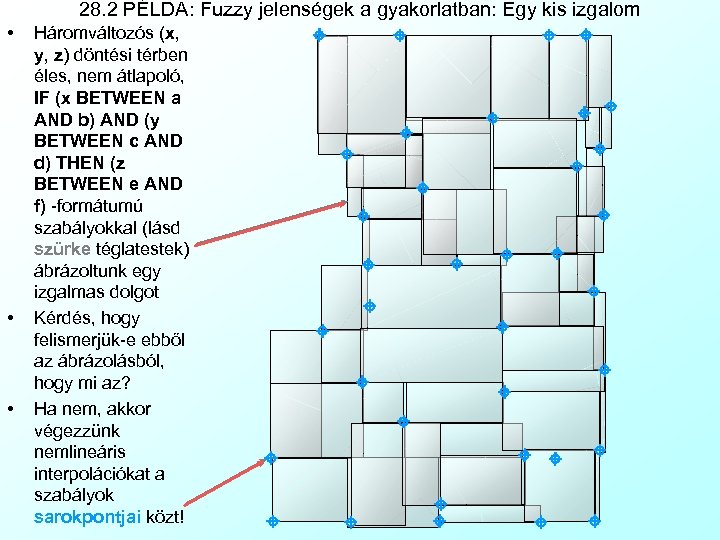28. 2 PÉLDA: Fuzzy jelenségek a gyakorlatban: Egy kis izgalom • • • Háromváltozós (x, y, z) döntési térben éles, nem átlapoló, IF (x BETWEEN a AND b) AND (y BETWEEN c AND d) THEN (z BETWEEN e AND f) -formátumú szabályokkal (lásd szürke téglatestek) ábrázoltunk egy izgalmas dolgot Kérdés, hogy felismerjük-e ebből az ábrázolásból, hogy mi az? Ha nem, akkor végezzünk nemlineáris interpolációkat a szabályok sarokpontjai közt!

• 28. 2 PÉLDA: Fuzzy jelenségek a gyakorlatban: Egy kis izgalom Így egy ismerős hiperfelületet kapunk: A két példából láthattuk, hogy: • A szabályok életlen, átlapoló definiálása (pl. mikor a pixeleket összemosva, messziről láttuk), • Illetve a köztük lévő nem lineáris interpoláció (pl. összemosás, vagy a női test „végigsimítása”) • Hatékonyabban ábrázolhat komplex nemlineáris, nem monoton, nem folytonos vezérlési függvényeket

A Fuzzy Rendszerek alapfogalmai 2 • Fuzzy logika (Fuzzy Logic): [0, 1] folytonos intervallumban mért igazságértékeket (0: hamis, 1: igaz) használó többértékű logika (Multivalued Logic), a klasszikus kétértékű {0, 1} Boole-féle logika kiterjesztése Fuzzy rendszerek összehasonlítása az éles szabályalapú rendszerekkel, előnyök: • A szabályalapú rendszerekhez hasonlóan - ellentétben az analitikus módszerekkel - elősegíti a gyors prototipus fejlesztést, mert a szabálybázis moduláris, könnyen bővíthető, ha a rendszer bonyolódik. • A fuzzy logika, az átlapoló szabályok és a nemlineáris interpoláció használatából eredő rugalmassága miatt jóval kevesebb szabályt igényel adott probléma megoldására, mint az éles szabályalapú rendszerek • Következtetési mechanizmusa nagyságrendekkel egyszerűbb és gyorsabb, mert a fuzzy logika többértékűsége és a fuzzy szabályok átlapoló volta miatt alapból lekezeli az önellentmondásokat, nem kellenek ezek ellenőrzésére, feloldására külön segéd-algoritmusok. Nem követeli meg, hogy a szakértőktől begyűjtött szabálybázis 100% -ig konzisztens legyen, ami sok alkalmazási területen (pl. orvoslás, tőzsde) irreális követelmény.

A Fuzzy Rendszerek alapfogalmai 3 • A szimbolikus tudásábrázolást használó szabályalapú rendszerekkel ellentétben, jól kezel folytonos döntési változókat is, és ezek közt bonyolult nemlineáris összefüggéseket tud úgy modellezni, hogy közben nincs szükség bonyolult, számolásigényes lebegőpontos műveletekre (mint pl. zárt formulával meg nem adható eloszlásfüggvények közelítése, stb. ) • Így alacsonyak a hardverrel szembeni követelményei memóriaigény és számítási idő tekintetében, ezért tipikusan jól használható olcsó, egyszerű mikrokontrollerekben (Microcontroller) (ipari folyamatvezérlő mikroprocesszorokban) is • A fuzzy szabályokat szöveges nyelvi eszközökkel is meg tudja jeleníteni, amelyek közelebb állnak a természetes emberi nyelvhez, mint az éles szabályalapú rendszerek 100%-os logikai konzisztenciát követelő HA-AKKOR szabályai. Ezért a látens szakértői tudást, intuíciókat könnyebb fuzzy szabályok formájában megfogalmazni • Belső működése (Throughput) a szöveges nyelvi megjelenítés miatt jobban átlátható, mint az analitikus módszereké • Speciális alkalmazásokban (pl. tőzsdei árfolyam előrejelzés) – ellentétben a klasszikus sokváltozós statisztikai módszerek pontvagy intervallum-becsléseivel - többértékű eredményt is szolgáltat, ami elősegíti az alternatívákban történő tervezést

A Fuzzy Rendszerek alapfogalmai 4 A fuzzy rendszerek fő hátrányai a következőkben foglalhatók össze: • A szöveges nyelvi szabályok összeállítása manuálisan történik, bár támogatható mesterséges neurális hálózatok (Artificial Neural Networks) tanulásával • A manuális szabályszerkesztés miatt inkább kevesebb változó közti bonyolultabb nemlineáris kapcsolat modellezésére alkalmas, magas változószámnál nehézkes a használata • Akkor tesztelhető csak jól, ha a vezérelni, vagy előrejelezni kívánt rendszernek megvan a fizikai reprezentációja, vagy analitikus úton szimulálható a működése, és csupán a vezérlését nehézkes analitikusan optimalizálni. Nem jól használható, ha a szimuláció sem fizikailag, sem analitikusan nem áll rendelkezésre Története: • 1965 Lotfi Zadeh, Berkeley, USA: kitalálja a fuzzy logikát • 1970 Ebrahim Mamdani, UK: 1. ipari alkalmazás gőzturbina szabályzó • 1980 s Japán alkalmazások: a gyors prototipizálás és egyszerűen érthető throughput illeszkedik a japán menedzsment módszerekhez – 1983 Fuji Electric: szennyvíztisztító vezérlés – 1987 Hitachi: metró vezérlés – 1990 Sony: videókamera képremegés-stabilizátor – 199: Toyota: Autó gyújtás vezérlés • 1990 -es évek Hans Jürgen Zimmermann: EU-ban is beindul az ipari automatizálás • 1995 -től megjelennek PC-re ez első Fuzzy rendszer tervező shellek, felmerül a kombinálás lehetősége neurális hálózatokkal • 2000 -re sztenderd ipari folyamatvezérlési technlógiává válik

A Fuzzy Rendszerek alapfogalmai 4 A bizonytalanság ideáltípusai (Types of Uncertainty): • Sztochasztikus (Stochastic): – Pl. 80%, hogy „a MOL részvény heti záró árfolyama 2100 és 2260 Ft közt lesz a jövő héten”. – Pontosan definiált események bizonytalan bekövetkezése, – A “MOL”, “részvény”, “hét”, “árfolyam”, “záró”, “Ft” fogalmak pontos szabályok által definiáltak – A valószínűségszámítás kezeli: intervallumbecslésekkel és statisztikai próbákkal • Lexikális (Lexical): – Pl. „X magas ember”. – Életlenül definiált, de bizonyosan bekövetkező események: – Ki a magas? Nehéz éles szabályt adni: 180 cm felett tökéletesen az? 179 cm-el meg egyáltalán nem magas? Kikhez képest magas: gyerekek, nők, pigmeusok, kosárlabdázók? Mindig a problémakörnyezet dönt. – A fuzzy logika kezeli: minden magassághoz egy [0, 1] folytonos intervallumban mért igazságértékeket rendel, aszerint hogy a problémakörnyezetben mennyire jellemző rá a „magas” fogalom • A gyakorlatban a kettő keveredik: – pl. „Valószínűleg sikeres pénzügyi évünk lesz az idén” – Mi a sikeres pénzügyi év (a csőd elkerülése vagy betörés a kínai piacra)? – Ez lexikális bizonytalanság – Mennyi az esélye a bekövetkezésének? – Ez bekövetkezési bizonytalanság

Az előadás tartalma A Fuzzy Rendszerek alapfogalmai • 28. 1 PÉLDA: Fuzzy jelenségek a gyakorlatban: Mit ábrázol a kép? • 28. 2 PÉLDA: Fuzzy jelenségek a gyakorlatban: Egy kis izgalom • Fuzzy logika • A Fuzzy rendszerek előnyei és hátrányai • A Fuzzy rendszerek története • A bizonytalanság ideáltípusai A Fuzzy Rendszerek alkotóelemei • A Fuzzy halmaz • A tagságfüggvény fajtái • A fuzzy nyelvi változó Fuzzy nyelvi változók kreációja • Egyenlő intervallumok módszere • Parciális gyakorisági hisztogrammok módszere • Klasztercentrumok módszere • Átlapolás • A tagságfüggvények fajtájának kiválasztása • Speciális tagságfüggvényű szélső fuzzy értékek használata Fuzzy szabályok • Feltételi rész • Fuzzy szabálysúly • Következtetési rész Fuzzy következtetési mechanizmus • Kompozíciós módszerek • Dekompozíciós módszerek • Példa a vezérlési függvény modellezésére

A Fuzzy Rendszerek alkotóelemei 1 F Fuzzy halmaz, Fuzzy érték (Fuzzy set, Fuzzy Value): • Egy életlenül definiált (Non-crisp) (de nem pontatlanul!), szöveges címkével (Fuzzy Linguistic Value) ellátott érték (pl. „Magas láz”): • Adott X értelmezési tartományon (Universe), (pl. celsius skála) felvett x X folytonos vagy diszkrét, bármely skálán mért alapváltozó (base variable), (pl. testhőmérséklet, C°) értékeihez • m. F(x) tagságfüggvényt (MBF, membership function) definál, amelynek értékkészlete a [0, 1] tartományba esik, (pl. emelkedő Sgörbe +37 C° -os inflexiós ponttal) • Ahol 0 jelenti, hogy az alapváltozó adott értékénél egyáltalán nem jellemző, 1 hogy teljesen jellemző a fuzzy érték jelenléte (pl. 0: abszolút nem lázas, 1: abszolút lázas) „Magas láz” • A magas láznak az orvosi gyakor- m(Testhőmérséklet) latban nincs éles C° definíciója, függ a páciens egyébb tüneteitől, (pl. izzadás, remegés), így egy komplex jelenségnek tekinthető. Testhőmérséklet +33 C +37 C +41 C

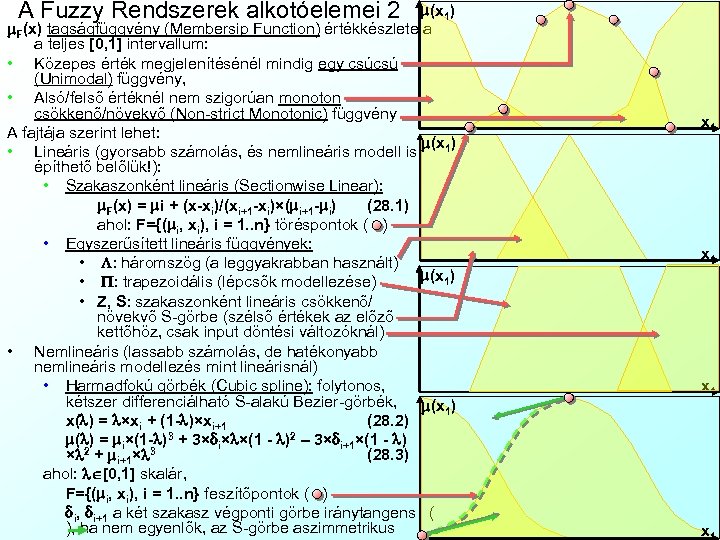A Fuzzy Rendszerek alkotóelemei 2 m(x 1) m. F(x) tagságfüggvény (Membersip Function) értékkészlete a a teljes [0, 1] intervallum: • Közepes érték megjelenítésénél mindig egy csúcsú (Unimodal) függvény, • Alsó/felső értéknél nem szigorúan monoton csökkenő/növekvő (Non-strict Monotonic) függvény A fajtája szerint lehet: m(x 1) • Lineáris (gyorsabb számolás, és nemlineáris modell is építhető belőlük!): • Szakaszonként lineáris (Sectionwise Linear): m. F(x) = mi + (x-xi)/(xi+1 -xi)×(mi+1 -mi) (28. 1) ahol: F={(mi, xi), i = 1. . n} töréspontok ( ) • Egyszerűsített lineáris függvények: • L: háromszög (a leggyakrabban használt) m(x 1) • P: trapezoidális (lépcsők modellezése) • Z, S: szakaszonként lineáris csökkenő/ növekvő S-görbe (szélső értékek az előző kettőhöz, csak input döntési változóknál) • Nemlineáris (lassabb számolás, de hatékonyabb nemlineáris modellezés mint lineárisnál) • Harmadfokú görbék (Cubic spline): folytonos, kétszer differenciálható S-alakú Bezier-görbék, m(x 1) x(l) = l×xi + (1 -l)×xi+1 (28. 2) m(l) = mi×(1 -l)3 + 3×di×l×(1 - l)2 – 3×di+1×(1 - l) ×l 2 + mi+1×l 3 (28. 3) ahol: l [0, 1] skalár, F={(mi, xi), i = 1. . n} feszítőpontok ( ) di, di+1 a két szakasz végponti görbe iránytangens ( ), ha nem egyenlők, az S-görbe aszimmetrikus x 1 x 1

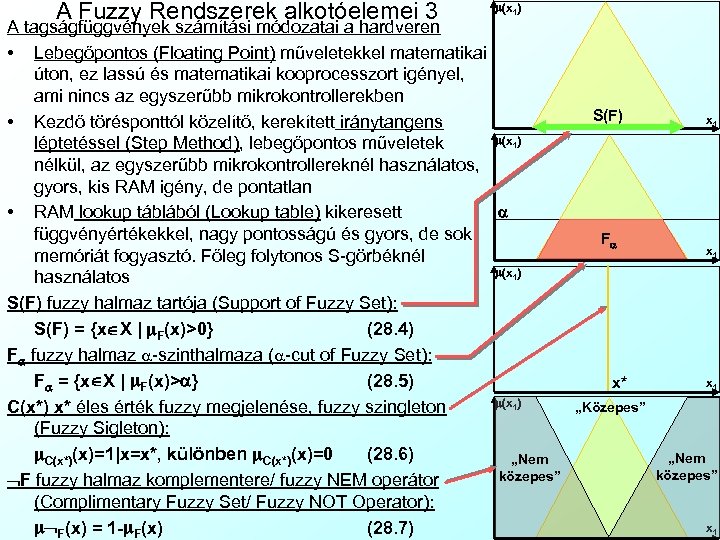A Fuzzy Rendszerek alkotóelemei 3 m(x 1) A tagságfüggvények számítási módozatai a hardveren • Lebegőpontos (Floating Point) műveletekkel matematikai úton, ez lassú és matematikai kooprocesszort igényel, ami nincs az egyszerűbb mikrokontrollerekben • Kezdő törésponttól közelítő, kerekített iránytangens m(x 1) léptetéssel (Step Method), lebegőpontos műveletek nélkül, az egyszerűbb mikrokontrollereknél használatos, gyors, kis RAM igény, de pontatlan a • RAM lookup táblából (Lookup table) kikeresett függvényértékekkel, nagy pontosságú és gyors, de sok memóriát fogyasztó. Főleg folytonos S-görbéknél m(x 1) használatos S(F) fuzzy halmaz tartója (Support of Fuzzy Set): S(F) = {x X | m. F(x)>0} (28. 4) Fa fuzzy halmaz a-szinthalmaza (a-cut of Fuzzy Set): Fa = {x X | m. F(x)>a} (28. 5) m(x 1) C(x*) x* éles érték fuzzy megjelenése, fuzzy szingleton (Fuzzy Sigleton): m. C(x*)(x)=1|x=x*, különben m. C(x*)(x)=0 (28. 6) „Nem közepes” F fuzzy halmaz komplementere/ fuzzy NEM operátor (Complimentary Fuzzy Set/ Fuzzy NOT Operator): m F(x) = 1 -m. F(x) (28. 7) S(F) Fa x* x 1 x 1 „Közepes” „Nem közepes” x 1

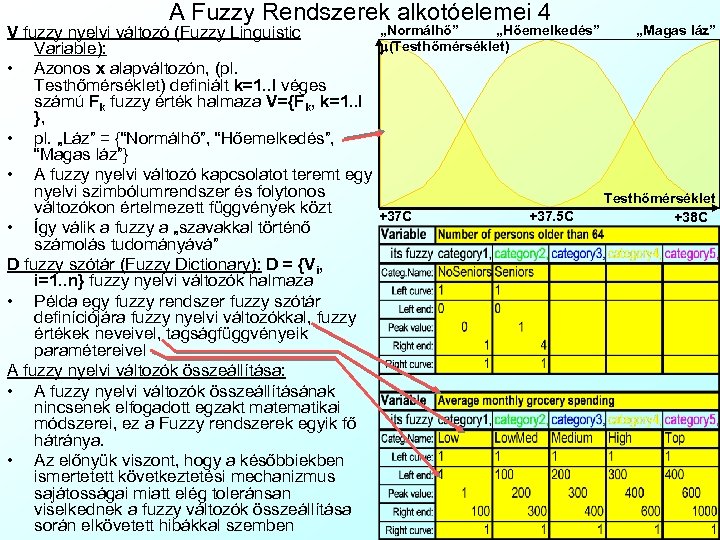A Fuzzy Rendszerek alkotóelemei 4 „Normálhő” „Magas láz” „Hőemelkedés” V fuzzy nyelvi változó (Fuzzy Linguistic m(Testhőmérséklet) Variable): • Azonos x alapváltozón, (pl. Testhőmérséklet) definiált k=1. . l véges számú Fk fuzzy érték halmaza V={Fk, k=1. . l }, • pl. „Láz” = {“Normálhő”, “Hőemelkedés”, “Magas láz”} • A fuzzy nyelvi változó kapcsolatot teremt egy nyelvi szimbólumrendszer és folytonos Testhőmérséklet változókon értelmezett függvények közt +37 C +37. 5 C +38 C • Így válik a fuzzy a „szavakkal történő számolás tudományává” D fuzzy szótár (Fuzzy Dictionary): D = {Vi, i=1. . n} fuzzy nyelvi változók halmaza • Példa egy fuzzy rendszer fuzzy szótár definíciójára fuzzy nyelvi változókkal, fuzzy értékek neveivel, tagságfüggvényeik paramétereivel A fuzzy nyelvi változók összeállítása: • A fuzzy nyelvi változók összeállításának nincsenek elfogadott egzakt matematikai módszerei, ez a Fuzzy rendszerek egyik fő hátránya. • Az előnyük viszont, hogy a későbbiekben ismertetett következtetési mechanizmus sajátosságai miatt elég toleránsan viselkednek a fuzzy változók összeállítása során elkövetett hibákkal szemben

Az előadás tartalma A Fuzzy Rendszerek alapfogalmai • 28. 1 PÉLDA: Fuzzy jelenségek a gyakorlatban: Mit ábrázol a kép? • 28. 2 PÉLDA: Fuzzy jelenségek a gyakorlatban: Egy kis izgalom • Fuzzy logika • A Fuzzy rendszerek előnyei és hátrányai • A Fuzzy rendszerek története • A bizonytalanság ideáltípusai A Fuzzy Rendszerek alkotóelemei • A Fuzzy halmaz • A tagságfüggvény fajtái • A fuzzy nyelvi változó Fuzzy nyelvi változók kreációja • Egyenlő intervallumok módszere • Parciális gyakorisági hisztogrammok módszere • Klasztercentrumok módszere • Átlapolás • A tagságfüggvények fajtájának kiválasztása • Speciális tagságfüggvényű szélső fuzzy értékek használata Fuzzy szabályok • Feltételi rész • Fuzzy szabálysúly • Következtetési rész Fuzzy következtetési mechanizmus • Kompozíciós módszerek • Dekompozíciós módszerek • Példa a vezérlési függvény modellezésére

• Pl. a Lesson 26 -ban szereplő Naugatuck Framed Seat Inc. A fuzzy értékek számának és csúcsaik helyzetének példában a mérnökök korábbi meghatározása: tapasztalataik alapján sejtk, hogy • Az itt elkövetett hibák iránt a legkevésbé toleránsak a parabolikus kapcsolat van a fuzzy rendszerek, ezért többféle módszer is rendelkezésre gyerekülés mérete és áll: használhatósága közt: van egy Egyenlő intervallumok módszere (Equal Intervals Method): közepes méret, ami a legjobb • Alkalmazásához csak azt kell tudni, hogy mi az • A parabola majdani modellezésére alapváltozó gyakorlatban előforduló (min, max) elég egy 3 értékű fuzzy nyelvi értéktartománya, illetve, hogy az adott alapváltozó szerint változót felvenni: Méret = {„Kicsi”, hányadfokú parciális hatást várunk a vezérlési „Közepes”, „Nagy”} függvényben. • Hüvelykujjszabályként (Rules of Thumb) mindig eggyel több értéket alkalmazunk, mint ahányad fokú kapcsolatot várunk (pl. másodfokúnál hármat, negyedfokúnál ötöt, stb. ), ezek egyenlő intervallumokra osztják az alapváltozó értéktartományát. • A módszer előnye, hogy nem kellenek hozzá az input/output változók múltbeli megfigyelései, így prototipizáláskor gyorsan ad egy olyan kiindulási alapot, m(x 1) ami később még finomítható a vezérlés szimulációja során. „Kicsi” „Közepes” „Nagy” • Hátránya, hogy a kezdeti beállítás sokszor nagyon messze van az optimálistól. Ezen úgy segíthetünk, hogy ha pl. multiplikatív parciális hatást sejtünk, akkor nem egyenlő intervallumokban vesszük fel az értékeket, hanem úgy Méret, inch hogy tartóik egy növekvő vagy csökkenő mértani sorozatot m(x 1) alkossanak • Ha még a parciális hatás várható fokszámát sem tudjuk, akkor általában páratlan számú, 5, 7 vagy 9 darab értéket veszünk fel, ami illeszkedik az emberi Rövid Távú Memória (lásd: Session 1 ) méretéhez. Ez megkönnyíti később a fuzzy szabályok megalkotását. A Fuzzy nyelvi változók kreációja 1 x 1

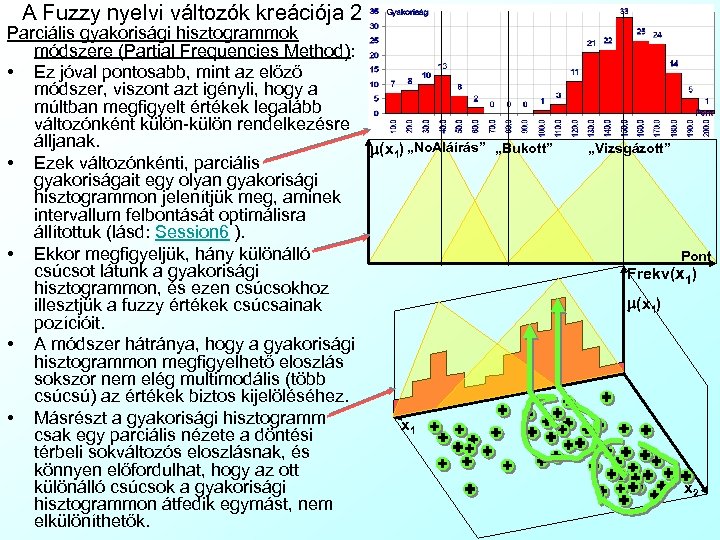A Fuzzy nyelvi változók kreációja 2 Parciális gyakorisági hisztogrammok módszere (Partial Frequencies Method): • Ez jóval pontosabb, mint az előző módszer, viszont azt igényli, hogy a múltban megfigyelt értékek legalább változónként külön-külön rendelkezésre álljanak. m(x 1) „No. Aláírás” • Ezek változónkénti, parciális gyakoriságait egy olyan gyakorisági hisztogrammon jelenítjük meg, aminek intervallum felbontását optimálisra állítottuk (lásd: Session 6 ). • Ekkor megfigyeljük, hány különálló csúcsot látunk a gyakorisági hisztogrammon, és ezen csúcsokhoz illesztjük a fuzzy értékek csúcsainak pozícióit. • A módszer hátránya, hogy a gyakorisági hisztogrammon megfigyelhető eloszlás sokszor nem elég multimodális (több csúcsú) az értékek biztos kijelöléséhez. • Másrészt a gyakorisági hisztogramm x 1 csak egy parciális nézete a döntési térbeli sokváltozós eloszlásnak, és könnyen előfordulhat, hogy az ott különálló csúcsok a gyakorisági hisztogrammon átfedik egymást, nem elkülöníthetők. „Bukott” „Vizsgázott” Pont Frekv(x 1) m(x 1) x 2

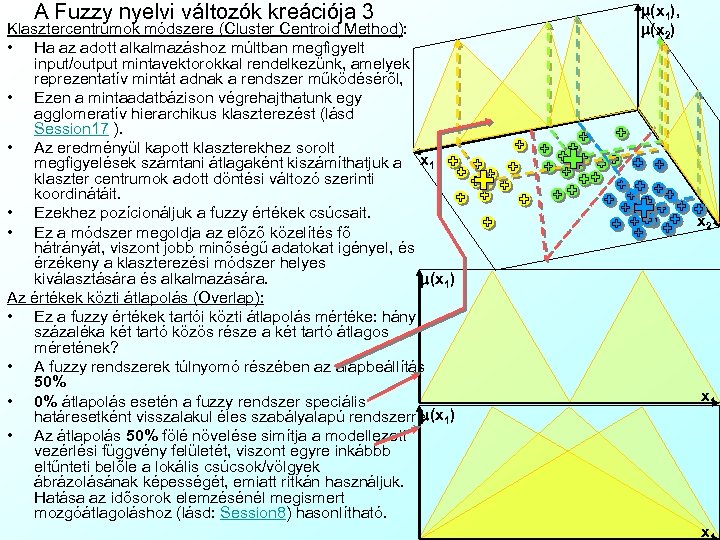A Fuzzy nyelvi változók kreációja 3 Klasztercentrumok módszere (Cluster Centroid Method): • Ha az adott alkalmazáshoz múltban megfigyelt input/output mintavektorokkal rendelkezünk, amelyek reprezentatív mintát adnak a rendszer működéséről, • Ezen a mintaadatbázison végrehajthatunk egy agglomeratív hierarchikus klaszterezést (lásd Session 17 ). • Az eredményül kapott klaszterekhez sorolt megfigyelések számtani átlagaként kiszámíthatjuk a x 1 klaszter centrumok adott döntési változó szerinti koordinátáit. • Ezekhez pozícionáljuk a fuzzy értékek csúcsait. • Ez a módszer megoldja az előző közelítés fő hátrányát, viszont jobb minőségű adatokat igényel, és érzékeny a klaszterezési módszer helyes kiválasztására és alkalmazására. m(x 1) Az értékek közti átlapolás (Overlap): • Ez a fuzzy értékek tartói közti átlapolás mértéke: hány százaléka két tartó közös része a két tartó átlagos méretének? • A fuzzy rendszerek túlnyomó részében az alapbeállítás 50% • 0% átlapolás esetén a fuzzy rendszer speciális m(x határesetként visszalakul éles szabályalapú rendszerré 1) • Az átlapolás 50% fölé növelése simítja a modellezett vezérlési függvény felületét, viszont egyre inkábbb eltűnteti belőle a lokális csúcsok/völgyek ábrázolásának képességét, emiatt ritkán használjuk. Hatása az idősorok elemzésénél megismert mozgóátlagoláshoz (lásd: Session 8) hasonlítható. m(x 1), m(x 2) x 2 x 1 x

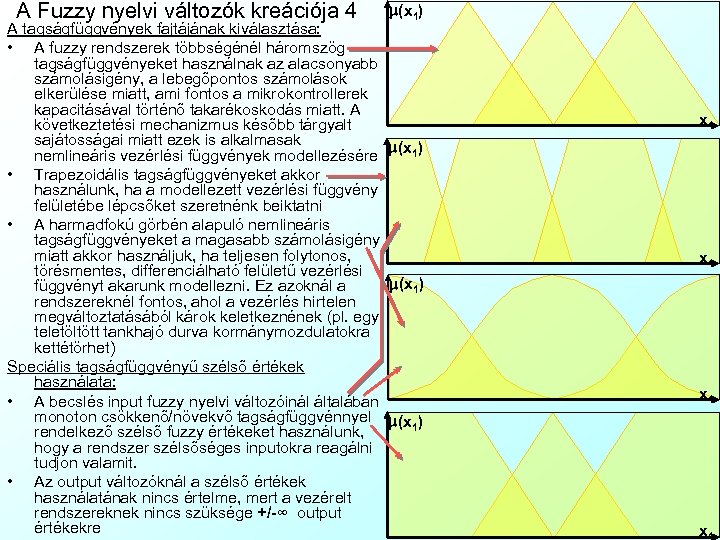A Fuzzy nyelvi változók kreációja 4 m(x 1) A tagságfüggvények fajtájának kiválasztása: • A fuzzy rendszerek többségénél háromszög tagságfüggvényeket használnak az alacsonyabb számolásigény, a lebegőpontos számolások elkerülése miatt, ami fontos a mikrokontrollerek kapacitásával történő takarékoskodás miatt. A következtetési mechanizmus később tárgyalt sajátosságai miatt ezek is alkalmasak nemlineáris vezérlési függvények modellezésére m(x 1) • Trapezoidális tagságfüggvényeket akkor használunk, ha a modellezett vezérlési függvény felületébe lépcsőket szeretnénk beiktatni • A harmadfokú görbén alapuló nemlineáris tagságfüggvényeket a magasabb számolásigény miatt akkor használjuk, ha teljesen folytonos, törésmentes, differenciálható felületű vezérlési m(x 1) függvényt akarunk modellezni. Ez azoknál a rendszereknél fontos, ahol a vezérlés hirtelen megváltoztatásából károk keletkeznének (pl. egy teletöltött tankhajó durva kormánymozdulatokra kettétörhet) Speciális tagságfüggvényű szélső értékek használata: • A becslés input fuzzy nyelvi változóinál általában monoton csökkenő/növekvő tagságfüggvénnyel m(x ) 1 rendelkező szélső fuzzy értékeket használunk, hogy a rendszer szélsőséges inputokra reagálni tudjon valamit. • Az output változóknál a szélső értékek használatának nincs értelme, mert a vezérelt rendszereknek nincs szüksége +/-∞ output értékekre x 1 x 1 x

Az előadás tartalma A Fuzzy Rendszerek alapfogalmai • 28. 1 PÉLDA: Fuzzy jelenségek a gyakorlatban: Mit ábrázol a kép? • 28. 2 PÉLDA: Fuzzy jelenségek a gyakorlatban: Egy kis izgalom • Fuzzy logika • A Fuzzy rendszerek előnyei és hátrányai • A Fuzzy rendszerek története • A bizonytalanság ideáltípusai A Fuzzy Rendszerek alkotóelemei • A Fuzzy halmaz • A tagságfüggvény fajtái • A fuzzy nyelvi változó Fuzzy nyelvi változók kreációja • Egyenlő intervallumok módszere • Parciális gyakorisági hisztogrammok módszere • Klasztercentrumok módszere • Átlapolás • A tagságfüggvények fajtájának kiválasztása • Speciális tagságfüggvényű szélső fuzzy értékek használata Fuzzy szabályok • Feltételi rész • Fuzzy szabálysúly • Következtetési rész Fuzzy következtetési mechanizmus • Kompozíciós módszerek • Dekompozíciós módszerek • Példa a vezérlési függvény modellezésére

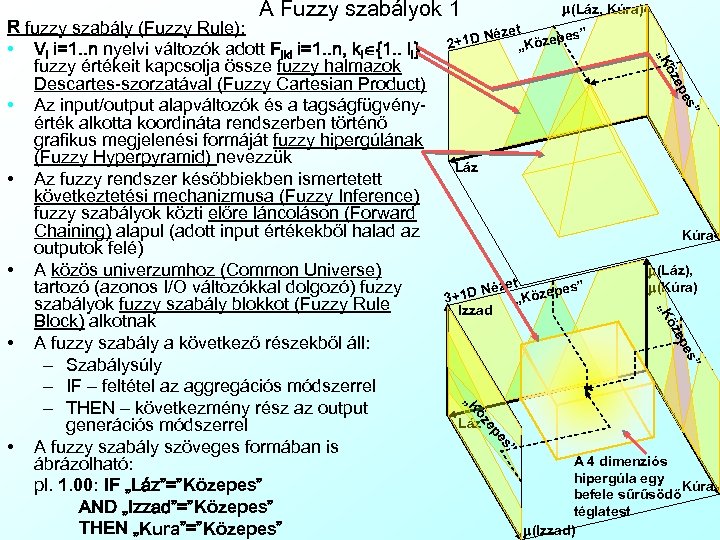A Fuzzy szabályok 1 zet pes” „Köze Né 2+1 D s” e ep öz „K Láz Kúra m(Láz), m(Kúra) öz „K ézet es” 1 D N Közep 3+ „ Izzad ” es ep Láz ” es ep öz „K R fuzzy szabály (Fuzzy Rule): • Vi i=1. . n nyelvi változók adott Fiki i=1. . n, ki {1. . li} fuzzy értékeit kapcsolja össze fuzzy halmazok Descartes-szorzatával (Fuzzy Cartesian Product) • Az input/output alapváltozók és a tagságfügvényérték alkotta koordináta rendszerben történő grafikus megjelenési formáját fuzzy hipergúlának (Fuzzy Hyperpyramid) nevezzük • Az fuzzy rendszer későbbiekben ismertetett következtetési mechanizmusa (Fuzzy Inference) fuzzy szabályok közti előre láncoláson (Forward Chaining) alapul (adott input értékekből halad az outputok felé) • A közös univerzumhoz (Common Universe) tartozó (azonos I/O változókkal dolgozó) fuzzy szabályok fuzzy szabály blokkot (Fuzzy Rule Block) alkotnak • A fuzzy szabály a következő részekből áll: – Szabálysúly – IF – feltétel az aggregációs módszerrel – THEN – következmény rész az output generációs módszerrel • A fuzzy szabály szöveges formában is ábrázolható: pl. 1. 00: IF „Láz”=”Közepes” AND „Izzad”=”Közepes” THEN „Kura”=”Közepes” m(Láz, Kúra) A 4 dimenziós hipergúla egy Kúra befele sűrűsödő téglatest m(Izzad)

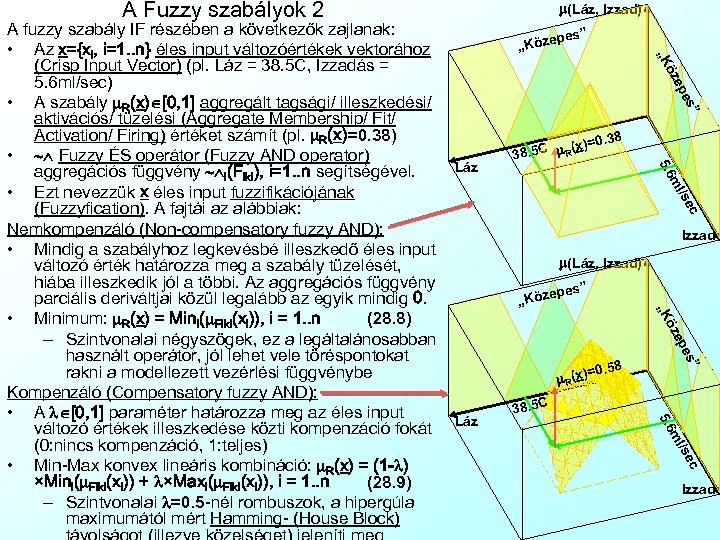A Fuzzy szabályok 2 pes” „Köze s” e ep öz „K . 38 Láz x)=0 8. 5 C m R( 3 c /se ml 5. 6 Izzad m(Láz, Izzad) pes” „Köze öz „K Láz 38. 5 C ” es ep . 58 =0 m R(x) c /se ml 5. 6 A fuzzy szabály IF részében a következők zajlanak: • Az x={xi, i=1. . n} éles input változóértékek vektorához (Crisp Input Vector) (pl. Láz = 38. 5 C, Izzadás = 5. 6 ml/sec) • A szabály m. R(x) [0, 1] aggregált tagsági/ illeszkedési/ aktivációs/ tüzelési (Aggregate Membership/ Fit/ Activation/ Firing) értéket számít (pl. m. R(x)=0. 38) • Fuzzy ÉS operátor (Fuzzy AND operator) aggregációs függvény i(Fiki), i=1. . n segítségével. • Ezt nevezzük x éles input fuzzifikációjának (Fuzzyfication). A fajtái az alábbiak: Nemkompenzáló (Non-compensatory fuzzy AND): • Mindig a szabályhoz legkevésbé illeszkedő éles input változó érték határozza meg a szabály tüzelését, hiába illeszkedik jól a többi. Az aggregációs függvény parciális deriváltjai közül legalább az egyik mindig 0. • Minimum: m. R(x) = Mini(m. Fiki(xi)), i = 1. . n (28. 8) – Szintvonalai négyszögek, ez a legáltalánosabban használt operátor, jól lehet vele töréspontokat rakni a modellezett vezérlési függvénybe Kompenzáló (Compensatory fuzzy AND): • A l [0, 1] paraméter határozza meg az éles input változó értékek illeszkedése közti kompenzáció fokát (0: nincs kompenzáció, 1: teljes) • Min-Max konvex lineáris kombináció: m. R(x) = (1 -l) ×Mini(m. Fiki(xi)) + l×Maxi(m. Fiki(xi)), i = 1. . n (28. 9) – Szintvonalai l=0. 5 -nél rombuszok, a hipergúla maximumától mért Hamming- (House Block) m(Láz, Izzad) Izzad

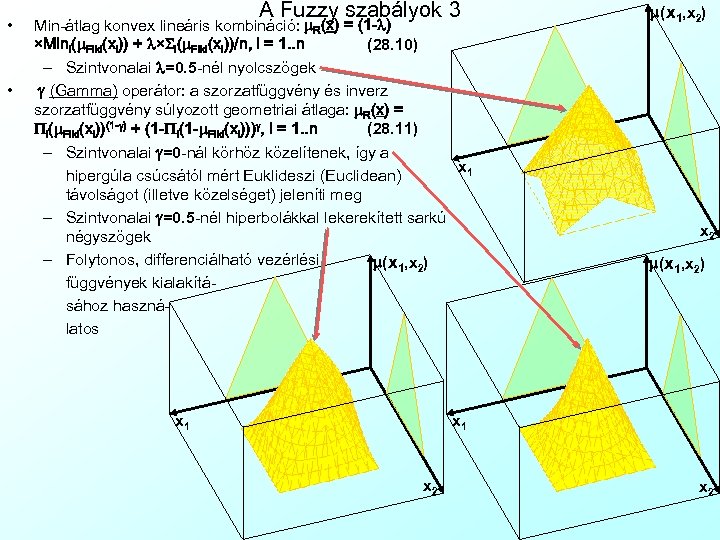• • A Fuzzy szabályok 3 Min-átlag konvex lineáris kombináció: m. R(x) = (1 -l) ×Mini(m. Fiki(xi)) + l×Si(m. Fiki(xi))/n, i = 1. . n (28. 10) – Szintvonalai l=0. 5 -nél nyolcszögek g (Gamma) operátor: a szorzatfüggvény és inverz szorzatfüggvény súlyozott geometriai átlaga: m. R(x) = Pi(m. Fiki(xi))(1 -g) + (1 -Pi(1 -m. Fiki(xi)))g, i = 1. . n (28. 11) – Szintvonalai g=0 -nál körhöz közelítenek, így a x 1 hipergúla csúcsától mért Euklideszi (Euclidean) távolságot (illetve közelséget) jeleníti meg – Szintvonalai g=0. 5 -nél hiperbolákkal lekerekített sarkú négyszögek – Folytonos, differenciálható vezérlési m(x 1, x 2) függvények kialakításához használatos x 1 m(x 1, x 2) x 2 m(x 1, x 2) x 1 x 2

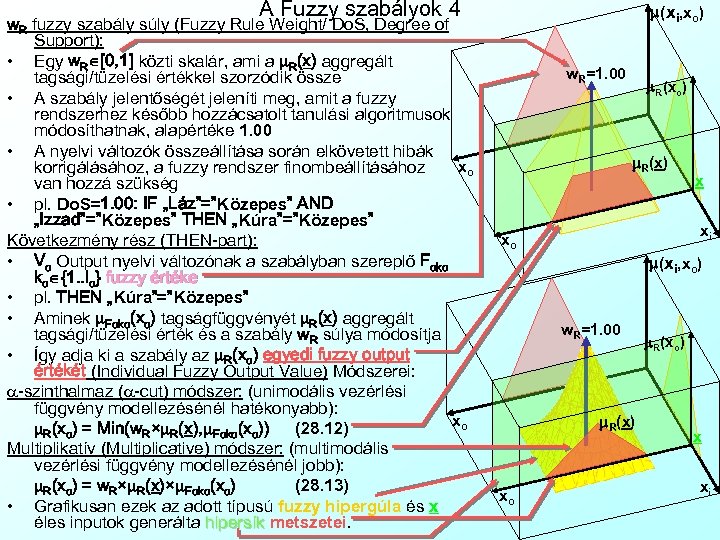A Fuzzy szabályok 4 w. R fuzzy szabály súly (Fuzzy Rule Weight/ Do. S, Degree of Support): • Egy w. R [0, 1] közti skalár, ami a m. R(x) aggregált tagsági/tüzelési értékkel szorzódik össze • A szabály jelentőségét jeleníti meg, amit a fuzzy rendszerhez később hozzácsatolt tanulási algoritmusok módosíthatnak, alapértéke 1. 00 • A nyelvi változók összeállítása során elkövetett hibák xo korrigálásához, a fuzzy rendszer finombeállításához van hozzá szükség • pl. Do. S=1. 00: IF „Láz”=”Közepes” AND „Izzad”=”Közepes” THEN „Kúra”=”Közepes” Következmény rész (THEN-part): • Vo Output nyelvi változónak a szabályban szereplő Foko ko {1. . lo} fuzzy értéke • pl. THEN „Kúra”=”Közepes” • Aminek m. Foko(xo) tagságfüggvényét m. R(x) aggregált tagsági/tüzelési érték és a szabály w. R súlya módosítja • Így adja ki a szabály az m. R(xo) egyedi fuzzy output értékét (Individual Fuzzy Output Value) Módszerei: a-szinthalmaz (a-cut) módszer: (unimodális vezérlési függvény modellezésénél hatékonyabb): xo m. R(xo) = Min(w. R×m. R(x), m. Foko(xo)) (28. 12) Multiplikatív (Multiplicative) módszer: (multimodális vezérlési függvény modellezésénél jobb): m. R(xo) = w. R×m. R(x)×m. Foko(xo) (28. 13) • Grafikusan ezek az adott típusú fuzzy hipergúla és x éles inputok generálta hipersík metszetei. m(xi, xo) w. R=1. 00 m. R(xo) m. R(x) x xi xo m(xi, xo) w. R=1. 00 m. R(x) xo m. R(xo) x xi

Az előadás tartalma A Fuzzy Rendszerek alapfogalmai • 28. 1 PÉLDA: Fuzzy jelenségek a gyakorlatban: Mit ábrázol a kép? • 28. 2 PÉLDA: Fuzzy jelenségek a gyakorlatban: Egy kis izgalom • Fuzzy logika • A Fuzzy rendszerek előnyei és hátrányai • A Fuzzy rendszerek története • A bizonytalanság ideáltípusai A Fuzzy Rendszerek alkotóelemei • A Fuzzy halmaz • A tagságfüggvény fajtái • A fuzzy nyelvi változó Fuzzy nyelvi változók kreációja • Egyenlő intervallumok módszere • Parciális gyakorisági hisztogrammok módszere • Klasztercentrumok módszere • Átlapolás • A tagságfüggvények fajtájának kiválasztása • Speciális tagságfüggvényű szélső fuzzy értékek használata Fuzzy szabályok • Feltételi rész • Fuzzy szabálysúly • Következtetési rész Fuzzy következtetési mechanizmus • Kompozíciós módszerek • Dekompozíciós módszerek • Példa a vezérlési függvény modellezésére

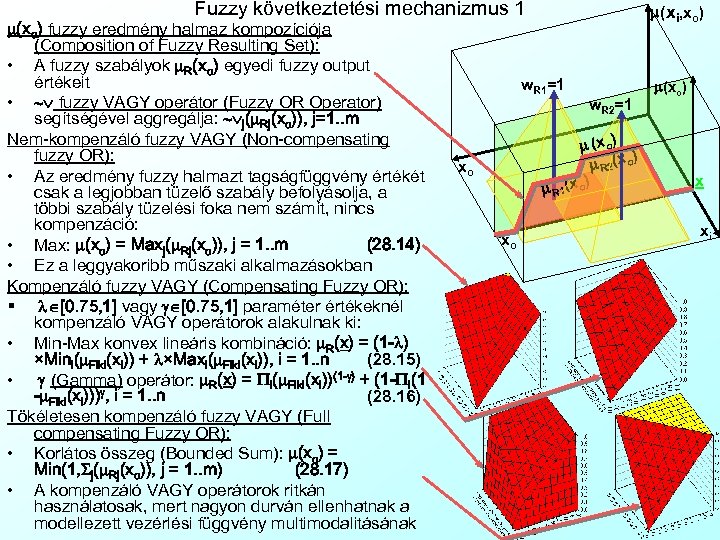Fuzzy következtetési mechanizmus 1 m(xo) fuzzy eredmény halmaz kompozíciója (Composition of Fuzzy Resulting Set): • A fuzzy szabályok m. R(xo) egyedi fuzzy output értékeit • fuzzy VAGY operátor (Fuzzy OR Operator) segítségével aggregálja: j(m. Rj(xo)), j=1. . m Nem-kompenzáló fuzzy VAGY (Non-compensating fuzzy OR): • Az eredmény fuzzy halmazt tagságfüggvény értékét csak a legjobban tüzelő szabály befolyásolja, a többi szabály tüzelési foka nem számít, nincs kompenzáció: • Max: m(xo) = Maxj(m. Rj(xo)), j = 1. . m (28. 14) • Ez a leggyakoribb műszaki alkalmazásokban Kompenzáló fuzzy VAGY (Compensating Fuzzy OR): § l [0. 75, 1] vagy g [0. 75, 1] paraméter értékeknél kompenzáló VAGY operátorok alakulnak ki: • Min-Max konvex lineáris kombináció: m. R(x) = (1 -l) ×Mini(m. Fiki(xi)) + l×Maxi(m. Fiki(xi)), i = 1. . n (28. 15) • g (Gamma) operátor: m. R(x) = Pi(m. Fiki(xi))(1 -g) + (1 -Pi(1 -m. Fiki(xi)))g, i = 1. . n (28. 16) Tökéletesen kompenzáló fuzzy VAGY (Full compensating Fuzzy OR): • Korlátos összeg (Bounded Sum): m(xo) = Min(1, Sj(m. Rj(xo)), j = 1. . m) (28. 17) • A kompenzáló VAGY operátorok ritkán használatosak, mert nagyon durván ellenhatnak a modellezett vezérlési függvény multimodalitásának m(xi, xo) w. R 1=1 w. R 2=1 m (x o) ) m R 2(x o) xo m R 1 xo m(xo) x xi

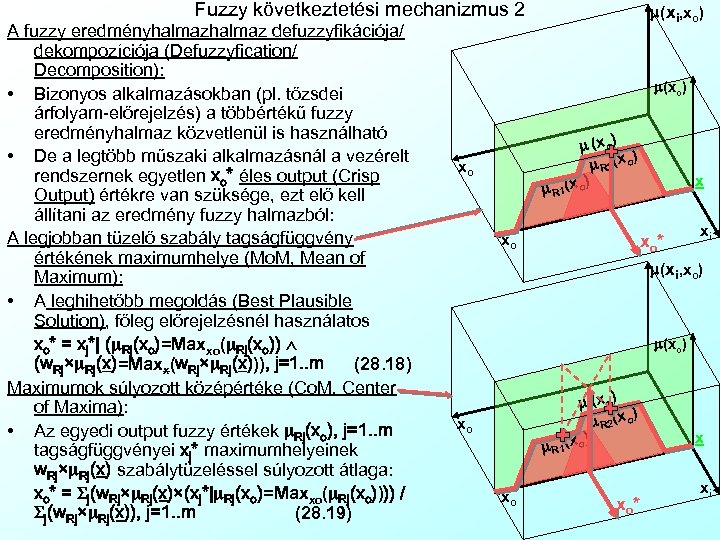Fuzzy következtetési mechanizmus 2 A fuzzy eredményhalmaz defuzzyfikációja/ dekompozíciója (Defuzzyfication/ Decomposition): • Bizonyos alkalmazásokban (pl. tőzsdei árfolyam-előrejelzés) a többértékű fuzzy eredményhalmaz közvetlenül is használható • De a legtöbb műszaki alkalmazásnál a vezérelt rendszernek egyetlen xo* éles output (Crisp Output) értékre van szüksége, ezt elő kell állítani az eredmény fuzzy halmazból: A legjobban tüzelő szabály tagságfüggvény értékének maximumhelye (Mo. M, Mean of Maximum): • A leghihetőbb megoldás (Best Plausible Solution), főleg előrejelzésnél használatos xo* = xj*| (m. Rj(xo)=Maxxo(m. Rj(xo)) (w. Rj×m. Rj(x)=Maxx(w. Rj×m. Rj(x))), j=1. . m (28. 18) Maximumok súlyozott középértéke (Co. M, Center of Maxima): • Az egyedi output fuzzy értékek m. Rj(xo), j=1. . m tagságfüggvényei xj* maximumhelyeinek w. Rj×m. Rj(x) szabálytüzeléssel súlyozott átlaga: xo* = Sj(w. Rj×m. Rj(x)×(xj*|m. Rj(xo)=Maxxo(m. Rj(xo)))) / Sj(w. Rj×m. Rj(x)), j=1. . m (28. 19) m(xi, xo) m(xo) m (x o) ) m R 2(x o) xo x m R 1 xo xo* xi m(xi, xo) m(xo) m (x o) ) m R 2(x o) xo m R 1 xo xo* x xi

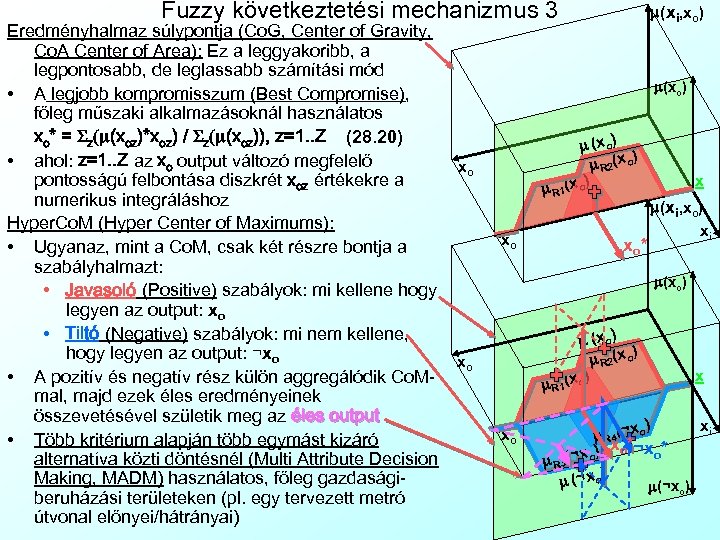Fuzzy következtetési mechanizmus 3 Eredményhalmaz súlypontja (Co. G, Center of Gravity, Co. A Center of Area): Ez a leggyakoribb, a legpontosabb, de leglassabb számítási mód • A legjobb kompromisszum (Best Compromise), főleg műszaki alkalmazásoknál használatos xo* = Sz(m(xoz)*xoz) / Sz(m(xoz)), z=1. . Z (28. 20) • ahol: z=1. . Z az xo output változó megfelelő pontosságú felbontása diszkrét xoz értékekre a numerikus integráláshoz Hyper. Co. M (Hyper Center of Maximums): • Ugyanaz, mint a Co. M, csak két részre bontja a szabályhalmazt: • Javasoló (Positive) szabályok: mi kellene hogy legyen az output: xo • Tiltó (Negative) szabályok: mi nem kellene, hogy legyen az output: ¬xo • A pozitív és negatív rész külön aggregálódik Co. Mmal, majd ezek éles eredményeinek összevetésével születik meg az éles output • Több kritérium alapján több egymást kizáró alternatíva közti döntésnél (Multi Attribute Decision Making, MADM) használatos, főleg gazdaságiberuházási területeken (pl. egy tervezett metró útvonal előnyei/hátrányai) m(xi, xo) m(xo) m (x o) ) m R 2(x o) xo m R 1 xo xo* x m(xi, xo) xi m(xo) m (x o) ) m R 2(x o) xo m R 1 xo x ) xi m R 4(¬x o xo*¬x * o (¬x o) m R 3 ) m (¬ x o m(¬xo)

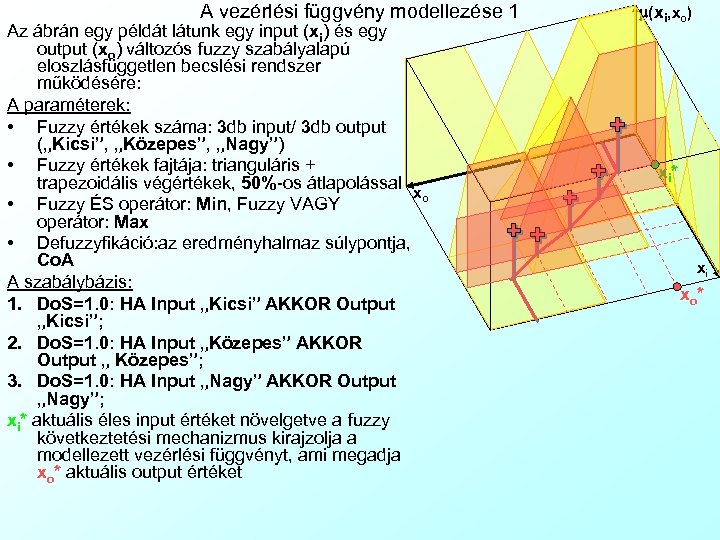A vezérlési függvény modellezése 1 Az ábrán egy példát látunk egy input (xi) és egy output (xo) változós fuzzy szabályalapú eloszlásfüggetlen becslési rendszer működésére: A paraméterek: • Fuzzy értékek száma: 3 db input/ 3 db output („Kicsi”, „Közepes”, „Nagy”) • Fuzzy értékek fajtája: trianguláris + trapezoidális végértékek, 50%-os átlapolással xo • Fuzzy ÉS operátor: Min, Fuzzy VAGY operátor: Max • Defuzzyfikáció: az eredményhalmaz súlypontja, Co. A A szabálybázis: 1. Do. S=1. 0: HA Input „Kicsi” AKKOR Output „Kicsi”; 2. Do. S=1. 0: HA Input „Közepes” AKKOR Output „ Közepes”; 3. Do. S=1. 0: HA Input „Nagy” AKKOR Output „Nagy”; xi* aktuális éles input értéket növelgetve a fuzzy következtetési mechanizmus kirajzolja a modellezett vezérlési függvényt, ami megadja xo* aktuális output értéket m(xi, xo) xi* xi xo*

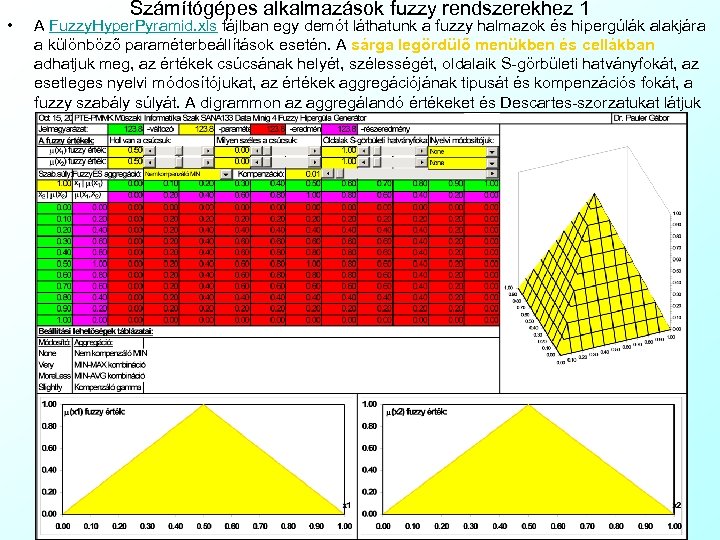• Számítógépes alkalmazások fuzzy rendszerekhez 1 A Fuzzy. Hyper. Pyramid. xls fájlban egy demót láthatunk a fuzzy halmazok és hipergúlák alakjára a különböző paraméterbeállítások esetén. A sárga legördülő menükben és cellákban adhatjuk meg, az értékek csúcsának helyét, szélességét, oldalaik S-görbületi hatványfokát, az esetleges nyelvi módosítójukat, az értékek aggregációjának tipusát és kompenzációs fokát, a fuzzy szabály súlyát. A digrammon az aggregálandó értékeket és Descartes-szorzatukat látjuk

Szakirodalom Fuzzy elméleti alapok: • Fuzzy alapdefiníciók (angolul): http: //en. wikipedia. org/wiki/Fuzzy_logic • Fuzzy bevezető (magyarul): http: //csaba. gamf. hu/segedlet/MI/Johanyak%20 Fuzzy%20 logika%20 segedlet. pdf Kereskedelmi Fuzzy rendszerek: • Informs Gmbh. Fuzzytech: fuzzy szabálygenerátor GUI, időkorlátlan shareware, nincs mentés http: //www. fuzzytech. com • Aptronix Inc. FIDE: 30 napos shareware, GUI: http: //www. aptronix. com/fide/ Ingyenes Fuzzy rendszrek: • Telepítővel és GUI-val rendelkező önálló rendszerek: – XFuzzy: http: //www. imse. cnm. es/Xfuzzy_3. 0/download. html – Fool&Fox (Csak LINUX alól fut!): http: //rhaug. de/fool/ • Fuzzy forráskód könyvtárak – Fuzzy. Clips: C++, Nincs GUI: http: //www. iit. nrc. ca/IR_public/fuzzy. Clips/fuzzy. CLIPSIndex 2. html – Fuzzy. Jess: Java, GUI: http: //www. iit. nrc. ca/IR_public/fuzzy. JToolkit 2. html – j. Fuzzy. Logic: Java, GUI van: http: //jfuzzylogic. sourceforge. net/html/index. html Kereskedelmi adatbányászati rendszerek fuzzy komponensekkel: • Data. Engine Inc. Data. Engine: alapstatisztikák, fuzzy, neurális hálók, általános adatbányászati eszköztár, 30 napos shareware, nincs mentés http: //www. dataengine. de • Attar Inc. XPert. Rule: teljesítménylimitált demó: http: //www. xpertrule. com/index. htm Ingyenes adatbányászati rendszerek fuzzy komponensekkel: • IBM ABLE: http: //www. research. ibm. com/able/doc/reference/overview-summary. html • Yale: http: //www-ai. cs. uni-dortmund. de/SOFTWARE/YALE/documentation. html