6e37b018305bc9d2b0a525dd09dd7078.ppt
- Количество слайдов: 60

PCA and Hebb Rule 0368 -4149 -01 Prof. Nathan Intrator Tuesday 16: 00 -19: 00 Office hours: Wed 4 -5 nin@tau. ac. il cs. tau. ac. il/~nin

Outline l l Goals for neural learning - Unsupervised Goals for statistical/computational learning l l l PCA ICA Exploratory Projection Pursuit Search for non-Gaussian distributions Practical implementations 2

Statistical Approach to Unsupervised Learning l l l Understanding the nature of data variability Modeling the data (sometimes very flexible model) Understanding the nature of the noise Applying prior knowledge Extracting features based on: l l l Prior knowledge Class prediction Unsupervised learning 3
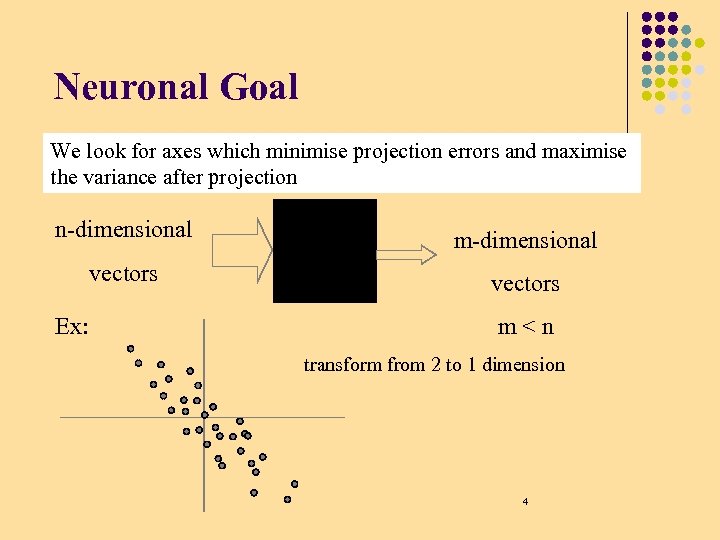
Neuronal Goal We look for axes which minimise projection errors and maximise the variance after projection n-dimensional m-dimensional vectors Ex: m<n transform from 2 to 1 dimension 4
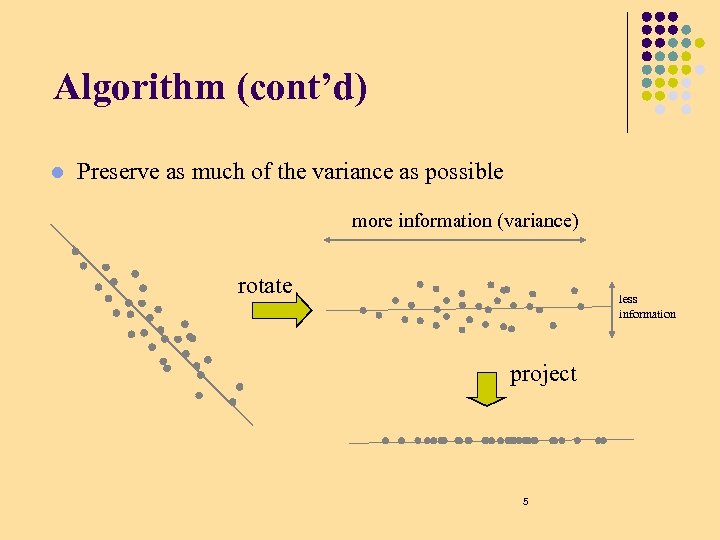
Algorithm (cont’d) l Preserve as much of the variance as possible more information (variance) rotate less information project 5

Linear transformations – example 2 D vectors X in a unit circle with mean (1, 1); Y = A*X, A = 2 x 2 matrix The shape is elongated, rotated and the mean is shifted. 6

Invariant distances Euclidean distance is not invariant to general linear transformations This is invariant only for orthonormal matrices ATA = I that make rigid rotations, without stretching or shrinking distances. Idea: standardize the data in some way to create invariant distances. 7

Data standardization For each vector component X(j)T=(X 1(j), . . . Xd(j)), j=1. . n calculate mean and std: n – number of vectors, d – their dimension Vector of mean feature values. Averages over rows. 8

Standard deviation Calculate standard deviation: Vector of mean feature values. Variance = square of standard deviation (std), sum of all deviations from the mean value. Transform X => Z, standardized data vectors 9

Std data: zero mean and unit variance. Standardize data after making data transformation. Effect: data is invariant to scaling only (diagonal transformation). Distances are invariant, data distribution is the same? ? How to make data invariant to any linear transformations? 10

Terminology (Covariance) l How two dimensions vary from the mean with respect to each other l cov(X, Y) > 0: Dimensions increase together cov(X, Y) < 0: One increases, one decreases l cov(X, Y) = 0: Dimensions are independent l 11

Terminology (Covariance Matrix) l Contains covariance values between all possible dimensions: • Example for three dimensions (x, y, z) (Always symetric): cov(x, x) variance of component x 12

Properties of the Cov matrix l Can be used for creating a distance that is not sensitive to linear transformation l Can be used to find directions which maximize the variance l Determines a Gaussian distribution uniquely (up to a shift) 13

Data standardization example For our example Y=AX, assuming X means=1 and variances = 1 Transformation Vector of mean feature values. Variance check it! How to make this invariant? 14

Covariance matrix Variance (spread around mean value) + correlation between features. CX is d x d where X is d x n dimensional matrix of vectors shifted to their means. Covariance matrix is symmetric Cij = Cji and positive definite. Diagonal elements are variances (square of std), si 2 = Cii Pearson correlation coefficient Spherical distribution of data has Cij=I (unit matrix). Elongated ellipsoids: large off-diagonal elements, strong correlations 15 between features.

Mahalanobis distance Linear combinations of features leads to rotations and scaling of data. Mahalanobis distance: is invariant to linear transformations: 16

Principal components How to avoid correlated features? Correlations covariance matrix is non-diagonal ! Solution: diagonalize it, then use transformation that makes it diagonal to de-correlate features. Z are the eigen vectors of Cx In matrix form, X, Y are dxn, Z, CX, CY are dxd C – symmetric, positive definite matrix XTCX > 0 for ||X||>0; its eigenvectors are orthonormal: its eigenvalues are all non-negative Z – matrix of orthonormal eigenvectors (because Z is real+symmetric), transforms X into Y, with diagonal CY, i. e. decorrelated. 17

Matrix form Eigenproblem for C matrix in matrix form: 18

Principal components PCA: old idea, C. Pearson (1901), H. Hotelling 1933 Z – principal components, of vectors X transformed using eigenvectors of CX Covariance matrix of transformed vectors is diagonal => ellipsoidal distribution of data. Result: PC are linear combinations of all features, providing new uncorrelated features, with diagonal covariance matrix = eigenvalues. Small li small variance data change little in direction Yi PCA minimizes C matrix reconstruction errors: Zi vectors for large li are sufficient to get: because vectors for small eigenvalues will have very small contribution to the covariance matrix. 19
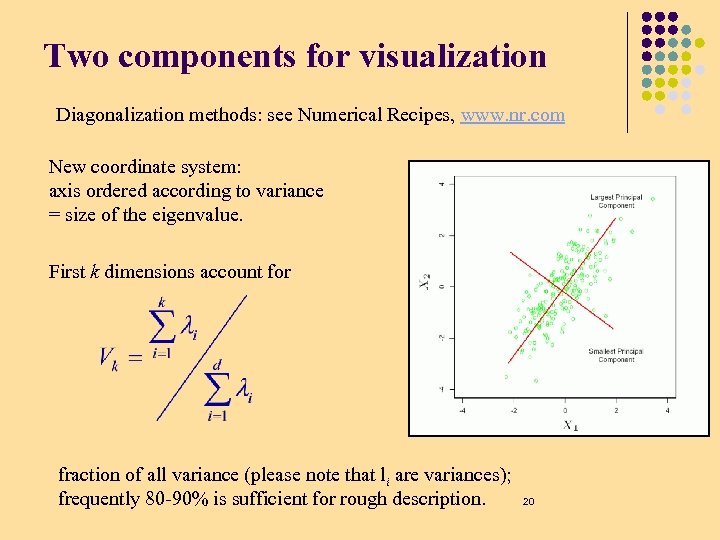
Two components for visualization Diagonalization methods: see Numerical Recipes, www. nr. com New coordinate system: axis ordered according to variance = size of the eigenvalue. First k dimensions account for fraction of all variance (please note that li are variances); frequently 80 -90% is sufficient for rough description. 20

Solving for Eigenvalues & Eigenvectors l Vectors x having same direction as Ax are called eigenvectors of A (A is an n by n matrix). l In the equation Ax= x, is called an eigenvalue of A. l Ax= x (A- I)x=0 l How to calculate x and : l l l Calculate det(A- I), yields a polynomial (degree n) Determine roots to det(A- I)=0, roots are eigenvalues Solve (A- I) x=0 for each to obtain eigenvectors x 21

PCA properties PC Analysis (PCA) may be achieved by: l transformation making covariance matrix diagonal l projecting the data on a line for which the sums of squares of distances from original points to projections is minimal. l orthogonal transformation to new variables that have stationary variances True covariance matrices are usually not known, estimated from data. This works well on single-cluster data; more complex structure may require local PCA, separately for each cluster. PC is useful for: finding new, more informative, uncorrelated features; reducing dimensionality: reject low variance features, reconstructing covariance matrices from low-dim data. 22
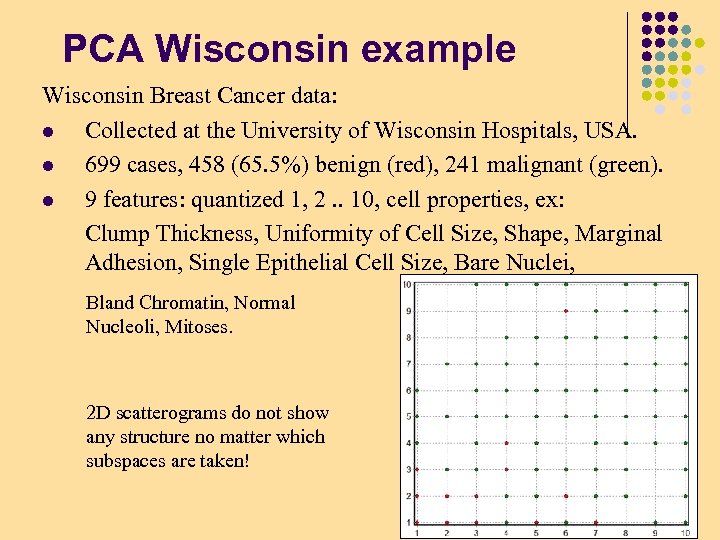
PCA Wisconsin example Wisconsin Breast Cancer data: l Collected at the University of Wisconsin Hospitals, USA. l 699 cases, 458 (65. 5%) benign (red), 241 malignant (green). l 9 features: quantized 1, 2. . 10, cell properties, ex: Clump Thickness, Uniformity of Cell Size, Shape, Marginal Adhesion, Single Epithelial Cell Size, Bare Nuclei, Bland Chromatin, Normal Nucleoli, Mitoses. 2 D scatterograms do not show any structure no matter which subspaces are taken! 23
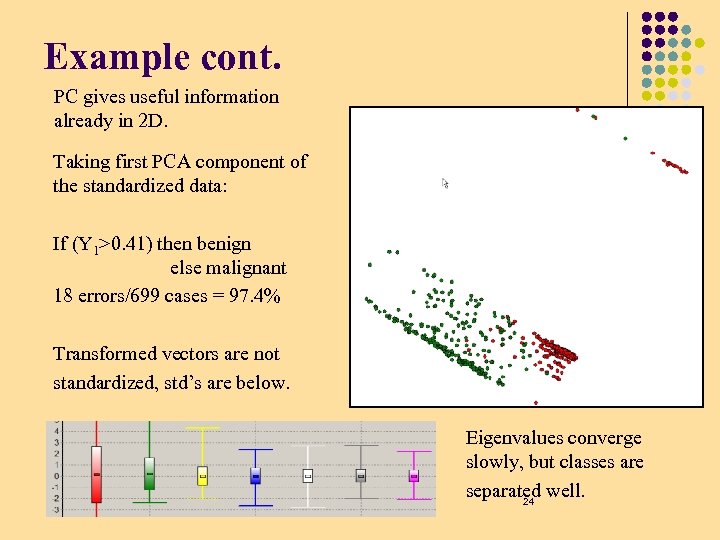
Example cont. PC gives useful information already in 2 D. Taking first PCA component of the standardized data: If (Y 1>0. 41) then benign else malignant 18 errors/699 cases = 97. 4% Transformed vectors are not standardized, std’s are below. Eigenvalues converge slowly, but classes are separated well. 24

PCA disadvantages Useful for dimensionality reduction but: l Largest variance determines which components are used, but does not guarantee interesting viewpoint for clustering data. l The meaning of features is lost when linear combinations are formed. Analysis of coefficients in Z 1 and other important eigenvectors may show which original features are given much weight. PCA may be also done in an efficient way by performing singular value decomposition of the standardized data matrix. PCA is also called Karhuen-Loève transformation. Many variants of PCA are described in A. Webb, Statistical pattern recognition, J. Wiley 2002, good review in Duda and Hart (1973). 25

Exercise (part 1, Updated Mar 10) l How would you calculate efficiently the PCA of data where the dimensionality d is much larger than the number of vector observations n? l Download the Wisconsin Data from the UC Irvine repository, extract PCAs from the data, test scatter plots of original data and after projecting onto the principal components, plot Eigen values 26

Unsupervised learning The Hebb rule – Neurons that fire together wire • together. PCA • RF development with PCA •
Classical Conditioning
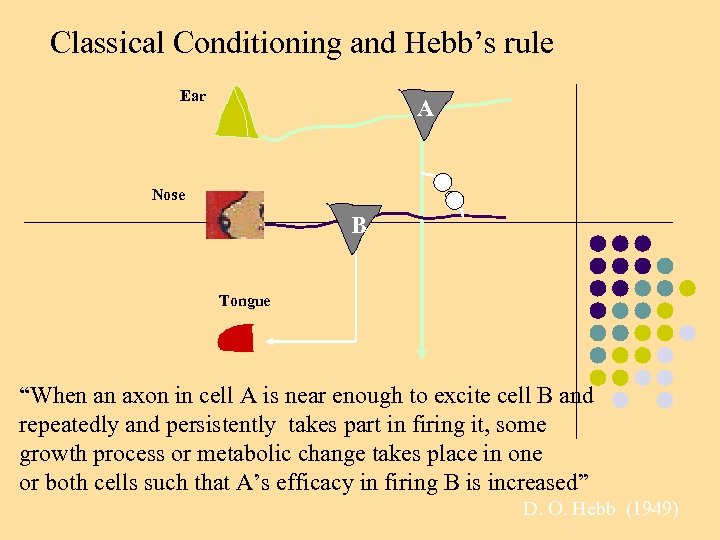
Classical Conditioning and Hebb’s rule Ear A Nose B Tongue “When an axon in cell A is near enough to excite cell B and repeatedly and persistently takes part in firing it, some growth process or metabolic change takes place in one or both cells such that A’s efficacy in firing B is increased” D. O. Hebb (1949)

The generalized Hebb rule: where xi are the inputs and y the output is assumed linear: Results in 2 D
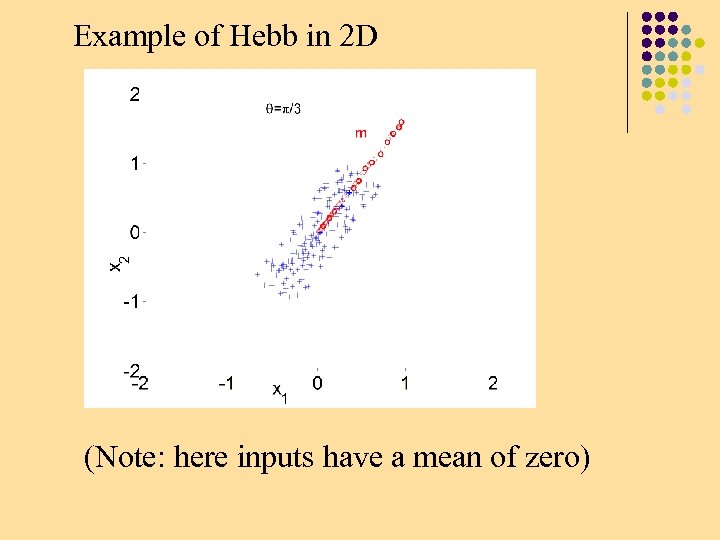
Example of Hebb in 2 D w (Note: here inputs have a mean of zero)

In the simplest case, the change in synaptic weight w is: where x are input vectors and y is the neural response. Assume for simplicity a linear neuron: So we get: Now take an average with respect to the distribution of inputs, get:

If a small change Δw occurs over a short time Δt then: (in matrix notation) If <x>=0 , Q is the covariance function. What is then the solution of this simple first order linear ODE ? (Show on board)

Mathematics of the generalized Hebb rule The change in synaptic weight w is: where x are input vectors and y is the neural response: Assume for simplicity a linear neuron: So we get:

Taking an average of the distribution of inputs And using We obtain and
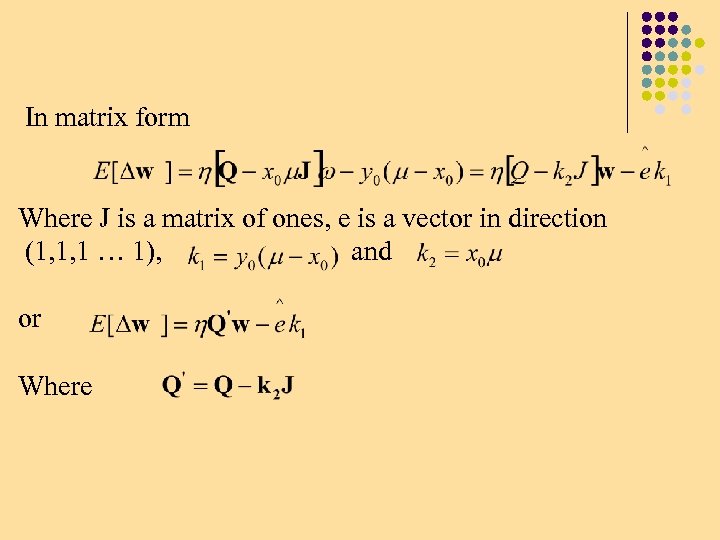
In matrix form Where J is a matrix of ones, e is a vector in direction (1, 1, 1 … 1), and or Where

The equation therefore has the form If k 1 is not zero, this has a fixed point, however it is usually not stable. If k 1=0 then have:

The Hebb rule is unstable – how can it be stabilized while preserving its properties? The stabilized Hebb (Oja) rule. Where: Appoximate to first order in η: Now insert Get: Normalize

} Therefore y The Oja rule therefore has the form:
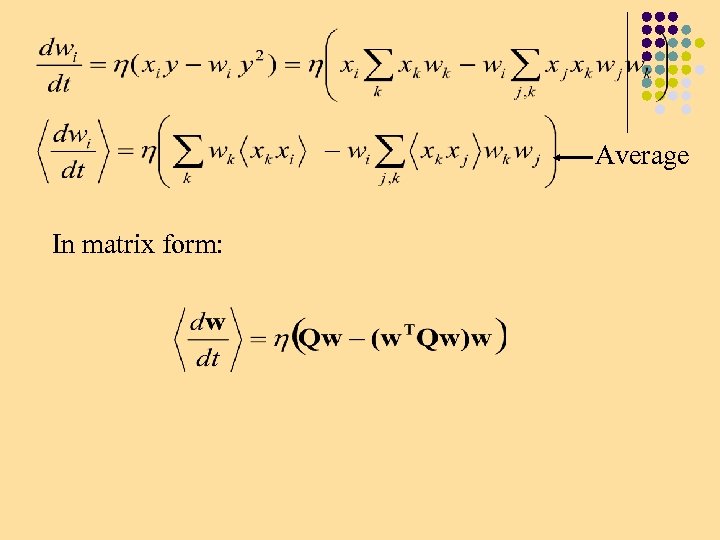
Average In matrix form:

Using this rule the weight vector converges to the eigen-vector of Q with the highest eigen-value. It is often called a principal component or PCA rule. The exact dynamics of the Oja rule have been solved by • Wyatt and Elfaldel 1995 Variants of networks that extract several principal • components have been proposed (e. g: Sanger 1989)
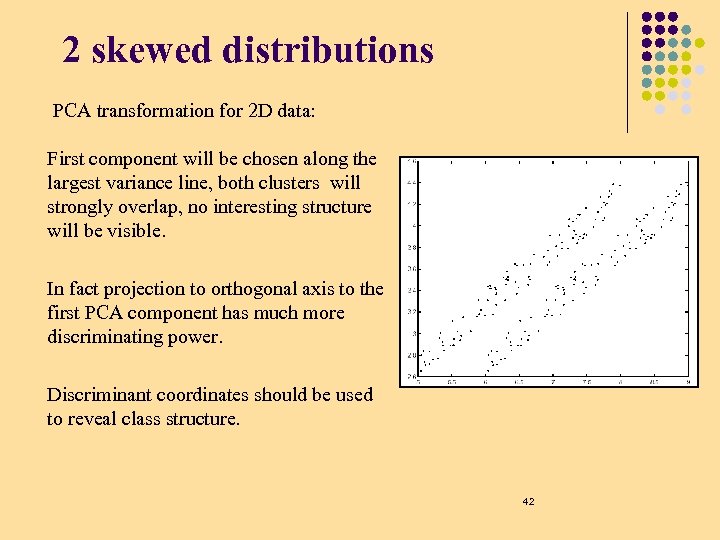
2 skewed distributions PCA transformation for 2 D data: First component will be chosen along the largest variance line, both clusters will strongly overlap, no interesting structure will be visible. In fact projection to orthogonal axis to the first PCA component has much more discriminating power. Discriminant coordinates should be used to reveal class structure. 42

Projection Pursuit 43

Projection Pursuit (PP) PCA and FDA are linear, PP may be linear or non-linear. Find interesting “criterion of fit”, or “figure of merit” function, that allows for low-dim (usually 2 D or 3 D) projection. General transformation with parameters W. Index of “interestingness” Interesting indices may use a priori knowledge about the problem: 1. 2. 3. mean nearest neighbor distance – increase clustering of Y(j) maximize mutual information between classes and features find projection that have non-Gaussian distributions. The last index does not use a priori knowledge; it leads to the Independent Component Analysis (ICA). 44 ICA features are not only uncorrelated, but also independent.

Kurtosis ICA is a special version of PP, recently very popular. Gaussian distributions of variable Y are characterized by 2 parameters: mean value: variance: These are the first 2 moments of distribution; all higher are 0 for G(Y). One simple measure of non-Gaussianity of projections is the 4 -th moment (cumulant) of the distribution, called kurtosis, measures “skewedness” of the distribution. For E{Y}=0 kurtosis is: Super-Gaussian distribution: long tail, peak at zero, k 4(y)>0, like binary image data. sub-Gaussian distribution is more flat and has k 4(y)<0, like speech signal data. 45

Correlation and independence Variables are statistically independent if their joint probability distribution is a product of probabilities for all variables: Features Yi, Yj are uncorrelated if covariance is diagonal, or: Uncorrelated features are orthogonal. Statistically independent features Yi, Yj for any functions give: This is much stronger condition than correlation; in particular the functions may be powers of variables; any non-Gaussian distribution after PCA 46 transformation will still have correlated features.
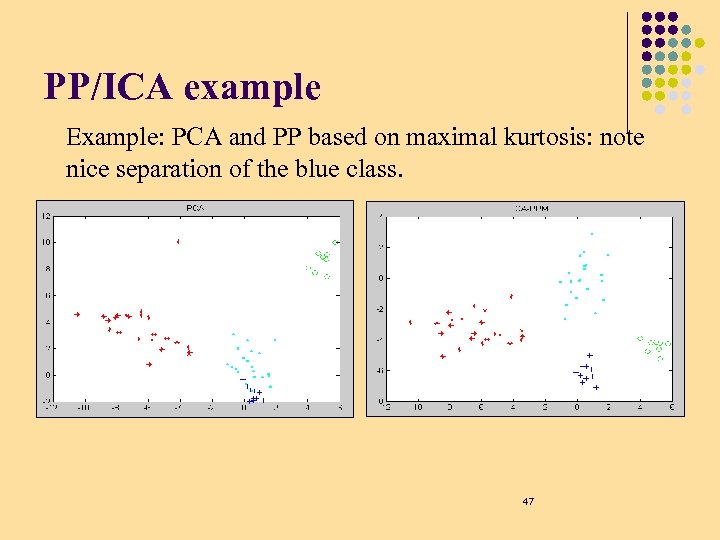
PP/ICA example Example: PCA and PP based on maximal kurtosis: note nice separation of the blue class. 47

Some remarks l l Many formulations of PP and ICA methods exist. PP is used for data visualization and dimensionality reduction. Nonlinear projections are frequently considered, but solutions are more numerically intensive. PCA may also be viewed as PP, max (for standardized data): Index I(Y; W) is based here on maximum variance. Other components are found in the space orthogonal to W 1 T X Same index is used, with projection on space orthogonal to k-1 PCs. 48

How do we find multiple Projections l Statistical approach is complicated: l l l Perform a transformation on the data to eliminate structure in the already found direction Then perform PP again Neural Comp approach: Lateral Inhibition 49
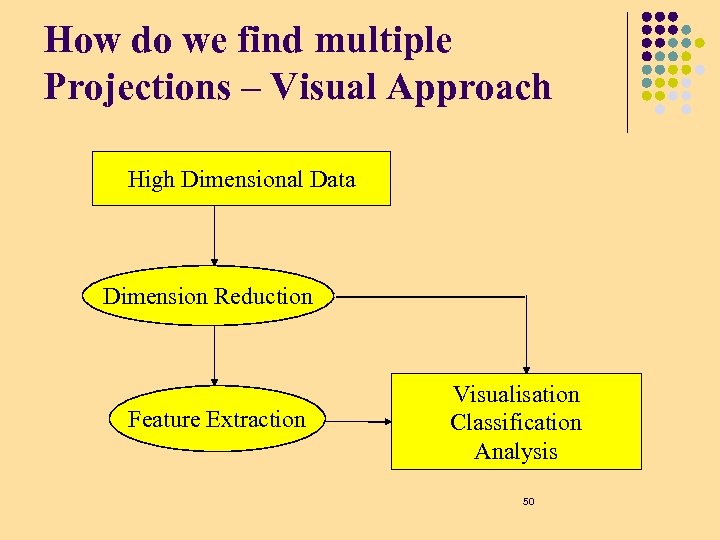
How do we find multiple Projections – Visual Approach High Dimensional Data Dimension Reduction Feature Extraction Visualisation Classification Analysis 50

Projection Pursuit An automated procedure that seeks interesting low dimensional projections of a high dimensional cloud by numerically maximizing an objective function or projection index. Huber, 1985 51

Projection Pursuit is needed l l l Curse of dimensionality Less Robustness worse mean squared error greater computational cost slower convergence to limiting distributions … Required number of labelled samples increases with dimensionality. 52

What is an interesting projection In general: the projection that reveals more information about the structure. In pattern recognition: a projection that maximises class separability in a low dimensional subspace. 53

Projection Pursuit Dimensional Reduction Find lower-dimensional projections of a high-dimensional point cloud to facilitate classification. Exploratory Projection Pursuit Reduce the dimension of the problem to facilitate visualization. 54

Projection Pursuit How many dimensions to use l for visualization l for classification/analysis Which Projection Index to use l measure of variation (Principal Components) l departure from normality (negative entropy) l class separability(distance, Bhattacharyya, Mahalanobis, . . . ) l … 55

Projection Pursuit Which optimization method to choose We are trying to find the global optimum among local ones l l hill climbing methods (simulated annealing) regular optimization routines with random starting points. 56

ICA demos l l ICA has many applications in signal and image analysis. Finding independent signal sources allows for separation of signals from different sources, removal of noise or artifacts. Observations X are a linear mixture W of unknown sources Y Both W and Y are unknown! This is a blind separation problem. How can they be found? If Y are Independent Components and W linear mixing the problem is similar to FDA or PCA, only the criterion function is different. Play with ICALab PCA/ICA Matlab software for signal/image analysis: http: //www. bsp. brain. riken. go. jp/page 7. html 57

ICA demo: images & audio Example from Cichocki’s lab, http: //www. bsp. brain. riken. go. jp/page 7. html X space for images: take intensity of all pixels one vector per image, or take smaller patches (ex: 64 x 64), increasing # vectors l 5 images: originals, mixed, convergence of ICA iterations X space for signals: sample the signal for some time Dt l 10 songs: mixed samples and separated samples 58

Self-organization PCA, FDA, ICA, PP are all inspired by statistics, although some neuralinspired methods have been proposed to find interesting solutions, especially for their non-linear versions. l Brains learn to discover the structure of signals: visual, tactile, olfactory, auditory (speech and sounds). l This is a good example of unsupervised learning: spontaneous development of feature detectors, compressing internal information that is needed to model environmental states (inputs). l Some simple stimuli lead to complex behavioral patterns in animals; brains use specialized microcircuits to derive vital information from signals – for example, amygdala nuclei in rats sensitive to ultrasound signals signifying “cat around”. 59

Models of self-organizaiton SOM or SOFM (Self-Organized Feature Mapping) – self-organizing feature map, one of the simplest models. How can such maps develop spontaneously? Local neural connections: neurons interact strongly with those nearby, but weakly with those that are far (in addition inhibiting some intermediate neurons). History: von der Malsburg and Willshaw (1976), competitive learning, Hebb mechanisms, „Mexican hat” interactions, models of visual systems. Amari (1980) – models of continuous neural tissue. Kohonen (1981) - simplification, no inhibition; leaving two essential factors: competition and cooperation. 60
6e37b018305bc9d2b0a525dd09dd7078.ppt