Pattern-Directed Inference Systems Algorithms and Data Structures II

Pattern-Directed Inference Systems Algorithms and Data Structures II Academic Year 2002 -03

Previous Lectures • (Classical) Problem Solving – Separation of problem space and search engine – Characterization of problem space • Pluggable search engines • Implementations for different search problems, e. g. a subway planning problem

Moving from (Classical) Problem Solvers to Pattern. Directed Inference systems • Operators == rules. • State == database of asserted facts about objects of discourse. • Search engine handles rule-firing.

PDIS • • Assertions, pattern matching and unification Pattern-based retrieval Rules Pattern-Directed Inference Systems (PDIS) in general

Design Methodology • Build simple and stable, then extend module-bymodule – In these lectures, we’ll start with a few very simple systems, and replace them one module at a time. – This is a good design methodology in general. • Write routines at a task level, and hide dependantstructure bookkeeping – BPS program modules highly interdependent (rulesystem/database) – Information must be propagated across consistently – Main routines should hide this propagation

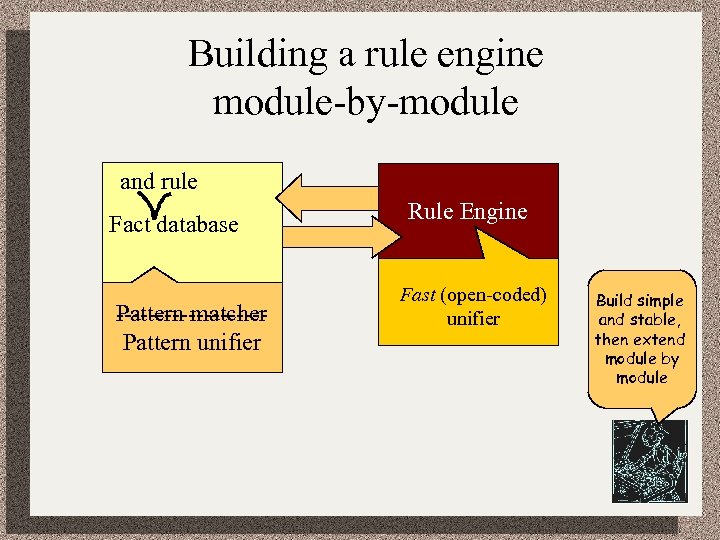Building a rule engine module-by-module and rule Fact database Rule Engine Pattern unifier ---------Pattern matcher Pattern unifier Fast (open-coded) unifier Build simple and stable, then extend module by module

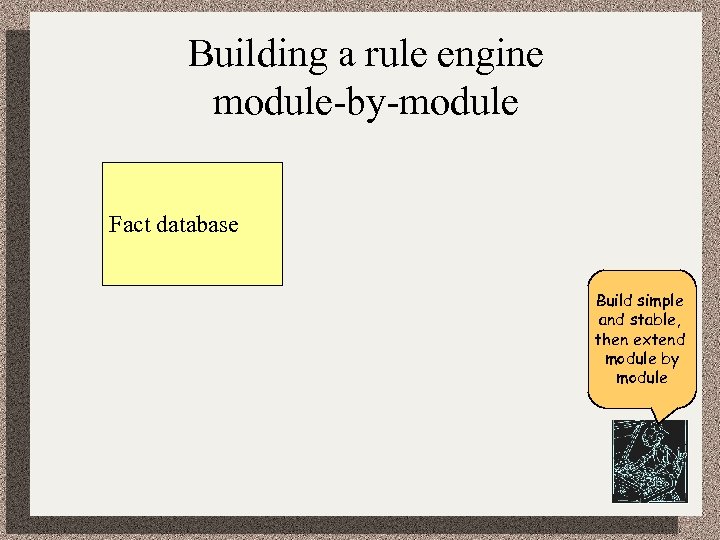Building a rule engine module-by-module Fact database Build simple and stable, then extend module by module

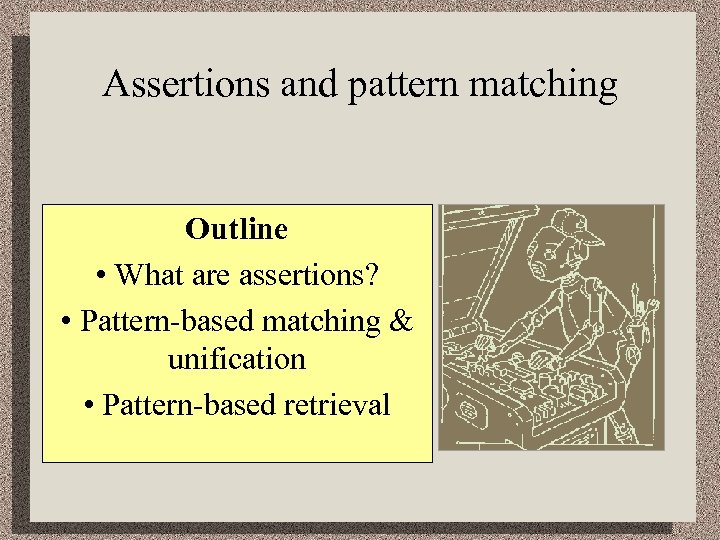Assertions and pattern matching Outline • What are assertions? • Pattern-based matching & unification • Pattern-based retrieval

Assertions • List-based symbolic representations – (this statement is false) – (implies (greeted mary john). (knows mary john)) – (connected-to thigh-bone knee-bone) • In this class, does not presume either predicate calculus or frames • Uses patterns as the basis of category-based reasoning – Select categories via patterns – Instantiate new instances of a category by pattern substitution

Advantages of assertions • Easily composible • Expression of sets via patterns – (on ? x table) : Everything on table. – (block ? x) : Everything that is a block. • Disadvantages – hard to represent levels of belief or relative merit • Alternatives possible

Using pattern matching and unification with assertions • Pattern matching vs. unification – Unification has variables in both pattern and datum – Symmetric operation? Associative? • Many different unifier flavors • Basic algorithm: – tree-walk the pattern and datum – look up and store variables in bindings dictionary as needed

Pattern Matching & Unification (1) (Has-Value (gain ? amp) ? beta) (Has-Value (gain Amplifier 32) 1000) unify assuming the bindings ? amp = Amplifier 32 ? beta = 1000

Pattern Matching & Unification (2) (Mystical ? agent (friend ? x)) (Mystical ? x ? agent ) don’t unify because the bindings ? agent = (friend ? x) ? x = ? agent would result in the infinite expression ? x = (friend …)))

TRE Unify Function • For matching – ? x : Matches symbol, binding to pattern var X – No optional filter field in pattern. – No segment variables. • Matcher returns either a set of bindings (as an alist) or : FAIL. • For substitution of matched patterns – sublis function for instantiating matched patterns.

(F)TRE Unify Function (defun unify (a b &optional (bindings nil)) (cond ((equal a b) bindings) ((variable? a) (unify-variable a b bindings)) ((variable? b) (unify-variable b a bindings)) ((or (not (listp a)) (not (listp b))) : FAIL) ((not (eq : FAIL (setf bindings (unify (first a)(rest b) bindings)))) (unify (rest a) (rest b) bindings)) (t : FAIL)))

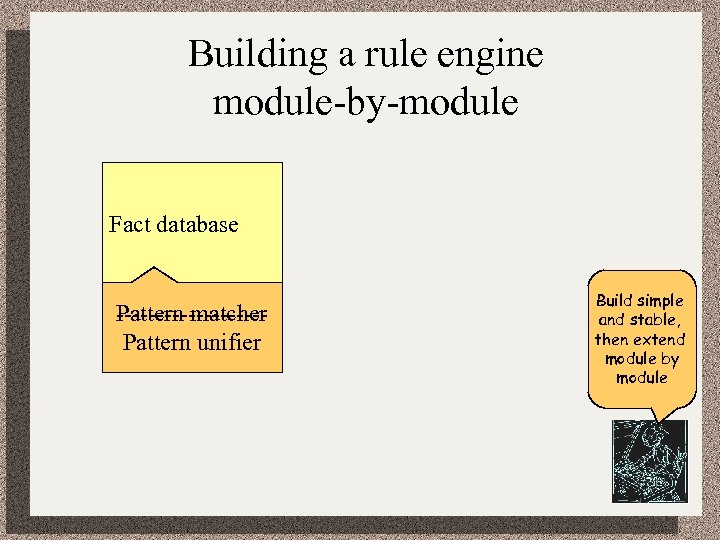Building a rule engine module-by-module Fact database ---------Pattern matcher Pattern unifier Build simple and stable, then extend module by module

Summary and Observations • Unifier algorithm – treewalk pattern and datum – when variable found, do bookkeeping on binding dictionary – fail when conflicting bindings or structural (list to symbol) mismatches • Use of a filter test • Treewalks on fixed patterns can be precompiled (see FTRE)

The rest • Pattern-Directed Inference systems – Pattern-based retrieval – Creating rules • Creating TRE, a Tiny Rule Engine • Creating FTRE – Open-coded unification – Rules with tests and rlet • Application: KM*, a natural deduction method

PDIS Systems Database: Rules: (on block. A table) (on block. B block. A) (red block. B) (white block. A). . . (rule (red ? bl) (small ? b 1)) (rule (on ? b 1 ? b 2) (rule (on ? b 2 table) (assert! (tower ? b 1 ? b 2)))). . .

PDIS Systems Database: Rules: (on block. A table) (on block. B block. A) (red block. B) (white block. A). . . (rule (red ? bl) (small ? b 1)) (rule (on ? b 1 ? b 2) (rule (on ? b 2 table) (assert! (tower ? b 1 ? b 2)))). . .

PDIS Systems Database: Rules: (on block. A table) (on block. B block. A) (red block. B) (white block. A) (small block. B). . (rule (red ? bl) (small ? b 1)) (rule (on ? b 1 ? b 2) (rule (on ? b 2 table) (assert! (tower ? b 1 ? b 2)))). . .

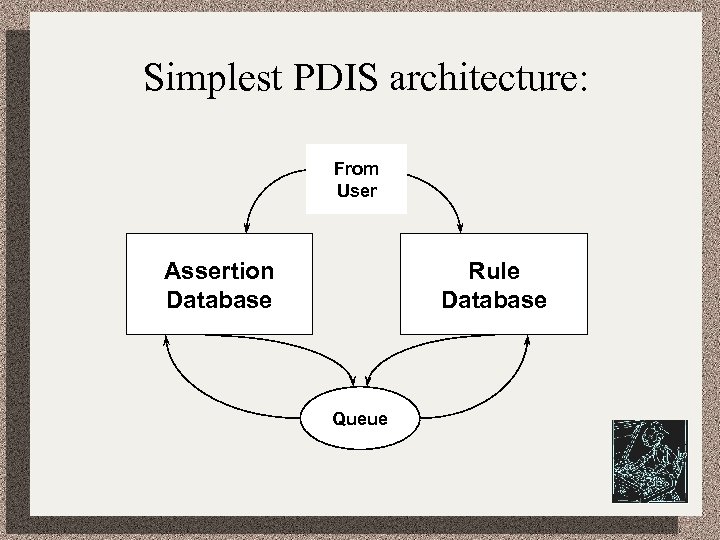Simplest PDIS architecture: From User Assertion Database Rule Database Queue

How do we choose which rules to run against which assertions? • Given a rule trigger, which assertions in the database might match it? • Given an assertion in the database, which rules might be applicable • Basic problem: Pattern-based retrieval

Pattern-based retrieval • Task: Given a pattern, return matching patterns from large set of assertions • Naïve approach: run unify between pattern and each datum – Too expensive! • Two-stage approach: cheap filter for plausible candidates, followed by unify – Much better! But which filter?

Possible filters (1) • Discrimination trees – Pluses: • General over all patterns • Time efficient – Minuses: • Complex bookkeeping • Inefficient use of space

Possible filters (2) • First (or class) indexing – Store rule by first symbol in trigger – Store assertion by first symbol in list – Pluses: • Simple and efficient (time and space) – Minuses: • Can’t handle patterns with variable as first symbol • May store many items under single index • One fix: – CADR (or SECOND) indices for entries that contain many items

Possible filters (3) • Generalized hashing – Multiple hash tables, for indices such as: • First of expression • CADR of expression • Number of items in expression – Retrieve all entries, take intersection – Pluses: • Works on all patterns – Minuses • Really inefficient (time and space) • Seldom used

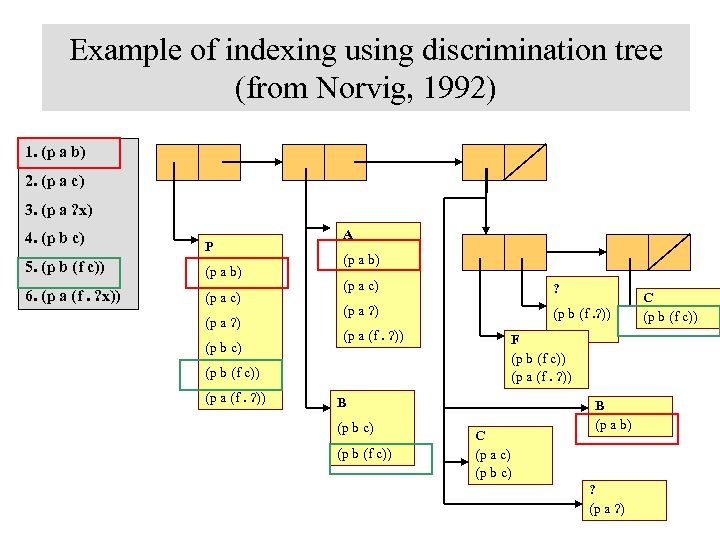Example of indexing using discrimination tree (from Norvig, 1992) 1. (p a b) 2. (p a c) 3. (p a ? x) 4. (p b c) P 5. (p b (f c)) (p a b) 6. (p a (f. ? x)) (p a c) (p a ? ) (p b c) A (p a b) (p a c) ? (p a ? ) (p b (f. ? )) (p a (f. ? )) (p b (f c)) (p a (f. ? )) F (p b (f c)) (p a (f. ? )) B (p b c) (p b (f c)) C (p a c) (p b c) B (p a b) ? (p a ? ) C (p b (f c))

Winner: first indexing • Simplest to implement • For small systems, almost as efficient as discrimination trees

Designing the Tiny Rule Engine (TRE) • Requirements – Pattern matcher, • Matches against a pattern • Can instantiate a particular pattern using a set of bindings – Database of current assertions – Database of current rules – Control mechanism for running rules on assertions

The main interface for TRE • *TRE*, the global variable for the default TRE – dynamically-bound special variable (remember earlier explanation) • (assert! *tre*) – Stores fact in the database • (fetch *tre*) – Retrieves a fact from the database

Implementing the database • Create DBClass struct, which represents a single class index • assert! : – Store in database by dbclass • fetch – Retrieve by dbclass – Unify pattern with retrieved candidates

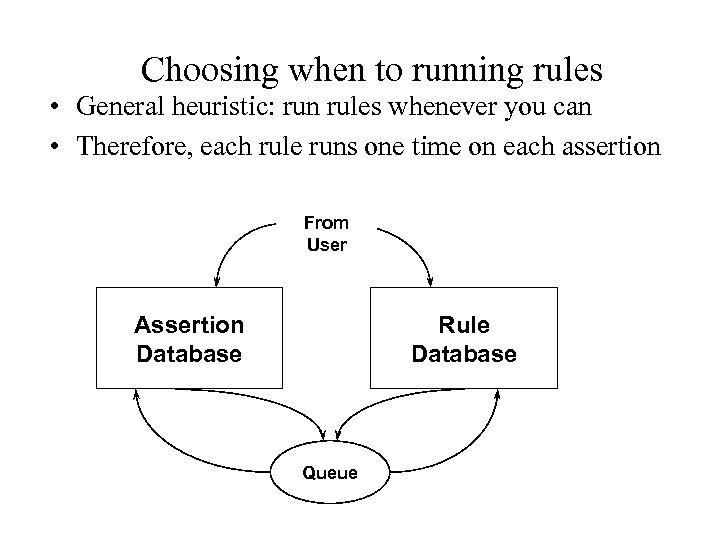Choosing when to running rules • General heuristic: run rules whenever you can • Therefore, each rule runs one time on each assertion From User Assertion Database Rule Database Queue

Pattern-match trigger against database. Making rules for the TRE When match succeeds, evaluate body of rule. • Rule form: (rule (apple ? apple) (assert! `(edible , ? apple))) (rule (apple ? apple) (rule (red ? apple) Rules can create (assert! `(jonathan , ? apple))) other rules.

Properties of rules Indefinite extent: Once spawned, a rule lives forever. Example: (assert! ‘(on a b), (assert! ‘(on b c)) yields same result as (assert! ‘(on a b)), , (assert! ‘(on b c)) Order-independence: An often useful property Results are the same no matter when you add the same set of assertions and rules Example: (assert! ‘(on a b)), (assert! ‘(on b c)) yields same result as (assert! ‘(on b c)), (assert! ‘(on a b))

Design Constraints on TRE • Order-independence => restrictions – All rules are executed eventually. – No deletion – Evil: Using fetch in the body of a rule. • Order-independence => freedom – We can execute rules in any order. – We can interleave adding assertions and triggering rules as convenient

Rule struct in TRE (defstruct (rule (: PRINT-FUNCTION rule-print-procedure)) counter ; Integer to provide unique "name" Dbclass ; Dbclass it is linked to. trigger ; pattern it runs on. body ; code to be evaluated in local environment) ; binding environment.

(rule (apple ? apple) (rule (red ? apple) (assert! `(jonathan , ? apple))) Store rule: trigger: (apple ? apple) body: (rule (red ? apple) (assert! `(jonathan , ? apple))) *env*: NIL (Assert! ‘(apple-23)): triggers rule. Pushed onto queue: bindings: ((? apple-23)) body: (rule (red ? apple) (assert! ‘(jonathan , ? apple))) When run-rules called, pops from queue. *env* == bindings. Store rule: trigger: (red apple-23) body: (assert! `(jonathan apple-23)) *env*: ((? apple. Apple-23))

How good is TRE’s rule mechanism? • Advantages – Simple to implement • Pattern match single trigger • Treat rule body as evaluable function • Rewrite bindings as let statement – Flexible • Disadvantages – Slow (due to eval and unify) – Overly flexible • Rule body could be anything, i. e. , Quicken, Spreadsheet, Ham sandwich…

Summary • Building the TRE module by module – Unifier • Creating a unifier from a pattern matcher – Database • Doing first-indexing via DB-Classes – Alternatives: CADR indexing, discrimination trees – Rule engine • Agenda queue for firing new rules, adding new facts.

Application • Using the FTRE to build a theorem prover – The KM* Natural Deduction System • Assignment – Extending KM*

Example: Natural deduction of logical proofs • A proof is a set of numbered lines • Each line has the form • Example: 27 (implies P Q) 28 P 29 Q asn given (CE 27 28)

Example: Natural deduction of logical proofs • Kalish & Montegue: a set of heuristics for doing logical proofs • Introduction rules – not introduction, and introduction, or introduction, conditional introduction, biconditional introduction • Elimination rules – not elimination, and elimination, or elimination, conditional elimination and biconditional elimination

Kalish & Montegue (cont. ) • Organized along five the different operators: – NOT, AND, OR, IMPLIES (->), and IFF (<=>). • Rules can either eliminate operators or introduce new operators – Elimination rules are simple – Introduction rules are require more control knowledge--cannot be used randomly

Elimination rules • • • AND OR NOT IMPLIES IFF

Not Elimination i (not P)) P (rule (not ? p)) (assert! ? p)) (NE i)

AND Elimination i (and P Q) P Q (AE i)

OR Elimination i j k (or P Q) (implies P R) (implies Q R) R (OE i j k)

Conditional Elimination i j (implies P Q) P Q (CE i j)

Biconditional Elimination i (iff P Q) (implies Q P) (BE i)

Introduction rules - the easy ones • NOT • IFF • AND

Not Introduction i j k show (not P) P. . Q. . (not Q) (NI i j k)

Or Introduction i P (or P Q) (or Q P) (OI i)

And Introduction i j P Q (and P Q) (and Q P) (AI i j) (AI j i)

Introduction rules - the hard ones • OR • IMPLIES

Conditional Introduction i j show (implies P Q) P show Q (CI i j) asn

Biconditional Introduction i j (implies P Q) (implies Q P) (iff P Q) (BI i j)

Simple KM* Example • Premises – If it is spring, there cannot be snow – It snowed this week • Show – It cannot be spring • Formalization – (implies spring (not snow)) – snow – (show (not spring))

1. (implies spring (not snow)) Premise 2. snow Premise 3. (show (not spring))

1. (implies spring (not snow)) Premise 2. snow Premise 3. (show (not spring)) 4. spring Asn

1. (implies spring (not snow)) Premise 2. snow Premise 3. (show (not spring)) 4. spring Asn 5. (not snow) (CE 1 4)

1. 2. 3. 4. 5. (implies spring (not snow)) Premise snow Premise (show (not spring)) (NI 4 2 5) spring Asn (not snow) (CE 1 4)

Implementing KM* in TRE • How to do boxes? • Elimination rules are easy • Introduction rules are harder

Classic problem: Positive Feedback Loops • • • Examples: And introduction, Or elimination Strategy: Limit applicability of rules syntactically Strategy: Reason about when to apply rules Insight: Many control decisions are non-local. Implication: Often need more global mechanism that feeds off locally determined alternatives to organize problem solving

Rest of lecture • Moving beyond monotonicity – How to make assumptions – How to retract assumptions cleanly – How to set up a dependency network so that you don’t make that mistake again • Context mechanism for FTRE

FTRE: An improved version of TRE • Speeds up pattern-based retrieval using opencoded unification • Provides more powerful, easier-to-read rules • Adds context mechanism

FTRE rule syntax • Aimed at convenience – Triggers are now a list, interpreted conjunctively – rassert! to remove backquotes • Examples (rule (show ? q) (rule (implies ? p ? q) (assert! `(show , ? p)))) becomes (rule ((show ? q) (implies ? p ? q)) (rassert! (show ? p)))

FTRE Syntax: Trigger keywords • : VAR = next item is a variable to be bound to entire preceding trigger pattern • : TEST = next item is lisp code executed in environment so far. If NIL, match fails. • Example: (rule ((show ? q) : test (not (fetch ? q)) (implies ? p ? q) : var ? imp) (debug-nd “~% BC-CE: Looking for ~A to use ~A. . ” ? p ? imp) (rassert! (show ? p)))

Making RASSERT! work (defmacro rassert! (fact) `(assert! , (quotize fact))) (defun quotize (pattern) "Given pattern, create evaluatable form that will return the original pattern, but also replace pattern variables with their bindings. " (cond ((null pattern) nil) ((variable? pattern) ((not (listp pattern)) (list 'QUOTE pattern)) ((eq (first pattern) : EVAL) (cadr pattern)) (t `(cons , (quotize (first pattern)) , (quotize (rest pattern))))))

Making RASSERT! work > (quotize '(foo ? bar ? bat)) (CONS 'FOO (CONS ? BAR (CONS ? BAT NIL))) > (macroexpand-1 '(rassert! (foo ? bar ? bat))) (ASSERT! (CONS 'FOO (CONS ? BAR (CONS ? BAT NIL)))) … which is equivalent to… (assert! `(foo , ? bar , ? bat))

Efficiency trick: Precompiling matcher and body • FTRE Rule struct (defstruct (rule (: PRINT-FUNCTION ftre-rule-printer)) id ; unique "name" Dbclass ; Dbclass it is linked to. matcher ; procedure that performs the match. body ; procedure that does the rule's work. assumption? ) ; Does it make an assumption?

Open-coded unification • We can create a compilable matcher for any given pattern • We’ll use these specialized match functions to make rules faster

Implementation issues for efficient rules & open-coded unification • At rule expansion time, must process all subrules. • Must keep track of variables that will be bound at run-time, to ensure that the appropriate lexical scoping is enforced. • Tests performed by the unifier must be “unrolled” into a procedure. • The rule and body procedures must have their argument lists set up correctly. • Here’s what it looks like: brace yourself!

Problem with FTRE’s • Gullible – They believe anything you tell them • Strong-minded – Once they believe something, you can’t tell them not to believe it • How do we get around this? • Needed for Natural Deduction

Context mechanism for FTRE • Add assumption to FTRE – All subsequent rules and assertions inferred from assumption are part of its “context” – If that assumption is retracted, rules and assertions in that context are also removed • Contexts can be created within other contexts – Similar to scoping of closures (environments)

How contexts work P (show P) (not Q) (implies (not P) Q) (implies (not Q) R) (not P) Q Contradiction!

Some requirements • One context per assumption • Assertions stored in most recent context • Rules which create assumptions must run after all rules that do not • All rules must be run to quiescence in one context before another context is created

Mechanics of the context mechanism • Add context stack to FTRE’s database – Add slots to FTRE struct to include local rules and assertions – Modify assert! and fetch to use the local context • Let rules use context – Pre-mark rules which create assumptions – Search via depth-first search (why? ) • Specific mechanism – Seek for goal in context

Adding a context stack mechanism to the FTRE (defstruct (ftre (: PRINT-FUNCTION ftre-printer)) title (dbclass-table nil) ; ; Hash table of class-indexed dbclasses. (debugging nil) ; ; When non-NIL, print debugging information. (debugging-contexts nil) ; ; When non-NIL, print debugging on contexts. (normal-queue nil) ; ; Holds rules that do not make assumptions. (asn-queue nil) ; ; Holds rules that make assumptions. (depth 0) ; ; Current stack depth for context mechanism. (max-depth 5) ; ; Maximum depth allowed. (local-data nil) ; ; Data local to the context. (local-rules nil) ; ; Rules local to the context. (rule-counter 0) ; ; Number of rules. (rules-run 0)) ; ; Number of rules run.

Changing assert! to handle contexts (defun insert (fact ftre &aux dbclass) "Insert a single fact into the FTRE's database. " (when (null fact) (error "~% Can't assert NIL. ")) (setf dbclass (get-dbclass fact ftre)) (cond ((member fact (dbclass-facts dbclass) : TEST #'equal) nil) ((= (ftre-depth ftre) 0) (push fact (dbclass-facts dbclass))) Store global ((member fact (ftre-local-data ftre) data when depth : TEST #'equal) nil) is zero (t (push fact (ftre-local-data *ftre*))))) Store local data otherwise

Changing fetch to handle contexts (defun fetch (pattern &optional (*ftre*) &aux bindings unifiers) "Given a pattern, retrieve all matching facts from the database. " (dolist (candidate (get-candidates pattern *ftre*) unifiers) (setf bindings (unify pattern candidate)) (unless (eq bindings : FAIL) (push (sublis bindings pattern) unifiers)))) (defun get-candidates (pattern ftre) "Get potentially matching facts from FTRE database. " (append (ftre-local-data ftre) (dbclass-facts (get-dbclass pattern ftre))))

Pre-marking rules that generate assumptions (defstruct (rule (: PRINT-FUNCTION ftre-rule-printer)) id ; unique "name" Dbclass ; Dbclass it is linked to. matcher ; procedure that performs the match. body ; procedure that does the rule's work. assumption? ) ; Does it make an assumption? (defmacro rule (triggers &rest body) "Create a rule with the given triggersand body. " (do-rule (parse-triggers) body nil)) (defmacro a-rule (triggers &rest body) "Create an assumption-making rule. " (do-rule (parse-triggers) body T)) ; ; Restriction: An a-rule can have only one trigger!

Controlling how rules are run • Two rule queues: one for a-rules, one for regular – Always pop off the assumption-making rules last (defun enqueue (ftre new asn? ) "Queue a new fact in either the regular or assumption queue. " (if asn? (push new (ftre-asn-queue ftre)) (push new (ftre-normal-queue ftre)))) (defun dequeue (ftre) "Pop a fact from the queue. " (if (ftre-normal-queue ftre) (pop (ftre-normal-queue ftre)) (pop (ftre-asn-queue ftre))))

Try-in-context • Algorithm – Save the current local data and clear execution queue – Assert assumption and run rules to quiescence – Execute any form (e. g. , a fetch) on the produced database – Restore the old context, throwing out any data or rules produced in the new context

Saving and restoring state (defun save-context (ftre) (prog 1 (list (ftre-local-data ftre) (ftre-local-rules ftre) (ftre-normal-queue ftre) (ftre-asn-queue ftre)) (setf (ftre-normal-queue ftre) NIL (ftre-asn-queue ftre) NIL) (incf (ftre-depth ftre)) (push (ftre-depth ftre) (ftre-local-data ftre)))) (defun restore-context (ftre saved-context) "Restore the saved context in the FTRE. " (setf (ftre-local-data *ftre*) (first saved-context) (ftre-local-rules *ftre*) (second saved-context) (ftre-normal-queue *ftre*) (third saved-context) (ftre-asn-queue *ftre*) (fourth saved-context)) (decf (ftre-depth *ftre*)) ftre)

" src="https://present5.com/presentation/602716a7f053d70852944980dc33d5c7/image-86.jpg" alt="Try-in-context (defun try-in-context (assumption form &optional (*ftre*) &aux (depth 0)) "Create context where " /> Try-in-context (defun try-in-context (assumption form &optional (*ftre*) &aux (depth 0)) "Create context where is valid, run rules, and return value for

" src="https://present5.com/presentation/602716a7f053d70852944980dc33d5c7/image-87.jpg" alt="Try-in-context (defun try-in-context (assumption form &optional (*ftre*) &aux (depth 0)) "Create context where " /> Try-in-context (defun try-in-context (assumption form &optional (*ftre*) &aux (depth 0)) "Create context where is valid, run rules, and return value for before popping context. " (setf depth (ftre-depth *ftre*)) (when (> depth (ftre-max-depth *ftre*)) (debugging-contexts "~% ~A(~D): Punting on trying ~A, too deep. " Test context *ftre* (ftre-depth *ftre*) assumption) (return-from TRY-IN-CONTEXT nil)) (let ((old-context (save-context *ftre*))) (with-ftre *ftre* (if assumption (assert! assumption)) (run-rules *ftre*) (setf result (eval form)) (restore-context *ftre* old-context) result))) depth

" src="https://present5.com/presentation/602716a7f053d70852944980dc33d5c7/image-88.jpg" alt="Try-in-context (defun try-in-context (assumption form &optional (*ftre*) &aux (depth 0)) "Create context where " /> Try-in-context (defun try-in-context (assumption form &optional (*ftre*) &aux (depth 0)) "Create context where is valid, run rules, and return value for before popping context. " (setf depth (ftre-depth *ftre*)) (when (> depth (ftre-max-depth *ftre*)) (debugging-contexts "~% ~A(~D): Punting on trying ~A, too deep. " *ftre* (ftre-depth *ftre*) assumption) (return-from TRY-IN-CONTEXT nil)) (let ((old-context (save-context *ftre*))) (with-ftre *ftre* (if assumption (assert! assumption)) (run-rules *ftre*) (setf result (eval form)) (restore-context *ftre* old-context) result))) Make assumption, run rules, and test result of evaluating form.

Seek-in-context (defun seek-in-context (assumption form &optional (*ftre*) &aux (dept 0)) (let ((depth (ftre-depth *ftre*))) (when (> depth (ftre-max-depth *ftre*)) (debugging-contexts "~% ~A(~D): Punting on assuming ~A; " *ftre* depth assumption ) (return-from SEEK-IN-CONTEXT nil)) Same as Try-incontext, but create (let ((old-context (save-context *ftre*))) (if assumption (assert! assumption *ftre*)) rule that returns when goal is found. (with-ftre *ftre* (assert! `(show , goal)) (eval `(rule (, goal) (when (= (ftre-depth *ftre*) , (ftre-depth *ftre*)) ; ; Found goal. (throw 'punt-context t))))) (catch 'punt-context (run-rules *ftre*)) (debugging-contexts "~% ~A(~D): Retracting ~A, sought ~A. " *ftre* (ftre-depth *ftre*) assumption goal) (setf result (fetch goal)) (restore-context ftre old-context)

Calling seek-in-context from assumption rules (a-rule ((show ? p) ; indirect proof. : TEST (not (or (fetch ? p) (eq ? p 'contradiction) (not (simple-proposition? ? p))))) (debug-nd "~%~D: IP attempt: ~A. " (ftre-depth *ftre*) ? p) (when (seek-in-context `(not , ? p) 'contradiction) (debug-nd "~%~D: IP: ~A" (ftre-depth *ftre*) ? p) (rassert! ? p)))

Examples from ND These examples are part of the FTRE distribution *debug-nd* flag before running). Example 1: (implies p q) (not q) (show (not p)) Example 2: (or (not P) R)) (implies R Q) (show (implies P Q)) (Be sure to turn on

Summary: Creating contexts • Modifications to FTRE – local rule and data slots, additional queue for assumption-creating rules – mark assumption-creating rules explicitly – to run context, use TRY-IN-CONTEXT or SEEK-IN-CONTEXT as body of rule • TRY-IN-CONTEXT – save state, run rules, check result, restore state

Truth-Maintenance Systems Are Coming Next