a6bdbec2221e4450272c42c92cac9db6.ppt
- Количество слайдов: 77


PATH PLANNING Presented by : Mohamadreza Negahdar Supervisor : Dr. Ahmadian Co-Supervisor : Prof. Navab Tehran University of Medical Sciences October 5 , 2005

OUTLINE n n n n Introduction Path planning in medicine Automatic path generation Skeleton & skeletonization Skeletonization techniques Medical applications Path planning n n n n Roadmap Cell decomposition Potential field Virtual endoscopy Navigation Applications Our work

Introduction n n How can “see” inside the body to screen and cure? Centerline extraction is the basis to understand three dimensional structure of the organ Given a map and goal location, identify trajectory to reach goal location Strategic competence How do we combine these two competencies, along with localization, and mapping, into a coherent framework?

Path Planning in medicine n Fly-through and navigation n General idea of the shape of the organ walls n Detect an abnormal shape n Making measurements for locating abnormalities n Computing local distension and length n Risk of infection or perforation of the anatomy being examined will be eliminated
Path Planning in medicine n n n n Bronchoscopy, Airway analysis Colonoscopy Esophagus Neurosurgery, Stereotaxic radiosurgery Liver surgery Angiography Needle steering
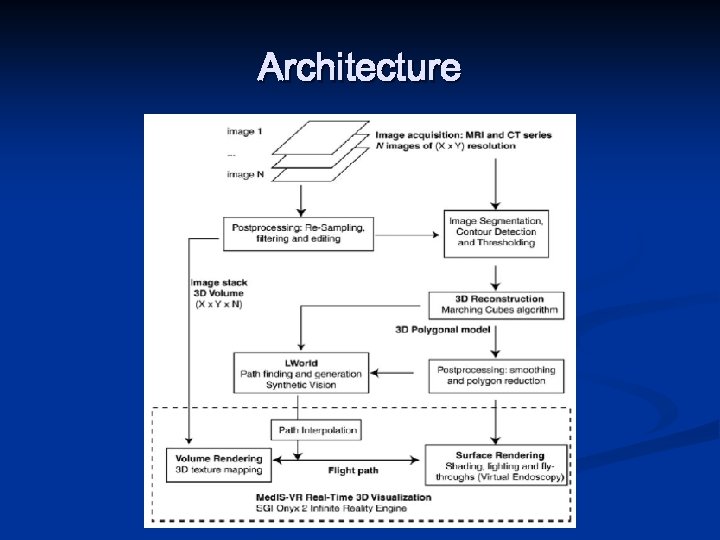
Architecture

Restrictions of manually path planning n Very time consuming n Frustrating for a novice user n Need to improve the performance and lower the cost ü For this reason, we provide the surgeon with an automatic path generation.

Automatic Path Generation n Surgeon loads a 3 D model n Defines a start and an end point n n Program returns an optimal path centered inside the model The user can fly-through the path and/or edit it manually
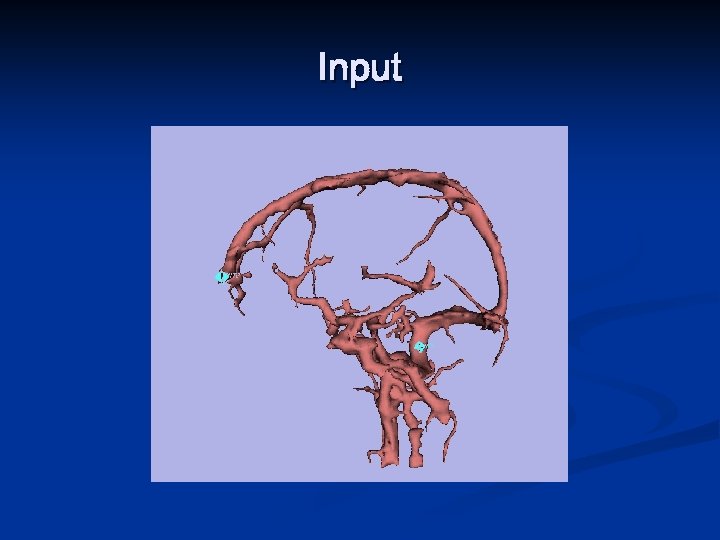
Input
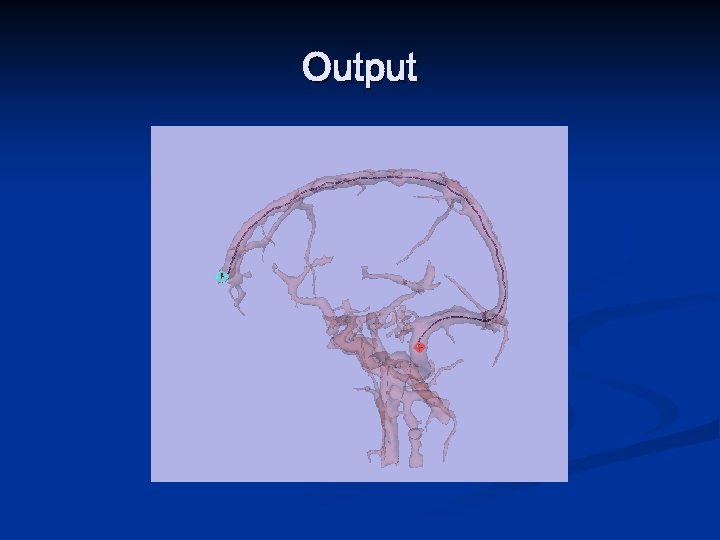
Output
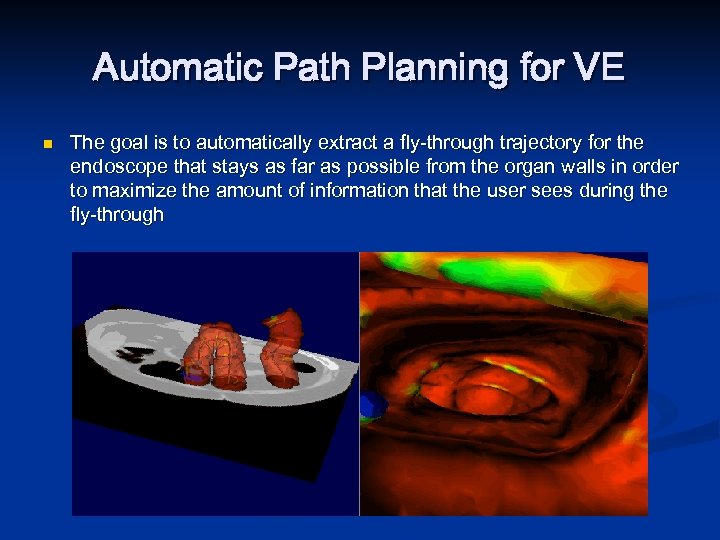
Automatic Path Planning for VE n The goal is to automatically extract a fly-through trajectory for the endoscope that stays as far as possible from the organ walls in order to maximize the amount of information that the user sees during the fly-through

Skeletonization n n The aim of the skeletonization is to extract a region-based shape feature representing the general form of an object. We have applied skeletonization to extract the central path of a 3 D "tubular" object.

Skeleton of object n n The medial axis from an object called its skeleton Skeleton-based techniques first compute a digital skeleton of the entire tree Center locus of multi-tangent circles (in 2 D) or balls (in 3 D) The skeleton represents: local object symmetries, and the topological structure of the object.

Skeletonization techniques n n n detecting ridges in distance map of the boundary points calculating the Voronoi diagram generated by the boundary points the layer by layer erosion called thinning

Comparison of Skeletonization Techniques n In digital spaces, only an approximation to the "true skeleton" can be extracted. There are two requirements to be complied with: n n topological (to retain the topology of the original object) geometrical (forcing the "skeleton" being in the middle of the object and invariance under the most important geometrical transformation including translation, rotation, and scaling) method geometrical topological Distance transform yes no Voronoi-skeleton yes Thinning no yes

Distance Transformation n Ø The original (binary) image is converted into feature and non-feature elements. The feature elements belong to the boundary of the object. The distance map is generated where each element gives the distance to the nearest feature element. The ridges (local extremes) are detected as skeletal points. The distance map resulted by the distance transformation depends on the chosen distance. The original binary object (left) and its distance map (right). (The distance map is displayed as a surface where the ridge points belong to the skeleton. )
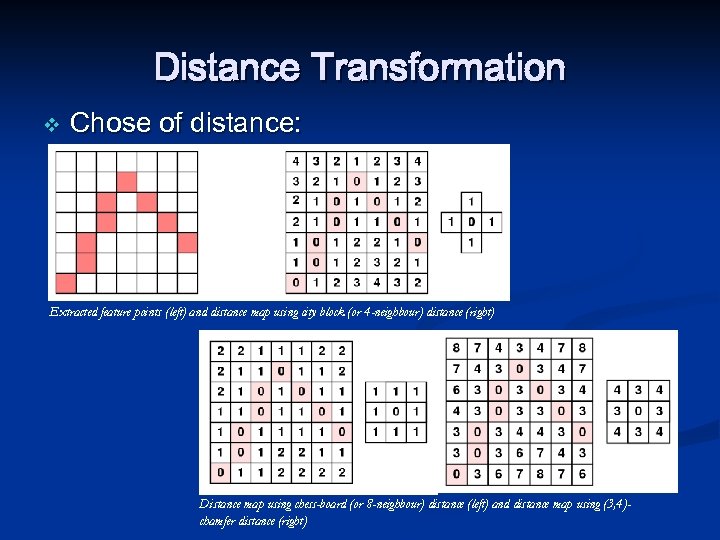
Distance Transformation v Chose of distance: Extracted feature points (left) and distance map using city block (or 4 -neighbour) distance (right) Distance map using chess-board (or 8 -neighbour) distance (left) and distance map using (3, 4)chamfer distance (right)

Voronoi Diagram n The Voronoi diagram of a discrete set of points (called generating points) is the partition of the given space into cells so that each cell contains exactly one generating point and the locus of all points which are nearer to this generating point than to other generating points. The 10 generating points (left) and their Voronoi diagram (right).
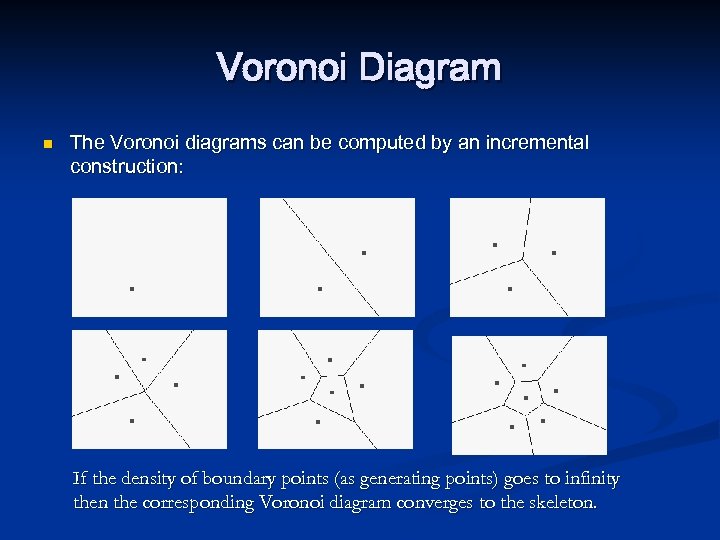
Voronoi Diagram n The Voronoi diagrams can be computed by an incremental construction: If the density of boundary points (as generating points) goes to infinity then the corresponding Voronoi diagram converges to the skeleton.
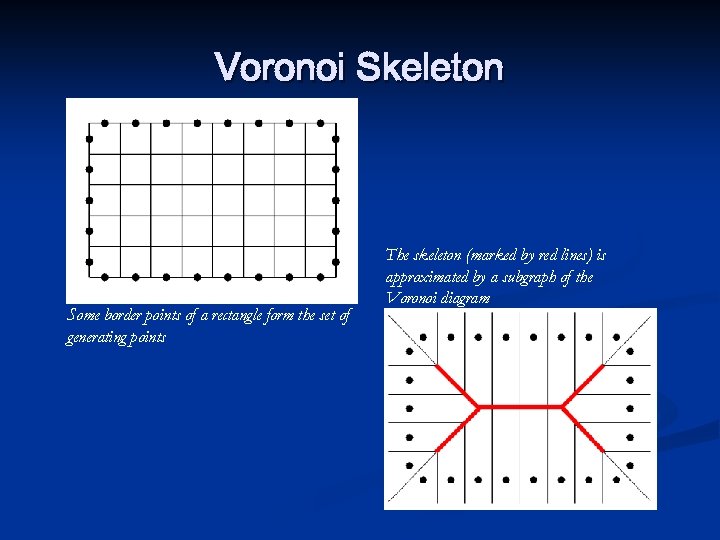
Voronoi Skeleton Some border points of a rectangle form the set of generating points The skeleton (marked by red lines) is approximated by a subgraph of the Voronoi diagram

Thinning n n Border points of a binary object are deleted in iteration steps until only the “skeleton” is left. In case of “near tubular” 3 D objects (e. g. , airway, blood vessel, and gastro–intestinal tract), Thinning has a major advantage over the other skeletonization methods since curve thinning can produces medial lines easily
Thinning

Thinning n The thinning has some beneficial properties: n n n It preserves the topology (retains the topology of the original object) It preserves the shape (significant feature suitable for object recognition or classification is extracted) It forces the "skeleton" being in the middle of the object It produces one pixel/voxel width "skeleton“ It does not preserve the topology, since n n n an object is disconnected an object is completely deleted cavity (white connected component surrounded by an object) is created/a hole is created a cavity/hole is merged with the background two cavities/four holes are merged
Thinning

Medical Applications n assessment of laryngotracheal stenosis n assessment of infrarenal aortic aneurysm n unravelling the colon Ø Each of the emerged three applications requires the cross-sectional profiles of the investigated tubular organs

Procedure n n image acquisition by Spiral Computed Tomography (S-CT) (semiautomatic snake-based) segmentation (i. e. , determining a binary object from the gray-level picture n morphological filtering of the segmented object n curve thinning (by using one of our 3 D thinning algorithm) n raster-to-vector conversion n pruning the vector structure (i. e. , removing the unwanted branches) n smoothing the resulted central path n calculation of the cross-sectional profile orthogonal to the central path
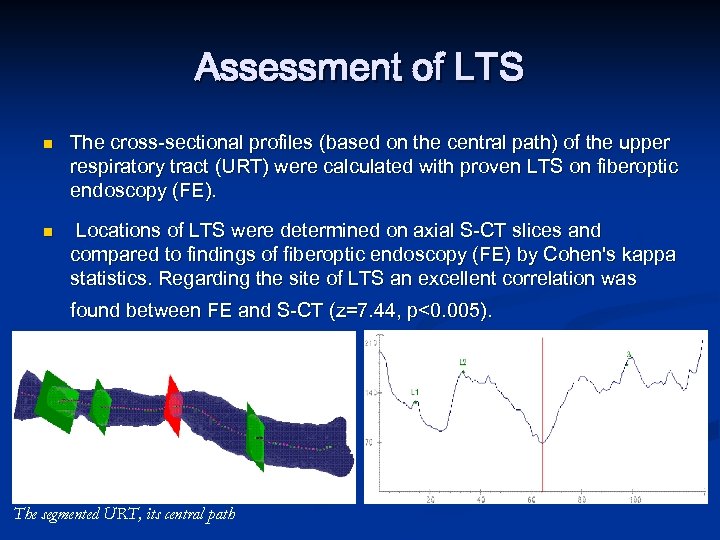
Assessment of LTS n n The cross-sectional profiles (based on the central path) of the upper respiratory tract (URT) were calculated with proven LTS on fiberoptic endoscopy (FE). Locations of LTS were determined on axial S-CT slices and compared to findings of fiberoptic endoscopy (FE) by Cohen's kappa statistics. Regarding the site of LTS an excellent correlation was found between FE and S-CT (z=7. 44, p<0. 005). The segmented URT, its central path
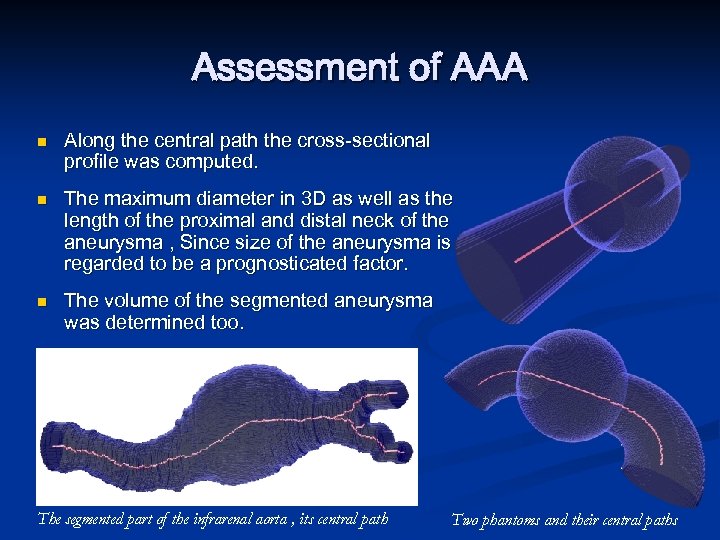
Assessment of AAA n n n Along the central path the cross-sectional profile was computed. The maximum diameter in 3 D as well as the length of the proximal and distal neck of the aneurysma , Since size of the aneurysma is regarded to be a prognosticated factor. The volume of the segmented aneurysma was determined too. The segmented part of the infrarenal aorta , its central path Two phantoms and their central paths

Unravelling the Colon n n Unravelling the colon is a new method to visualize the entire inner surface of the colon without the need for navigation. This is a minimally invasive technique that can be used for colorectal polyps and cancer detection. An algorithm for unravelling the colon which is to digitally straighten and then flatten using reconstructed spiral/helical computer tomograph (CT) images. Comparing to virtual colonoscopy where polyps may be hidden from view behind the folds, the unravelled colon is more suitable for polyp detection, because the entire inner surface is displayed at one view.
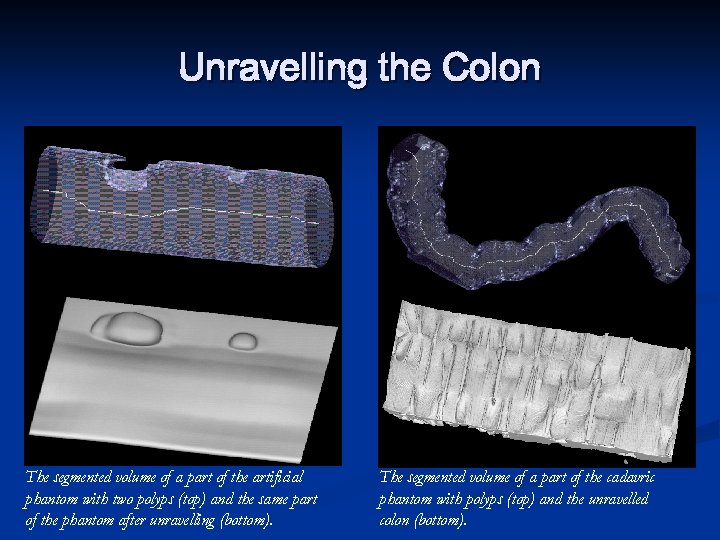
Unravelling the Colon The segmented volume of a part of the artificial phantom with two polyps (top) and the same part of the phantom after unravelling (bottom). The segmented volume of a part of the cadavric phantom with polyps (top) and the unravelled colon (bottom).
PATH PLANNING Approaches; Roadmap road map using Meadow maps road map using visibility graph road map using Voronoi diagram v RRT Cell decomposition exact cell decomposition approximate cell decomposition adaptive cell decomposition Potential field

Roadmap n n n Building a network connection between the vertices of polygons Typically represent obstacles as polygons, and the camera as a point Appropriate for polygon-based dataset , has limitation in VC
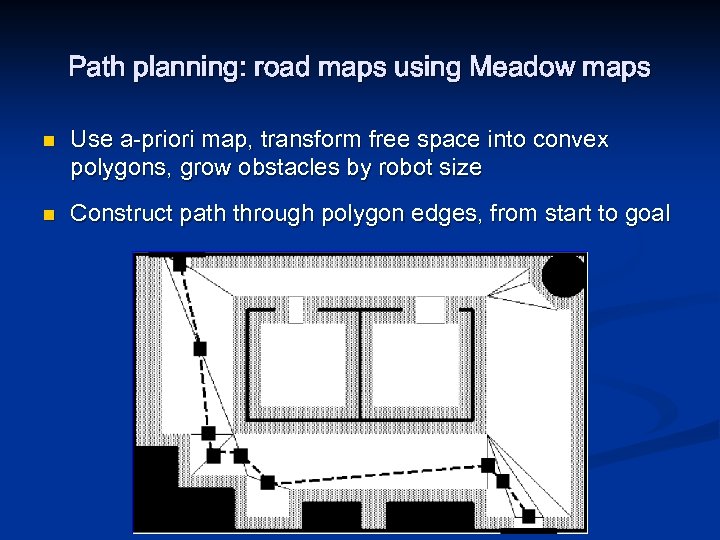
Path planning: road maps using Meadow maps n n Use a-priori map, transform free space into convex polygons, grow obstacles by robot size Construct path through polygon edges, from start to goal
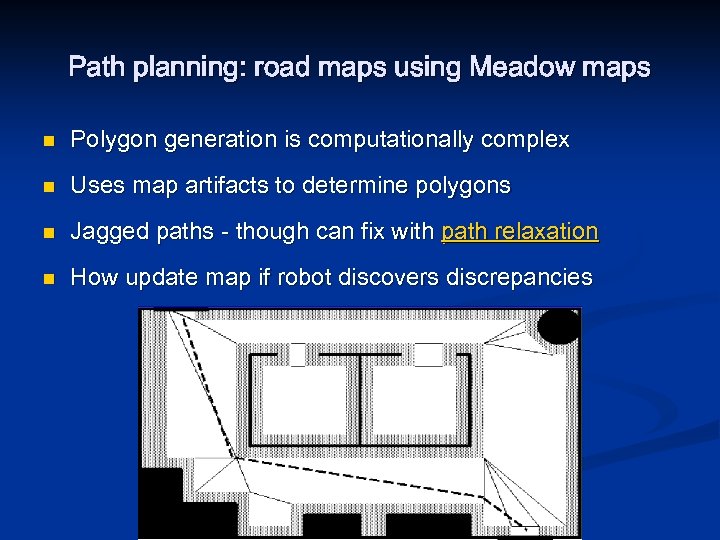
Path planning: road maps using Meadow maps n Polygon generation is computationally complex n Uses map artifacts to determine polygons n Jagged paths - though can fix with path relaxation n How update map if robot discovers discrepancies
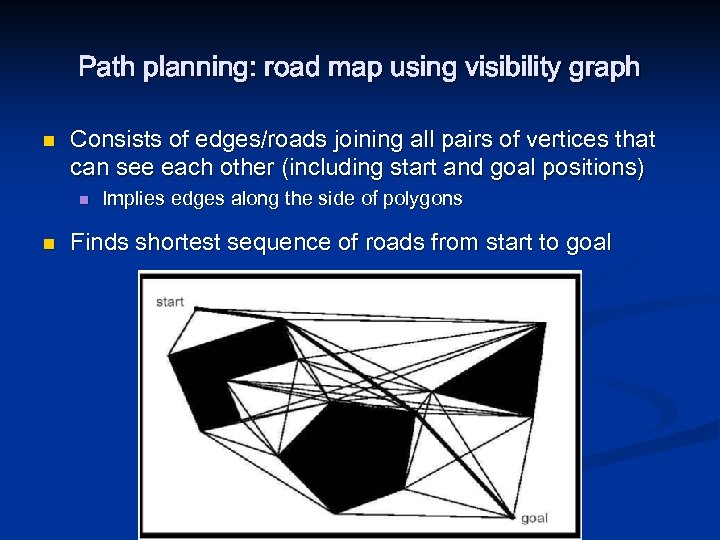
Path planning: road map using visibility graph n Consists of edges/roads joining all pairs of vertices that can see each other (including start and goal positions) n n Implies edges along the side of polygons Finds shortest sequence of roads from start to goal
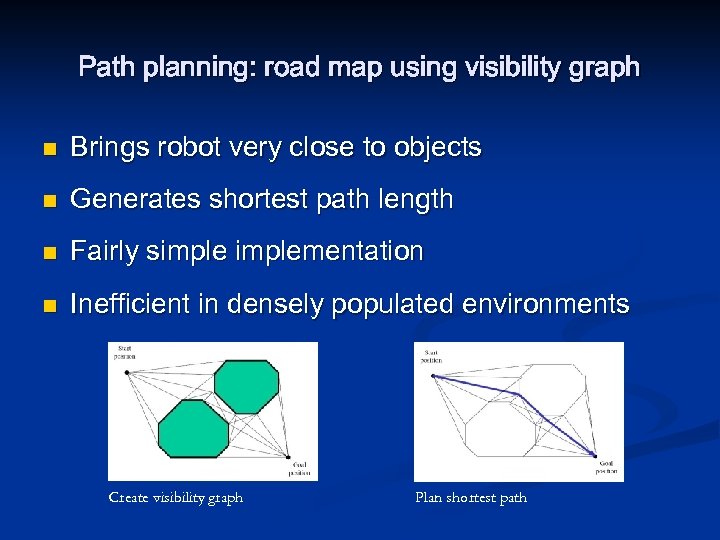
Path planning: road map using visibility graph n Brings robot very close to objects n Generates shortest path length n Fairly simplementation n Inefficient in densely populated environments Create visibility graph Plan shortest path
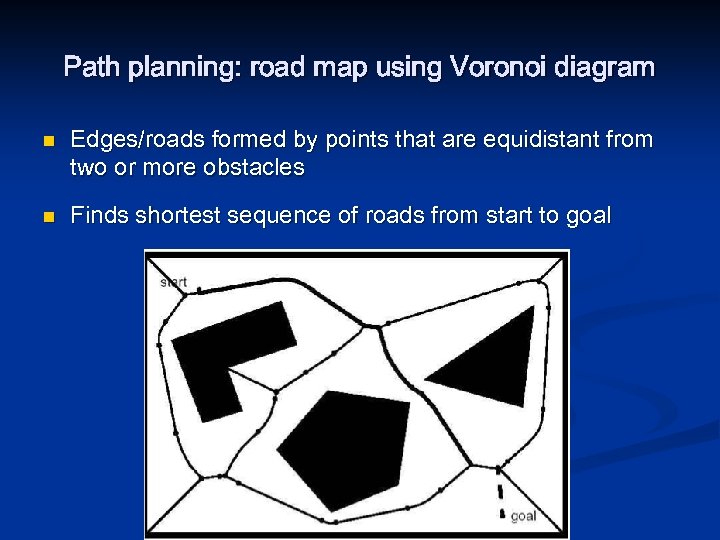
Path planning: road map using Voronoi diagram n n Edges/roads formed by points that are equidistant from two or more obstacles Finds shortest sequence of roads from start to goal
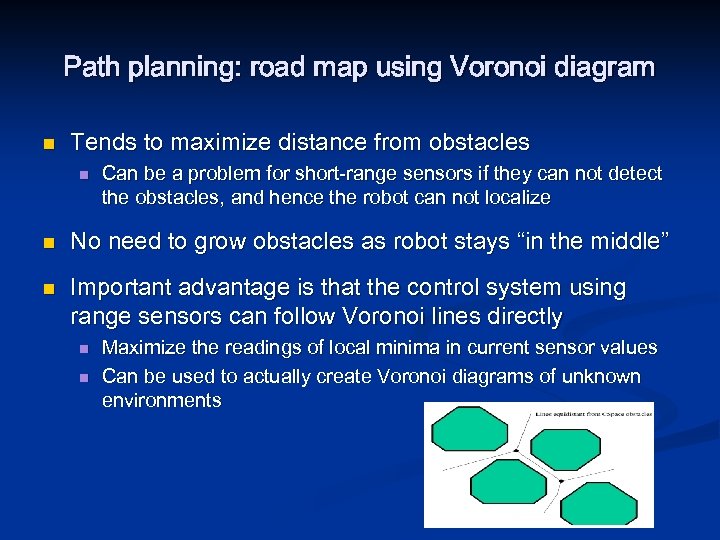
Path planning: road map using Voronoi diagram n Tends to maximize distance from obstacles n n n Can be a problem for short-range sensors if they can not detect the obstacles, and hence the robot can not localize No need to grow obstacles as robot stays “in the middle” Important advantage is that the control system using range sensors can follow Voronoi lines directly n n Maximize the readings of local minima in current sensor values Can be used to actually create Voronoi diagrams of unknown environments
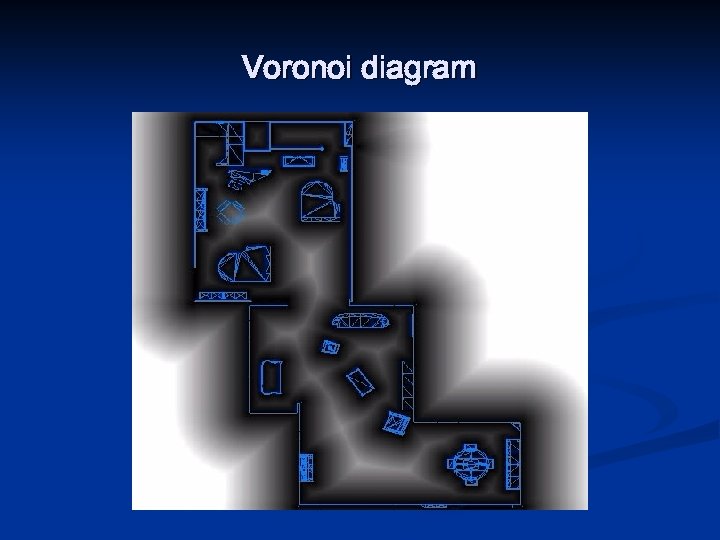
Voronoi diagram

Rapidly-exploring Random trees v v Begin at the start state Attempt to grow into the goal state By exploring the vehicle’s state space Search from both sides Goal Start
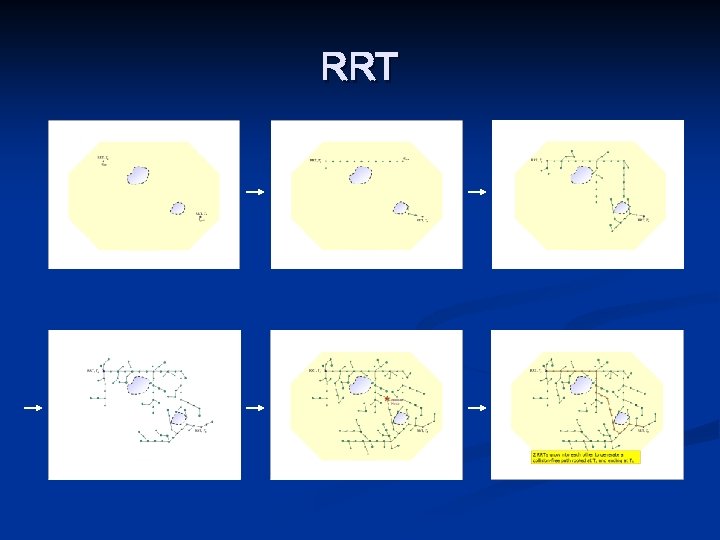
RRT
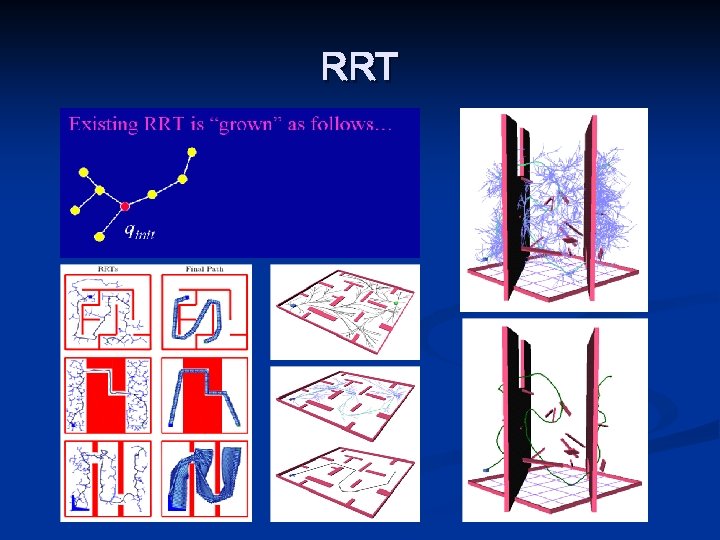
RRT

Cell decomposition n Divide space into simple connected regions called cells n Construct connectivity graph from adjacent open cells n n Find cells containing start and goal locations, and search for path between them in the connectivity graph Compute path within each cell found in path above, e. g. n n Pass through midpoints of cell boundaries Sequence of wall-following motions and straight line movements
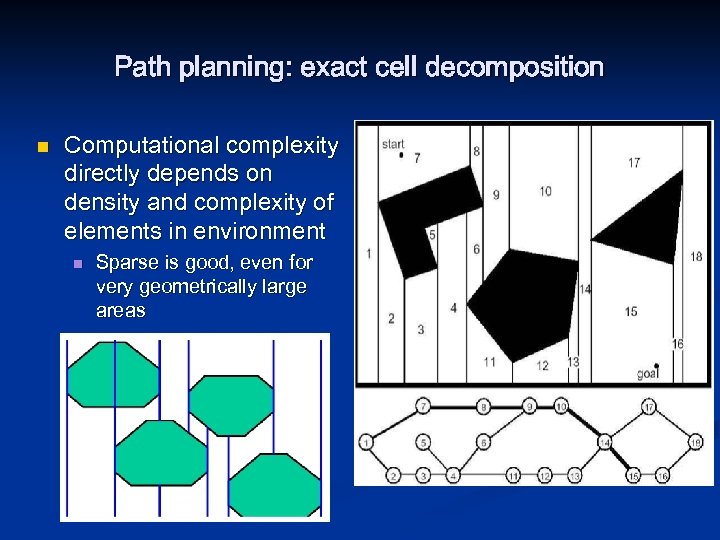
Path planning: exact cell decomposition n Computational complexity directly depends on density and complexity of elements in environment n Sparse is good, even for very geometrically large areas
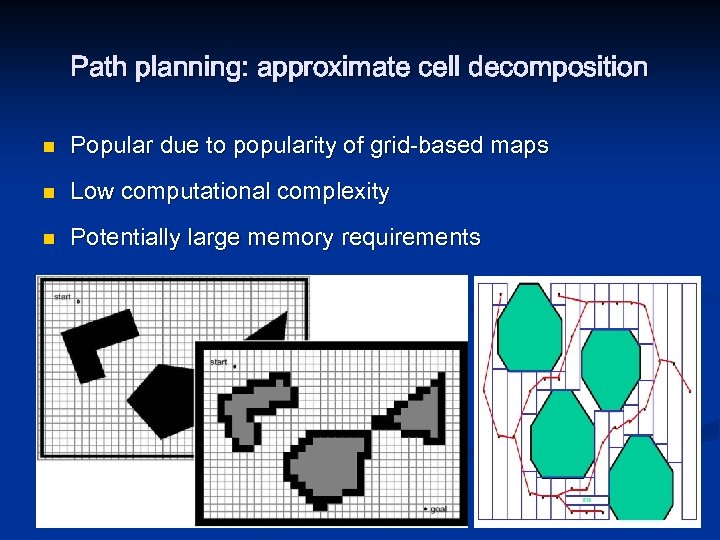
Path planning: approximate cell decomposition n Popular due to popularity of grid-based maps n Low computational complexity n Potentially large memory requirements

Path planning: approximate cell decomposition n NF 1, ‘grassfire’, algorithm n n n Minima-free Wavefront expansion from goal outwards Each cell visited once - computational complexity linear in number of cells, not environment complexity
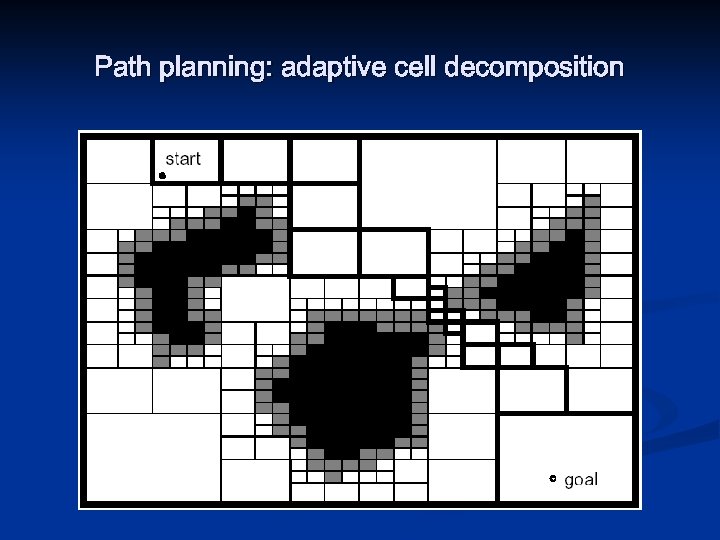
Path planning: adaptive cell decomposition

Potential field n n This approaches is simplified to a point such as a camera model in computer graphics The camera moves under the influence of a set of potentials produced by the attraction and repulsion potentials The attraction potential pulls robot toward the goal and the repulsion potential pushes it away from the obstacles The variation of potentials create the attraction and repulsion forces
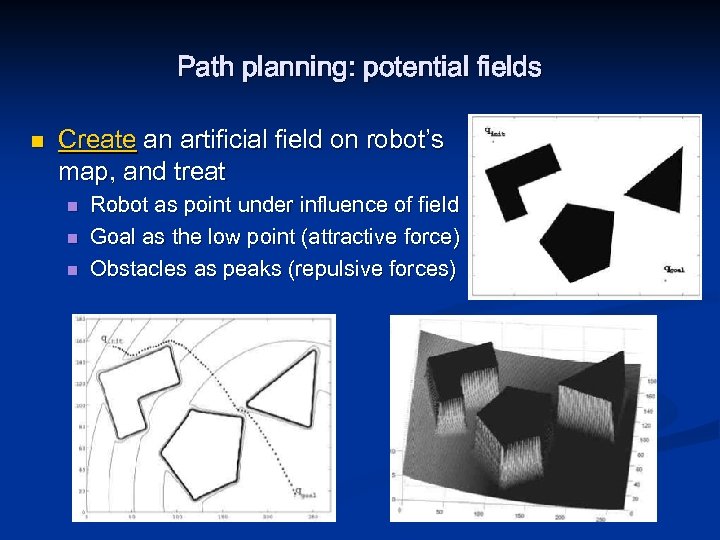
Path planning: potential fields n Create an artificial field on robot’s map, and treat n n n Robot as point under influence of field Goal as the low point (attractive force) Obstacles as peaks (repulsive forces)

Path planning: potential fields n Fairly easy to implement n Set robot speed proportional to force n n n Field drives robot to the goal Movement is similar to a ball rolling down a hill Is also a control law as robot can always determine next required action (assuming robot can localize position with respect to its map and the field) n Local minima can be problematic n Concave objects can generate oscillations n More complicated if robot is not treated as point mass
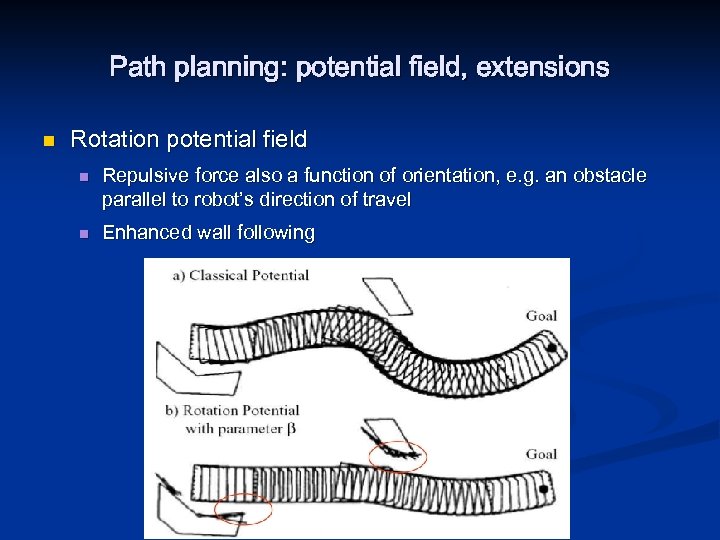
Path planning: potential field, extensions n Rotation potential field n n Repulsive force also a function of orientation, e. g. an obstacle parallel to robot’s direction of travel Enhanced wall following
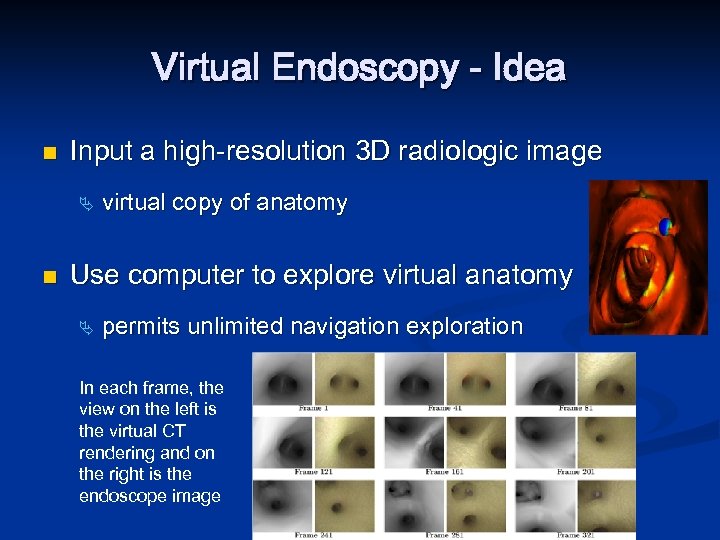
Virtual Endoscopy - Idea n Input a high-resolution 3 D radiologic image Ä n virtual copy of anatomy Use computer to explore virtual anatomy Ä permits unlimited navigation exploration In each frame, the view on the left is the virtual CT rendering and on the right is the endoscope image

Navigation n n The camera automatically moves from the source point towards the target point User can interactively modified the camera position and direction The camera stays away from the surface The camera should never penetrate through the surface The physician change source and target positions
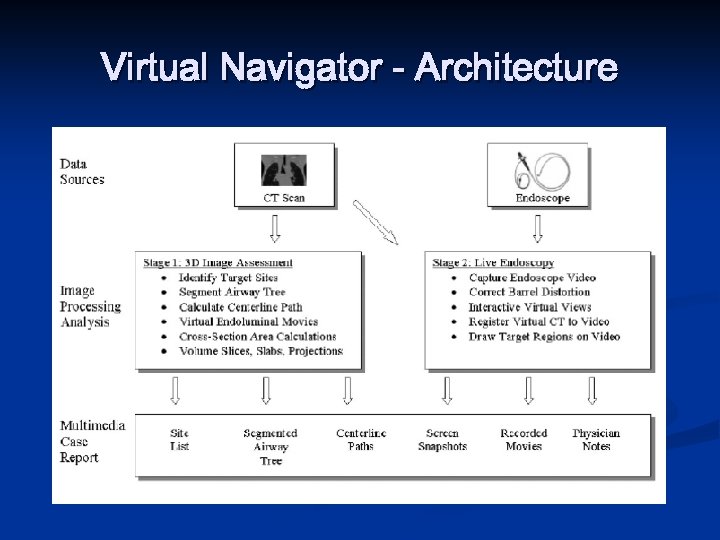
Virtual Navigator - Architecture

üAPPLICATIONS

Virtual colonoscopy v v v simplification of the colonic surface by decimation thinning of the decimated colon to create a preliminary centerline selection of equally spaced points on the preliminary centerline v grouping neighboring points v mapping them back to rings in the original colon Gheorghe Iordanescu, Ph. D, Ronald M. Summers, MD, Ph. D

Virtual colonoscopy start ü ü 1. decimation 2. thinning 3. modeling 4. remapping 5. Centerline computation 6. Final remapping Start: The starting point is the original colon surface (SOC), produced from the CTC images using a region growing segmentation and isosurface extraction. The threshold for the isosurface extraction is a specific Hounsfield unit (HU). The “marching cubes” algorithm was used to extract the isosurface. The surface is composed of many small triangles, which are described by their vertices and edges. Decimation: The SOC is simplified using decimation to minimize the number of operations performed in subsequent steps. Decimation keeps the general appearance and topology of the colon but reduce the number of vertices in region of the surface with low curvature. The result of this step is the decimated colon surface (SDC). Gheorghe Iordanescu, Ph. D, Ronald M. Summers, MD, Ph. D
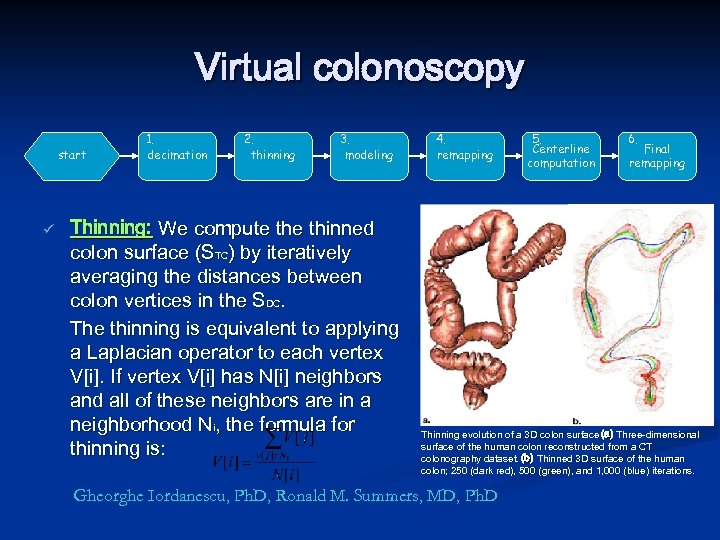
Virtual colonoscopy start ü 1. decimation 2. thinning 3. modeling Thinning: We compute thinned colon surface (STC) by iteratively averaging the distances between colon vertices in the SDC. The thinning is equivalent to applying a Laplacian operator to each vertex V[i]. If vertex V[i] has N[i] neighbors and all of these neighbors are in a neighborhood Ni, the formula for thinning is: 4. remapping 5. Centerline computation 6. Final remapping Thinning evolution of a 3 D colon surface (a) Three-dimensional surface of the human colon reconstructed from a CT colonography dataset. (b) Thinned 3 D surface of the human colon; 250 (dark red), 500 (green), and 1, 000 (blue) iterations. Gheorghe Iordanescu, Ph. D, Ronald M. Summers, MD, Ph. D
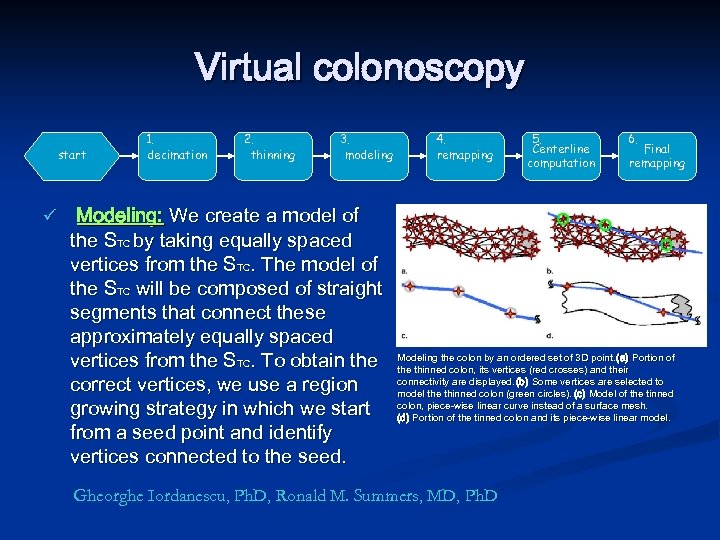
Virtual colonoscopy start ü 1. decimation 2. thinning 3. modeling Modeling: We create a model of the STC by taking equally spaced vertices from the STC. The model of the STC will be composed of straight segments that connect these approximately equally spaced vertices from the STC. To obtain the correct vertices, we use a region growing strategy in which we start from a seed point and identify vertices connected to the seed. 4. remapping 5. Centerline computation 6. Final remapping Modeling the colon by an ordered set of 3 D point. (a) Portion of the thinned colon, its vertices (red crosses) and their connectivity are displayed. (b) Some vertices are selected to model the thinned colon (green circles). (c) Model of the tinned colon, piece-wise linear curve instead of a surface mesh. (d) Portion of the tinned colon and its piece-wise linear model. Gheorghe Iordanescu, Ph. D, Ronald M. Summers, MD, Ph. D
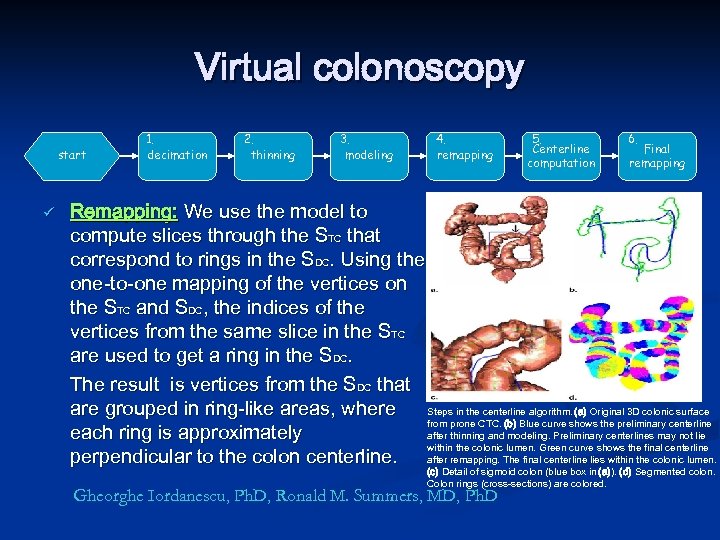
Virtual colonoscopy start ü 1. decimation 2. thinning 3. modeling 4. remapping 5. Centerline computation 6. Final remapping Remapping: We use the model to compute slices through the STC that correspond to rings in the SDC. Using the one-to-one mapping of the vertices on the STC and SDC, the indices of the vertices from the same slice in the STC are used to get a ring in the SDC. The result is vertices from the SDC that are grouped in ring-like areas, where Steps in the centerline algorithm. (a) Original 3 D colonic surface from prone CTC. (b) Blue curve shows the preliminary centerline each ring is approximately after thinning and modeling. Preliminary centerlines may not lie within the colonic lumen. Green curve shows the final centerline perpendicular to the colon centerline. after remapping. The final centerline lies within the colonic lumen. (c) Detail of sigmoid colon (blue box in (a)). (d) Segmented colon. Colon rings (cross-sections) are colored. Gheorghe Iordanescu, Ph. D, Ronald M. Summers, MD, Ph. D
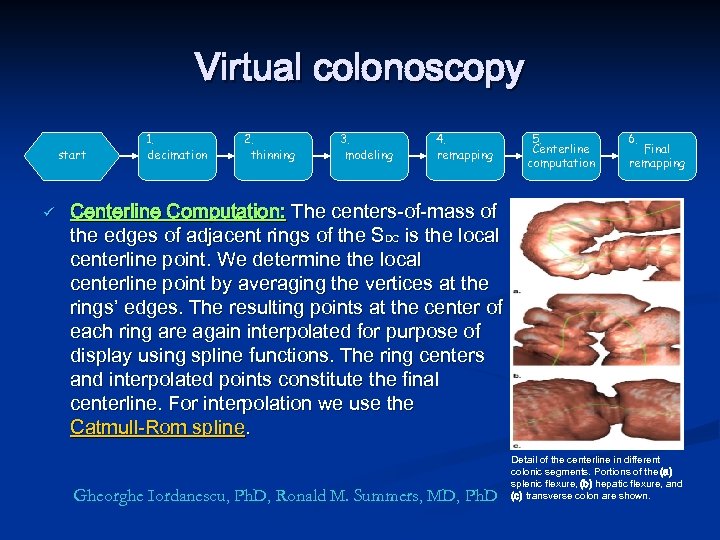
Virtual colonoscopy start ü 1. decimation 2. thinning 3. modeling 4. remapping 5. Centerline computation 6. Final remapping Centerline Computation: The centers-of-mass of the edges of adjacent rings of the SDC is the local centerline point. We determine the local centerline point by averaging the vertices at the rings’ edges. The resulting points at the center of each ring are again interpolated for purpose of display using spline functions. The ring centers and interpolated points constitute the final centerline. For interpolation we use the Catmull-Rom spline. Gheorghe Iordanescu, Ph. D, Ronald M. Summers, MD, Ph. D Detail of the centerline in different colonic segments. Portions of the (a) splenic flexure, (b) hepatic flexure, and (c) transverse colon are shown.

Virtual colonoscopy start ü 1. decimation 2. thinning 3. modeling 4. remapping 5. Centerline computation 6. Final remapping Mapping the SDC to the SOC: A second mapper associates vertices in the SDC with the vertices in the SOC based on minimum distance criterion between the vertices of the two surfaces. Based on the correspondence of the vertices on the SDC and SOC we can segment the SOC and split the surface into rings. To limit the search space and improve computational efficiency in performing this second mapping , a process called “vertex classification” is performed, vertices in the SDC and SOC are grouped into classes according to their spatial coordinates. Because only vertices in neighboring classes need to be searched, there is a substantial performance improvement. Gheorghe Iordanescu, Ph. D, Ronald M. Summers, MD, Ph. D
Virtual colonoscopy

Virtual Endoscopy (based on potential fields) O O O The idea is to utilize a hierarchical analysis of attractors to determine principal attractors We combine potentials derived from the distance between source and target positions and from the distance to the colon surface to guide path search process, the paths far away from the colon wall and in the direction of target position Advantages: O O O Eliminating small-undesired branches during the attractor analysis. Warranty of connectivity between start and target points. Search of paths just between principal attractors and do not waste time in connecting the small attractors. Rui C. H. Chiou, Arie E. Kaufman, Zhengrong Liang, Lichan Hong and Miranda Achniotou

Virtual Endoscopy (based on potential fields) v Calculate distance from surface and target v Detect attractors v Analyze hierarchical attractors v v Analyze attractors according to their contribution to principal skeleton Calculate distance from next consecutive principal attractor v v v The idea is to take the most powerful attractor and scan its influence zone by 3 D distance region growing The process repeats for the next most powerful attractor until the source target principal attractors are found Search paths between principal attractors Rui C. H. Chiou, Arie E. Kaufman, Zhengrong Liang, Lichan Hong and Miranda Achniotou

Virtual Endoscopy
Virtual Bronchoscopy ü ü VB is a computer-based approach for navigating virtually through airways captured in a 3 -D MDCT image VB 3 -D image analysis: ü ü ü Guidance of bronchoscopy Human lung-cancer assessment Planning and guiding bronchoscopic biopsies Quantitative airway analysis –noninvasively. Smooth virtual navigation A suitable method must: ü ü ü Provide a detailed, smooth structure of the airway tree’s central axes Require little human interaction Function over a wide range of conditions as observed in typical lungcancer patients A. P. Kiraly, J. P. Helferty, E. A. Hoffman, G. Mc. Lennan, and W. E. Higgins
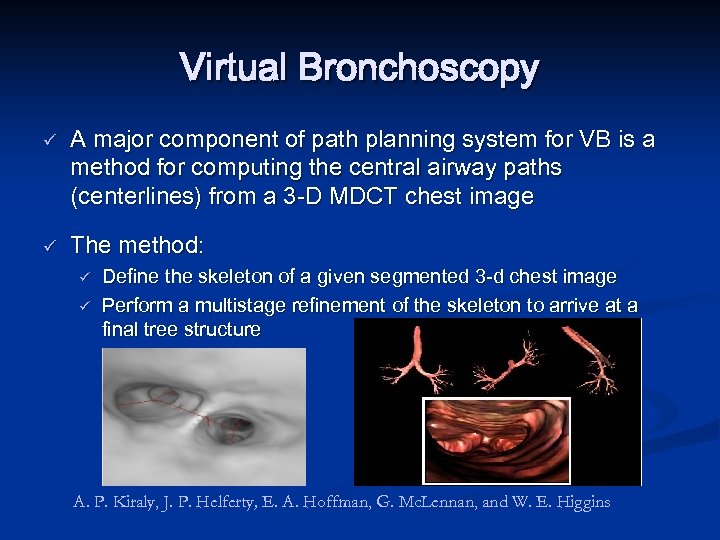
Virtual Bronchoscopy ü ü A major component of path planning system for VB is a method for computing the central airway paths (centerlines) from a 3 -D MDCT chest image The method: ü ü Define the skeleton of a given segmented 3 -d chest image Perform a multistage refinement of the skeleton to arrive at a final tree structure A. P. Kiraly, J. P. Helferty, E. A. Hoffman, G. Mc. Lennan, and W. E. Higgins
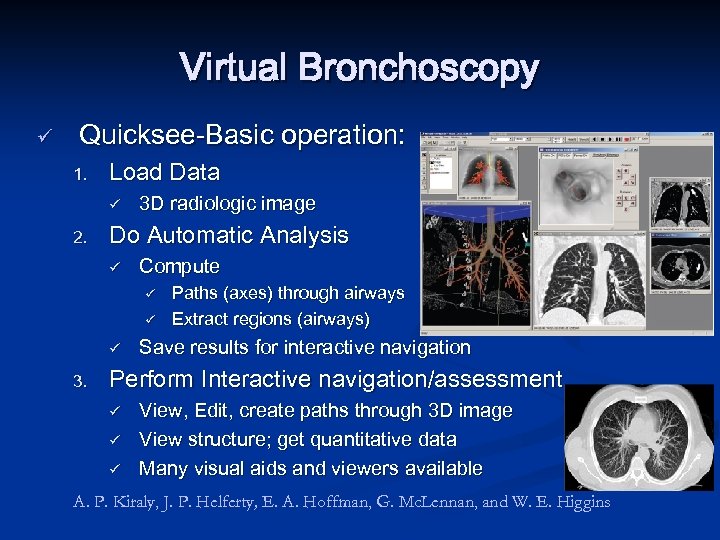
Virtual Bronchoscopy ü Quicksee-Basic operation: 1. Load Data ü 2. 3 D radiologic image Do Automatic Analysis ü Compute ü ü ü 3. Paths (axes) through airways Extract regions (airways) Save results for interactive navigation Perform Interactive navigation/assessment ü ü ü View, Edit, create paths through 3 D image View structure; get quantitative data Many visual aids and viewers available A. P. Kiraly, J. P. Helferty, E. A. Hoffman, G. Mc. Lennan, and W. E. Higgins
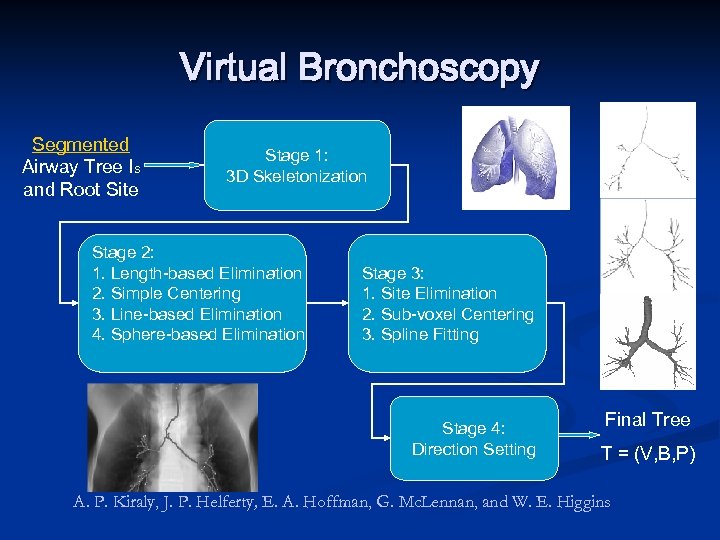
Virtual Bronchoscopy Segmented Airway Tree IS and Root Site Stage 1: 3 D Skeletonization Stage 2: 1. Length-based Elimination 2. Simple Centering 3. Line-based Elimination 4. Sphere-based Elimination Stage 3: 1. Site Elimination 2. Sub-voxel Centering 3. Spline Fitting Stage 4: Direction Setting Final Tree T = (V, B, P) A. P. Kiraly, J. P. Helferty, E. A. Hoffman, G. Mc. Lennan, and W. E. Higgins
Virtual Bronchoscopy A. P. Kiraly, J. P. Helferty, E. A. Hoffman, G. Mc. Lennan, and W. E. Higgins

OUR WORK n Goals: n n The aim of our work is to build trajectories for virtual endoscopy inside 3 D medical images, using the most automatic way. Virtual endoscopy results are shown in various anatomical regions (bronchi, colon, brain vessels, arteries) with different 3 D imaging protocols (CT, MR). In my thesis, an automatic centerline determination algorithm for three dimensional virtual bronchoscopy CT image will be present. We try that our method: n Be faster n Needs less interaction n Be more robust and reproducible
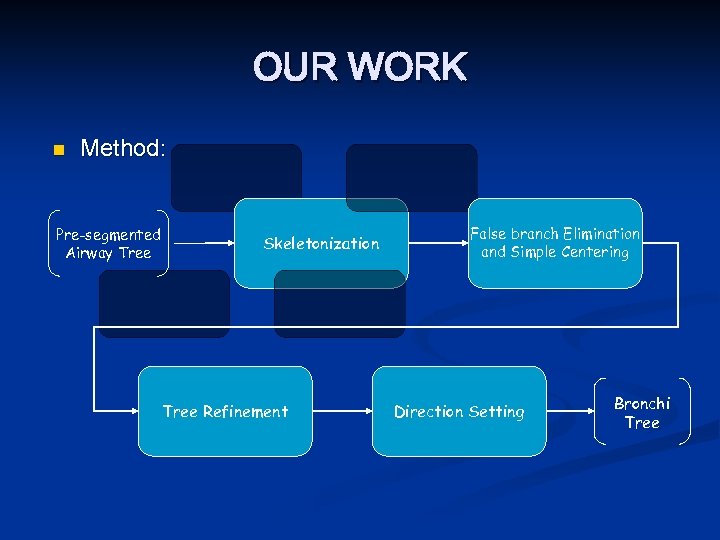
OUR WORK n Method: Pre-segmented Airway Tree Skeletonization Tree Refinement False branch Elimination and Simple Centering Direction Setting Bronchi Tree
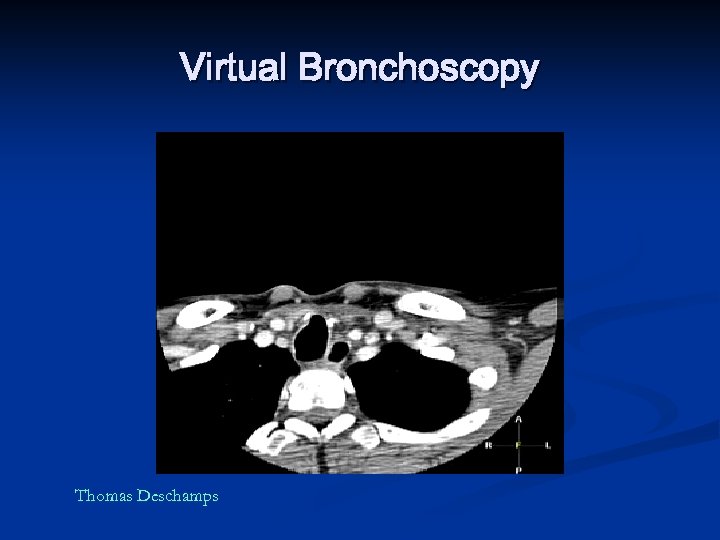
Virtual Bronchoscopy Thomas Deschamps
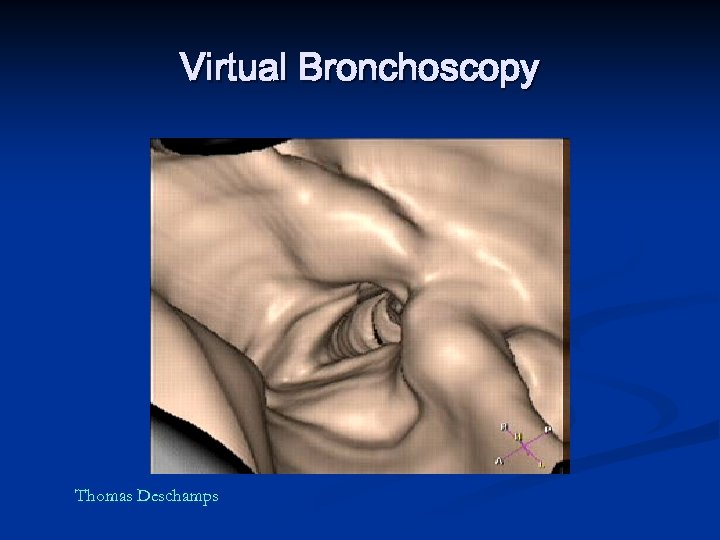
Virtual Bronchoscopy Thomas Deschamps

Discussion Questions …. Suggestions …. Comments …. Ideas …. ? mrnegahdar@razi. tums. ac. ir mrnus@yahoo. com
a6bdbec2221e4450272c42c92cac9db6.ppt