e01accc9951ce9b75342249490d07605.ppt
- Количество слайдов: 47
 Path Disruption Games (Cooperative Game Theory meets Network Security) Yoram Bachrach, Ely Porat Microsoft Research Cambridge
Path Disruption Games (Cooperative Game Theory meets Network Security) Yoram Bachrach, Ely Porat Microsoft Research Cambridge
 Agenda Motivating Examples Cooperative Game Theory Path Disruption Games
Agenda Motivating Examples Cooperative Game Theory Path Disruption Games
 Hospitals and Cost Sharing • Three private hospitals need an X-Ray machine Machine Cost Serving Cheap £ 5 M 2 hospitals Expensive £ 9 M 3 hospitals • Optimal solution – Two cheap machines cost £ 10 M – Buy the £ 9 M machine share it • Private sector problem – Private hospitals negotiate • What to buy • How to share the costs
Hospitals and Cost Sharing • Three private hospitals need an X-Ray machine Machine Cost Serving Cheap £ 5 M 2 hospitals Expensive £ 9 M 3 hospitals • Optimal solution – Two cheap machines cost £ 10 M – Buy the £ 9 M machine share it • Private sector problem – Private hospitals negotiate • What to buy • How to share the costs
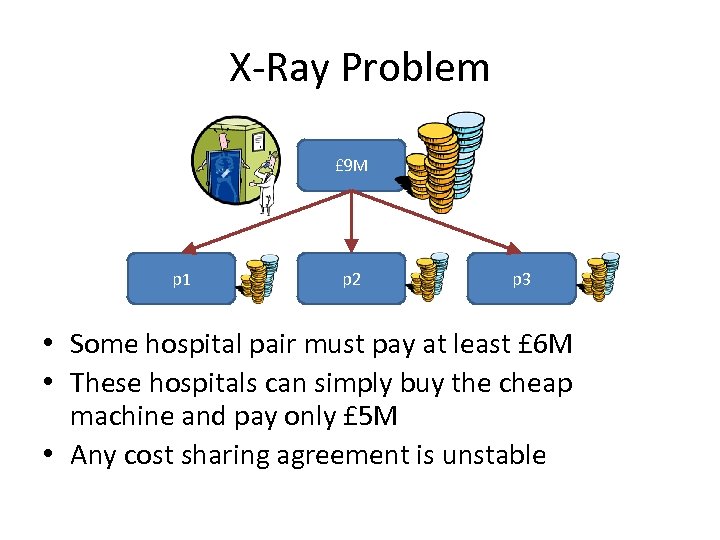 X-Ray Problem £ 9 M p 1 p 2 p 3 • Some hospital pair must pay at least £ 6 M • These hospitals can simply buy the cheap machine and pay only £ 5 M • Any cost sharing agreement is unstable
X-Ray Problem £ 9 M p 1 p 2 p 3 • Some hospital pair must pay at least £ 6 M • These hospitals can simply buy the cheap machine and pay only £ 5 M • Any cost sharing agreement is unstable
 Treasure Island • Jim, Billy and Smollett are looking for a buried treasure, worth a £ 1000 – Billy and Jim each have half of the map • Each half is useless on its own – Smollett has a ship that can sail to treasure island • Renting a ship from anyone else costs £ 800 – v(J)=v(B)=v(S)=v(J, S)=v(B, S)=£ 0 – v(J, B)=£ 200 – V(J, B, S)=£ 1000 • How should they split the gains?
Treasure Island • Jim, Billy and Smollett are looking for a buried treasure, worth a £ 1000 – Billy and Jim each have half of the map • Each half is useless on its own – Smollett has a ship that can sail to treasure island • Renting a ship from anyone else costs £ 800 – v(J)=v(B)=v(S)=v(J, S)=v(B, S)=£ 0 – v(J, B)=£ 200 – V(J, B, S)=£ 1000 • How should they split the gains?
 Treasure Island – Forming Coalitions £ 200 £ 1000
Treasure Island – Forming Coalitions £ 200 £ 1000
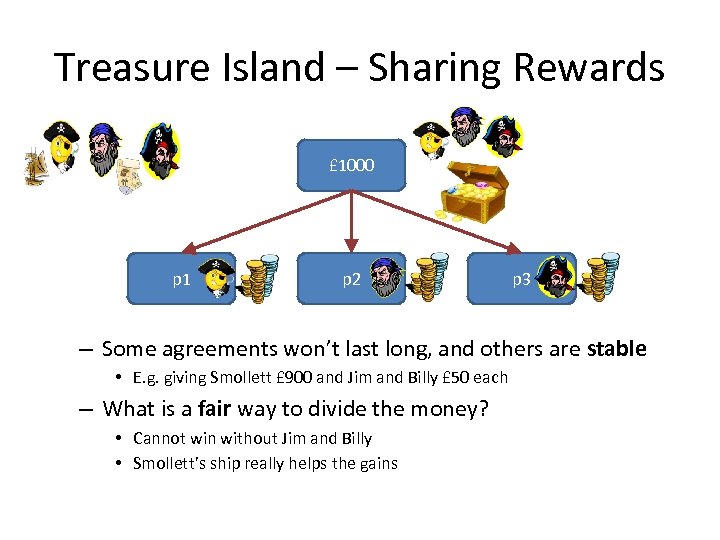 Treasure Island – Sharing Rewards £ 1000 p 1 p 2 p 3 – Some agreements won’t last long, and others are stable • E. g. giving Smollett £ 900 and Jim and Billy £ 50 each – What is a fair way to divide the money? • Cannot win without Jim and Billy • Smollett’s ship really helps the gains
Treasure Island – Sharing Rewards £ 1000 p 1 p 2 p 3 – Some agreements won’t last long, and others are stable • E. g. giving Smollett £ 900 and Jim and Billy £ 50 each – What is a fair way to divide the money? • Cannot win without Jim and Billy • Smollett’s ship really helps the gains
 UK Elections 2010: Budgets and Politics Conservatives Labour Lib-Dems 306 258 57 • No party had the required majority (326 seats) – Hung parliament • Second time since World War II – Previous time was 1974 • First coalition government to eventuate from elections – The Lib-Dems only had 57/650=8. 8% of seats • But large influence on policy • Other alternative for the conservatives – government with labour – Not very appealing to the conservatives…
UK Elections 2010: Budgets and Politics Conservatives Labour Lib-Dems 306 258 57 • No party had the required majority (326 seats) – Hung parliament • Second time since World War II – Previous time was 1974 • First coalition government to eventuate from elections – The Lib-Dems only had 57/650=8. 8% of seats • But large influence on policy • Other alternative for the conservatives – government with labour – Not very appealing to the conservatives…
 An Alternate Universe Conservatives Labour Liberals Democrats 306 28 29 258 • Would the Conservatives be more powerful or less powerful in this alternate universe? – Intuition: much more alternatives to choose from! • What determines the balance of power? – Suppose parties have to allocate a budget…
An Alternate Universe Conservatives Labour Liberals Democrats 306 28 29 258 • Would the Conservatives be more powerful or less powerful in this alternate universe? – Intuition: much more alternatives to choose from! • What determines the balance of power? – Suppose parties have to allocate a budget…
 Cooperative Games • Agents must cooperate to achieve their goals… • … but are still selfish – – Maximize their share of the rewards Obtain the outcome maximizing their utility Minimize their own cost Maximize their influence • What teams and agreements would form?
Cooperative Games • Agents must cooperate to achieve their goals… • … but are still selfish – – Maximize their share of the rewards Obtain the outcome maximizing their utility Minimize their own cost Maximize their influence • What teams and agreements would form?
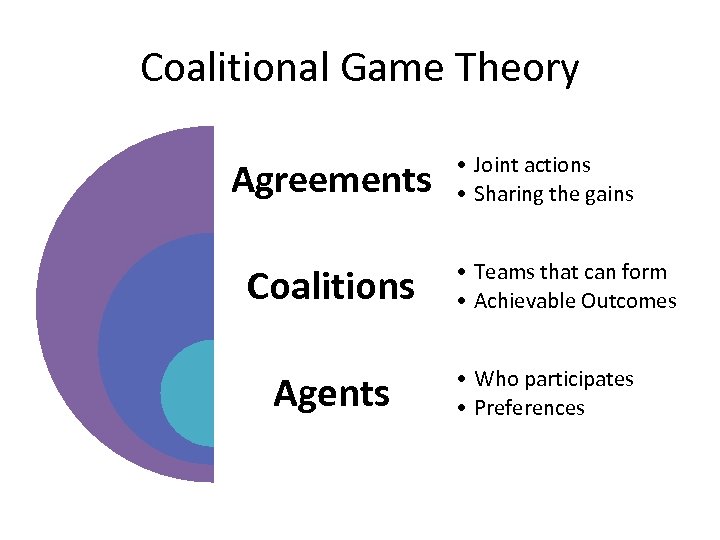 Coalitional Game Theory Agreements Coalitions Agents • Joint actions • Sharing the gains • Teams that can form • Achievable Outcomes • Who participates • Preferences
Coalitional Game Theory Agreements Coalitions Agents • Joint actions • Sharing the gains • Teams that can form • Achievable Outcomes • Who participates • Preferences
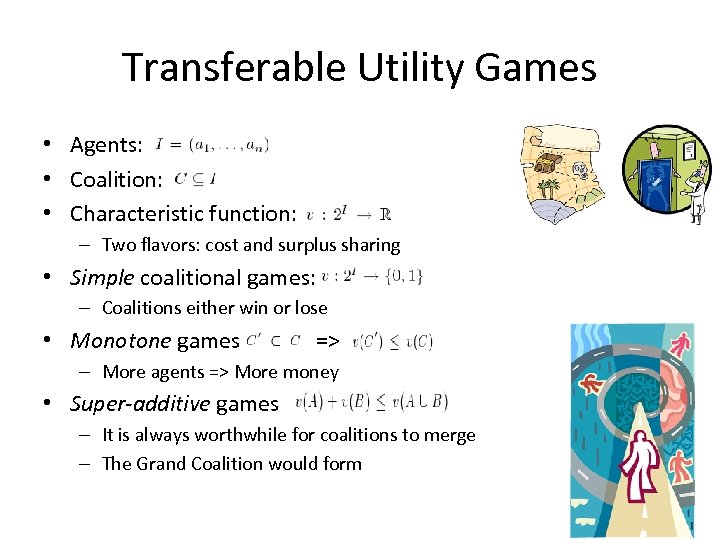 Transferable Utility Games • Agents: • Coalition: • Characteristic function: – Two flavors: cost and surplus sharing • Simple coalitional games: – Coalitions either win or lose • Monotone games => – More agents => More money • Super-additive games – It is always worthwhile for coalitions to merge – The Grand Coalition would form
Transferable Utility Games • Agents: • Coalition: • Characteristic function: – Two flavors: cost and surplus sharing • Simple coalitional games: – Coalitions either win or lose • Monotone games => – More agents => More money • Super-additive games – It is always worthwhile for coalitions to merge – The Grand Coalition would form
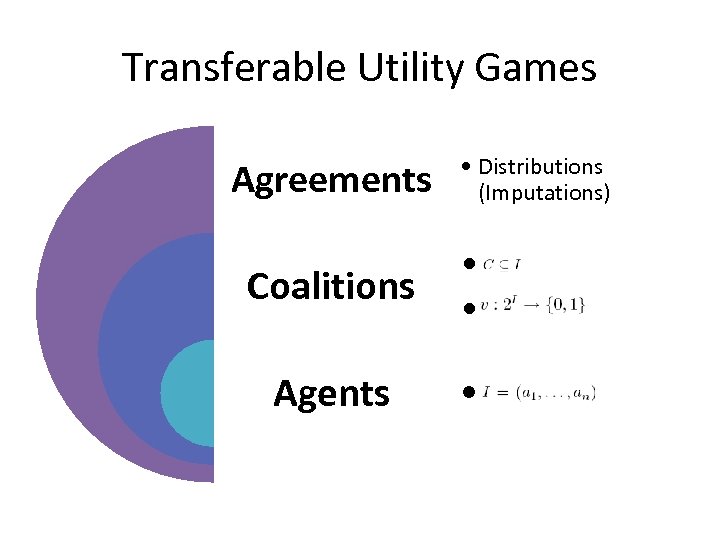 Transferable Utility Games Agreements • Distributions (Imputations) Coalitions • • Agents •
Transferable Utility Games Agreements • Distributions (Imputations) Coalitions • • Agents •
 Agent properties • Veto agent – Can’t win without the agent (simple games) – Can’t generate any value without the agent (Non-simple games) • Dummy agent – Never contributes to any coalition • Equivalent agents , => – Contribute equally to any coalition that contains neither of them • Critical agent for a coalition – The coalition wins with the agent, but loses without the agent
Agent properties • Veto agent – Can’t win without the agent (simple games) – Can’t generate any value without the agent (Non-simple games) • Dummy agent – Never contributes to any coalition • Equivalent agents , => – Contribute equally to any coalition that contains neither of them • Critical agent for a coalition – The coalition wins with the agent, but loses without the agent
 Payoffs • Imputations define how the total utility is distributed • A payoff vector such that • Individual rationality – Otherwise, an agent can do better alone • The payoff of a coalition C is • A coalition C is blocking if p(C) < v(C)
Payoffs • Imputations define how the total utility is distributed • A payoff vector such that • Individual rationality – Otherwise, an agent can do better alone • The payoff of a coalition C is • A coalition C is blocking if p(C) < v(C)
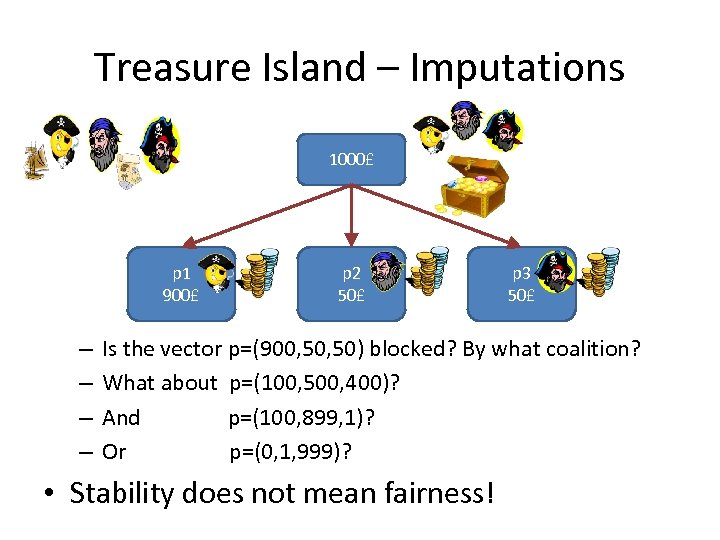 Treasure Island – Imputations 1000£ p 1 900£ – – p 2 50£ p 3 50£ Is the vector p=(900, 50) blocked? By what coalition? What about p=(100, 500, 400)? And p=(100, 899, 1)? Or p=(0, 1, 999)? • Stability does not mean fairness!
Treasure Island – Imputations 1000£ p 1 900£ – – p 2 50£ p 3 50£ Is the vector p=(900, 50) blocked? By what coalition? What about p=(100, 500, 400)? And p=(100, 899, 1)? Or p=(0, 1, 999)? • Stability does not mean fairness!
 The Core (Stability) • All imputations that are not blocked by any coalition • For any coalition C, p(C) ≥ v(C) – For cost sharing games, the inequality is reversed • No coalition is incentived to defect from the grand coalition • Gillies (1953) and von Neumann & Morgenstein (1947)
The Core (Stability) • All imputations that are not blocked by any coalition • For any coalition C, p(C) ≥ v(C) – For cost sharing games, the inequality is reversed • No coalition is incentived to defect from the grand coalition • Gillies (1953) and von Neumann & Morgenstein (1947)
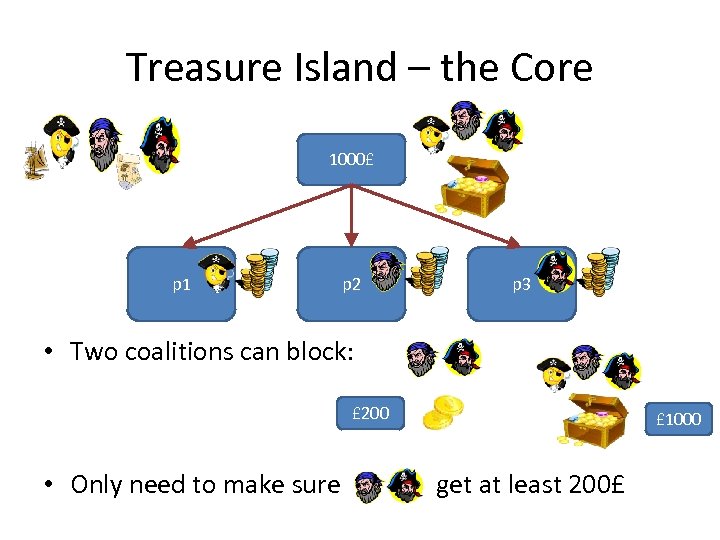 Treasure Island – the Core 1000£ p 1 p 2 p 3 • Two coalitions can block: £ 200 • Only need to make sure £ 1000 get at least 200£
Treasure Island – the Core 1000£ p 1 p 2 p 3 • Two coalitions can block: £ 200 • Only need to make sure £ 1000 get at least 200£
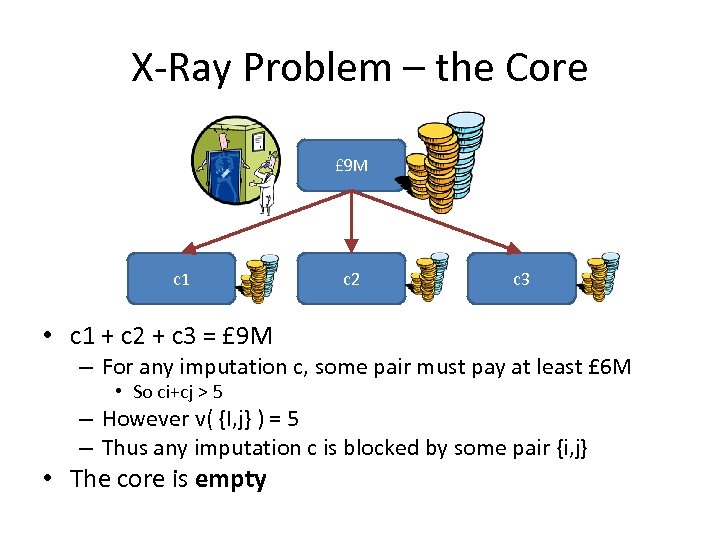 X-Ray Problem – the Core £ 9 M c 1 c 2 c 3 • c 1 + c 2 + c 3 = £ 9 M – For any imputation c, some pair must pay at least £ 6 M • So ci+cj > 5 – However v( {I, j} ) = 5 – Thus any imputation c is blocked by some pair {i, j} • The core is empty
X-Ray Problem – the Core £ 9 M c 1 c 2 c 3 • c 1 + c 2 + c 3 = £ 9 M – For any imputation c, some pair must pay at least £ 6 M • So ci+cj > 5 – However v( {I, j} ) = 5 – Thus any imputation c is blocked by some pair {i, j} • The core is empty
 Weighted Voting Games (WVG) • • • Set of agents Each agent has a weight A game has a quota A coalition C wins if A simple game (coalitions either win or lose)
Weighted Voting Games (WVG) • • • Set of agents Each agent has a weight A game has a quota A coalition C wins if A simple game (coalitions either win or lose)
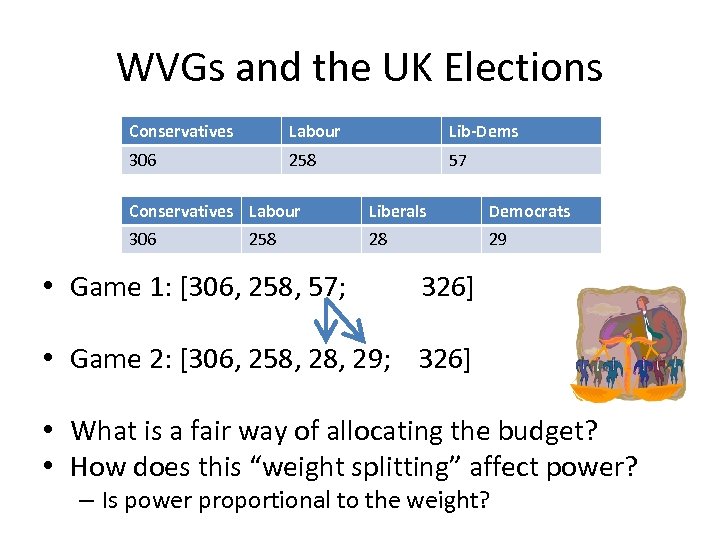 WVGs and the UK Elections Conservatives Labour Lib-Dems 306 258 57 Conservatives Labour Liberals Democrats 306 28 29 258 • Game 1: [306, 258, 57; 326] • Game 2: [306, 258, 29; 326] • What is a fair way of allocating the budget? • How does this “weight splitting” affect power? – Is power proportional to the weight?
WVGs and the UK Elections Conservatives Labour Lib-Dems 306 258 57 Conservatives Labour Liberals Democrats 306 28 29 258 • Game 1: [306, 258, 57; 326] • Game 2: [306, 258, 29; 326] • What is a fair way of allocating the budget? • How does this “weight splitting” affect power? – Is power proportional to the weight?
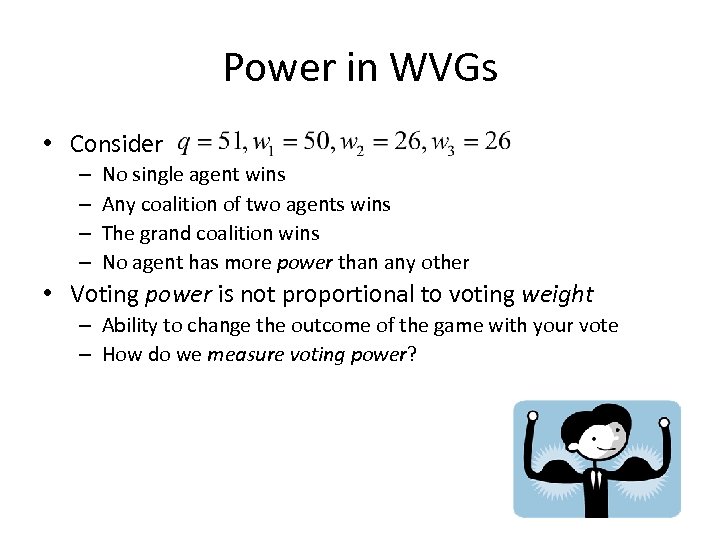 Power in WVGs • Consider – – No single agent wins Any coalition of two agents wins The grand coalition wins No agent has more power than any other • Voting power is not proportional to voting weight – Ability to change the outcome of the game with your vote – How do we measure voting power?
Power in WVGs • Consider – – No single agent wins Any coalition of two agents wins The grand coalition wins No agent has more power than any other • Voting power is not proportional to voting weight – Ability to change the outcome of the game with your vote – How do we measure voting power?
 Fairness • Return of the Pirates Treasure Island (1000£) Treasure Cave (2000£)
Fairness • Return of the Pirates Treasure Island (1000£) Treasure Cave (2000£)
 Fairness Requirements • A solution concept maps a game (characteristic function) to an imputation for that game • Efficiency Axiom: • Dummy Axiom: dummy agents get nothing • Symmetry Axiom: Equivalent agents get the same • Additivity axiom: – If a game is composed of two sub-games • (v+w)(C) = v(C)+w(C) • E. g. playing both treasure island treasure cave – Then an agent’s payoff in v+w is the sum of her payoffs in v and in w • Is there a solution concept that fulfills all these fairness axioms?
Fairness Requirements • A solution concept maps a game (characteristic function) to an imputation for that game • Efficiency Axiom: • Dummy Axiom: dummy agents get nothing • Symmetry Axiom: Equivalent agents get the same • Additivity axiom: – If a game is composed of two sub-games • (v+w)(C) = v(C)+w(C) • E. g. playing both treasure island treasure cave – Then an agent’s payoff in v+w is the sum of her payoffs in v and in w • Is there a solution concept that fulfills all these fairness axioms?
 Marginal Contribution • Treasure island • The coalition has a value of 0£ – No full map • The coalition has a value of 1000£ • Agent has a marginal contribution of 1000£-0£=10000£ to coalition
Marginal Contribution • Treasure island • The coalition has a value of 0£ – No full map • The coalition has a value of 1000£ • Agent has a marginal contribution of 1000£-0£=10000£ to coalition
 Marginal Contribution • Treasure island • The coalition has a value of 200£ – Full map, no ship • The coalition has a value of 1000£ • Agent has a marginal contribution of 1000£-200£=800£ to coalition
Marginal Contribution • Treasure island • The coalition has a value of 200£ – Full map, no ship • The coalition has a value of 1000£ • Agent has a marginal contribution of 1000£-200£=800£ to coalition
 The Shapley Value: Fairness • Given an ordering of the agents in I, denotes the set of agents that appear before i in • The Shapley value is an agent’s marginal contribution to its predecessors, averaged across all permutations • The only solution concepts that fulfills all of the previously defined fairness axioms • Can also be used to measure power
The Shapley Value: Fairness • Given an ordering of the agents in I, denotes the set of agents that appear before i in • The Shapley value is an agent’s marginal contribution to its predecessors, averaged across all permutations • The only solution concepts that fulfills all of the previously defined fairness axioms • Can also be used to measure power
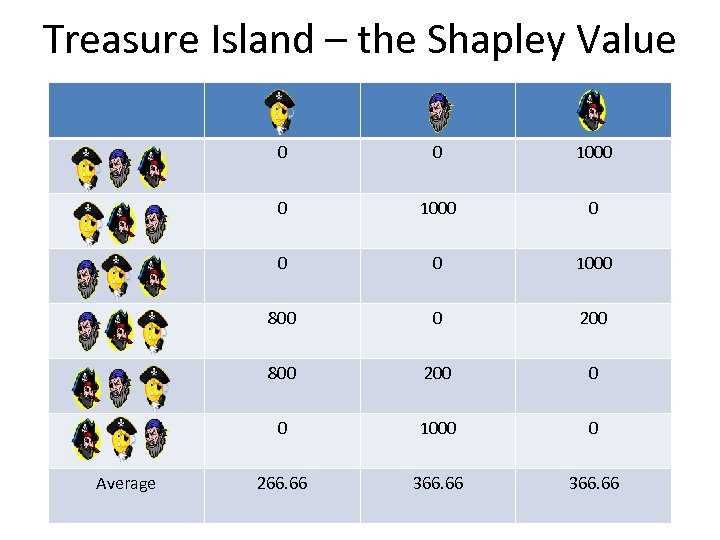 Treasure Island – the Shapley Value 0 1000 0 0 0 1000 800 0 200 800 200 0 0 Average 0 1000 0 266. 66 366. 66
Treasure Island – the Shapley Value 0 1000 0 0 0 1000 800 0 200 800 200 0 0 Average 0 1000 0 266. 66 366. 66
 Power Indices • Power in weighted voting games can be computed using the Shapley value – WVGs are simple games • The Shapely value measures the proportion of coalitions where an agent is critical • Each permutation has exactly one critical agent • Simple generative model • Are there alternative models or power indices?
Power Indices • Power in weighted voting games can be computed using the Shapley value – WVGs are simple games • The Shapely value measures the proportion of coalitions where an agent is critical • Each permutation has exactly one critical agent • Simple generative model • Are there alternative models or power indices?
 Power in the UK Elections Conservatives Labour Lib-Dems 306 258 57 66. 66% 16. 66% Conservatives Labour Liberals Democrats 306 258 28 29 75% 8. 33% • Game 1: [306, 258, 57; 326] • Game 2: [306, 258, 29; 326] • Split makes the labour less powerful – But the power goes to the conservatives… – … not the Lib-Dems
Power in the UK Elections Conservatives Labour Lib-Dems 306 258 57 66. 66% 16. 66% Conservatives Labour Liberals Democrats 306 258 28 29 75% 8. 33% • Game 1: [306, 258, 57; 326] • Game 2: [306, 258, 29; 326] • Split makes the labour less powerful – But the power goes to the conservatives… – … not the Lib-Dems
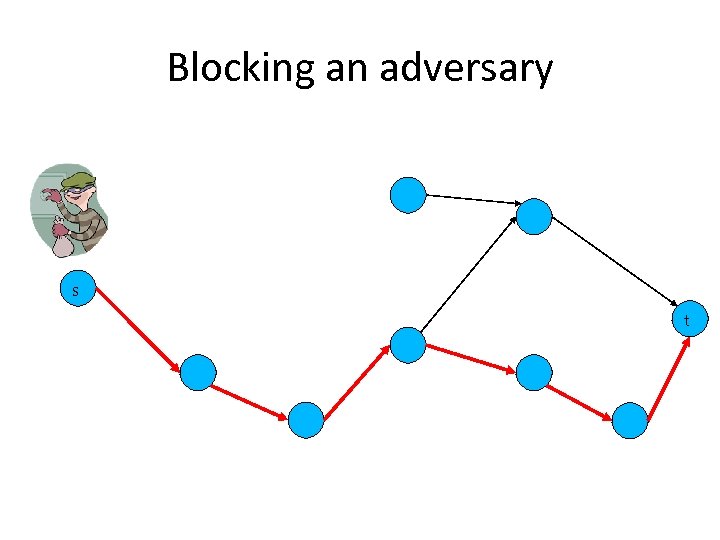
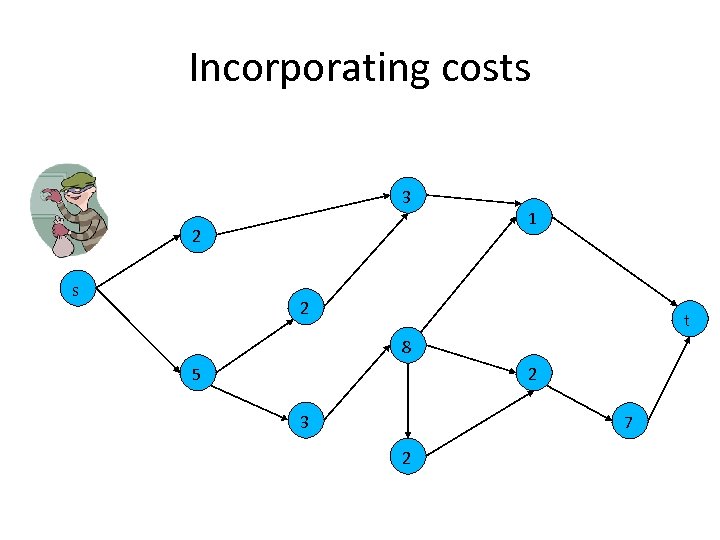
 Security in Networks • Physical network security – Placing checkpoints – Locations for routine checks • Network security – Protecting servers and links from attacks • Various costs for different nodes and links – How easy it is to deploy a check point – Performance degradation for protected servers • How should the budget be spent on security resources?
Security in Networks • Physical network security – Placing checkpoints – Locations for routine checks • Network security – Protecting servers and links from attacks • Various costs for different nodes and links – How easy it is to deploy a check point – Performance degradation for protected servers • How should the budget be spent on security resources?
 Blocking an adversary s t
Blocking an adversary s t
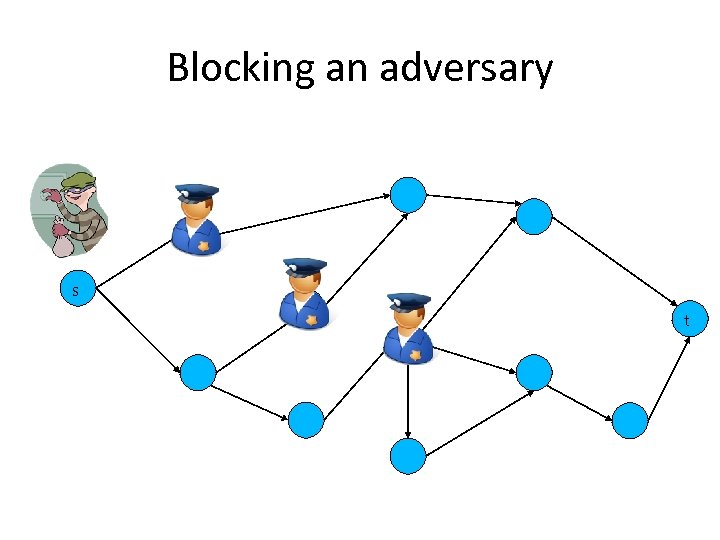 Blocking an adversary s t
Blocking an adversary s t
 Blocking an adversary s t
Blocking an adversary s t
 Blocking an adversary s t
Blocking an adversary s t
 Blocking an adversary s t
Blocking an adversary s t
 Blocking an adversary s t
Blocking an adversary s t
 Blocking an adversary s t
Blocking an adversary s t
 Incorporating costs 3 2 s 1 2 t 8 5 2 3 7 2
Incorporating costs 3 2 s 1 2 t 8 5 2 3 7 2
 Incorporating costs 3 2 s 1 2 t 8 5 2 3 7 2
Incorporating costs 3 2 s 1 2 t 8 5 2 3 7 2
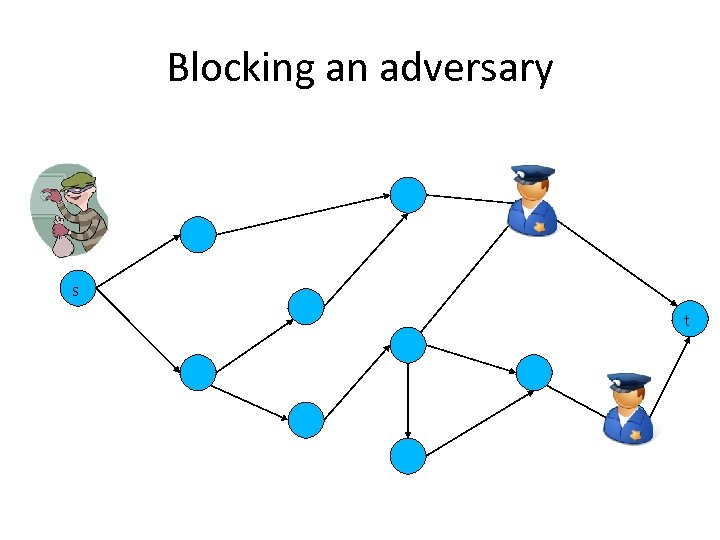
 Network Security Hotspots • Agents must for coalitions to successfully block the adversary – Obtain a certain reward or budget for achieving the task – How should this reward be shared between the agents • Stability – No subset of the coalition should have an incentive to form an alternative coalition • Fairness – Reflect the contribution of the each agent • Security resources are limited – Which node / link should be allocated these resources first? – Power indices allow finding such reliability hotspots
Network Security Hotspots • Agents must for coalitions to successfully block the adversary – Obtain a certain reward or budget for achieving the task – How should this reward be shared between the agents • Stability – No subset of the coalition should have an incentive to form an alternative coalition • Fairness – Reflect the contribution of the each agent • Security resources are limited – Which node / link should be allocated these resources first? – Power indices allow finding such reliability hotspots
 Path Disruption Games • Games played on a graph G=
Path Disruption Games • Games played on a graph G=
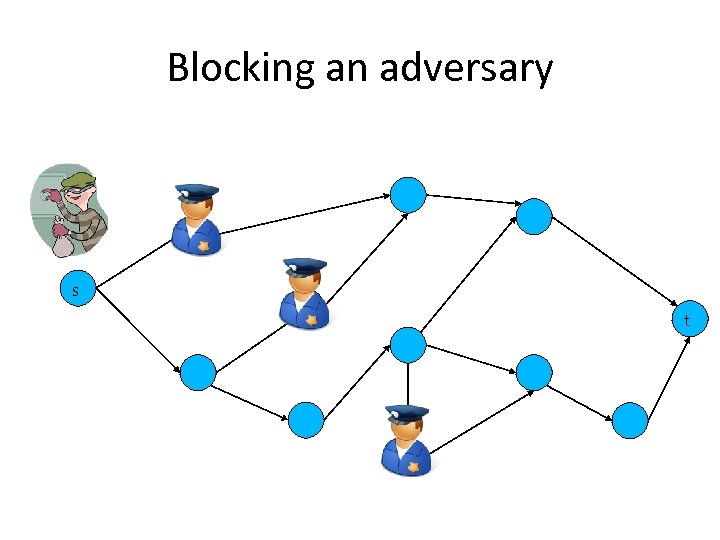
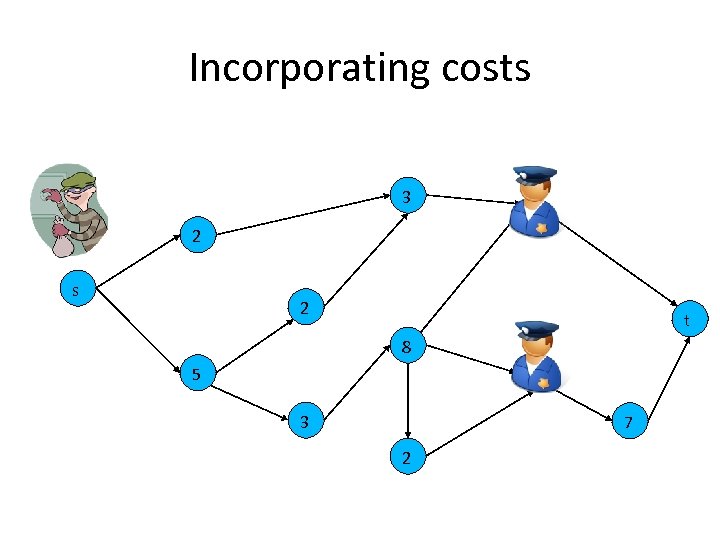
 Power and Security • Suppose all check points have equal probability, 50%, of blocking the adversary or not blocking – We have limited security resources – Which nodes should be protected first? • “Powerful” nodes are more critical – Suppose we can only choose one node where the adversary is blocked with 100% probability – The Banzhaf index of a node is the probability of stopping the adversary when: • This node blocks with probability 100% • All other nodes block with probability of 50%
Power and Security • Suppose all check points have equal probability, 50%, of blocking the adversary or not blocking – We have limited security resources – Which nodes should be protected first? • “Powerful” nodes are more critical – Suppose we can only choose one node where the adversary is blocked with 100% probability – The Banzhaf index of a node is the probability of stopping the adversary when: • This node blocks with probability 100% • All other nodes block with probability of 50%
 Stability in PDGs: the Core • Given a reward for blocking the adversary what check point coalitions would form? – We want the agents to work under enforceable contracts: • Which check points are used and • How to share the reward • The core constitutes a stable allocation – A distribution not in the core would break down the coalition structure – Unable to agree on a contract and infinite negotiation
Stability in PDGs: the Core • Given a reward for blocking the adversary what check point coalitions would form? – We want the agents to work under enforceable contracts: • Which check points are used and • How to share the reward • The core constitutes a stable allocation – A distribution not in the core would break down the coalition structure – Unable to agree on a contract and infinite negotiation
 Results • PDGs (several adversaries, no cost) – Can test for veto agents and compute the core in polynomial time – Computing the maximal excess for an imputation (payoff vector) is NP-complete • NP-hard to compute the least core – Testing for dummy agents is co. NP-Complete – Computing the Banzhaf index is #P-complete • But for trees it is computing in polynomial time
Results • PDGs (several adversaries, no cost) – Can test for veto agents and compute the core in polynomial time – Computing the maximal excess for an imputation (payoff vector) is NP-complete • NP-hard to compute the least core – Testing for dummy agents is co. NP-Complete – Computing the Banzhaf index is #P-complete • But for trees it is computing in polynomial time
 Results (cont. ) • Model with costs (PDGCs): – Computing the value of a coalition is NP-hard • Min cost vertex cut – Can do better for trees
Results (cont. ) • Model with costs (PDGCs): – Computing the value of a coalition is NP-hard • Min cost vertex cut – Can do better for trees
 Conclusion & Future Directions • Suggested a game theoretic model for network security based on blocking adversaries • Future work – Other solution concepts: power indices, nucleolus, kernel – More complex network security domains
Conclusion & Future Directions • Suggested a game theoretic model for network security based on blocking adversaries • Future work – Other solution concepts: power indices, nucleolus, kernel – More complex network security domains


