PASS WITH PEARSON Maths Achievement Standard 90152 Solve

PASS WITH PEARSON Maths Achievement Standard 90152 Solve right-angled triangle problems (1. 8) and Maths Achievement Standard 90153 Use geometric reasoning to solve problems (1. 9) Gwenda Hill How to use this CD and Legal Notices Press the ‘Esc’ key to exit at any time © Pearson Education New Zealand 2005 Start

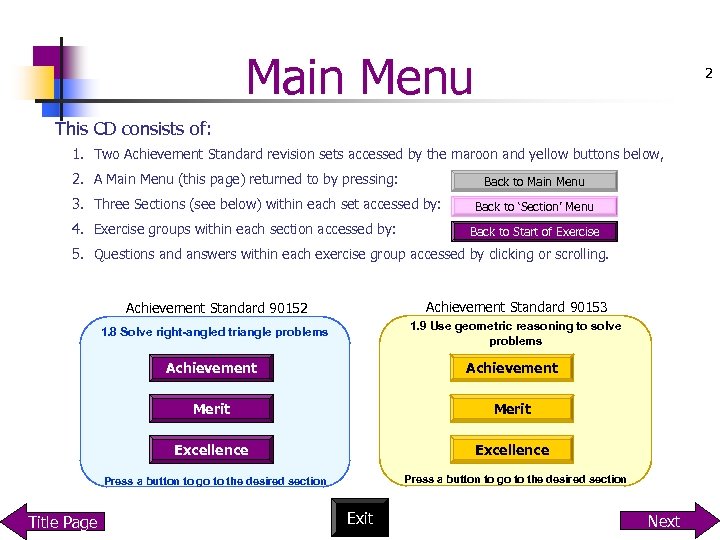Main Menu 2 This CD consists of: 1. Two Achievement Standard revision sets accessed by the maroon and yellow buttons below, 2. A Main Menu (this page) returned to by pressing: Back to Main Menu 3. Three Sections (see below) within each set accessed by: 4. Exercise groups within each section accessed by: Back to ‘Section’ Menu Back to Start of Exercise 5. Questions and answers within each exercise group accessed by clicking or scrolling. Achievement Standard 90152 Achievement Standard 90153 1. 8 Solve right-angled triangle problems 1. 9 Use geometric reasoning to solve problems Achievement Merit Excellence Press a button to go to the desired section Title Page Exit Next

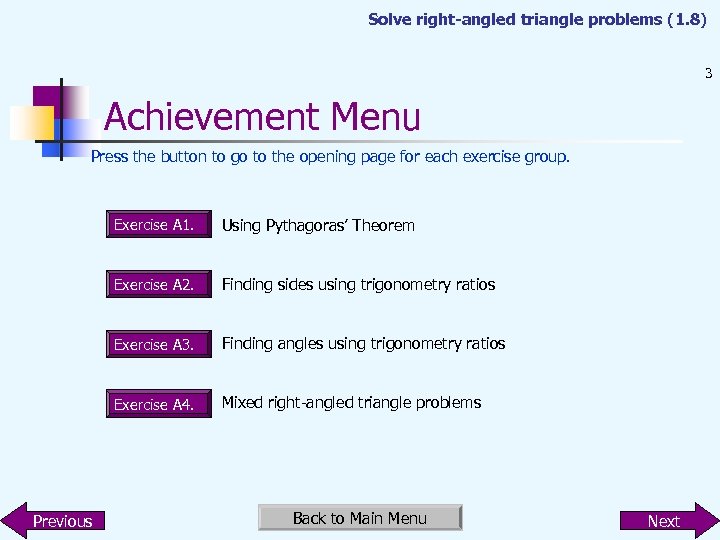Solve right-angled triangle problems (1. 8) 3 Achievement Menu Press the button to go to the opening page for each exercise group. Exercise A 1. Exercise A 2. Finding sides using trigonometry ratios Exercise A 3. Finding angles using trigonometry ratios Exercise A 4. Previous Using Pythagoras’ Theorem Mixed right-angled triangle problems Back to Main Menu Next

Solve right-angled triangle problems (1. 8) Exercise A 1 Solve right-angled triangle problems using Pythagoras’ Theorem Answer the four questions on page 4 of the book. Write down each question and answer and make sure you include your workings. Then click on the ‘next’ arrow to see the correct answers and the steps involved to achieving them. Previous Back to Achievement Menu Next

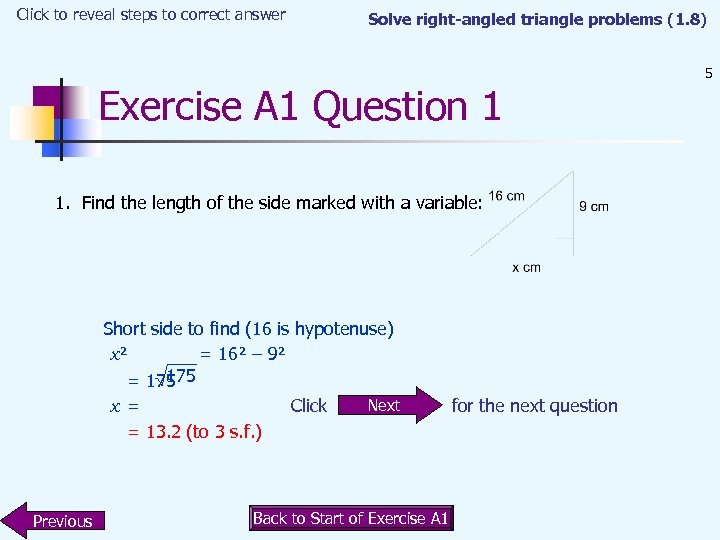Click to reveal steps to correct answer Solve right-angled triangle problems (1. 8) Exercise A 1 Question 1 1. Find the length of the side marked with a variable: Short side to find (16 is hypotenuse) x² = 16² – 9² 175 = 175 Next x = Click = 13. 2 (to 3 s. f. ) Previous Back to Start of Exercise A 1 for the next question 5

Click to reveal steps to correct answer Solve right-angled triangle problems (1. 8) Exercise A 1 Question 2 2. Find the length of the side marked with a variable: Long side to find (d is hypotenuse) d² = 23² + 9² = 593 d = Click Next for the next question = 24. 4 (to 3 s. f. ) Previous Back to Start of Exercise A 1 6

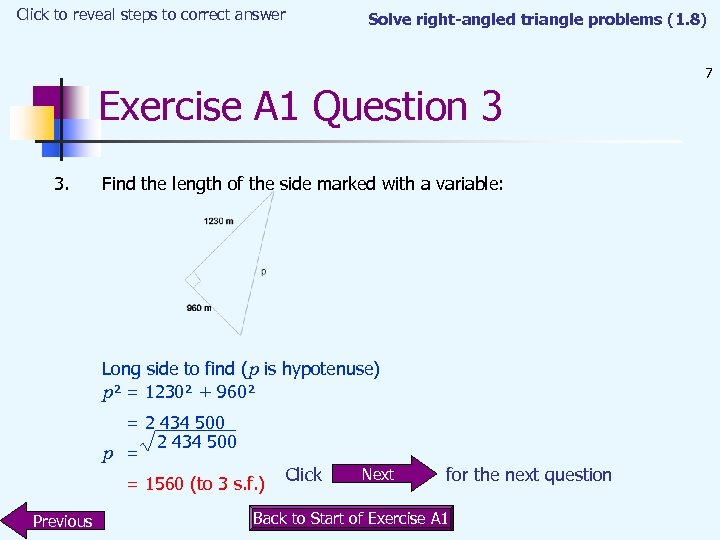Click to reveal steps to correct answer Solve right-angled triangle problems (1. 8) Exercise A 1 Question 3 3. Find the length of the side marked with a variable: Long side to find (p is hypotenuse) p² = 1230² + 960² = 2 434 500 p = = 1560 (to 3 s. f. ) Previous Click Next for the next question Back to Start of Exercise A 1 7

Click to reveal steps to correct answer Solve right-angled triangle problems (1. 8) Exercise A 1 Question 4 4. Find the length of the side marked with a variable: Short side to find (32. 7 is hypotenuse) x² = 32. 7² – 13. 2² = 895. 05 x = 895. 05 = 29. 9 (to 3 s. f. ) Click Previous Next for the next question Back to Start of Exercise A 1 8

Solve right-angled triangle problems (1. 8) Exercise A 2 Solve right-angled triangle problems finding sides using trigonometry ratios Answer the four questions on page 8 of the book. Write down each question and answer and make sure you include your workings. Then click on the ‘next’ arrow to see the correct answers and the steps involved to achieving them. Previous Back to Achievement Menu Next

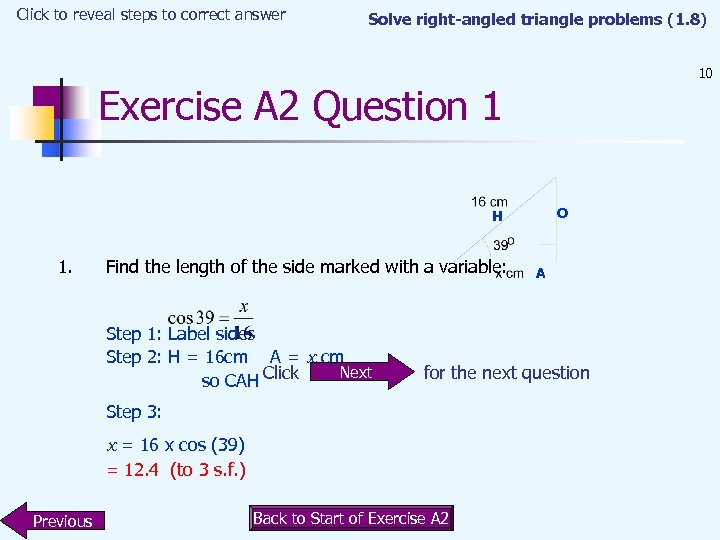Click to reveal steps to correct answer Solve right-angled triangle problems (1. 8) 10 Exercise A 2 Question 1 O H 1. Find the length of the side marked with a variable: Step 1: Label sides Step 2: H = 16 cm A = x cm Next so CAH Click for the next question Step 3: x = 16 x cos (39) = 12. 4 (to 3 s. f. ) Previous A Back to Start of Exercise A 2

Click to reveal steps to correct answer Solve right-angled triangle problems (1. 8) Exercise A 2 Question 2 2. Find the length of the side marked with. Aa variable: O H Step 1: Label sides Step 2: H = 8 mm O = c so SOH Step 3: c = sin(23) x 8 = 3. 1 mm (to 2 s. f. ) Previous Click Next Back to Start of Exercise A 2 for the next question 11

Click to reveal steps to correct answer Solve right-angled triangle problems (1. 8) 12 Exercise A 2 Question 3 A 3. Find the length of the side marked with a variable: H O Step 1: Label sides Step 2: A = 7 O = d Click so TOA Next for the next question Step 3: d = 7 x tan(43) = 6. 5 (to 2 s. f. ) Back to Start of Exercise A 2 Previous

Click to reveal steps to correct answer Solve right-angled triangle problems (1. 8) 13 Exercise A 2 Question 4 4. Find the length of the side marked with a variable: Step 1: Label sides Step 2: H = 50. 0 m Step 3: Previous y = sin(75) x 50. 0 = 48. 3 m (to 3 s. f. ) O H A O=y Click Next Back to Start of Exercise A 2 for the next question

Solve right-angled triangle problems (1. 8) Exercise A 3 Solve right-angled triangle problems finding angles using trigonometry ratios Answer the four questions on page 10 of the book. Write down each question and answer and make sure you include your workings. Then click on the ‘next’ arrow to see the correct answers and the steps involved to achieving them. Previous Back to Achievement Menu Next

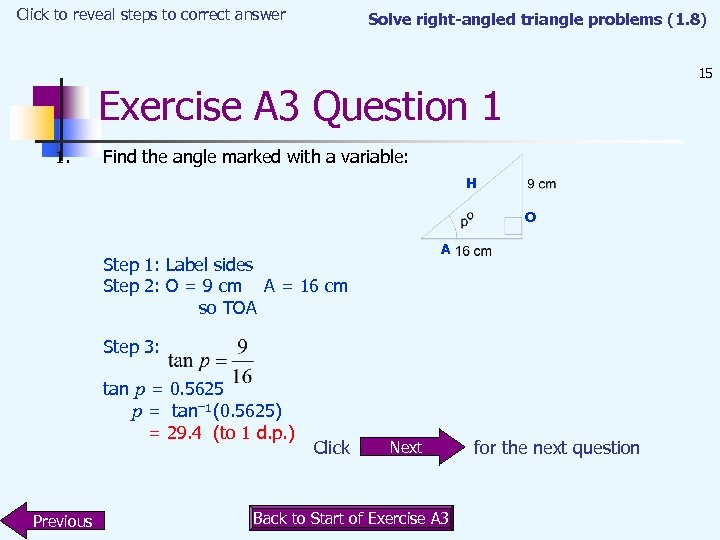Click to reveal steps to correct answer Solve right-angled triangle problems (1. 8) 15 Exercise A 3 Question 1 1. Find the angle marked with a variable: H O A Step 1: Label sides Step 2: O = 9 cm A = 16 cm so TOA Step 3: tan p = 0. 5625 p = tan–¹(0. 5625) = 29. 4 (to 1 d. p. ) Previous Click Next Back to Start of Exercise A 3 for the next question

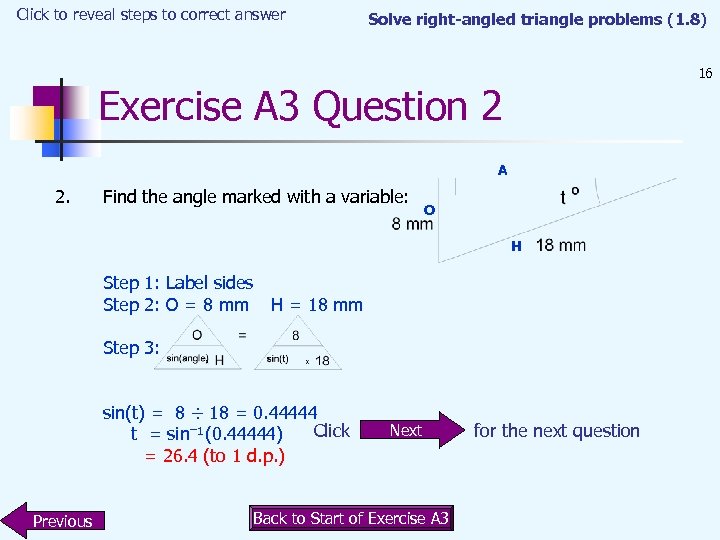Click to reveal steps to correct answer Solve right-angled triangle problems (1. 8) 16 Exercise A 3 Question 2 A 2. Find the angle marked with a variable: O H Step 1: Label sides Step 2: O = 8 mm H = 18 mm Step 3: sin(t) = 8 ÷ 18 = 0. 44444 Click t = sin–¹(0. 44444) = 26. 4 (to 1 d. p. ) Previous Next Back to Start of Exercise A 3 for the next question

Click to reveal steps to correct answer Solve right-angled triangle problems (1. 8) 17 Exercise A 3 Question 3 3. Find the angle marked with a variable: A Step 1: Label sides Step 2: O = 2. 8 H = 7 so SOH Step 3: H O sin(k) = 2. 8 ÷ 7 = 0. 4 k = sin–¹(0. 4) = 23. 6 (to 1 d. p. ) Click Previous Next for the next question Back to Start of Exercise A 3

Click to reveal steps to correct answer Solve right-angled triangle problems (1. 8) 18 Exercise A 3 Question 4 O H 4. Find the angle marked with a variable: Step 1: Label sides Step 2: A = 50 m H = 75 m Click Step 3: Previous cos(y) = 50. 0 75 = 0. 66666. . y = cos-1 (0. 666667) = 48. 2 (to 1 d. p. ) A Next Back to Start of Exercise A 3 for the next question

Solve right-angled triangle problems (1. 8) Exercise A 4 Solve mixed right-angled triangle problems Answer the six questions on page 12 of the book. Write down each question and answer and make sure you include your workings. Then click on the ‘next’ arrow to see the correct answers and the steps involved to achieving them. Previous Back to Achievement Menu Next

Click to reveal steps to correct answer Solve right-angled triangle problems (1. 8) 20 Exercise A 4 Question 1 A 1. O Find the size of the variable: H Angle involved, so trigonometry Step 1: Label sides Step 2: O = x m A = 108 m so TOA Step 3: x = 108 x tan(18) = 35. 1 (to 3 s. f. ) Previous Click Next for the next question Back to Start of Exercise A 4

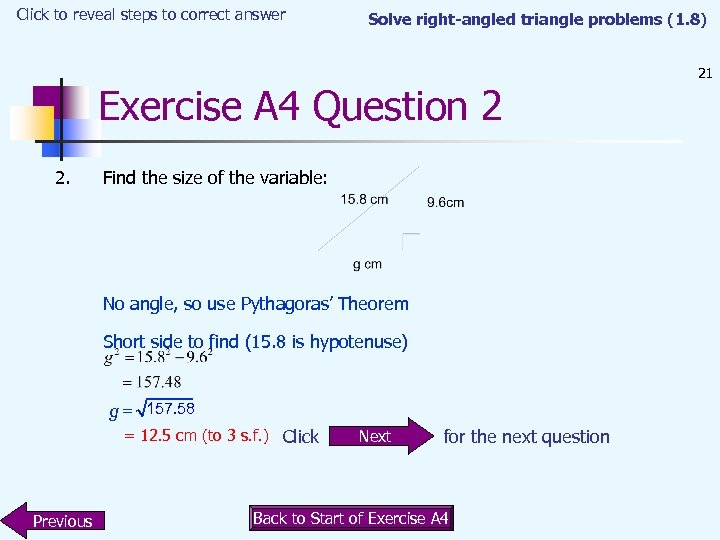Click to reveal steps to correct answer Solve right-angled triangle problems (1. 8) Exercise A 4 Question 2 2. Find the size of the variable: No angle, so use Pythagoras’ Theorem Short side to find (15. 8 is hypotenuse) g = 157. 58 = 12. 5 cm (to 3 s. f. ) Click Previous Next for the next question Back to Start of Exercise A 4 21

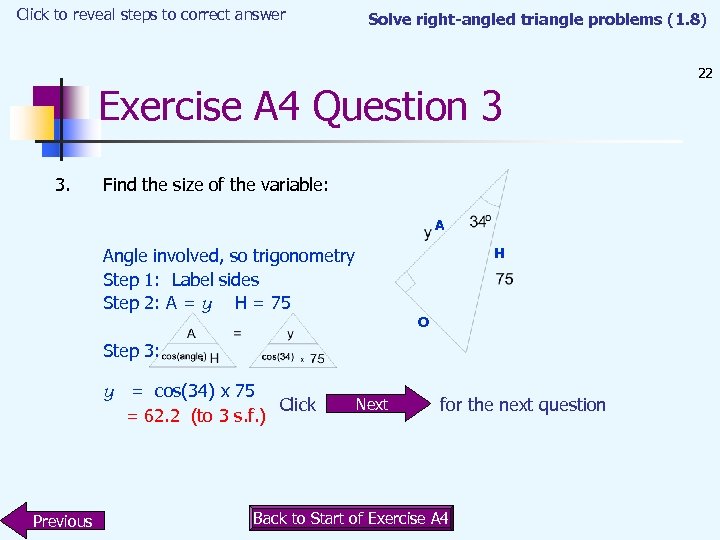Click to reveal steps to correct answer Solve right-angled triangle problems (1. 8) Exercise A 4 Question 3 3. Find the size of the variable: A H Angle involved, so trigonometry Step 1: Label sides Step 2: A = y H = 75 O Step 3: y = cos(34) x 75 Click = 62. 2 (to 3 s. f. ) Previous Next for the next question Back to Start of Exercise A 4 22

Click to reveal steps to correct answer Solve right-angled triangle problems (1. 8) 23 Exercise A 4 Question 4 4. Find the size of the variable: Angle involved, so trigonometry Step 1: Label sides Step 2: O = 59 m A = 75 m so TOA H O Step 3: tan h = 59 ÷ 75 = 0. 7866666 h = tan–¹(0. 7866666) = 38. 2 (to 3 s. f. ) Click Previous A Next Back to Start of Exercise A 4 for the next question

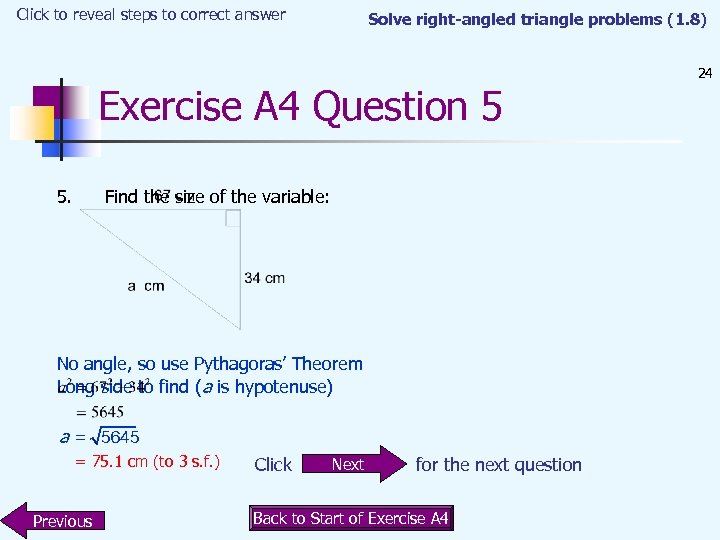Click to reveal steps to correct answer Solve right-angled triangle problems (1. 8) Exercise A 4 Question 5 5. Find the size of the variable: No angle, so use Pythagoras’ Theorem Long side to find (a is hypotenuse) a = 5645 = 75. 1 cm (to 3 s. f. ) Previous Click Next for the next question Back to Start of Exercise A 4 24

Click to reveal steps to correct answer Solve right-angled triangle problems (1. 8) 25 Exercise A 4 Question 6 6. Find the size of the variable: A H O Angle involved, so trigonometry Step 1: Label sides Step 2: O = 32. 8 m H = 45. 8 m Step 3: sin Θ = 32. 8 ÷ 45. 8 = 0. 7161572052 Θ = sin–¹(0. 7161572052) Next Click = 45. 7 (to 3 s. f. ) Previous Back to Start of Exercise A 4 for the Merit section

Solve right-angled triangle problems (1. 8) Merit Exercise Solve right-angled triangle problems in context. Answer the eleven questions on pages 18– 20 of the book. Write down each question and answer and make sure you include your workings. Then click on the ‘next’ arrow to see the correct answers and the steps involved to achieving them. Previous Back to Main Menu Next

Click to reveal steps to correct answer Solve right-angled triangle problems (1. 8) Merit Exercise Question 1 1. A building that is 5. 6 m high is to have a rope hooked from it to make an angle of 70° with the ground. How long will the rope need to be? Angle involved so Step 1: Label sides Step 2: O = 5. 6, find H so SOH Step 3: H O A Click rope = 5. 6 sin(70) = 5. 96 m or 6. 0 m (to 2 s. f. ) Previous 27 Back to Start of Merit Next for the next question

Click to reveal steps to correct answer Solve right-angled triangle problems (1. 8) 28 Merit Exercise Question 2 2. To find the height of the school flagpole, the angle from a person’s eyelevel to the top of the flagpole is measured. This angle is 23°. If the person is standing level with the base of the flagpole and 3. 5 m from it, and their eye is 1. 63 m above the ground, how tall is the flagpole? Step 1: Label sides Step 2: A = 3. 5 m O = x m so TOA Step 3: x=0 23° A = 3. 5 m 1. 63 m flag = 1. 63 + 3. 5 x tan(23) = 3. 1 m (to 3 s. f. ) Click Previous 3. 5 m Next Back to Start of Merit for the next question

Click to reveal steps to correct answer Solve right-angled triangle problems (1. 8) Merit Exercise Question 3 3. On an orienteering course, a person walks 600 m North and then on a bearing of 123° until they are exactly East of their starting point. (a) How far do they walk on this bearing? (b) How far are they from the starting point? (a) Step 1: Label sides Step 2: A = 600 m H = d m so CAH Step 3: H A O Previous d = 600 ÷ cos(57) = 1100 m (to 3 s. f. ) Click Next Back to Start of Merit for answer (b) 29

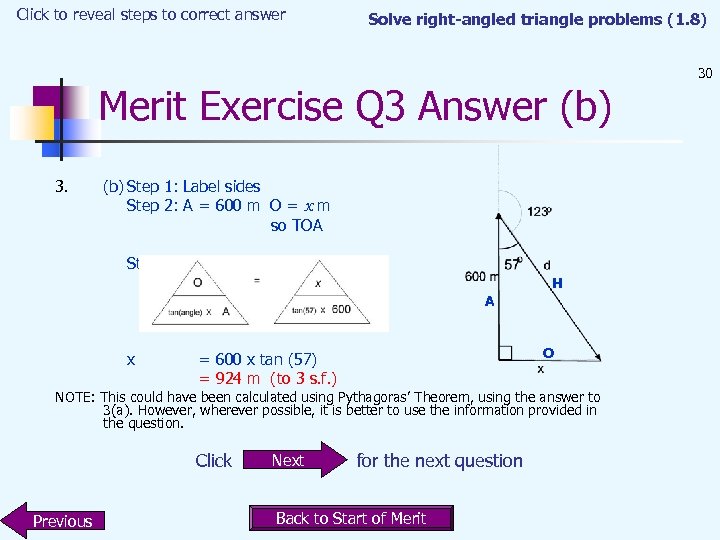Click to reveal steps to correct answer Solve right-angled triangle problems (1. 8) Merit Exercise Q 3 Answer (b) 3. (b) Step 1: Label sides Step 2: A = 600 m O = x m so TOA Step 3: H A x O = 600 x tan (57) = 924 m (to 3 s. f. ) NOTE: This could have been calculated using Pythagoras’ Theorem, using the answer to 3(a). However, wherever possible, it is better to use the information provided in the question. Click Previous Next for the next question Back to Start of Merit 30

Click to reveal steps to correct answer Solve right-angled triangle problems (1. 8) Merit Exercise Question 4 4. When crossing a river which is 4. 2 metres wide with parallel river banks, a boat forms an angle of 55° with the bank where it starts. How far down the river will the boat reach the opposite bank? Step 1: Label sides Step 2: A = d O = 4. 2 m so TOA Step 3: H O d=A d = 4. 2 ÷ tan(55) = 2. 9 m (to 2 s. f. ) Click Previous Next for the next question Back to Start of Merit 31

Click to reveal steps to correct answer Solve right-angled triangle problems (1. 8) 32 Merit Exercise Question 5 5. The forwards in a rugby team have to run along the diagonal of a rugby field and back, while the backs run round the field. The field is 100 m by 70 m. How much further do the backs run each time they have run round the field once if the forwards have run the diagonal and back? No angles, so Pythagoras’ Theorem. Long side to find. d² = 100² + 70² = 14 900 d = 14 900 = 122 m (to 3 s. f. ) Distance round field = 2(100 + 70) = 340 m Extra distance = 340 – 2(122) Start and finish point = 96 m (to 2 s. f. ) Click Previous Next d 100 m for the next question Back to Start of Merit 70 m

Click to reveal steps to correct answer Solve right-angled triangle problems (1. 8) Merit Exercise Question 6 6. A canvas length of 5 m is to be lifted and supported in the middle to form a tent. If the tent is to be 2. 1 m high, how wide will the base of the tent be, if the canvas touches the ground? No angles, so Pythagoras’ Theorem. Short side to find. d² = 2. 5² – 2. 1² = 1. 84 d = = 1. 3565 m (to 5 s. f. ) Width of tent = 2(1. 3565) = 2. 7 m (to 2 s. f. ) Click Previous Next Back to Start of Merit for the next question 33

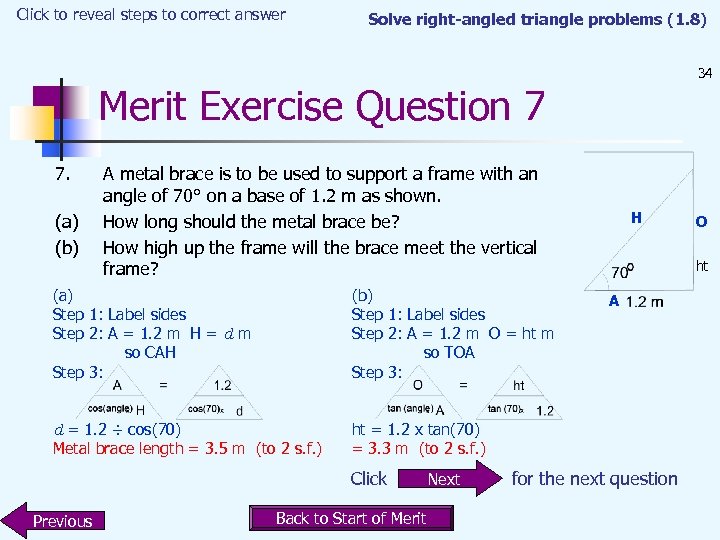Click to reveal steps to correct answer Solve right-angled triangle problems (1. 8) 34 Merit Exercise Question 7 7. (a) (b) A metal brace is to be used to support a frame with an angle of 70° on a base of 1. 2 m as shown. How long should the metal brace be? How high up the frame will the brace meet the vertical frame? (a) Step 1: Label sides Step 2: A = 1. 2 m H = d m so CAH Step 3: (b) Step 1: Label sides Step 2: A = 1. 2 m O = ht m so TOA Step 3: d = 1. 2 ÷ cos(70) Metal brace length = 3. 5 m (to 2 s. f. ) H ht ht = 1. 2 x tan(70) = 3. 3 m (to 2 s. f. ) Click Previous Back to Start of Merit Next O A for the next question

Click to reveal steps to correct answer Solve right-angled triangle problems (1. 8) 35 Merit Exercise Question 8 8. A ramp is to be used to drive a wheel of a vehicle up a height of 0. 7 m. The angle the ramp forms with the ground is 15° and the ramp is to be 0. 5 m wide. A diagonal brace is to be used as shown. How long will this brace be? (Hint: You will need to use two different right-angled triangles to solve the problem) H O A Side face can be used to find slant length Step 1: Label sides Step 2: O = 0. 7 m H = d m so SOH Step 3: O 1. 2 = sin(angle) x H sin(15) x d so: d = 0. 7 ÷ sin(15) Slant length = 2. 7 m (to 2 s. f. ) Use the right-angle triangle on slant b² = 2. 7² + 1. 2² = 8. 73 b = 8. 73 = 2. 9546 Brace length = 3. 0 m (to 2 s. f. ) Click Previous Back to Start of Merit Next for the next question

Click to reveal steps to correct answer Solve right-angled triangle problems (1. 8) 36 Merit Exercise Question 9 C Grid references using six digits have the first three digits 215620 describe the easterly co-ordinate and the second three d digits describe the northerly co-ordinate, each in metres from a point of origin. What is (a) the distance and C (b) the bearing of point C with grid reference 215620 from point D with grid reference 225580? 215620 (a) No angles, so Pythagoras’ Theorem. (b) Angles, so Long side (d) to find. Step 1: Label sides North-South distance = 620 – 580 = 40 Step 2: O = 10, A = 40 East-West distance = 225 – 215 = 10 so TOA d² = 40² + 10² = 1700 Step 3: tan x = 10 ÷ 40 = 0. 25 x = tan–¹(0. 25) = 14° (to 2 s. f. ) distance = 1700 bearing = 360 – 14 = 41 m (to 2 s. f. ) = 346 N 9. Click Previous Back to Start of Merit Next 225580 D N O 10 H A x 40 225580 D for the next question

Click to reveal steps to correct answer Solve right-angled triangle problems (1. 8) Merit Exercise Question 10 10. (a) What angle does the vector form with the horizontal axis? – 3 (b) How long is this vector? 18 Sketch vector gives: (a) Angle, so Step 1: Label sides Step 2: O = 18, A = 3 so TOA O d Step 3: tan x = 18 ÷ 3 = 6 A x = tan–¹(6) = 80. 5° (to 1 d. p. ) (b) No angles, so Pythagoras’ Theorem. Long side to find. d² = 18² + 3² = 333 distance = = 18. 2 m (to 3 s. f. ) Note: Angle could also be written as 180 – 80. 5 = 99. 5° Click Previous 37 Back to Start of Merit Next for the next question

Click to reveal steps to correct answer Solve right-angled triangle problems (1. 8) 38 Merit Exercise Question 11 11. A chair has a square seat with 4 legs 65 cm long and 80 cm apart. A bar joining two of the adjacent legs is bolted 2 cm from the floor. If the bar is to form an angle of 36 o with a line parallel to the floor, find: (a) how far up the leg the bolt hole should be drilled (b) the length of the bar between bolt holes. (a) Angle involved, so Step 1: Label sides H O Step 2: O = d, A = 80 cm so TOA A Step 3: tan 36 = d ÷ 80 d = 80 x tan (36) = 58. 1 (to 3 s. f. ) Distance up leg = 58. 1 + 2 = 60. 1 cm Click Previous Next (b) Angle involved, so Step 1: Label sides Step 2: H = b, A = 80 cm so CAH Step 3: b = 80 ÷ cos (36) Length of bar = 98. 9 cm (to 3 s. f. ) for the Excellence section Back to Start of Merit H O A

Solve right-angled triangle problems (1. 8) Excellence Exercise Solve right-angled triangle problems in three-dimensional situations. Answer the eleven questions on pages 24– 26 of the book. Write down each question and answer and make sure you include your workings. Then click on the ‘next’ arrow to see the correct answers and the steps involved to achieving them. Previous Back to Main Menu Next

Click to reveal steps to correct answer Solve right-angled triangle problems (1. 8) Excellence Exercise Question 1 1. 40 A chair has a square seat with 4 legs 65 cm long and 80 cm apart. A bar parallel to the floor joining two diagonally opposite legs is bolted 2 cm from the floor. Another bar is slanted to join diagonally opposite legs 2 cm from the floor and 2 cm from the seat on the other leg. (a) What is the length of each of the bars between bolt holes? (b) What angle is there between the horizontal bar and the slanted bar? (a) Shorter bar’s length = d. d² = 80² + 80² = 12 800 d = 12 800 = 113 cm (3 s. f. ) Longer bar’s length = b. With 2 cm above and below, leg part of triangle is 61 cm. b² = d² + 61² = 12 800 + 3271 = 16 521 d = 16 521 = 129 cm (3 s. f. ) Click Previous Back to Start of Excellence Next for answer 1 (b)

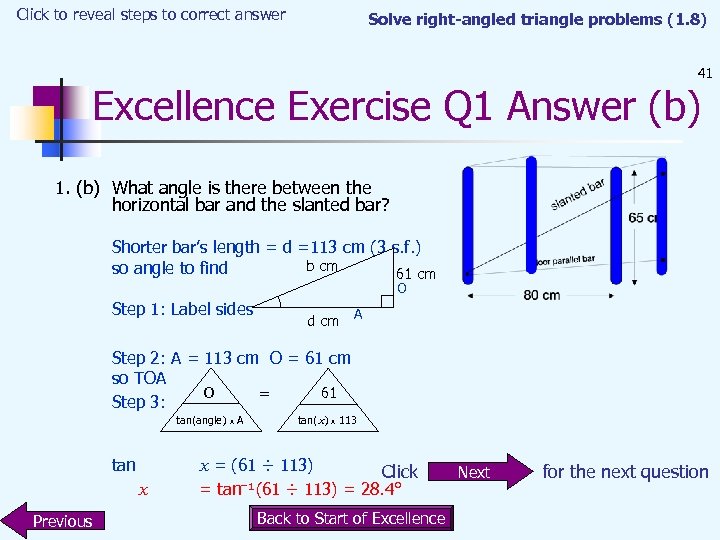Click to reveal steps to correct answer Solve right-angled triangle problems (1. 8) 41 Excellence Exercise Q 1 Answer (b) 1. (b) What angle is there between the horizontal bar and the slanted bar? Shorter bar’s length = d =113 cm (3 s. f. ) b cm so angle to find 61 cm O Step 1: Label sides d cm A Step 2: A = 113 cm O = 61 cm so TOA O 61 = Step 3: tan(angle) x A tan x Previous tan(x) x 113 x = (61 ÷ 113) Click – = tan ¹(61 ÷ 113) = 28. 4° Back to Start of Excellence Next for the next question

Click to reveal steps to correct answer Solve right-angled triangle problems (1. 8) Excellence Exercise Question 2 2. Previous A ladder is 2. 8 m long and is leaning against the wall of a house from a point 1. 2 m out from the base of the wall. The ladder can be extended to become 3. 6 m long. How much further up the wall does the ladder reach when it is extended? Normal height = d, extended = e. No angles, so Pythagoras’ Theorem, Short side to find. e² = 3. 6² – 1. 2² = 11. 52 e= = 3. 39 m (to 3 s. f. ) d² = 2. 8² – 1. 2² = 6. 4 d= = 2. 53 m (to 3 s. f. ) Distance up wall = (3. 39 – 2. 53) m = 0. 86 m Next Click for the next question Back to Start of Excellence 42

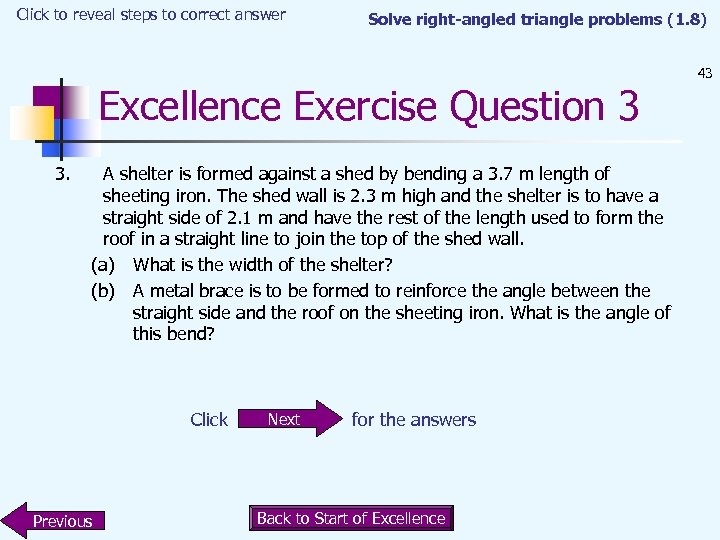Click to reveal steps to correct answer Solve right-angled triangle problems (1. 8) Excellence Exercise Question 3 3. A shelter is formed against a shed by bending a 3. 7 m length of sheeting iron. The shed wall is 2. 3 m high and the shelter is to have a straight side of 2. 1 m and have the rest of the length used to form the roof in a straight line to join the top of the shed wall. (a) What is the width of the shelter? (b) A metal brace is to be formed to reinforce the angle between the straight side and the roof on the sheeting iron. What is the angle of this bend? Click Previous Next for the answers Back to Start of Excellence 43

Click to reveal steps to correct answer Solve right-angled triangle problems (1. 8) Excellence Exercise Q 3 Answer O H 3 (a) What is the width of the shelter? Long side = 1. 6 m Short side = 2. 3 – 2. 1 = 0. 2 m d² = 1. 6² – 0. 2² = 2. 52 d= = 1. 6 m (2 s. f. ) 3 (b) A metal brace is to be formed to reinforce the angle between the straight side and the roof on the sheeting iron. What is the angle of this bend? Angle to find. Label sides O = 0. 2 m, H = 1. 6 m so SOH sin x = (0. 2 ÷ 1. 6) x = sin–¹(0. 125) = 7. 2° Next Click for the next question Therefore angle of brace = 97. 1° Previous Back to Start of Excellence 44

Click to reveal steps to correct answer Solve right-angled triangle problems (1. 8) 45 Excellence Exercise Question 4 4. A swimming pool is to be dug out of the ground. The side view crosssection is a trapezium shape, with a length of 25 m. The pool is to be 1. 2 m deep at one end and 2. 8 m deep at the other end. If digging starts at the shallow (1. 2 m) end, what angle should be used to ensure that the pool will be 2. 8 m deep when the 25 m length is dug? Step 1: Label sides Step 2: A = 25 O = (2. 8 – 1. 2) m = 1. 6 m so TOA Step 3: tan(x) = 1. 6 ÷ 25 = 0. 064 Click x = tan– 1(0. 064) = 3. 7° (to 2 s. f. ) Next A O for the next question Note: Make sure you used tan, not sin as they both give the same angle. Previous Back to Start of Excellence

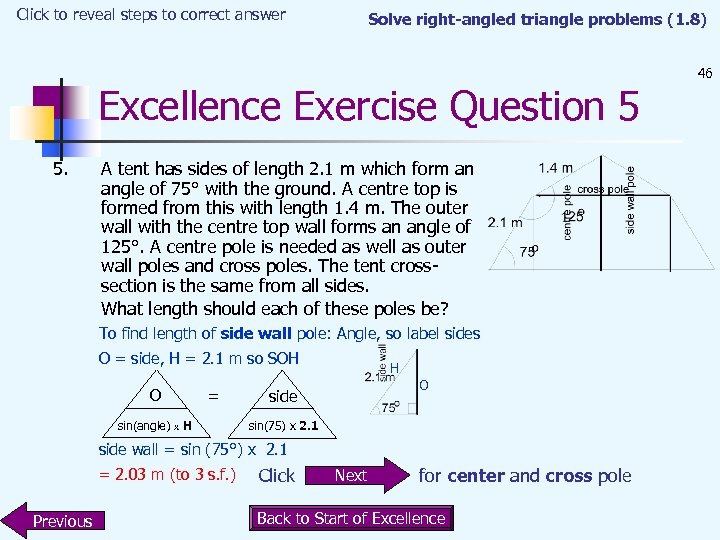Click to reveal steps to correct answer Solve right-angled triangle problems (1. 8) Excellence Exercise Question 5 5. A tent has sides of length 2. 1 m which form an angle of 75° with the ground. A centre top is formed from this with length 1. 4 m. The outer wall with the centre top wall forms an angle of 125°. A centre pole is needed as well as outer wall poles and cross poles. The tent crosssection is the same from all sides. What length should each of these poles be? To find length of side wall pole: Angle, so label sides O = side, H = 2. 1 m so SOH O = sin(angle) x H H O side sin(75) x 2. 1 side wall = sin (75°) x 2. 1 = 2. 03 m (to 3 s. f. ) Previous Click Next for center and cross pole Back to Start of Excellence 46

Click to reveal steps to correct answer Solve right-angled triangle problems (1. 8) 47 Excellence Exercise Q 5 Answer (b) H Centre pole = side wall pole + f x = 125° – (90° – 75°) – 90° = 20° Angle, so label sides: O = f, H = 1. 4 m so SOH f = sin(20°) x 1. 4 = 0. 48 m Centre pole = 2. 03 m + 0. 48 m = 2. 51 m Find cross-pole by calculating half length = d Angle, so label sides: A = d, H = 1. 4 m d = cos(20°) x 1. 4 = 1. 32 m Cross-pole = 1. 32 m + 1. 32 m Next for the next question = 2. 64 m Click Previous Back to Start of Excellence A f. O

Click to reveal steps to correct answer Solve right-angled triangle problems (1. 8) Excellence Exercise Question 6 6. When throwing the discus, Anna’s throw is in line with the centre of the throwing circle and a distance of 25. 6 m straight out in the middle of the allowable sector. Bernice’s throw is on an angle of 12 o from the middle and is a perpendicular distance of 24. 8 m. Who threw the greatest throw and by how much? Angles, so label sides: A = 24. 8, H = d so CAH A 24. 8 m = cos(angle) x H cos(12) x d A 12° d = 24. 8 ÷ cos(12) = 25. 35 m Anna wins by (25. 6 – 25. 35) = 0. 25 m Click Previous 48 Back to Start of Excellence H d Next for the next question

Click to reveal steps to correct answer Solve right-angled triangle problems (1. 8) Excellence Exercise Question 7 7. A ramp has the dimensions shown. That is, at ground level the base is a rectangle 2. 5 m by 0. 5 m. The ramp starts from ground level and reaches a vertical height of 0. 7 m. A metal brace fits diagonally over the ramp. What angle does the diagonal metal brace make with the ground? Distance along diagonal of base = d d² = 2. 5² + 0. 5² = 6. 5 d = = 2. 55 m (3 s. f. ) 2. 5 m Use triangle formed by brace and diagonal on base. Step 1: Label sides A Step 2: A = d = 2. 55 m, O = 0. 7 m, so TOA Step 3: tan (x) = 0. 7 ÷ 2. 55 Angle = 15. 5° (to 1 d. p. ) Previous Click Next Back to Start of Excellence O for the next question 49

Click to reveal steps to correct answer Solve right-angled triangle problems (1. 8) Excellence Exercise Question 8 8. There are council rules to decide how close you can build and how high at the boundary. They have a ‘building envelope’ within which people must build, unless they get approval and their neighbour’s permission. One such rule is that no-one may build within 2 m of the boundary. At the 2 m edge, the building may be 2. 5 m tall, and be within a slant of 25°. If a building is to be 3 m high, under this rule, what is the closest it can be to the boundary to fit in the building envelope? 25° boundary edge 2. 5 m Click Next 2 m Previous Back to Start of Excellence for the answer 50

Click to reveal steps to correct answer Solve right-angled triangle problems (1. 8) Excellence Exercise Q 8 Answer 9. If a building is to be 3 m high, what is the closest it can be to the boundary to fit in the building envelope? O Height on slant = 3. 0 m – 2. 5 m = 0. 5 m H boundary edge Angle involved, so label sides O = 0. 5 m, H = d, so SOH d = 0. 5 ÷ tan(25) = 1. 07 (to 3 s. f. ) Click Therefore distance = 2 + 1. 07 = 3. 07 m Previous Back to Start of Excellence 51 25° 2. 5 m 2 m Next for the next question

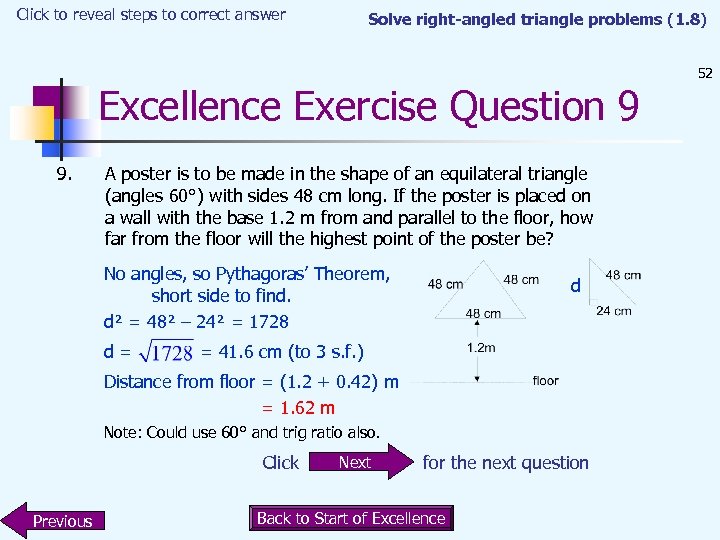Click to reveal steps to correct answer Solve right-angled triangle problems (1. 8) Excellence Exercise Question 9 9. A poster is to be made in the shape of an equilateral triangle (angles 60°) with sides 48 cm long. If the poster is placed on a wall with the base 1. 2 m from and parallel to the floor, how far from the floor will the highest point of the poster be? No angles, so Pythagoras’ Theorem, short side to find. d² = 48² – 24² = 1728 d= d = 41. 6 cm (to 3 s. f. ) Distance from floor = (1. 2 + 0. 42) m = 1. 62 m Note: Could use 60° and trig ratio also. Click Previous Next for the next question Back to Start of Excellence 52

Click to reveal steps to correct answer Solve right-angled triangle problems (1. 8) 53 Excellence Exercise Question 10 10. A garden is an isosceles trapezium shape with parallel sides 3. 2 m and 5. 6 m long. The width of the garden is 2. 5 m. A path is being formed around the whole garden and boxing (lengths of timber) needs to be placed around the garden edge and the outside of the path. The path is 0. 9 m wide along the garden edge and forms a part circle at each corner. What length of boxing is needed? Let slanted length = d. Triangle at each end has height 2. 5 m Base = half of (5. 6 m – 3. 2 m) = 1. 2 m d² = 2. 5² + 1. 2² = 7. 69 d= = 2. 8 m (2 s. f. ) 3. 2 m d d 2. 5 m d 5. 6 m 1. 2 m Therefore inner edge length = (3. 2 + 5. 6 + 2(2. 8)) = 14. 4 m Outer edge = 14. 4 m + (1. 8) m = 20. 1 m (1 d. p. ) Total needed = 14. 4 + 20. 1 m = 34. 5 m Click Previous Back to Start of Excellence Next for the next question

Click to reveal steps to correct answer Solve right-angled triangle problems (1. 8) Excellence Exercise Question 11 11. 54 An estimate for the height of a hill can be made by walking along ground level towards the hill. If the hilltop forms an angle of 17° and after walking 60 m closer forms an angle of 25°, estimate the height of the hill. In first triangle, this means tan 17 = h 60 + h tan 25 Multiplying through gives: 60 tan 17 + h tan 25 tan 17 = h Putting h terms on one side: 60 tan 17 = h – h tan 25 tan 17 60 tan 17 = h(1 – tan 25 tan 17) 60 tan 17 Rearrange: =h 1 – tan 25 tan 17 so h = 21 m (2 s. f. ) Click Previous Next for Achievement Standard 90153 Back to Start of Excellence

Use geometric reasoning to solve problems (1. 9) Achievement Standard 90153 Use geometric reasoning to solve problems (1. 9) Previous Back to Main Menu Next

Use geometric reasoning to solve problems (1. 9) Achievement Exercise Using angle rules to solve problems Answer the ten questions on pages 36– 38 of the book. Write down each question and answer and make sure you include your workings. Then click on the ‘next’ arrow to see the correct answers and the steps involved to achieving them. Previous Back to Main Menu Next

Click to reveal steps to correct answer Use geometric reasoning to solve problems (1. 9) Achievement Exercise Question 1 1. ABC is an isosceles triangle. ACD is a right-angled triangle. Find p. CBA ACD p p = = 58° (base of isos triangle) 180 – 2(58) = 64° ( sum triangle) 90° – 64° (to form right ) 26° Click Previous Next for the next question Back to Start of Achievement 57

Click to reveal steps to correct answer Use geometric reasoning to solve problems (1. 9) Achievement Exercise Question 2 2. DEHI is a kite. EFGH is a rhombus with sides equal in length to the long side of the kite. Find b. IHE = 130° (1 pr. opp. of kite equal) GHE = 360° – 130° – 162° = 68° ( at point ) b = 68° (opp. of rhombus are equal) Click Previous Next for the next question Back to Start of Achievement 58

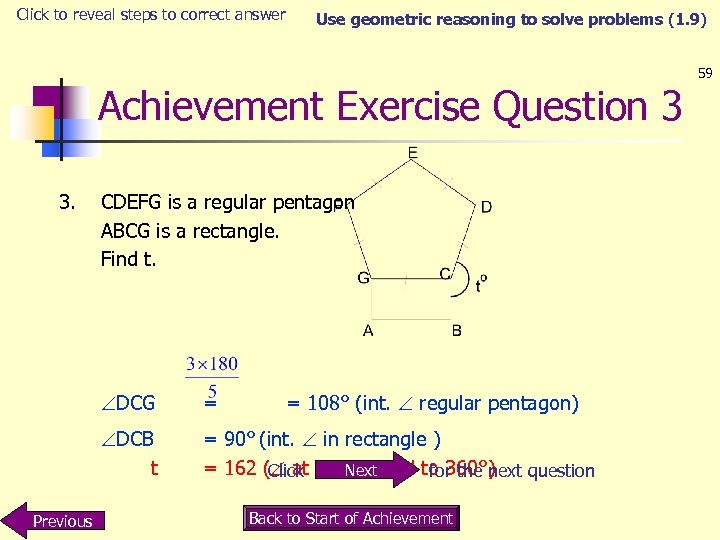Click to reveal steps to correct answer Use geometric reasoning to solve problems (1. 9) Achievement Exercise Question 3 3. CDEFG is a regular pentagon ABCG is a rectangle. Find t. DCG DCB t Previous = = 108° (int. regular pentagon) = 90° (int. in rectangle ) = 162 ( at a point add to 360°) Next Click for the next question Back to Start of Achievement 59

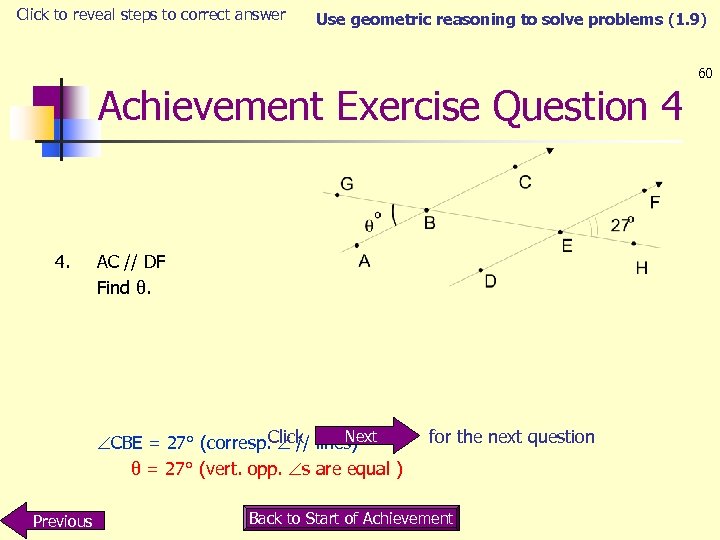Click to reveal steps to correct answer Use geometric reasoning to solve problems (1. 9) Achievement Exercise Question 4 4. AC // DF Find θ. Next CBE = 27° (corresp. Click lines) // θ = 27° (vert. opp. s are equal ) Previous for the next question Back to Start of Achievement 60

Click to reveal steps to correct answer Use geometric reasoning to solve problems (1. 9) Achievement Exercise Question 5 5. PQ // RS PQ = PR Find m PQR PRQ m Previous = 56° (alternate // lines) Click = 56° (base isos. Next triangle) for the next question = 68° (Sum s triangle PQR is 180°) Back to Start of Achievement 61

Click to reveal steps to correct answer Use geometric reasoning to solve problems (1. 9) Achievement Exercise Question 6 6. AB = 7 cm. BC = 3 cm. CD = 9. 8 cm Find length of BE, x cm. ABE = ACD (corresponding // lines) AEB = ADC (corresponding // lines) Therefore triangles ABE and ADC are similar. Scale factor = 10 ÷ 7 (length AC divided by length AB) BE = 9. 8 ÷ (10 ÷ 7) Next Click for the next question = 6. 86 cm Previous Back to Start of Achievement 62

Click to reveal steps to correct answer Use geometric reasoning to solve problems (1. 9) Achievement Exercise Question 7 7. ABCDE is a pentagon. Find x. Internal s of pentagon add to 3 x 180° = 540° 120 + 98 + 90 = 398 CDE = (540 – 398)° = 142° x = 180 – 142 = 38° (Adjacent straight line) Next Click Previous 63 Back to Start of Achievement for the next question

Click to reveal steps to correct answer Use geometric reasoning to solve problems (1. 9) Achievement Exercise Question 8 8. BD = DC Find f. D E 113 o fo 75 o CBD = 75° (base isos. triangle. C BDC) A B BDC = 30° ( sum triangle BDC) Internal s of quadrilateral is 2 x 180° = 360° f + 30 + 75 + 90 + 113 = 360 f = 360 – 308 = 52° Next Click for the next question Previous Back to Start of Achievement 64

Click to reveal steps to correct answer Use geometric reasoning to solve problems (1. 9) Achievement Exercise Question 9 9. Dukes Street, Princess Street and Queen Street are parallel streets. High Street and Low Street meet at right angles. What angle does Low Street form with Queen Street (angle b)? High Street meets Princess Street at angle 35° (alternate angles between parallel lines) Low Street meets Princess Street at angle 55° (as Low Street High Street) b = 55° (alternate angles between parallel lines) Click Previous Next for the next question Back to Start of Achievement 65

Click to reveal steps to correct answer Use geometric reasoning to solve problems (1. 9) 66 Achievement Exercise Question 10 10. PQRST is a regular polygon TS // UW Find c. STU = = 72° (exterior angle of regular pentagon) c = (180 – 72)° =Click (co-interior angles // lines) 108° Next for the Merit section c = 108 Previous Back to Start of Achievement

Use geometric reasoning to solve problems (1. 9) Merit Exercise Using circle angle rules to solve problems Answer the nine questions on pages 46– 48 of the book. Write down each question and answer and make sure you include your workings. Then click on the ‘next’ arrow to see the correct answers and the steps involved to achieving them. Previous Back to Main Menu Next

Click to reveal steps to correct answer Use geometric reasoning to solve problems (1. 9) Merit Exercise Question 1 1. ABC is an isosceles triangle BCD is a right-angled triangle AC // BD Find p. CAB = p° (base of isos triangle) ACB = (180° – 2 p)° ( sum of triangle ABC) CBD = (180° – 2 p)° (alt // lines ) (180 – 2 p) + 90 + 28 = 180 ( sum of triangle BCD) 2 p = 118 p = 59 Next Click for the next question Previous Back to the Start of Merit 68

Click to reveal steps to correct answer Use geometric reasoning to solve problems (1. 9) Merit Exercise Question 2 2. V, W and X lie on circle centre O XT is tangent to the circle. If VWX = 56°, find q. VOX = 112° ( at centre = 2 x at circumference) VXO = ½(180° – 112)° (base isos triangle from radii) = 34° OXT = 90° (radius tangent ) q = 90 – 34 Next Click for the next question q = 56 Previous Back to the Start of Merit 69

Click to reveal steps to correct answer Use geometric reasoning to solve problems (1. 9) Merit Exercise Question 3 3. A trophy design has a regular pentagon as a centre piece. It is surrounded by equilateral triangles on each edge. The frame holding it is made from the line segments IK, KL and LG, where IG is parallel to KL. The frame bisects the angle between the triangles as shown in the diagram. Angle a, is between the line segments GL and LK on the frame. What size is this angle? EGI = 108° (Int. in regular pentagon ) EGF = IGH = 60° (Interior equilateral) 2 EGF + 108° + 2 x 60° = 360° ( at point ) EGF = 66° IGL = 126° a = 180 – 126 = 54 (Co-interior // lines add to 180°) Next Click for the next question Previous Back to the Start of Merit 70

Click to reveal steps to correct answer Use geometric reasoning to solve problems (1. 9) 71 Merit Exercise Question 4 4. Player 1, player 2 and player 3 are running parallel. The ball is being passed between them. Player 2 passes on an angle of 75° to player 1 who immediately returns it to player 2 who receives the ball on an angle of 82°. The ball is immediately passed to player 3’s line on an angle of 75°. The distance this ball travels is the same distance that B player 2 has run while the ball had been passed to and received from player 1. If player 2 had passed the ball directly to this end point from the start, what angle would player 2 need to have passed on (marked as size v°)? D C A Label diagram with points to be able to clearly identify angles by name. ACD = 105° (Adj on straight line add to 180°) 2 v = 180 – 105 (Base isos triangle and sum triangle) 2 v = 75 Next v = 37. 5 Click for Previous Back to the Start of Merit the next question

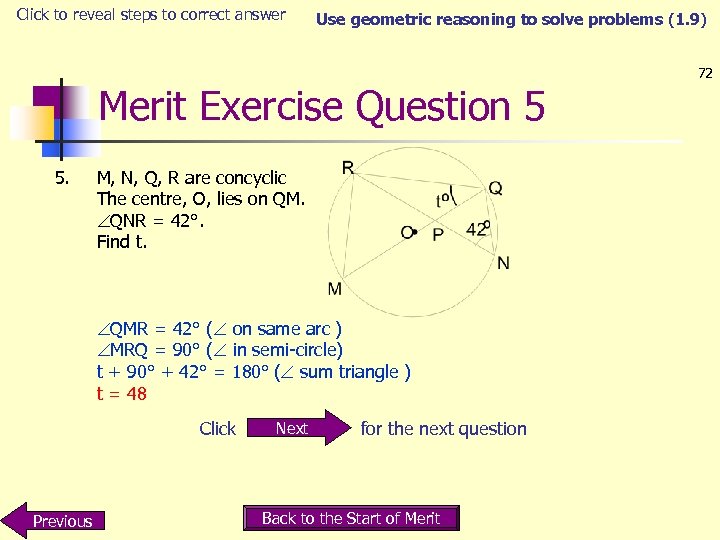Click to reveal steps to correct answer Use geometric reasoning to solve problems (1. 9) Merit Exercise Question 5 5. M, N, Q, R are concyclic The centre, O, lies on QM. QNR = 42°. Find t. QMR = 42° ( on same arc ) MRQ = 90° ( in semi-circle) t + 90° + 42° = 180° ( sum triangle ) t = 48 Click Previous Next for the next question Back to the Start of Merit 72

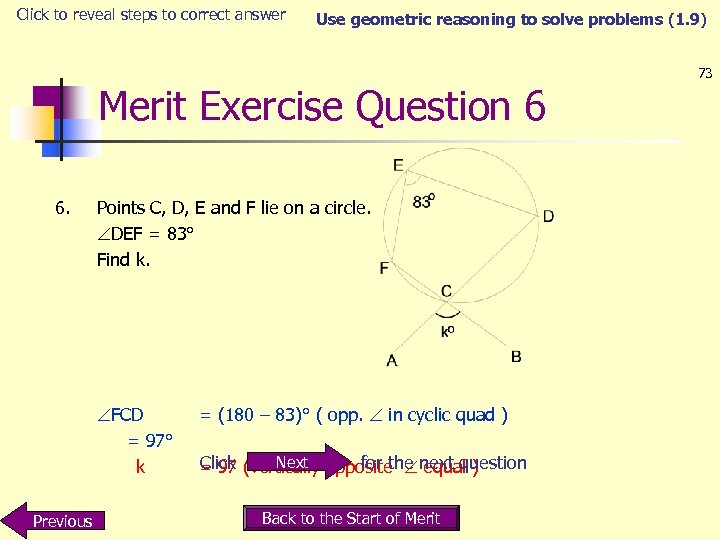Click to reveal steps to correct answer Use geometric reasoning to solve problems (1. 9) Merit Exercise Question 6 6. Points C, D, E and F lie on a circle. DEF = 83° Find k. FCD = 97° k Previous = (180 – 83)° ( opp. in cyclic quad ) Next Click for the equal ) = 97 (vertically opposite next question Back to the Start of Merit 73

Click to reveal steps to correct answer Use geometric reasoning to solve problems (1. 9) Merit Exercise Question 7 7. A ball is to be sent along the dashed lines to point Z from point A. It bounces off the linear barrier XY. Each time it hits a barrier, the ball bounces off at an angle that is the same as the angle it hit the barrier. The side walls are parallel and the barrier XY is at an angle of 150° as shown. Find f, the angle that the ball needs to hit the left side wall, to hit point Z. Click Previous Next for the answer Back to the Start of Merit 74

Click to reveal steps to correct answer Use geometric reasoning to solve problems (1. 9) Merit Exercise Q 7 Answer Extend XY to right wall at point W and label point V. WMP = 40° (from info given) XWP = 30° (co-interior between parallel lines add to 180°) WPM = 180° – (40 + 30)° (sum triangle WPM ) = 110° VPM = 180° – 110° = 70° (adj straight line ) WPZ = 70° (from info given) f = 70 (alternate between parallel lines are equal) Next Click for the next question Previous Back to the Start of Merit 75

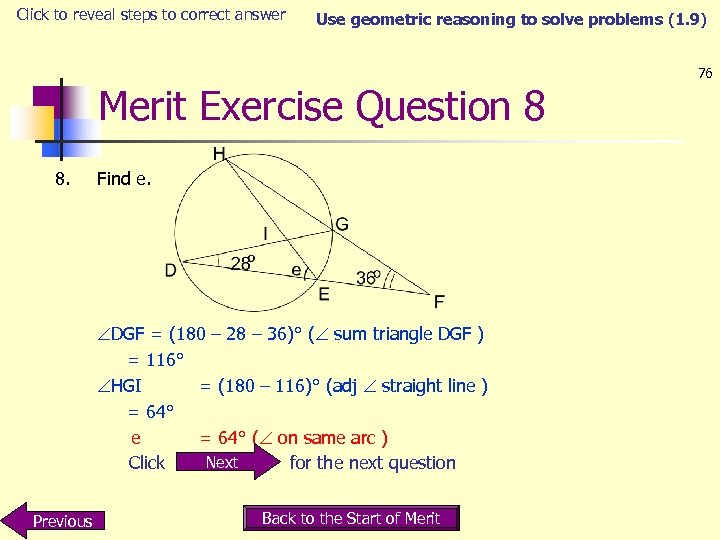Click to reveal steps to correct answer Use geometric reasoning to solve problems (1. 9) Merit Exercise Question 8 8. Find e. DGF = (180 – 28 – 36)° ( sum triangle DGF ) = 116° HGI = (180 – 116)° (adj straight line ) = 64° e = 64° ( on same arc ) Next Click for the next question Previous Back to the Start of Merit 76

Click to reveal steps to correct answer Use geometric reasoning to solve problems (1. 9) Merit Exercise Question 9 9. A yacht is tacking as shown by solid lines in the diagram. Find y so that the yacht tacks back over the East-West line (EW) from the start at an angle of 30° as shown in the diagram. If all lines considered to be solid, this forms a pentagon. After first tack internal angle = 98° (adj straight line add to 180°) After second tack, internal angle = 180 + 37 = 217° The 4 angles of the pentagon added is 42 + 98 + 217 + 30 = 387° Interior angles of pentagon add to 3 x 180° = 540° Remaining internal angle = (540 – 387)° = 153° y = 27 (adj straight line add to 180°) Click Previous Next Back to the Start of Merit for the Excellence section 77

Use geometric reasoning to solve problems (1. 9) Excellence Exercise Using geometric proofs to solve problems Answer the eight questions on pages 52– 53 of the book. Write down each question and answer and make sure you include your workings. Then click on the ‘next’ arrow to see the correct answers and the steps involved to achieving them. Previous Back to Main Menu Next

Click to reveal steps to correct answer Use geometric reasoning to solve problems (1. 9) Excellence Exercise Question 1 1. ST // VU Prove that S, T, U and V lie on a circle. X Name intersecting value as X SUV = a° (alt // lines) VXU = (180 – 2 a)° (adj straight line) UVX = (180 – a – (180 – 2 a))° ( sum triangle) = a° UST and UVT both have same chord (arc) base of UT. Angles on same arc (or chord) are equal, so V, U, S and T are cyclic. Next Click for the next question Previous Back to Start of Excellence 79

Click to reveal steps to correct answer Use geometric reasoning to solve problems (1. 9) Excellence Exercise Question 2 2. PR // TV Find x showing all working and reasoning thoroughly. X x Insert parallel line through S QSX = 51° (alt // line ) XSU = 34° (alt // line ) W USQ = QSX + XSU = 85° Next Click for the next question Previous Back to Start of Excellence 80

Click to reveal steps to correct answer Use geometric reasoning to solve problems (1. 9) Excellence Exercise Question 3 3. Prove that the angle between a tangent and a chord is equal to the angle on the chord (that is, CAB = BCD ) x Let BAC = x BOC = 2 x ( at centre – 2 x at circumference ) BCO + CBO = 180° – 2 x ( sum triangle) BCO = 0. 5 (180° – 2 x) ( Base isos triangle equal ) = 90° – x OCD = 90° (radius tangent) BCD = 90° – (90° – x) = x Next Therefore BAC = BCD Click for the next question Previous Back to Start of Excellence 81

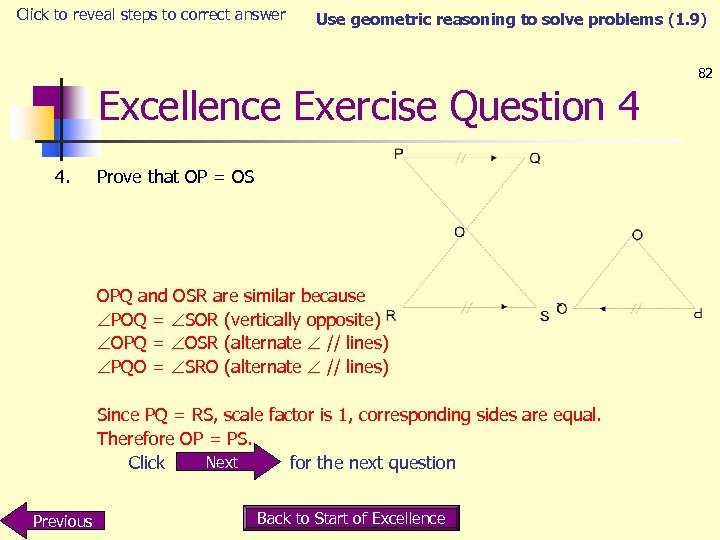Click to reveal steps to correct answer Use geometric reasoning to solve problems (1. 9) Excellence Exercise Question 4 4. Prove that OP = OS OPQ and OSR are similar because POQ = SOR (vertically opposite) OPQ = OSR (alternate // lines) PQO = SRO (alternate // lines) Since PQ = RS, scale factor is 1, corresponding sides are equal. Therefore OP = PS. Next Click for the next question Previous Back to Start of Excellence 82

Click to reveal steps to correct answer Use geometric reasoning to solve problems (1. 9) Excellence Exercise Question 5 5. A dodecagon is formed by tessellating 3 small regular hexagons as shown. In each hexagon the outside edges are extended. These extended sides meet at points P, Q and R. Using this information, prove that the large hexagon with P, Q and R as three of its vertices is also regular. Interior regular hexagon = (4 x 180° ÷ 6) = 120° Exterior regular hexagon = 60° The angle where the two hexagons meet must be (360° – 120°) = 120° ( s at a point) The remaining angle in the quadrilateral (at P, Q and R) = (360° – 120° – 60°) = 120° ( sum in quadrilateral) Therefore all internal angles in outside hexagon are 120° which means the hexagon is regular. Click Previous Next for the next question Back to Start of Excellence 83

Click to reveal steps to correct answer Use geometric reasoning to solve problems (1. 9) Excellence Exercise Question 6 6. Investigate the conjecture that ‘no parallelogram is concyclic’. Opposite angles of parallelograms are equal. Opposite angles of cyclic quadrilaterals add to 180°. Therefore if a parallelogram is concyclic, the opposite angles are equal and add to 180°. This means that the opposite angles have to be 90° which means the parallelogram is a rectangle. Therefore conjecture is not true as a special parallelogram called a rectangle is concyclic. Click Previous Next for the next question Back to Start of Excellence 84

Click to reveal steps to correct answer Use geometric reasoning to solve problems (1. 9) Excellence Exercise Question 7 7. KLMN is a kite formed in a circle, with LN as the diameter of the circle. An isosceles triangle is formed with MN, the long side of the kite, as the base and P on the circumference as the vertex of the triangle. The equal sides of the isosceles triangle are the same length as the radius of the circle. Find the size of angle KMN. Form triangle NOP. Since NP = radius, this is an equilateral triangle so angles are 60°. With same reasoning, POM is equilateral triangle. MOL = 180° – (60° + 60°) (adj straight line) Therefore MOL is also an equilateral triangle, and NLM = 60°. LMN = 90° ( in a semi-circle) LNM = 180° – 90° – 60° ( sum in triangle LMN) = 30° Because of line of symmetry, LNM = LNK Since these two angles form KNM, KNM = 30° + 30° = 60° Next Click for the next question Previous Back to Start of Excellence 85

Click to reveal steps to correct answer Use geometric reasoning to solve problems (1. 9) 86 Excellence Exercise Question 8 8. P is a point outside the circle. A, B, C and D are cyclic as shown. Show that PB x PA = PC x PD. ABD = ACD ( on same arc) Since adjacent angles on a straight line add to 180°, PBD = PCA BPD = APC (same angle) Therefore the triangles PBD and PDC are similar. Using scale factor, k, PC = k x PB and PA = k x PD Rearranging Multiplying through this gives PD x PC = PA x PB, which can be rearranged with sides swapped to give the required equation: PB x PA = PC x PD Previous Back to Main Menu End Slide Show