Паспортная прямая при решении задач на нахождение

«Паспортная» прямая при решении задач на нахождение отношений между отрезками Я – «паспортная прямая»

Основа метода: • обобщённая теорема Фалеса; • при проецировании на «паспортную» прямую нельзя проводить прямые, параллельные тем, на которых есть рассматриваемые отношения

Менелай Александрийский • I век, древнегреческий математик и астроном. Автор работ по сферической тригонометрии. Для получения формул сферической тригонометрии использовал теорему о прямой, пересекающей стороны треугольника (т. Менелая).

Теорема Менелая • Если прямая пересекает стороны АВ, ВС, АС треугольника АВС (или их продолжения) в точках К, L, М соответственно, то справедливо соотношение

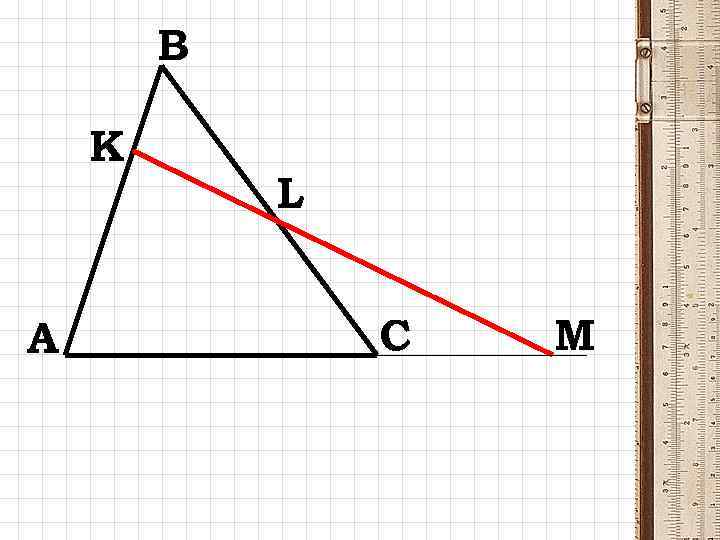В К А L С М

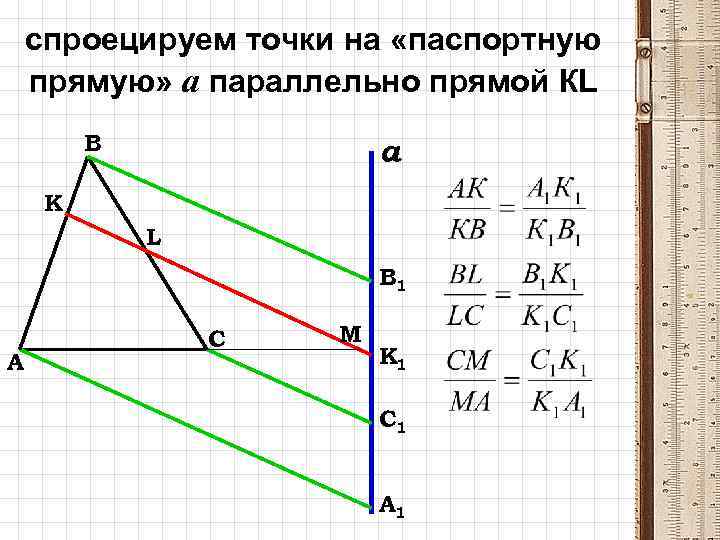спроецируем точки на «паспортную прямую» а параллельно прямой КL В а К L В 1 А С М К 1 С 1 А 1

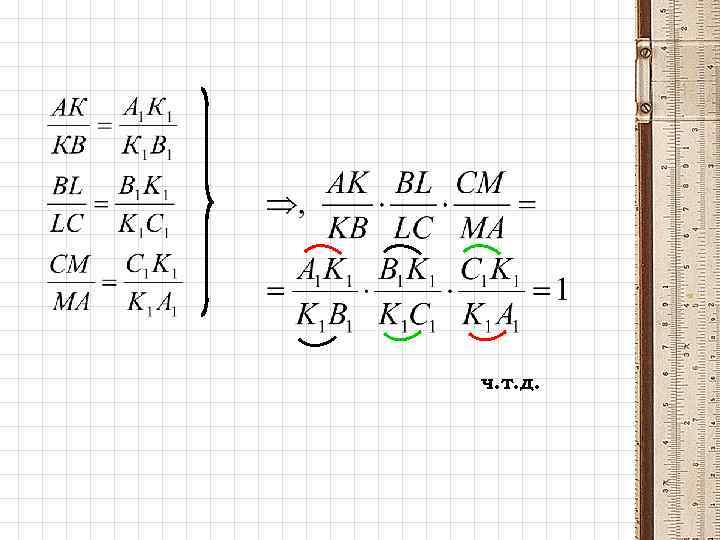ч. т. д.

Теорема Чевы • Чева Джованни (03. 1648, Милан – 13. 12. 1734, Мантуя) – итальянский инженер и математик. Окончил Пизанский университет. Основные работы по геометрии и механике. Доказал (1678 г) теорему, которая сейчас носит его имя, построил учение о секущих.

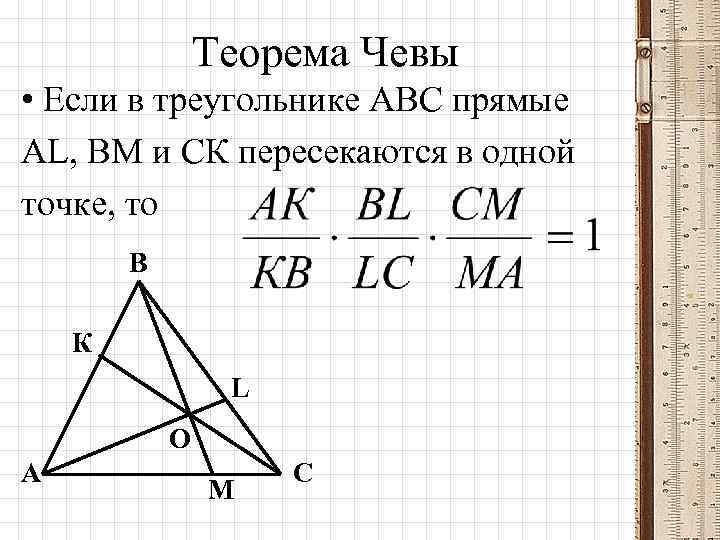Теорема Чевы • Если в треугольнике АВС прямые АL, ВМ и СК пересекаются в одной точке, то В К L О А М С

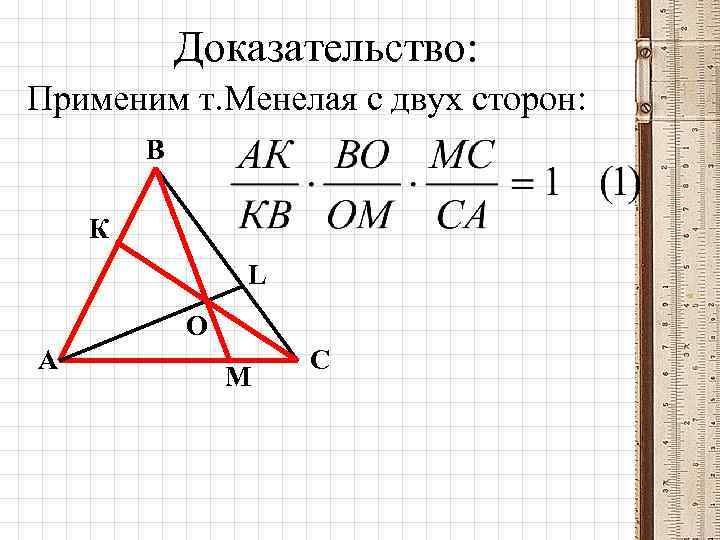Доказательство: Применим т. Менелая с двух сторон: В К L О А М С

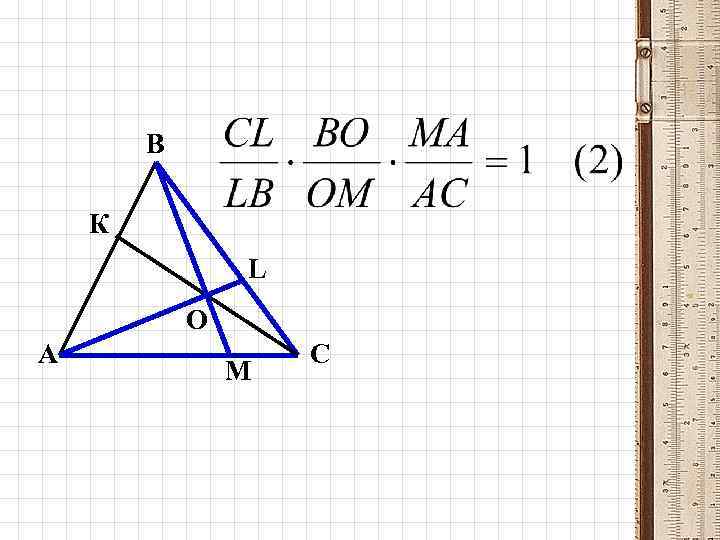В К L О А М С

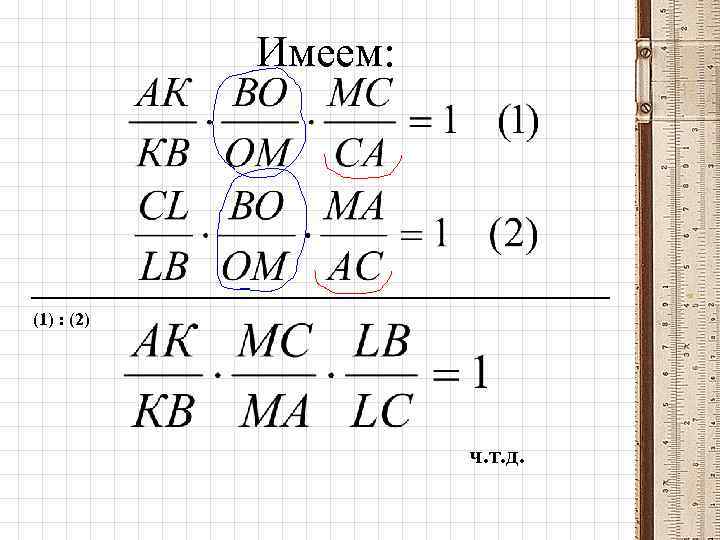Имеем: (1) : (2) ч. т. д.

Задачи по теме

1. Государственный университет управления (Москва): • В трапеции АВСД точка М лежит на боковой стороне АВ, О – пересечение диагонали ВД и отрезка СМ. Найдите площадь треугольника ВОС, если ВМ = 2 АМ, СО = 5 ОМ, а SΔСОД = 1.

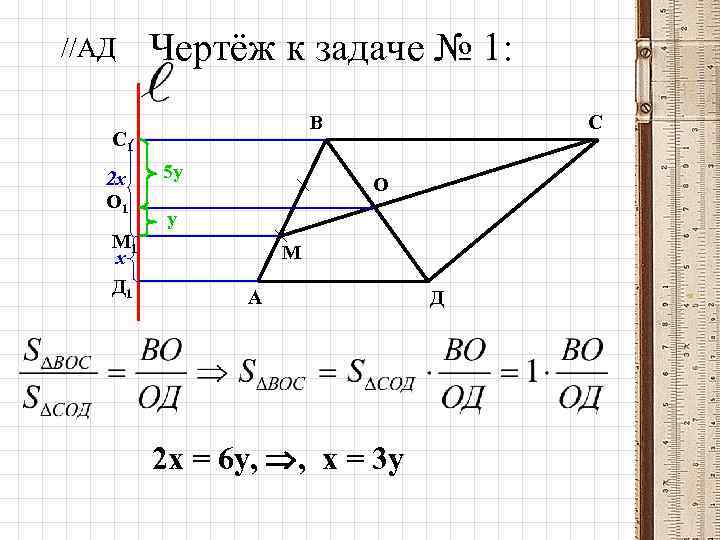//АД Чертёж к задаче № 1: В С 1 2 х О 1 М 1 х Д 1 5 у С О у М А 2 х = 6 у, , х = 3 у Д

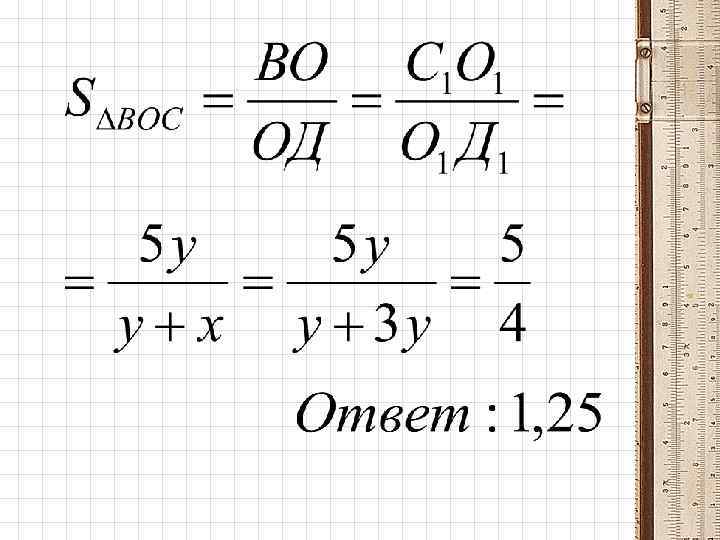
2. Государственный университет управления (Москва): Точки F и N делят стороны ΔАВС в отношении FА : FС = 3 : 1 и СN : NВ = 2 : 3. Прямые АN и ВF пересекаются в точке М. Найдите отношение площадей треугольников АМВ и АNВ.

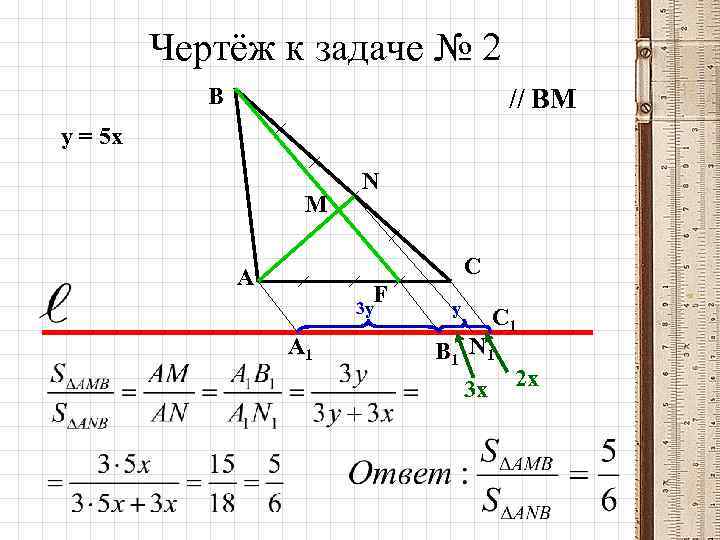Чертёж к задаче № 2 В // ВМ у = 5 х М N С А F 3 у А 1 у С 1 В 1 N 1 3 х 2 х

3. Государственный университет управления (Москва): Прямая, проведённая через вершину А трапеции АВСЕ, пересекает диагональ ВЕ и боковую сторону СЕ в точках Р и К соответственно. Известно что АВ : ВС = 3, СК : КЕ = 2. Найдите отношение площадей треугольников АРЕ и КРЕ.

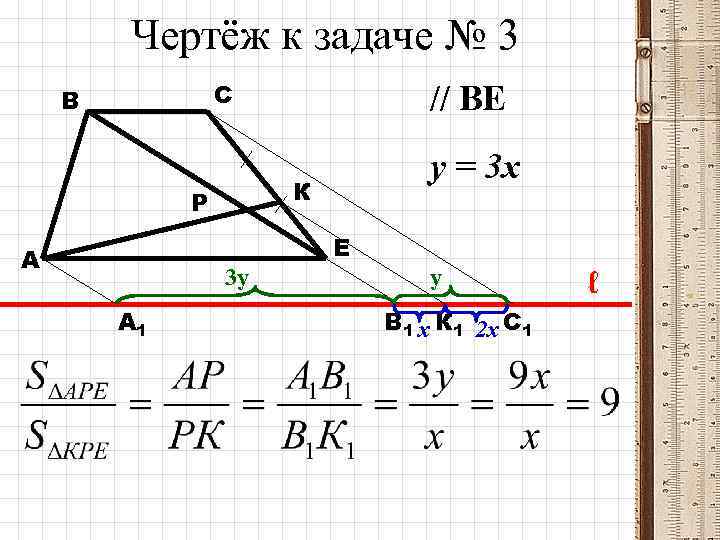Чертёж к задаче № 3 С В // ВЕ у = 3 х К Р Е А 3 у А 1 у В 1 х К 1 2 х С 1 ℓ

4. МГУ, биофак Площадь трапеции АВСД (ВС // АД) равна 30, Р АВ, АР = РВ, R СД, RД = СД, АД = 2 ВС. Найдите площадь треугольника АРQ, где Q = АR РД.

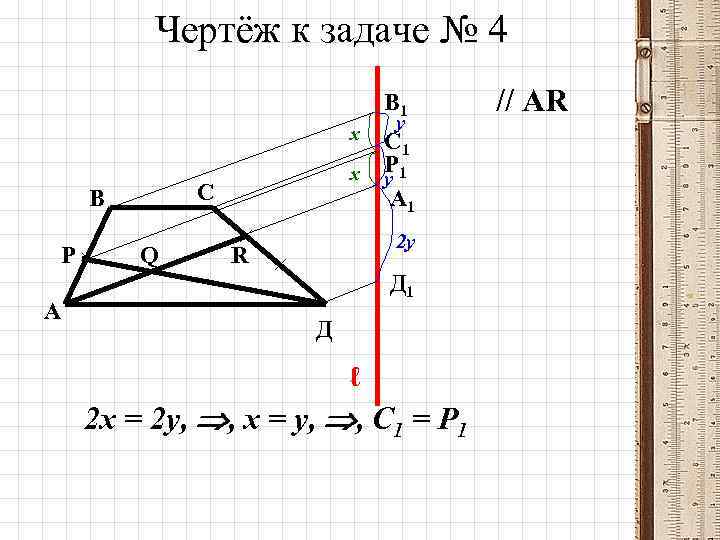Чертёж к задаче № 4 В 1 х С В Р А х Q у С 1 Р 1 у А 1 2 у R Д 1 Д ℓ 2 х = 2 у, , х = у, , С 1 = Р 1 // АR

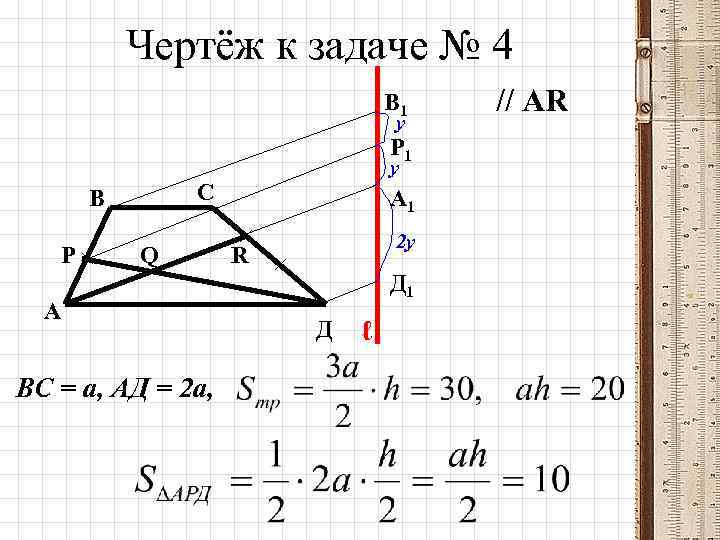Чертёж к задаче № 4 В 1 у Р 1 у С В Р Q А ВС = а, АД = 2 а, А 1 2 у R Д 1 Д ℓ // АR

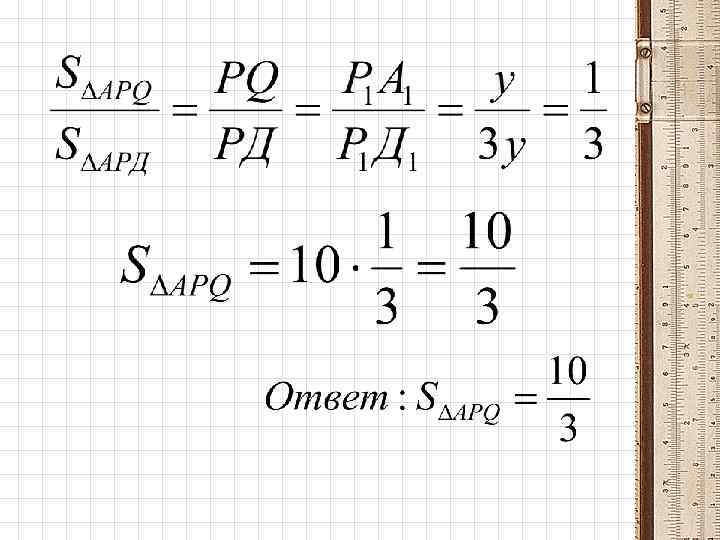
5. МГУ, химфак В треугольнике АВС, АВ = ВС = 8, АС = 6, Е АВ, Д ВС, АЕ = 2, СД = 1, АД СЕ = О. Найдите площадь четырёхугольника ЕВДО.

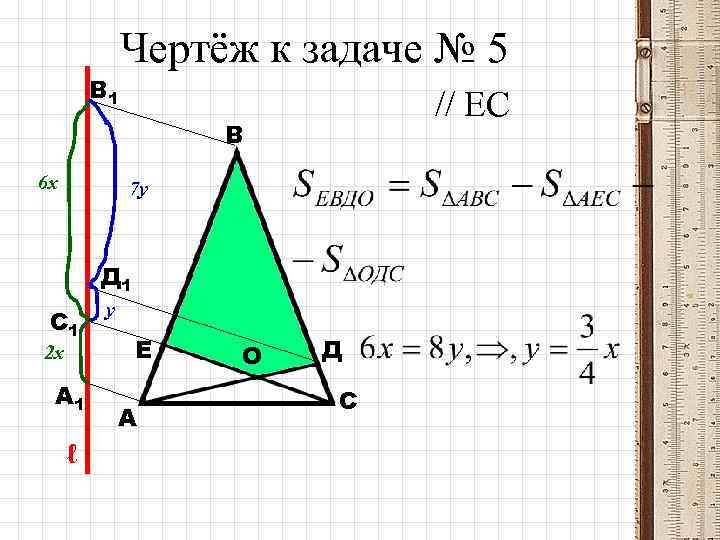В 1 Чертёж к задаче № 5 // ЕС В 6 х 7 у Д 1 С 1 2 х А 1 ℓ у Е А О Д С

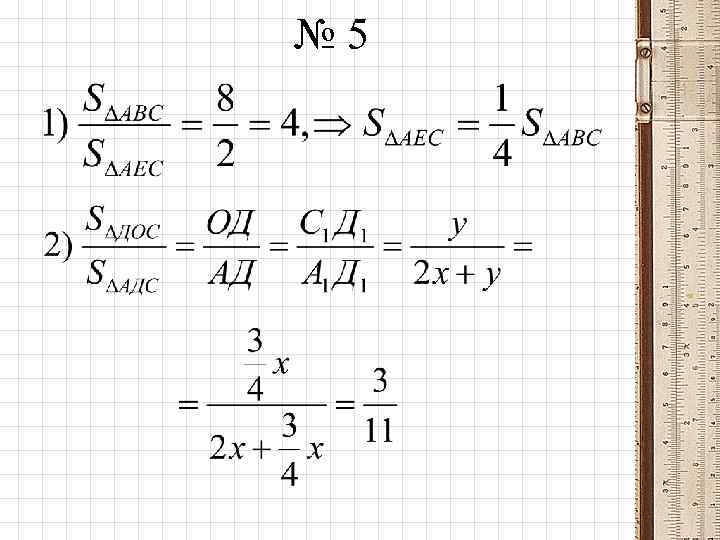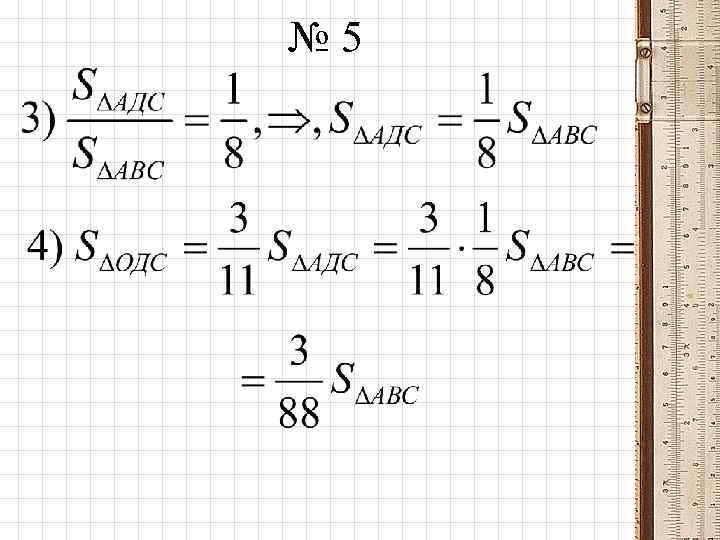№ 5

№ 5

№ 6, МГУ, ф-т почвоведения

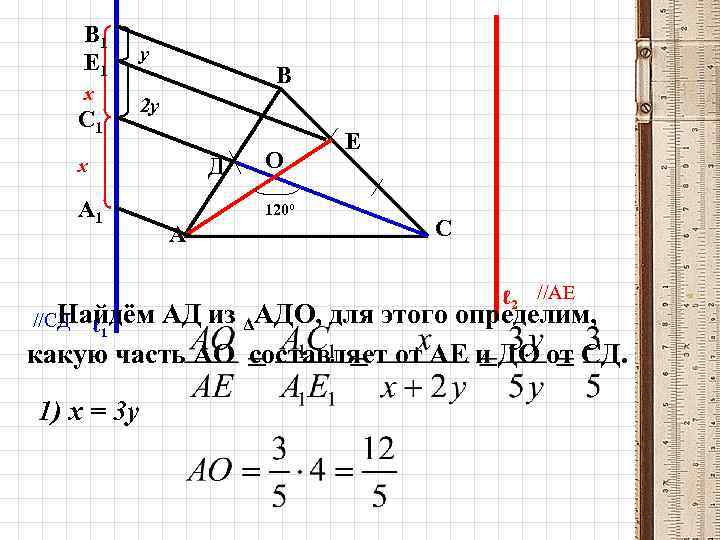В 1 Е 1 х С 1 у В 2 у Д х А 1 Найдём //СД ℓ О 120º А Е С ℓ 2 //АЕ АД из ΔАДО, для этого определим, 1 какую часть АО составляет от АЕ и ДО от СД. 1) х = 3 у

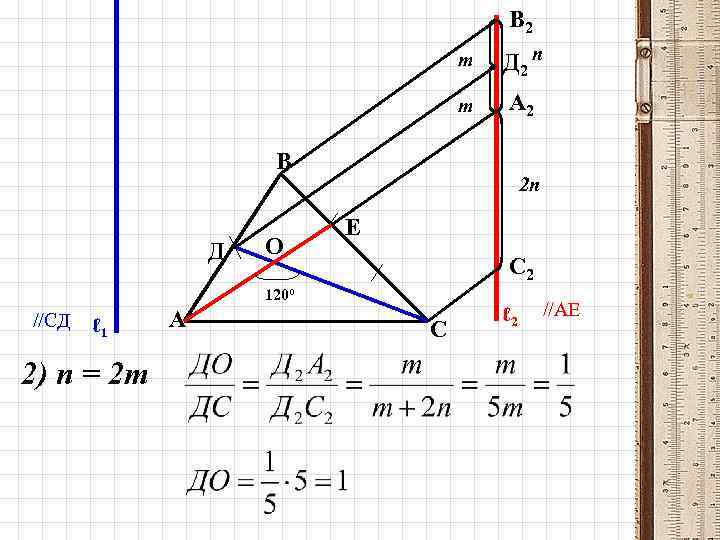В 2 m Д 2 n m А 2 В Д О 2 n Е С 2 120º //СД ℓ 1 2) n = 2 m А С ℓ 2 //АЕ

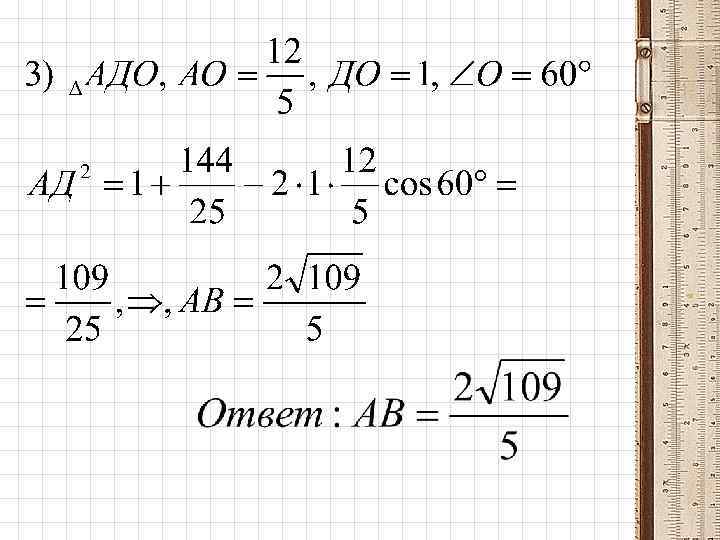
№ 7. МГУ Точки Р и Q расположены на стороне ВС треугольника АВС так, что ВР : РQ : QС =1 : 2 : 3. Точка R делит сторону АС этого треугольника таким образом, что АR : RС = 1 : 2. Чему равно отношение площади четырёхугольника РQSТ к площади треугольника АВС, где S и Т – точки пересечения прямой ВR с прямыми АQ и АР соответственно?

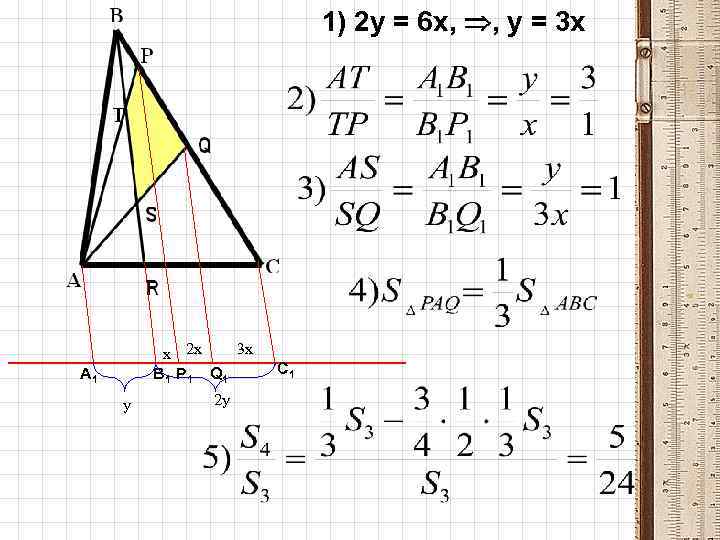1) 2 y = 6 x, , y = 3 x 3 x x 2 x В 1 Р 1 Q 1 А 1 y 2 y C 1

ФИЗКУЛЬТМИНУТКА

ФИЗКУЛЬТМИНУТКА

ФИЗКУЛЬТМИНУТКА