Particle Identification u u d E dx measurement p

Particle Identification u u d. E/dx measurement p K Time of flight p m u Cherenkov detectors u Transition radiation detectors CERN Summer Student Lectures 2003 Particle Detectors Christian Joram

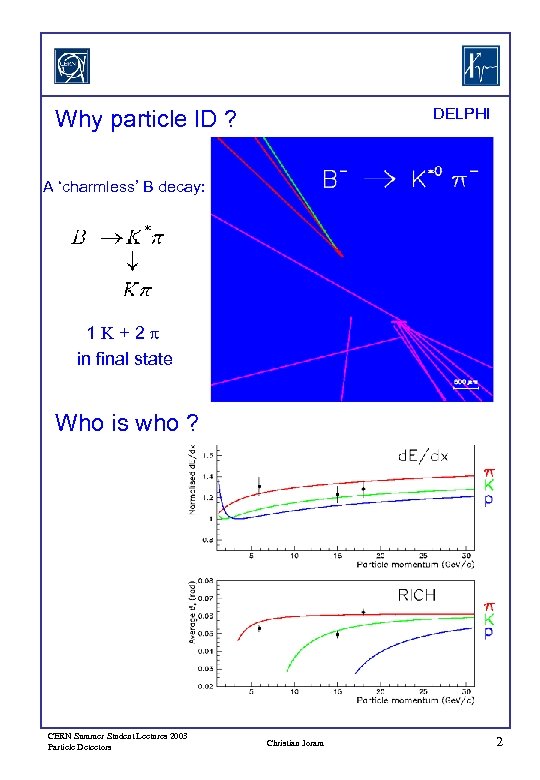DELPHI Why particle ID ? A ‘charmless’ B decay: 1 K+2 p in final state Who is who ? CERN Summer Student Lectures 2003 Particle Detectors Christian Joram 2

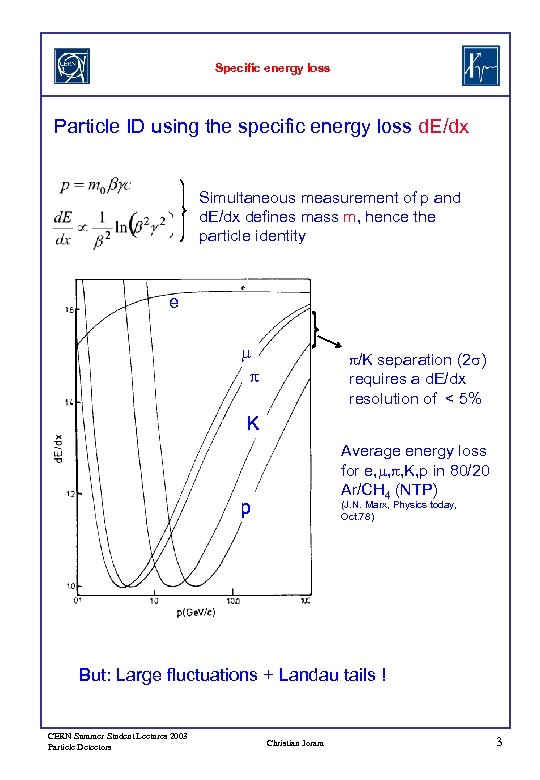Specific energy loss Particle ID using the specific energy loss d. E/dx Simultaneous measurement of p and d. E/dx defines mass m, hence the particle identity e m p p/K separation (2 s) requires a d. E/dx resolution of < 5% K Average energy loss for e, m, p, K, p in 80/20 Ar/CH 4 (NTP) p (J. N. Marx, Physics today, Oct. 78) But: Large fluctuations + Landau tails ! CERN Summer Student Lectures 2003 Particle Detectors Christian Joram 3

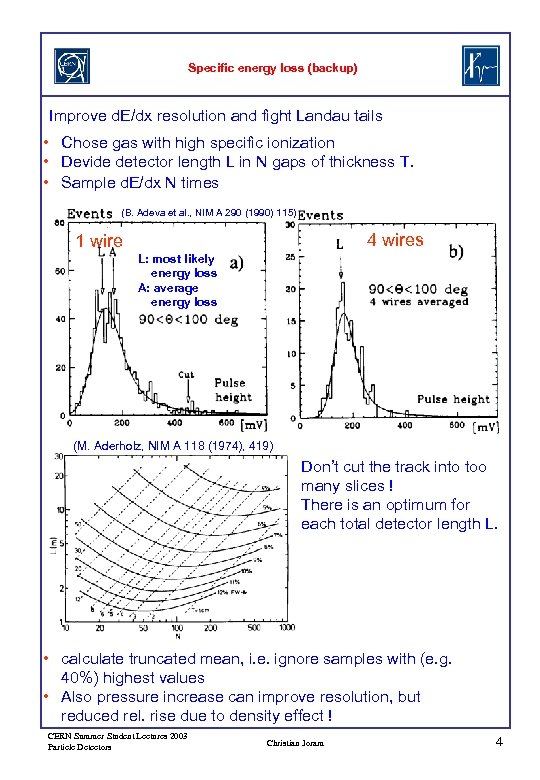Specific energy loss (backup) Improve d. E/dx resolution and fight Landau tails • Chose gas with high specific ionization • Devide detector length L in N gaps of thickness T. • Sample d. E/dx N times (B. Adeva et al. , NIM A 290 (1990) 115) 4 wires 1 wire L: most likely energy loss A: average energy loss (M. Aderholz, NIM A 118 (1974), 419) Don’t cut the track into too many slices ! There is an optimum for each total detector length L. • calculate truncated mean, i. e. ignore samples with (e. g. 40%) highest values • Also pressure increase can improve resolution, but reduced rel. rise due to density effect ! CERN Summer Student Lectures 2003 Particle Detectors Christian Joram 4

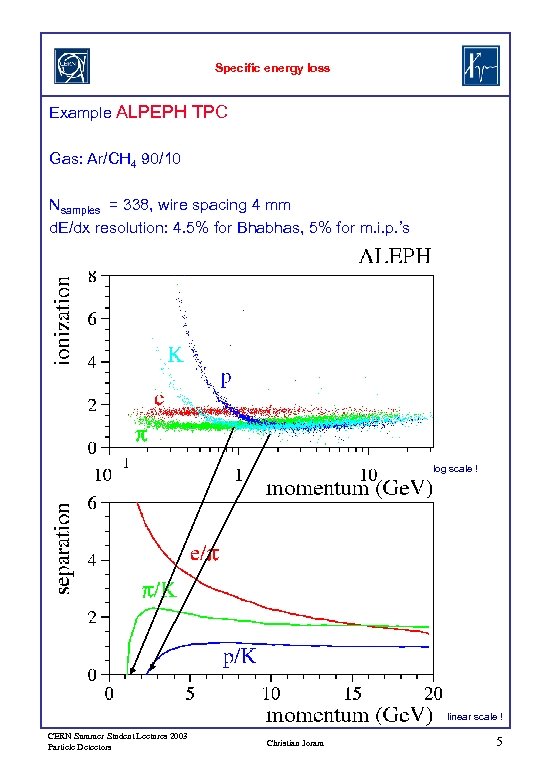Specific energy loss Example ALPEPH TPC Gas: Ar/CH 4 90/10 Nsamples = 338, wire spacing 4 mm d. E/dx resolution: 4. 5% for Bhabhas, 5% for m. i. p. ’s log scale ! linear scale ! CERN Summer Student Lectures 2003 Particle Detectors Christian Joram 5

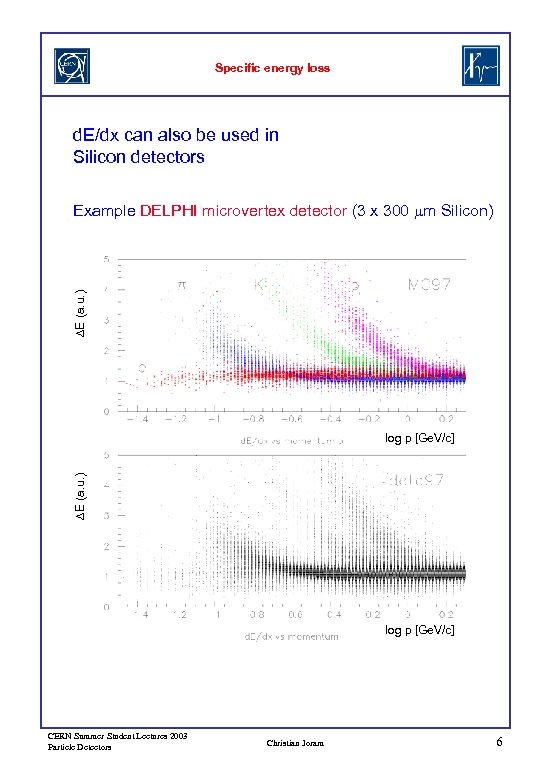Specific energy loss d. E/dx can also be used in Silicon detectors DE (a. u. ) Example DELPHI microvertex detector (3 x 300 mm Silicon) DE (a. u. ) log p [Ge. V/c] CERN Summer Student Lectures 2003 Particle Detectors Christian Joram 6

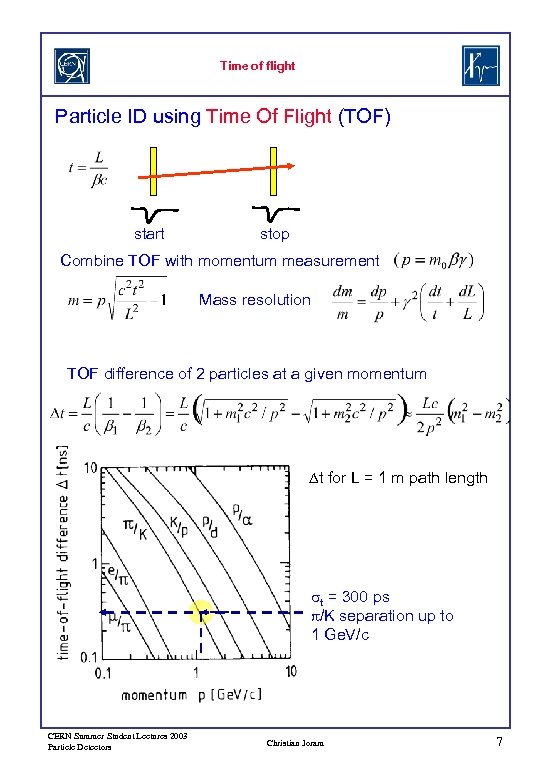Time of flight Particle ID using Time Of Flight (TOF) start stop Combine TOF with momentum measurement Mass resolution TOF difference of 2 particles at a given momentum Dt for L = 1 m path length st = 300 ps p/K separation up to 1 Ge. V/c CERN Summer Student Lectures 2003 Particle Detectors Christian Joram 7

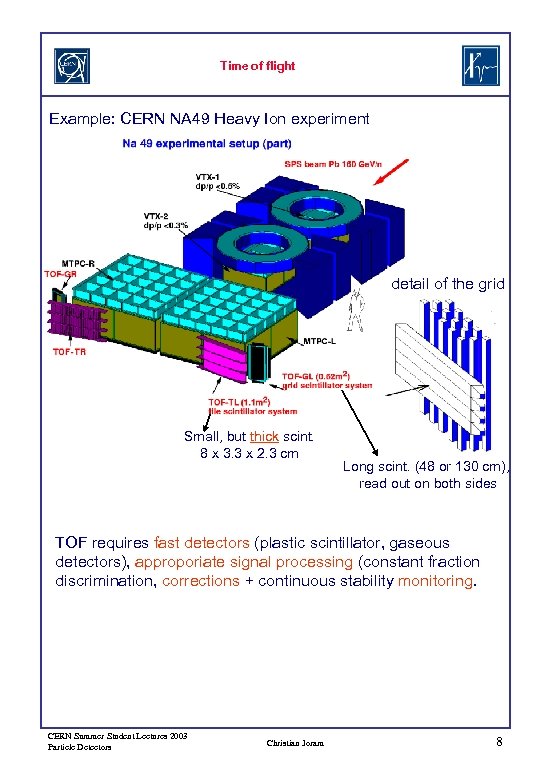Time of flight Example: CERN NA 49 Heavy Ion experiment detail of the grid Small, but thick scint. 8 x 3. 3 x 2. 3 cm Long scint. (48 or 130 cm), read out on both sides TOF requires fast detectors (plastic scintillator, gaseous detectors), approporiate signal processing (constant fraction discrimination, corrections + continuous stability monitoring. CERN Summer Student Lectures 2003 Particle Detectors Christian Joram 8

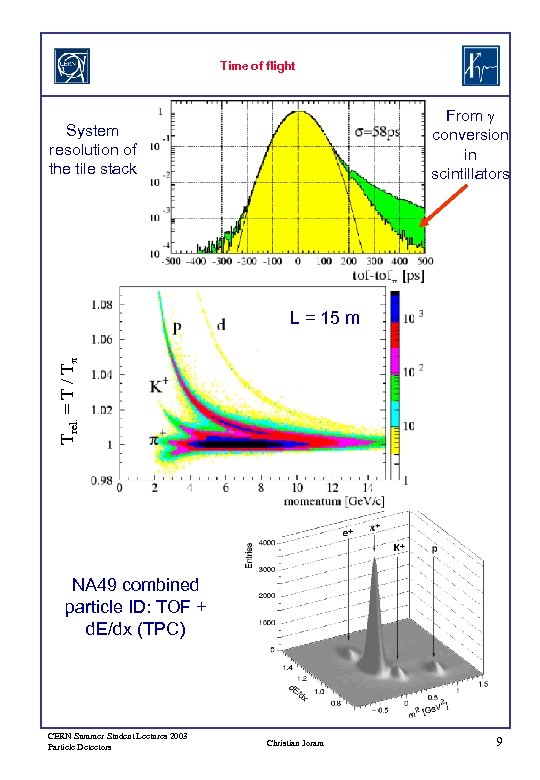Time of flight From g conversion in scintillators System resolution of the tile stack Trel. = T / Tp L = 15 m NA 49 combined particle ID: TOF + d. E/dx (TPC) CERN Summer Student Lectures 2003 Particle Detectors Christian Joram 9

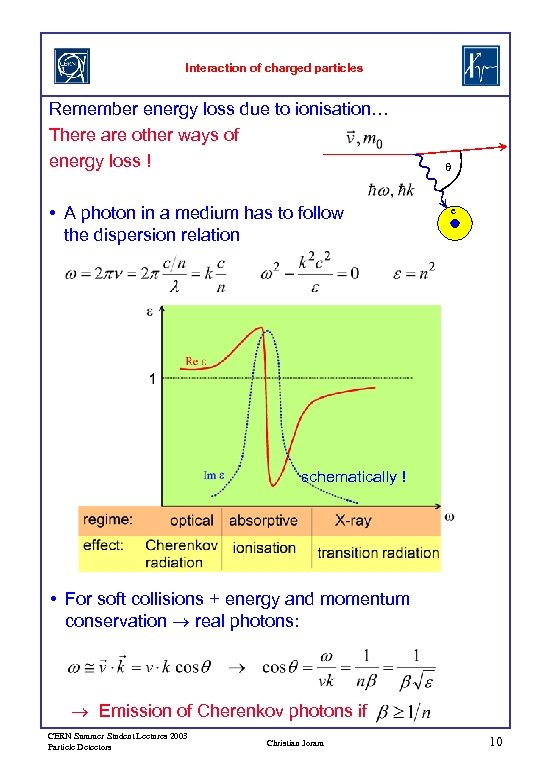Interaction of charged particles Remember energy loss due to ionisation… There are other ways of energy loss ! • A photon in a medium has to follow the dispersion relation q e schematically ! • For soft collisions + energy and momentum conservation real photons: Emission of Cherenkov photons if CERN Summer Student Lectures 2003 Particle Detectors Christian Joram 10

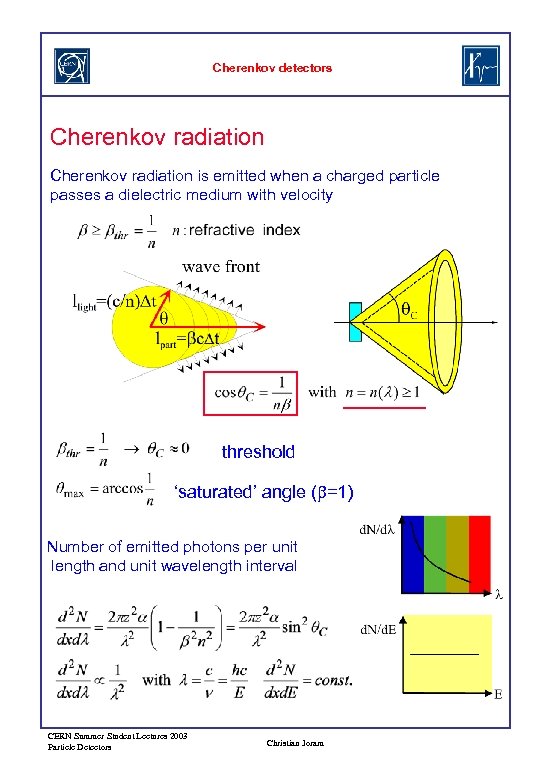Cherenkov detectors Cherenkov radiation is emitted when a charged particle passes a dielectric medium with velocity threshold ‘saturated’ angle (b=1) Number of emitted photons per unit length and unit wavelength interval CERN Summer Student Lectures 2003 Particle Detectors Christian Joram

Cherenkov detectors Energy loss by Cherenkov radiation small compared to ionization ( 1%) Number of detected photo electrons DE = E 2 - E 1 is the width of the sensitive window of the photodetector (photomultiplier, photosensitive gas detector. . . ) Example: for a detector with and a Cherenkov angle of one expects photo electrons CERN Summer Student Lectures 2003 Particle Detectors Christian Joram

Cherenkov detectors Particle ID with Cherenkov detectors Detectors can exploit. . . • • (do not measure q. C) Nph(b): threshold detector q(b): differential and Ring Imaging Cherenkov detectors “RICH” Threshold Cherenkov detectors principle Goal: p/K separation bkaon Example: study of an Aerogel threshold detector for the BELLE experiment at KEK (Japan) CERN Summer Student Lectures 2003 Particle Detectors Christian Joram

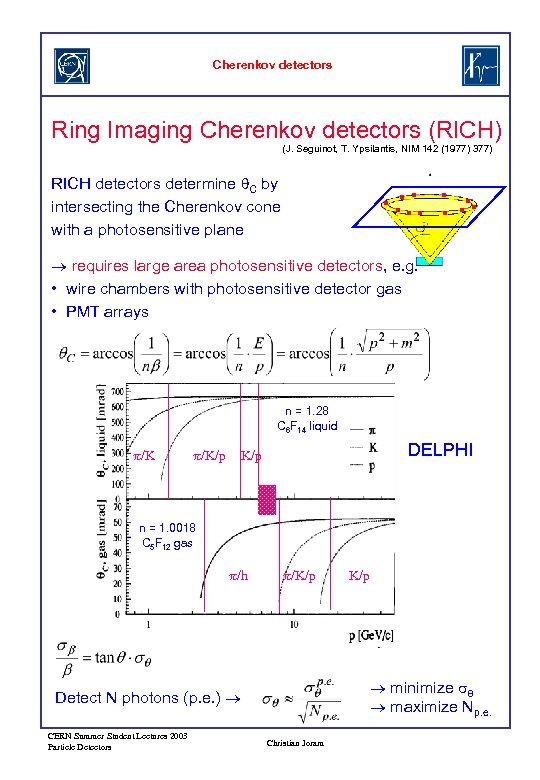Cherenkov detectors Ring Imaging Cherenkov detectors (RICH) (J. Seguinot, T. Ypsilantis, NIM 142 (1977) 377) . . . RICH detectors determine q. C by intersecting the Cherenkov cone with a photosensitive plane requires large area photosensitive detectors, e. g. • wire chambers with photosensitive detector gas • PMT arrays n = 1. 28 C 6 F 14 liquid p/K/p DELPHI K/p n = 1. 0018 C 5 F 12 gas p/h p/K/p minimize sq maximize Np. e. Detect N photons (p. e. ) CERN Summer Student Lectures 2003 Particle Detectors K/p Christian Joram

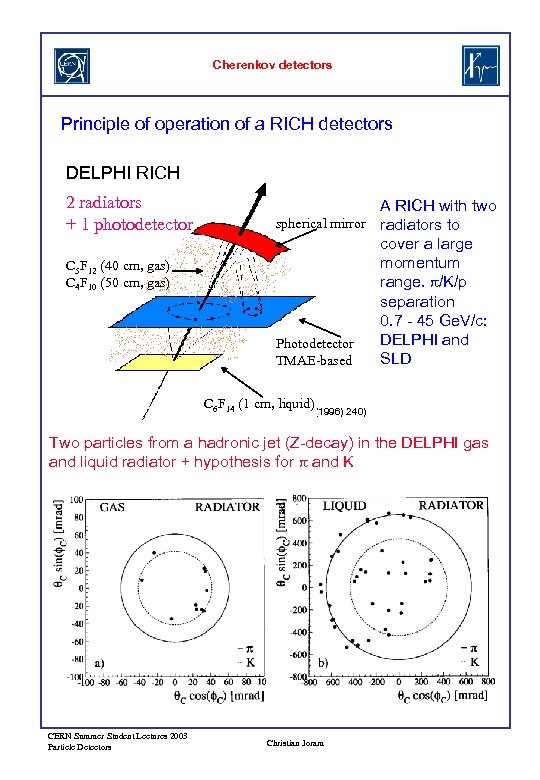Cherenkov detectors Principle of operation of a RICH detectors DELPHI RICH 2 radiators + 1 photodetector C 5 F 12 (40 cm, gas) C 4 F 10 (50 cm, gas) A RICH with two spherical mirror radiators to cover a large momentum range. p/K/p separation 0. 7 - 45 Ge. V/c: DELPHI and Photodetector SLD TMAE-based C F (1 cm, liquid) 6 14 (W. Adam et al. NIM A 371 (1996) 240) Two particles from a hadronic jet (Z-decay) in the DELPHI gas and liquid radiator + hypothesis for p and K CERN Summer Student Lectures 2003 Particle Detectors Christian Joram

Cherenkov detectors The mirror cage of the DELPHI Barrel RICH (288 parabolic mirrors) CERN Summer Student Lectures 2003 Particle Detectors Christian Joram

Cherenkov detectors “Marriage” of mirror cage and central detector part of the DELPHI Barrel RICH. CERN Summer Student Lectures 2003 Particle Detectors Christian Joram

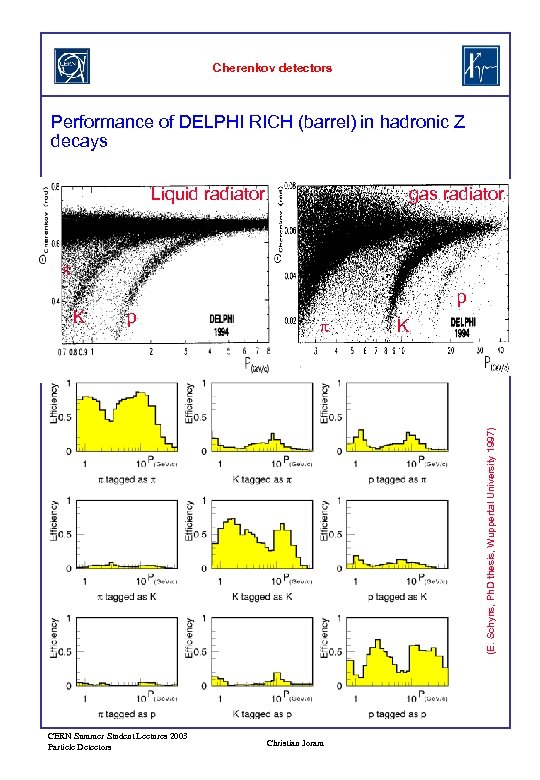Cherenkov detectors Performance of DELPHI RICH (barrel) in hadronic Z decays Liquid radiator gas radiator p p p K (E. Schyns, Ph. D thesis, Wuppertal University 1997) K p CERN Summer Student Lectures 2003 Particle Detectors Christian Joram

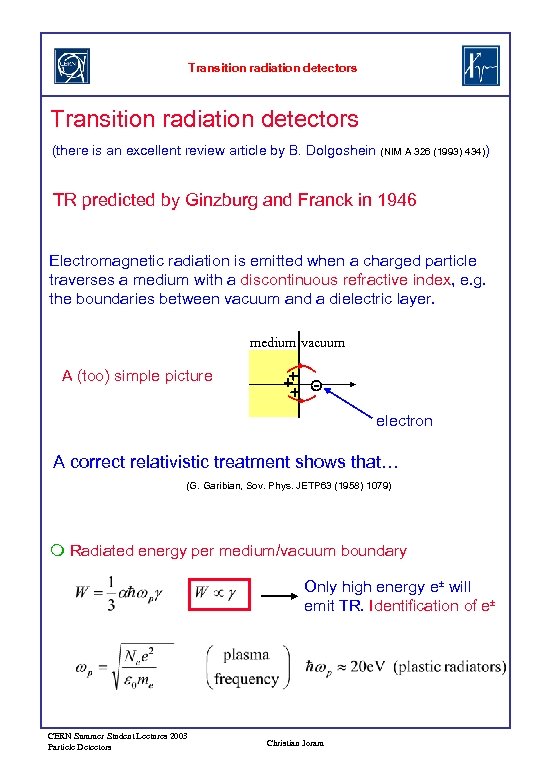Transition radiation detectors (there is an excellent review article by B. Dolgoshein (NIM A 326 (1993) 434)) TR predicted by Ginzburg and Franck in 1946 Electromagnetic radiation is emitted when a charged particle traverses a medium with a discontinuous refractive index, e. g. the boundaries between vacuum and a dielectric layer. medium vacuum A (too) simple picture electron A correct relativistic treatment shows that… (G. Garibian, Sov. Phys. JETP 63 (1958) 1079) Radiated energy per medium/vacuum boundary Only high energy e± will emit TR. Identification of e± CERN Summer Student Lectures 2003 Particle Detectors Christian Joram

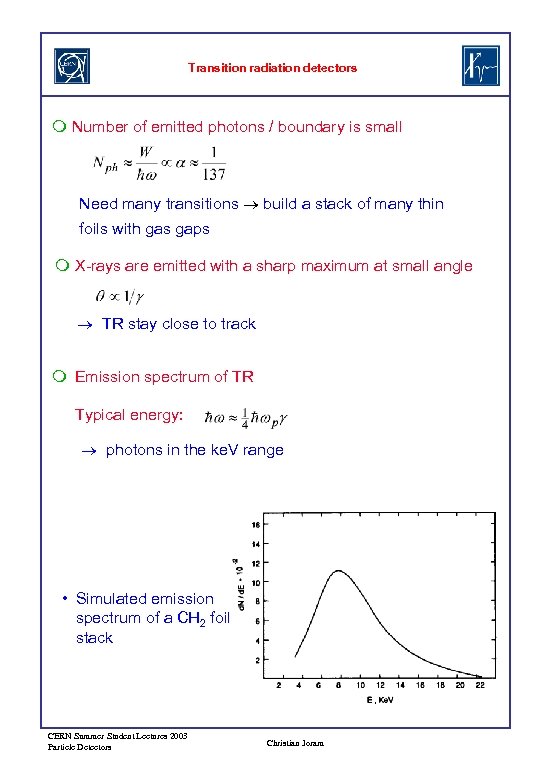Transition radiation detectors Number of emitted photons / boundary is small Need many transitions build a stack of many thin foils with gas gaps X-rays are emitted with a sharp maximum at small angle TR stay close to track Emission spectrum of TR Typical energy: photons in the ke. V range • Simulated emission spectrum of a CH 2 foil stack CERN Summer Student Lectures 2003 Particle Detectors Christian Joram

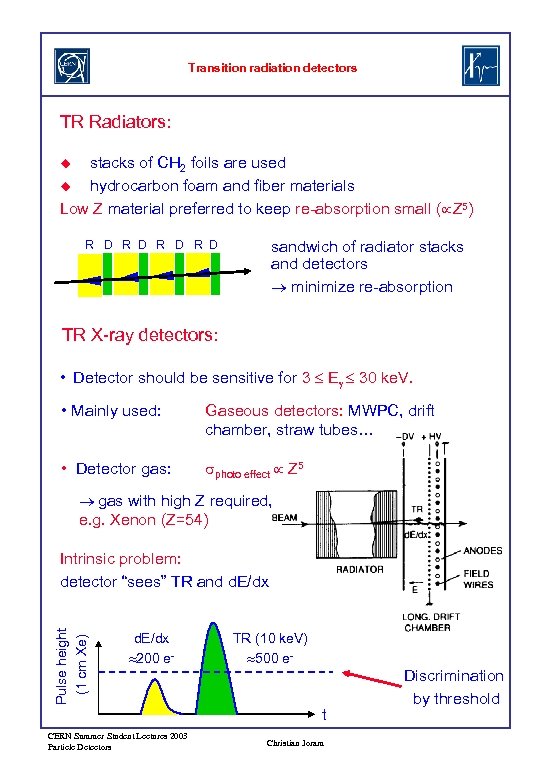Transition radiation detectors TR Radiators: stacks of CH 2 foils are used u hydrocarbon foam and fiber materials Low Z material preferred to keep re-absorption small ( Z 5) u sandwich of radiator stacks and detectors minimize re-absorption R D R D TR X-ray detectors: • Detector should be sensitive for 3 Eg 30 ke. V. • Mainly used: Gaseous detectors: MWPC, drift chamber, straw tubes… • Detector gas: sphoto effect Z 5 gas with high Z required, e. g. Xenon (Z=54) Pulse height (1 cm Xe) Intrinsic problem: detector “sees” TR and d. E/dx 200 e- TR (10 ke. V) 500 e- t CERN Summer Student Lectures 2003 Particle Detectors Christian Joram Discrimination by threshold

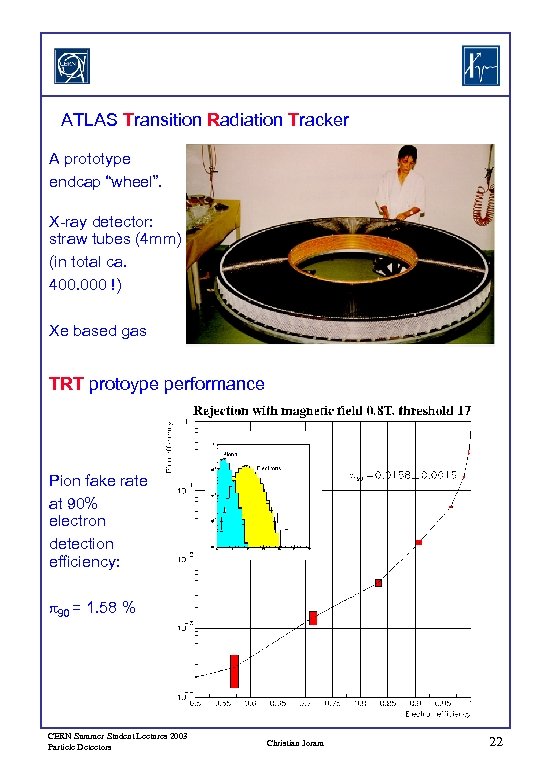ATLAS Transition Radiation Tracker A prototype endcap “wheel”. X-ray detector: straw tubes (4 mm) (in total ca. 400. 000 !) Xe based gas TRT protoype performance Pion fake rate at 90% electron detection efficiency: p 90 = 1. 58 % CERN Summer Student Lectures 2003 Particle Detectors Christian Joram 22

Particle Identification Summary: u u A number of powerful methods are available to identify particles over a large momentum range. Depending on the available space and the environment, the identification power can vary significantly. A very coarse plot …. e± identification p/K separation CERN Summer Student Lectures 2003 Particle Detectors Christian Joram

Detector Systems Let’s find some tools … and put everything together ! CERN Summer Student Lectures 2003 Particle Detectors Christian Joram 24

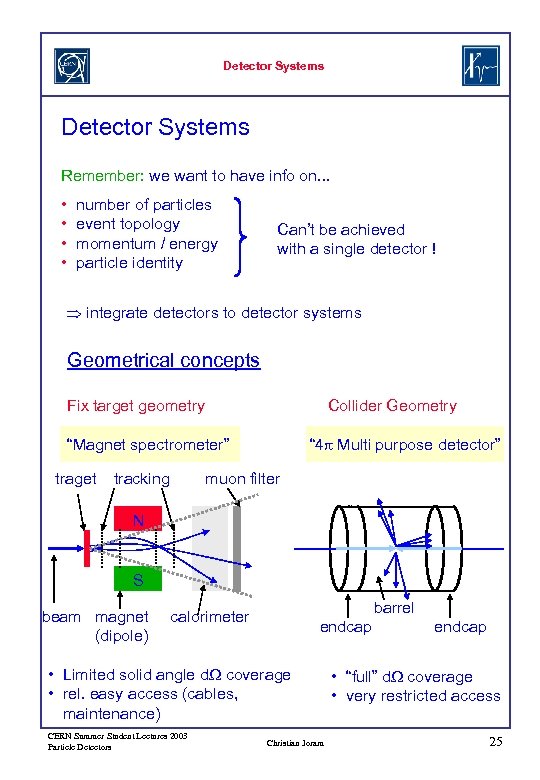Detector Systems Remember: we want to have info on. . . • • number of particles event topology momentum / energy particle identity Can’t be achieved with a single detector ! integrate detectors to detector systems Geometrical concepts Fix target geometry Collider Geometry “Magnet spectrometer” traget tracking “ 4 p Multi purpose detector” muon filter N S beam magnet (dipole) barrel calorimeter endcap • Limited solid angle d. W coverage • rel. easy access (cables, maintenance) CERN Summer Student Lectures 2003 Particle Detectors Christian Joram endcap • “full” d. W coverage • very restricted access 25

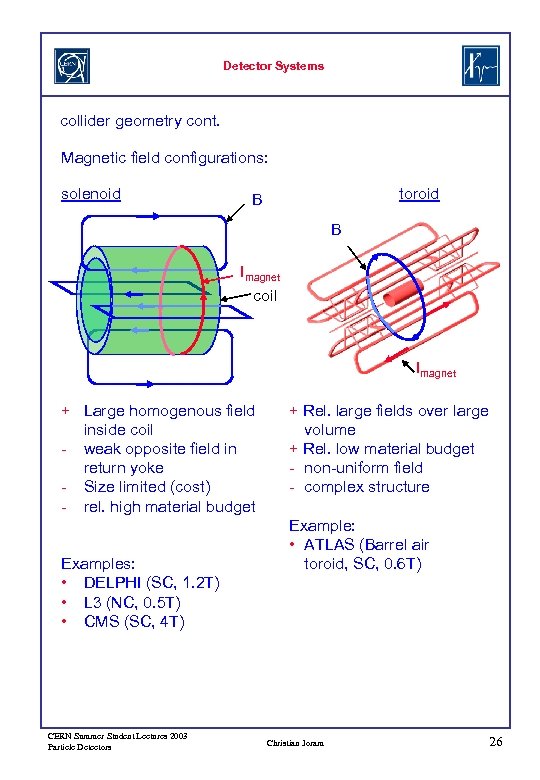Detector Systems collider geometry cont. Magnetic field configurations: solenoid toroid B B Imagnet coil Imagnet + Large homogenous field inside coil - weak opposite field in return yoke - Size limited (cost) - rel. high material budget Examples: • DELPHI (SC, 1. 2 T) • L 3 (NC, 0. 5 T) • CMS (SC, 4 T) CERN Summer Student Lectures 2003 Particle Detectors + Rel. large fields over large volume + Rel. low material budget - non-uniform field - complex structure Example: • ATLAS (Barrel air toroid, SC, 0. 6 T) Christian Joram 26

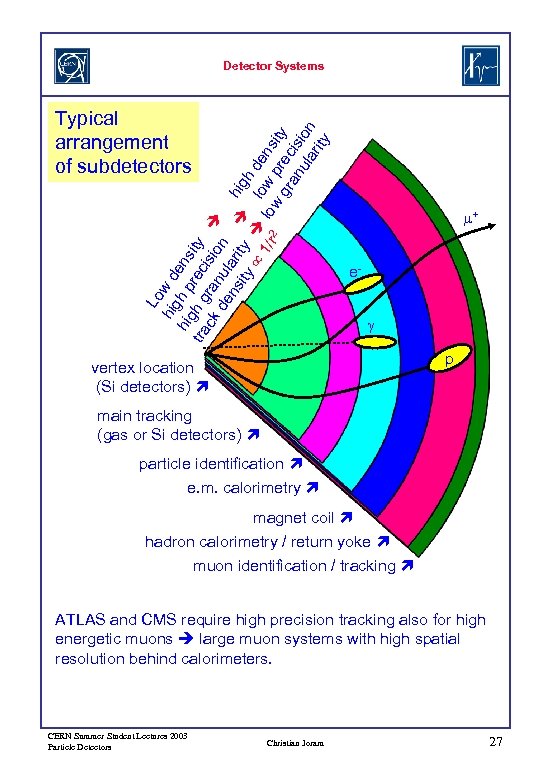Detector Systems Lo hig w d hig h p ens tra h g rec ity ck ra isio de nul n ns ari ity ty high d 1/ 2 lo low ens r w p gr rec ity an is ula ion rit y Typical arrangement of subdetectors m+ eg p vertex location (Si detectors) main tracking (gas or Si detectors) particle identification e. m. calorimetry magnet coil hadron calorimetry / return yoke muon identification / tracking ATLAS and CMS require high precision tracking also for high energetic muons large muon systems with high spatial resolution behind calorimeters. CERN Summer Student Lectures 2003 Particle Detectors Christian Joram 27

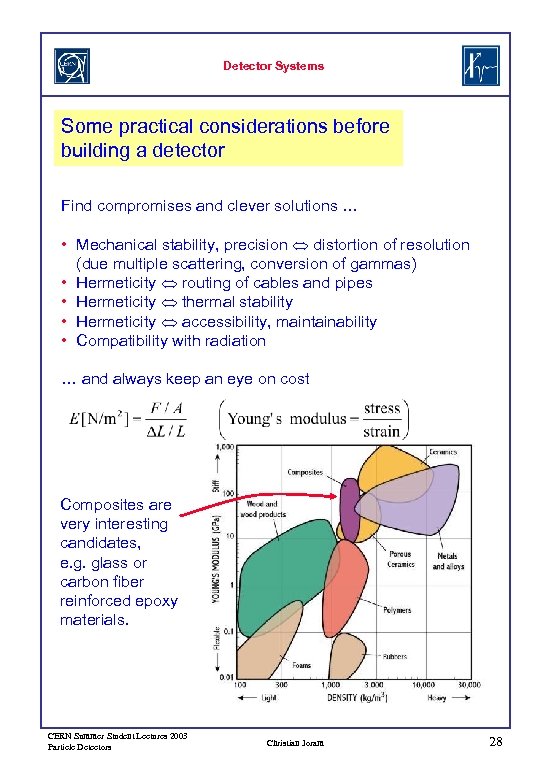Detector Systems Some practical considerations before building a detector Find compromises and clever solutions … • Mechanical stability, precision distortion of resolution (due multiple scattering, conversion of gammas) • Hermeticity routing of cables and pipes • Hermeticity thermal stability • Hermeticity accessibility, maintainability • Compatibility with radiation … and always keep an eye on cost Composites are very interesting candidates, e. g. glass or carbon fiber reinforced epoxy materials. CERN Summer Student Lectures 2003 Particle Detectors Christian Joram 28

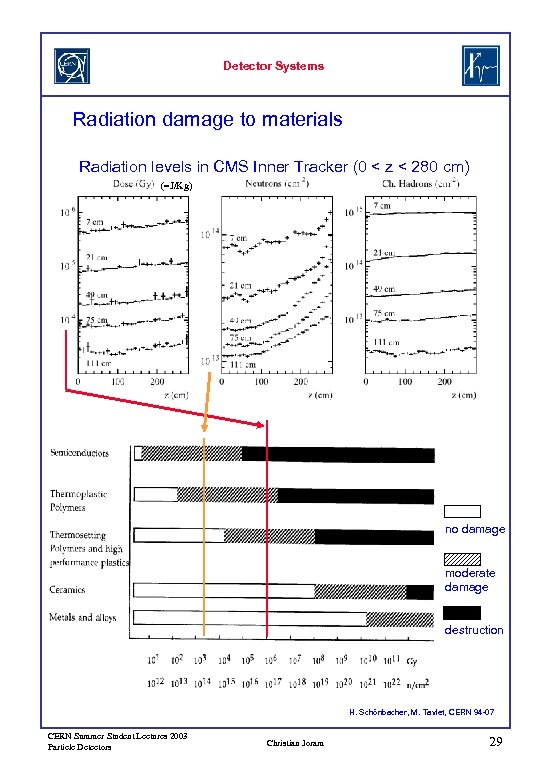Detector Systems Radiation damage to materials Radiation levels in CMS Inner Tracker (0 < z < 280 cm) (=J/Kg) no damage moderate damage destruction H. Schönbacher, M. Tavlet, CERN 94 -07 CERN Summer Student Lectures 2003 Particle Detectors Christian Joram 29

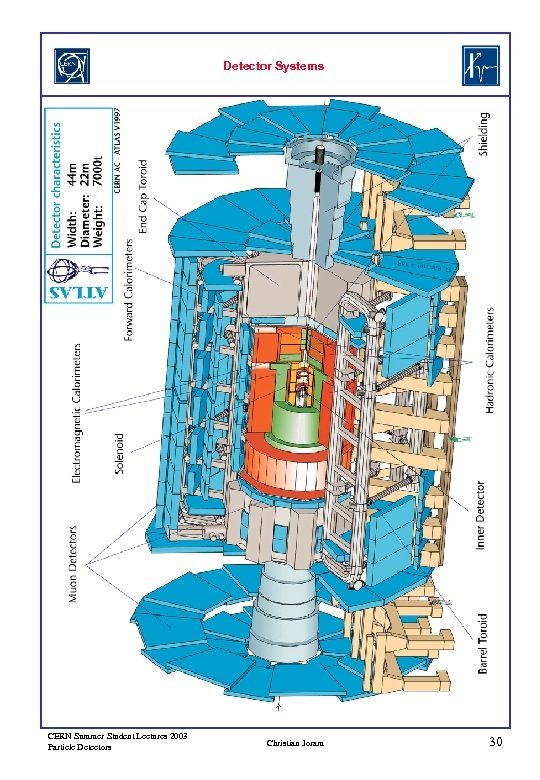Detector Systems CERN Summer Student Lectures 2003 Particle Detectors Christian Joram 30

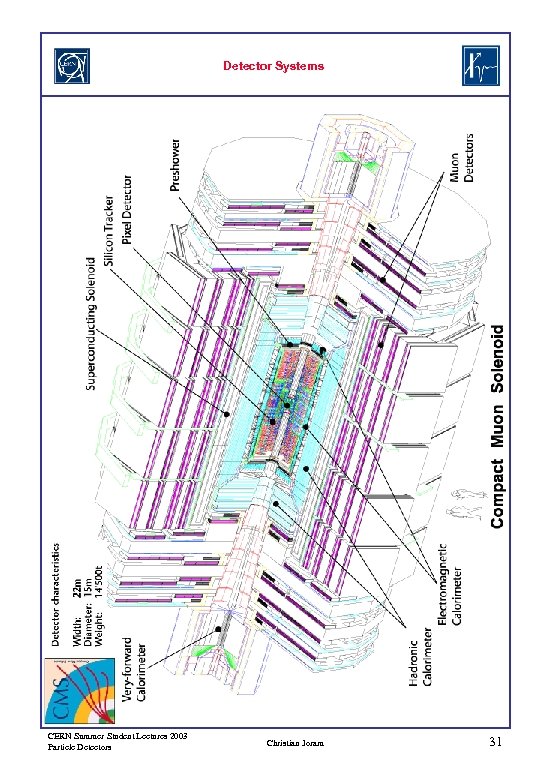Detector Systems CERN Summer Student Lectures 2003 Particle Detectors Christian Joram 31

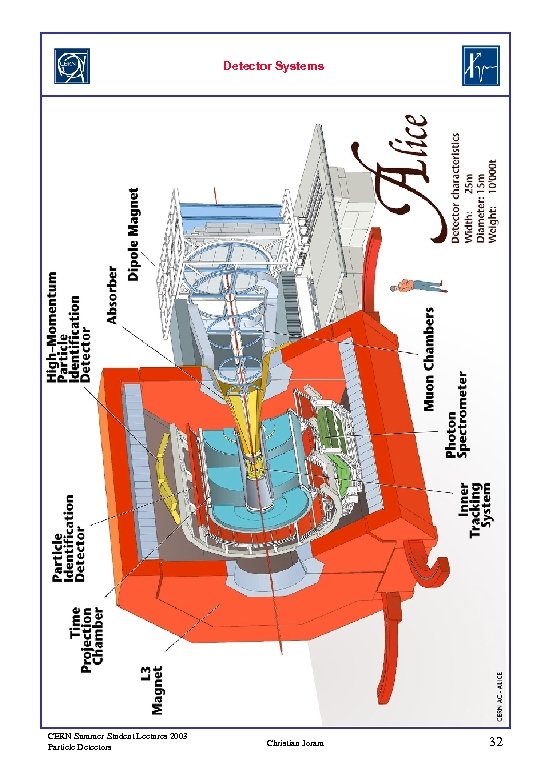Detector Systems CERN Summer Student Lectures 2003 Particle Detectors Christian Joram 32

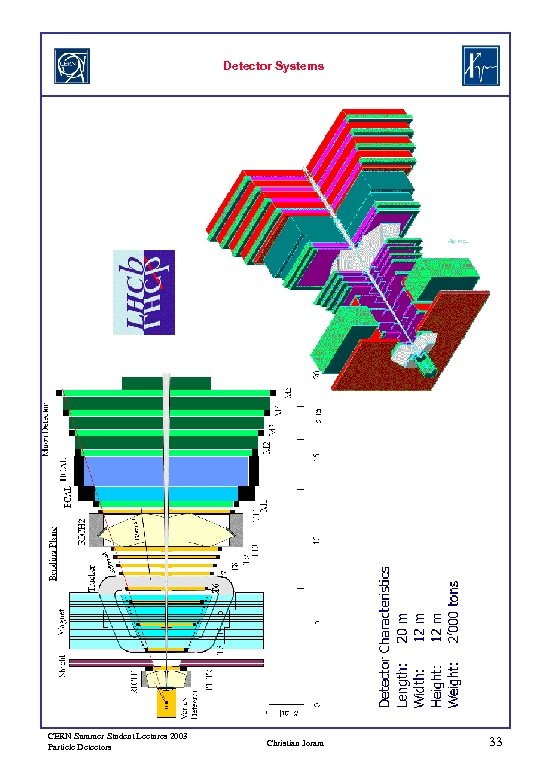Detector Systems CERN Summer Student Lectures 2003 Particle Detectors Christian Joram 33