81a9d845429defd023c94711b4729bb2.ppt
- Количество слайдов: 32
 Part Two: Oscillations, Waves, & Fluids Examples of oscillations & waves: Earthquake – Tsunami Electric guitar – Sound wave Watch – quartz crystal Radar speed-trap Radio telescope Examples of fluid High-speed photo: spreading circular waves on water. mechanics: Flow speed vs river width Plane flight
Part Two: Oscillations, Waves, & Fluids Examples of oscillations & waves: Earthquake – Tsunami Electric guitar – Sound wave Watch – quartz crystal Radar speed-trap Radio telescope Examples of fluid High-speed photo: spreading circular waves on water. mechanics: Flow speed vs river width Plane flight
 13. Oscillatory Motion 1. 2. 3. 4. 5. 6. 7. Describing Oscillatory Motion Simple Harmonic Motion Applications of Simple Harmonic Motion Circular & Harmonic Motion Energy in Simple Harmonic Motion Damped Harmonic Motion Driven Oscillations & Resonance
13. Oscillatory Motion 1. 2. 3. 4. 5. 6. 7. Describing Oscillatory Motion Simple Harmonic Motion Applications of Simple Harmonic Motion Circular & Harmonic Motion Energy in Simple Harmonic Motion Damped Harmonic Motion Driven Oscillations & Resonance
 Dancers from the Bandaloop Project perform on vertical surfaces, executing graceful slow-motion jumps. What determines the duration of these jumps? pendulum motion: rope length & g Wilberforce Pendulum
Dancers from the Bandaloop Project perform on vertical surfaces, executing graceful slow-motion jumps. What determines the duration of these jumps? pendulum motion: rope length & g Wilberforce Pendulum
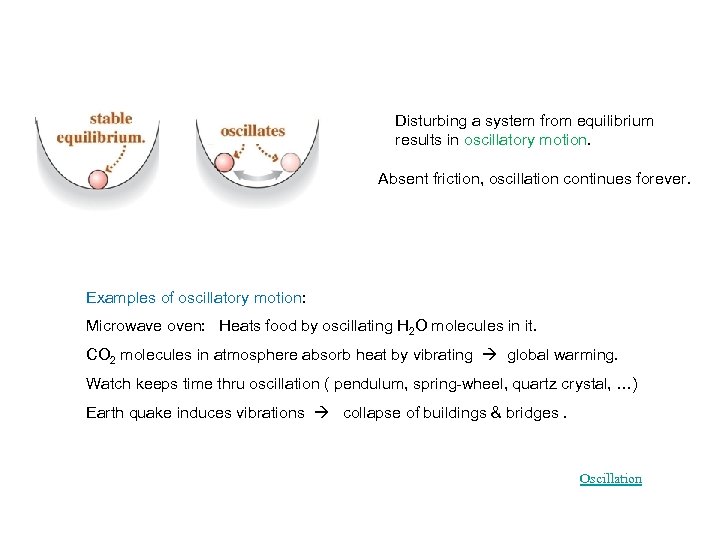 Disturbing a system from equilibrium results in oscillatory motion. Absent friction, oscillation continues forever. Examples of oscillatory motion: Microwave oven: Heats food by oscillating H 2 O molecules in it. CO 2 molecules in atmosphere absorb heat by vibrating global warming. Watch keeps time thru oscillation ( pendulum, spring-wheel, quartz crystal, …) Earth quake induces vibrations collapse of buildings & bridges. Oscillation
Disturbing a system from equilibrium results in oscillatory motion. Absent friction, oscillation continues forever. Examples of oscillatory motion: Microwave oven: Heats food by oscillating H 2 O molecules in it. CO 2 molecules in atmosphere absorb heat by vibrating global warming. Watch keeps time thru oscillation ( pendulum, spring-wheel, quartz crystal, …) Earth quake induces vibrations collapse of buildings & bridges. Oscillation
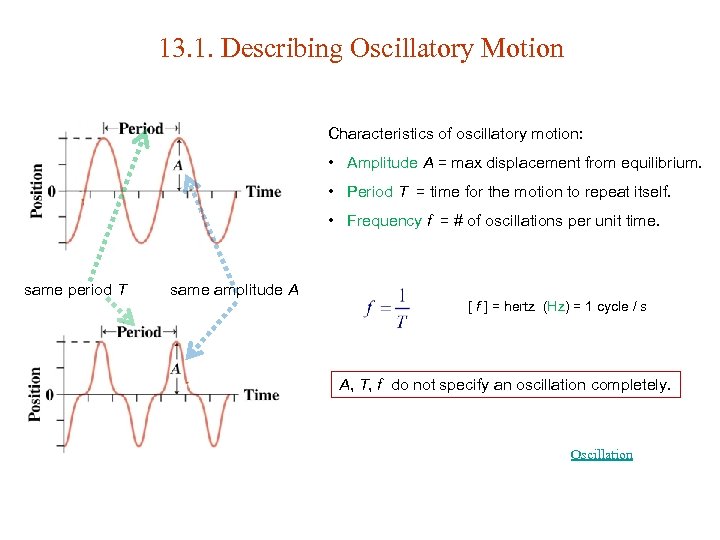 13. 1. Describing Oscillatory Motion Characteristics of oscillatory motion: • Amplitude A = max displacement from equilibrium. • Period T = time for the motion to repeat itself. • Frequency f = # of oscillations per unit time. same period T same amplitude A [ f ] = hertz (Hz) = 1 cycle / s A, T, f do not specify an oscillation completely. Oscillation
13. 1. Describing Oscillatory Motion Characteristics of oscillatory motion: • Amplitude A = max displacement from equilibrium. • Period T = time for the motion to repeat itself. • Frequency f = # of oscillations per unit time. same period T same amplitude A [ f ] = hertz (Hz) = 1 cycle / s A, T, f do not specify an oscillation completely. Oscillation
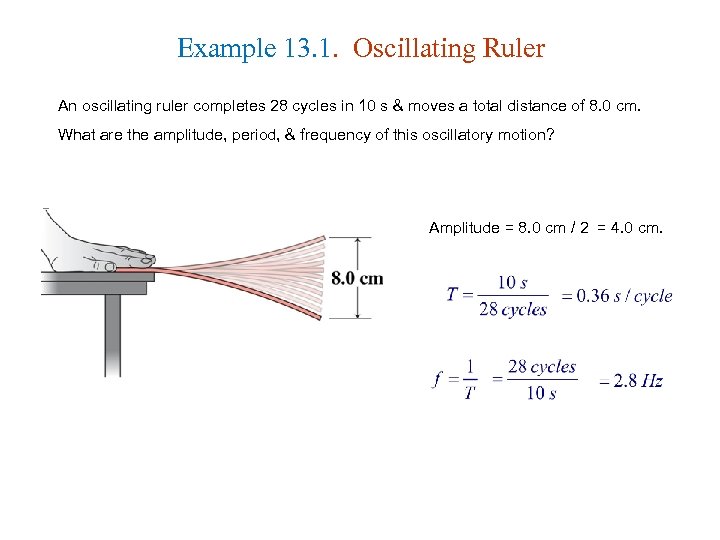 Example 13. 1. Oscillating Ruler An oscillating ruler completes 28 cycles in 10 s & moves a total distance of 8. 0 cm. What are the amplitude, period, & frequency of this oscillatory motion? Amplitude = 8. 0 cm / 2 = 4. 0 cm.
Example 13. 1. Oscillating Ruler An oscillating ruler completes 28 cycles in 10 s & moves a total distance of 8. 0 cm. What are the amplitude, period, & frequency of this oscillatory motion? Amplitude = 8. 0 cm / 2 = 4. 0 cm.
 13. 2. Simple Harmonic Motion (SHM): 2 nd order diff. eq 2 integration const. Ansatz: angular frequency
13. 2. Simple Harmonic Motion (SHM): 2 nd order diff. eq 2 integration const. Ansatz: angular frequency
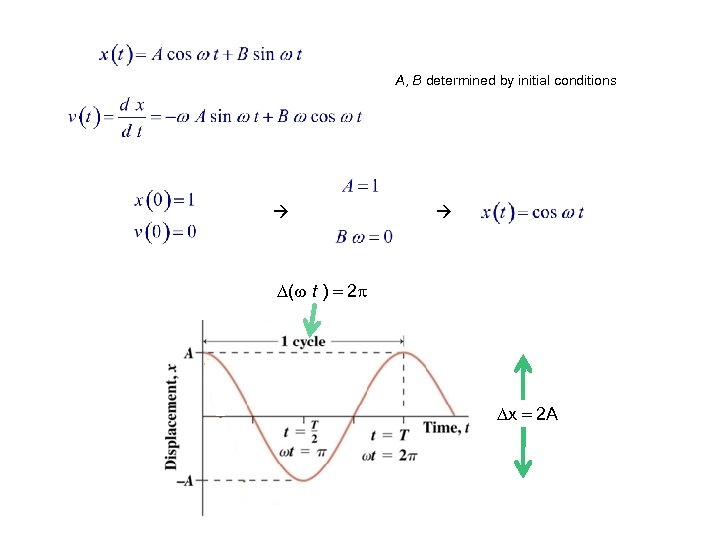 A, B determined by initial conditions ( t ) 2 x 2 A
A, B determined by initial conditions ( t ) 2 x 2 A
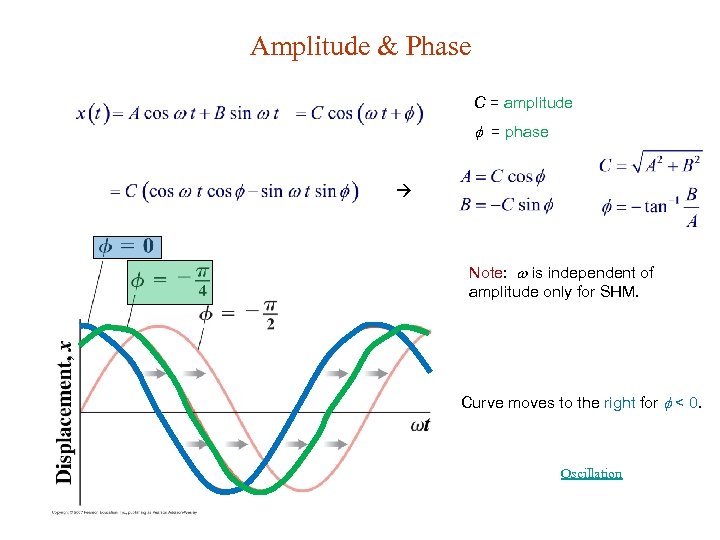 Amplitude & Phase C = amplitude = phase Note: is independent of amplitude only for SHM. Curve moves to the right for < 0. Oscillation
Amplitude & Phase C = amplitude = phase Note: is independent of amplitude only for SHM. Curve moves to the right for < 0. Oscillation
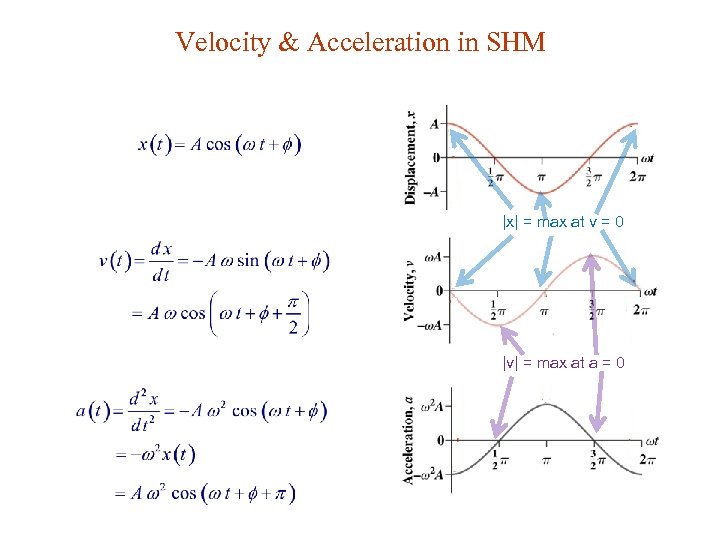 Velocity & Acceleration in SHM |x| = max at v = 0 |v| = max at a = 0
Velocity & Acceleration in SHM |x| = max at v = 0 |v| = max at a = 0
 GOT IT? 13. 1. Two identical mass-springs are displaced different amounts from equilibrium & then released at different times. Of the amplitudes, frequencies, periods, & phases of the subsequent motions, which are the same for both systems & which are different? Same: frequencies, periods Different: amplitudes ( different displacement ) phases ( different release time )
GOT IT? 13. 1. Two identical mass-springs are displaced different amounts from equilibrium & then released at different times. Of the amplitudes, frequencies, periods, & phases of the subsequent motions, which are the same for both systems & which are different? Same: frequencies, periods Different: amplitudes ( different displacement ) phases ( different release time )
 Application: Swaying skyscraper Tuned mass damper : Damper highly damped , Overall oscillation overdamped. Taipei 101 TMD: 41 steel plates, 730 ton, d = 550 cm, 87 th-92 nd floor. Also used in: Movie Tuned Mass Damper • Tall smokestacks • Airport control towers. • Power-plant cooling towers. • Bridges. • Ski lifts.
Application: Swaying skyscraper Tuned mass damper : Damper highly damped , Overall oscillation overdamped. Taipei 101 TMD: 41 steel plates, 730 ton, d = 550 cm, 87 th-92 nd floor. Also used in: Movie Tuned Mass Damper • Tall smokestacks • Airport control towers. • Power-plant cooling towers. • Bridges. • Ski lifts.
 Example 13. 2. Tuned Mass Damper The tuned mass damper in NY’s Citicorp Tower consists of a 373 -Mg (vs 101’s 3500 Mg) concrete block that completes one cycle of oscillation in 6. 80 s. The oscillation amplitude in a high wind is 110 cm. Determine the spring constant & the maximum speed & acceleration of the block.
Example 13. 2. Tuned Mass Damper The tuned mass damper in NY’s Citicorp Tower consists of a 373 -Mg (vs 101’s 3500 Mg) concrete block that completes one cycle of oscillation in 6. 80 s. The oscillation amplitude in a high wind is 110 cm. Determine the spring constant & the maximum speed & acceleration of the block.
 13. 3. Applications of Simple Harmonic Motion • The Vertical Mass-Spring System • The Torsional Oscillator • The Pendulum • The Physical Pendulum
13. 3. Applications of Simple Harmonic Motion • The Vertical Mass-Spring System • The Torsional Oscillator • The Pendulum • The Physical Pendulum
 The Vertical Mass-Spring System Spring stretched by x 1 when loaded. mass m oscillates about the new equil. pos. with freq
The Vertical Mass-Spring System Spring stretched by x 1 when loaded. mass m oscillates about the new equil. pos. with freq
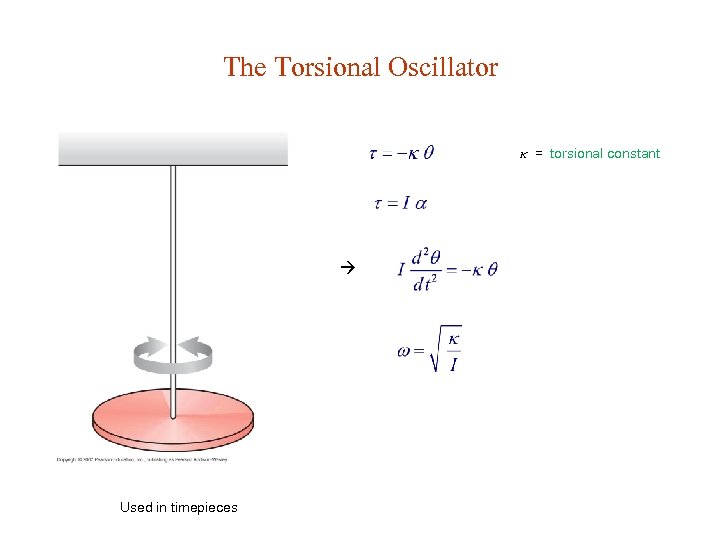 The Torsional Oscillator = torsional constant Used in timepieces
The Torsional Oscillator = torsional constant Used in timepieces
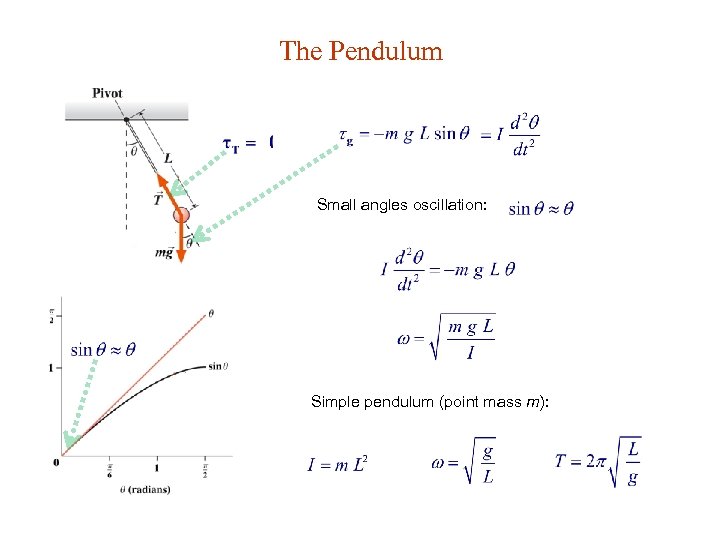 The Pendulum Small angles oscillation: Simple pendulum (point mass m):
The Pendulum Small angles oscillation: Simple pendulum (point mass m):
 Example 13. 3. Rescuing Tarzan stands on a branch as a leopard threatens. Jane is on a nearby branch of the same height, holding a 25 -m-long vine attached to a point midway between her & Tarzan. She grasps the vine & steps off with negligible velocity. How soon can she reach Tarzan? Time needed:
Example 13. 3. Rescuing Tarzan stands on a branch as a leopard threatens. Jane is on a nearby branch of the same height, holding a 25 -m-long vine attached to a point midway between her & Tarzan. She grasps the vine & steps off with negligible velocity. How soon can she reach Tarzan? Time needed:
 GOT IT? 13. 2. What happens to the period of a pendulum if no change (a) its mass is doubled, doubles (b) it’s moved to a planet whose g is ¼ that of Earth, doubles (c) its length is quadrupled?
GOT IT? 13. 2. What happens to the period of a pendulum if no change (a) its mass is doubled, doubles (b) it’s moved to a planet whose g is ¼ that of Earth, doubles (c) its length is quadrupled?
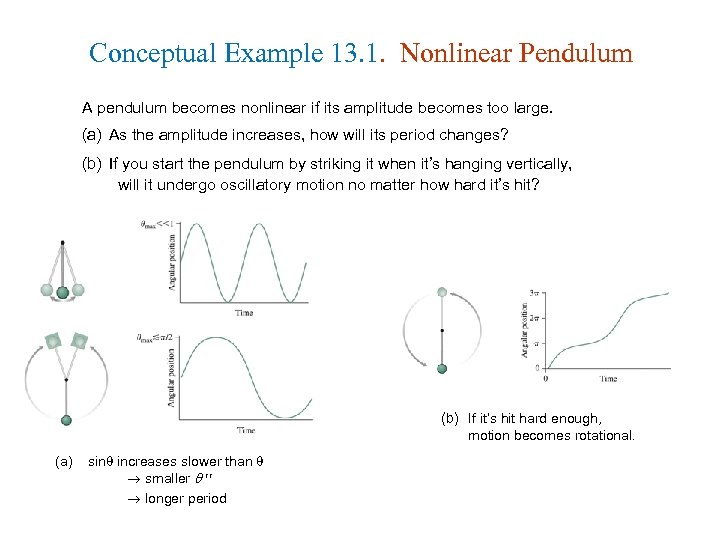 Conceptual Example 13. 1. Nonlinear Pendulum A pendulum becomes nonlinear if its amplitude becomes too large. (a) As the amplitude increases, how will its period changes? (b) If you start the pendulum by striking it when it’s hanging vertically, will it undergo oscillatory motion no matter how hard it’s hit? (b) If it’s hit hard enough, motion becomes rotational. (a) sin increases slower than smaller longer period
Conceptual Example 13. 1. Nonlinear Pendulum A pendulum becomes nonlinear if its amplitude becomes too large. (a) As the amplitude increases, how will its period changes? (b) If you start the pendulum by striking it when it’s hanging vertically, will it undergo oscillatory motion no matter how hard it’s hit? (b) If it’s hit hard enough, motion becomes rotational. (a) sin increases slower than smaller longer period
 The Physical Pendulum = any object that’s free to swing Small angular displacement SHM
The Physical Pendulum = any object that’s free to swing Small angular displacement SHM
 Example 13. 4. Walking When walking, the leg not in contact of the ground swings forward, acting like a physical pendulum. Approximating the leg as a uniform rod, find the period for a leg 90 cm long. Table 10. 2 Forward stride = T/2 = 0. 8 s
Example 13. 4. Walking When walking, the leg not in contact of the ground swings forward, acting like a physical pendulum. Approximating the leg as a uniform rod, find the period for a leg 90 cm long. Table 10. 2 Forward stride = T/2 = 0. 8 s
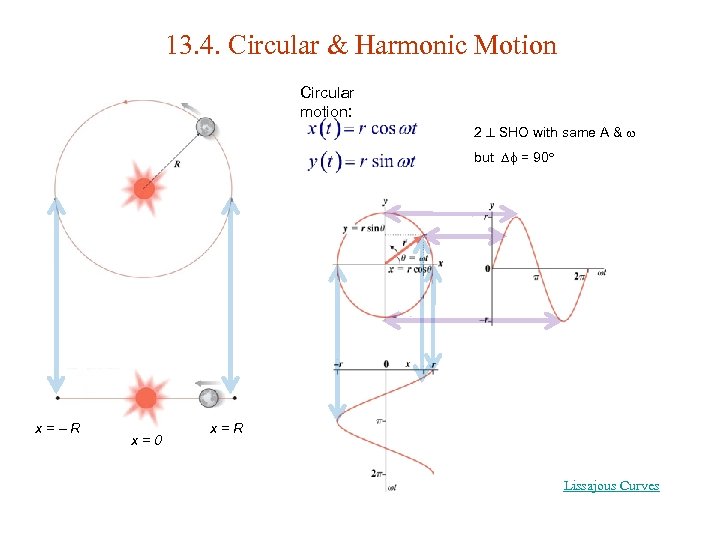 13. 4. Circular & Harmonic Motion Circular motion: 2 SHO with same A & but = 90 x= R x=0 x=R Lissajous Curves
13. 4. Circular & Harmonic Motion Circular motion: 2 SHO with same A & but = 90 x= R x=0 x=R Lissajous Curves
 GOT IT? 13. 3. The figure shows paths traced out by two pendulums swinging with different frequencies in the x- & y- directions. What are the ratios x : y ? 1: 2 3: 2 Lissajous Curves
GOT IT? 13. 3. The figure shows paths traced out by two pendulums swinging with different frequencies in the x- & y- directions. What are the ratios x : y ? 1: 2 3: 2 Lissajous Curves
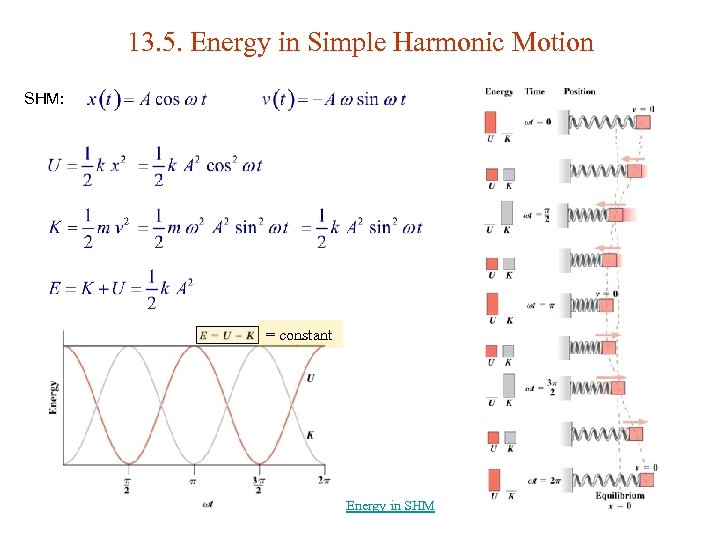 13. 5. Energy in Simple Harmonic Motion SHM: = constant Energy in SHM
13. 5. Energy in Simple Harmonic Motion SHM: = constant Energy in SHM
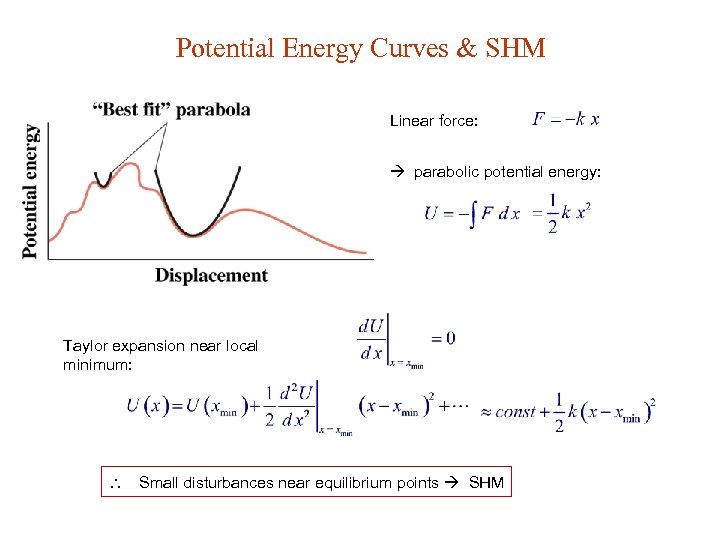 Potential Energy Curves & SHM Linear force: parabolic potential energy: Taylor expansion near local minimum: Small disturbances near equilibrium points SHM
Potential Energy Curves & SHM Linear force: parabolic potential energy: Taylor expansion near local minimum: Small disturbances near equilibrium points SHM
 GOT IT? 13. 4. Two different mass-springs oscillate with the same amplitude & frequency. If one has twice as much energy as the other, how do (a) their masses & (b) their spring constants compare? (c) What about their maximum speeds? The more energetic oscillator has (a) twice the mass (b) twice the spring constant (c) Their maximum speeds are equal.
GOT IT? 13. 4. Two different mass-springs oscillate with the same amplitude & frequency. If one has twice as much energy as the other, how do (a) their masses & (b) their spring constants compare? (c) What about their maximum speeds? The more energetic oscillator has (a) twice the mass (b) twice the spring constant (c) Their maximum speeds are equal.
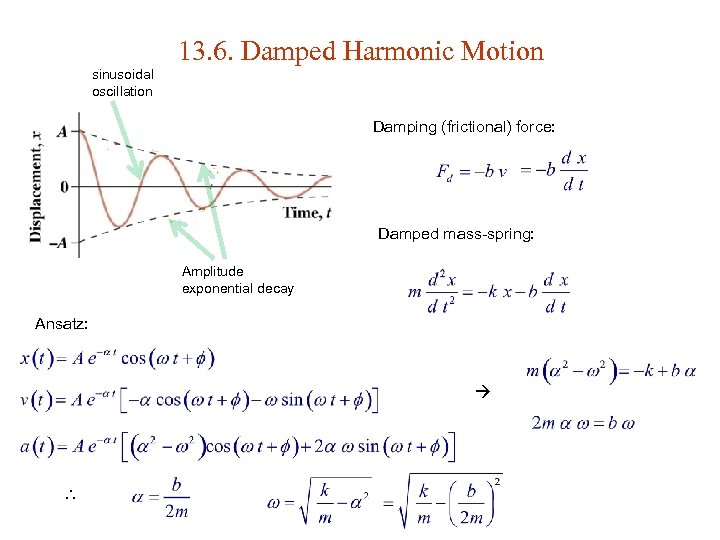 13. 6. Damped Harmonic Motion sinusoidal oscillation Damping (frictional) force: Damped mass-spring: Amplitude exponential decay Ansatz:
13. 6. Damped Harmonic Motion sinusoidal oscillation Damping (frictional) force: Damped mass-spring: Amplitude exponential decay Ansatz:
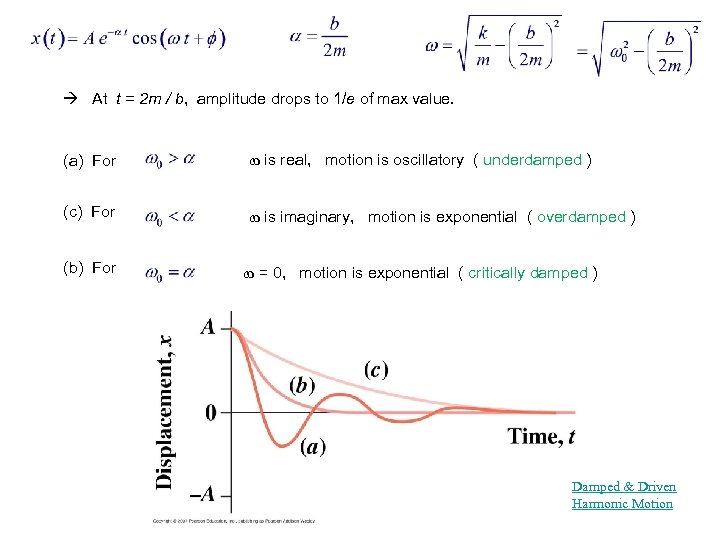 At t = 2 m / b, amplitude drops to 1/e of max value. (a) For is real, motion is oscillatory ( underdamped ) (c) For is imaginary, motion is exponential ( overdamped ) (b) For = 0, motion is exponential ( critically damped ) Damped & Driven Harmonic Motion
At t = 2 m / b, amplitude drops to 1/e of max value. (a) For is real, motion is oscillatory ( underdamped ) (c) For is imaginary, motion is exponential ( overdamped ) (b) For = 0, motion is exponential ( critically damped ) Damped & Driven Harmonic Motion
 Example 13. 6. Bad Shocks A car’s suspension has m = 1200 kg & k = 58 k. N / m. Its worn-out shock absorbers provide a damping constant b = 230 kg / s. After the car hit a pothole, how many oscillations will it make before the amplitude drops to half its initial value? Time required is # of oscillations: bad shock !
Example 13. 6. Bad Shocks A car’s suspension has m = 1200 kg & k = 58 k. N / m. Its worn-out shock absorbers provide a damping constant b = 230 kg / s. After the car hit a pothole, how many oscillations will it make before the amplitude drops to half its initial value? Time required is # of oscillations: bad shock !
 13. 7. Driven Oscillations & Resonance External force Driven oscillator Let d = driving frequency ( long time ) Prob 75: = natural frequency Resonance: Damped & Driven Harmonic Motion
13. 7. Driven Oscillations & Resonance External force Driven oscillator Let d = driving frequency ( long time ) Prob 75: = natural frequency Resonance: Damped & Driven Harmonic Motion
 Buildings, bridges, etc have natural freq. If Earth quake, wind, etc sets up resonance, disasters result. Collapse of Tacoma bridge is due to self-excitation described by the van der Pol equation. Tacoma Bridge Resonance in microscopic system: • electrons in magnetron microwave oven • Tokamak (toroidal magnetic field) fusion • CO 2 vibration: resonance at IR freq Green house effect • Nuclear magnetic resonance (NMR) NMI for medical use.
Buildings, bridges, etc have natural freq. If Earth quake, wind, etc sets up resonance, disasters result. Collapse of Tacoma bridge is due to self-excitation described by the van der Pol equation. Tacoma Bridge Resonance in microscopic system: • electrons in magnetron microwave oven • Tokamak (toroidal magnetic field) fusion • CO 2 vibration: resonance at IR freq Green house effect • Nuclear magnetic resonance (NMR) NMI for medical use.


