Part of MATERIALS SCIENCE A Learner s Guide

Part of MATERIALS SCIENCE & A Learner’s Guide ENGINEERING AN INTRODUCTORY E-BOOK Anandh Subramaniam & Kantesh Balani Materials Science and Engineering (MSE) Indian Institute of Technology, Kanpur- 208016 Email: anandh@iitk. ac. in, URL: home. iitk. ac. in/~anandh http: //home. iitk. ac. in/~anandh/E-book. htm Interested readers may refer to this excellent article “Space Subdivision and Voids Inside Body-Centred Cubic Lattices” Claudio Giomini and Giancarlo Marrosu Chem. Educator 16 (2011) 232– 237.

Interatomic Voids* q When an atom of an alloying element/impurity is added to a pure crystal, the atom added may ‘sit’ in a lattice/sublattice site in place of the host atom (e. g. Ag added to Au sits in a FCC lattice site→ Ag is a substitutional alloying element) or ‘go into’ the space between atoms (e. g. C added to Fe→ C is a interstitial alloying element). In some rare cases the atoms may be present both in the lattice and interstitial sites (e. g. B in steel). q If the ‘fit’ of the added atom in the ‘available space’ is not too bad, then the solubility of the added element in the host crystal is expected to be good. q In the hard sphere model of atoms, atoms are visualized as spheres. We have already seen that as spheres cannot fill entire space. This implies that the packing fraction (PF) < 1 (for all crystals). q This further implies there is void space between the atoms. Lower the PF, larger the volume occupied by the void space. q We are mostly interested in the largest sphere which can fit into these voids. q The void space forms a continuous network across the whole solid. Part of this void space lies within the unit cell (which when translated by the lattice translation vectors gives rise to the entire void space). * Do not confuse these voids with microscopic/macroscopic voids/cracks in crystals or holes (semiconductors) or vacancies (missing atoms). Note: in some cases the void within a crystal can be large enough to accommodate small/large molecules (e. g. in Metal Organic Frameworks) → we are not going to describe these voids in this set of slides.

q This void space within the unit cell has a complicated shape, but (typically) we only consider the plane faced polyhedron version of the voids. q There may be more than one type of such void polyhedra in a single unit cell. These void polyhedra when put together fill space; however, in some cases only a part of a given polyhedron may lie within a unit cell. q The size and distribution of voids* in materials plays a role in determining aspects of material behaviour e. g. solubility of interstitials and their diffusivity. q The position of the voids of a particular type will be consistent with the symmetry of the crystal (if a void of a particular type is located at (x, y, z), then all similar voids can be obtained by the symmetry operations of the crystal). q In the close packed crystals (FCC, HCP) there are two types of voids tetrahedral and octahedral voids (identical in both the structures as the voids are formed between two layers of atoms) q The octahedral void has a coordination number 6 (should not be confused with 8 coordination!) q In the ‘BCC crystal’ the voids do NOT have the shape of the regular tetrahedron or the regular octahedron (in fact the octahedral void is a ‘linear void’!!) * Common way of referring to the void polyhedron/polyhedra.

SC q The simple cubic crystal (monoatomic decoration of the simple cubic lattice) has large void in the centre of the unit cell with a coordination number of 8. q The actual space of the void in very complicated (right hand figure below) and the polyhedron version of the void is the cube (as cube is the coordination polyhedron around a atom sitting in the void). q Voids in SC crystal are not often described in detail in text books as the only element crystallizing SC structure is Polonium. True Unit Cell of SC crystal Polyhedral model (Cube) Video: void in SC crystal Actual shape of the void (space)! § Later on we will talk about tetrahedral and octahedral voids in FCC, BCC & HCP crystals: note that there are NO such tetrahedral and octahedral voids in SC crystals and the only polyhedral void is CUBIC (i. e. coordination number of 8).

CCP q Actual shape of the void is as shown below. This shape is very complicated and we use the polyhedral version of the void. The polyhedra involved are the regular tetrahedron and the regular octahedron (referred to as the tetrahedral and octahedral voids). Actual shape of the void Ignore the nonidealities in the wax casting process! Position of some of the atoms w. r. t to the void

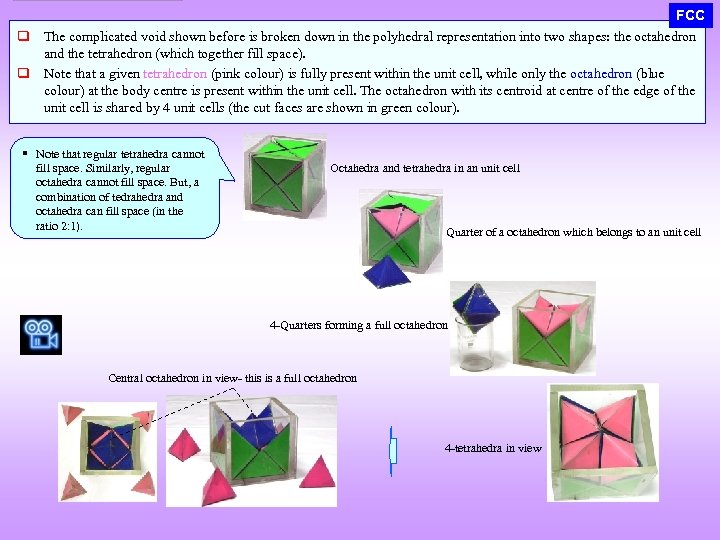q q FCC The complicated void shown before is broken down in the polyhedral representation into two shapes: the octahedron and the tetrahedron (which together fill space). Note that a given tetrahedron (pink colour) is fully present within the unit cell, while only the octahedron (blue colour) at the body centre is present within the unit cell. The octahedron with its centroid at centre of the edge of the unit cell is shared by 4 unit cells (the cut faces are shown in green colour). § Note that regular tetrahedra cannot fill space. Similarly, regular octahedra cannot fill space. But, a combination of tedrahedra and octahedra can fill space (in the ratio 2: 1). Octahedra and tetrahedra in an unit cell Quarter of a octahedron which belongs to an unit cell 4 -Quarters forming a full octahedron Central octahedron in view- this is a full octahedron 4 -tetrahedra in view

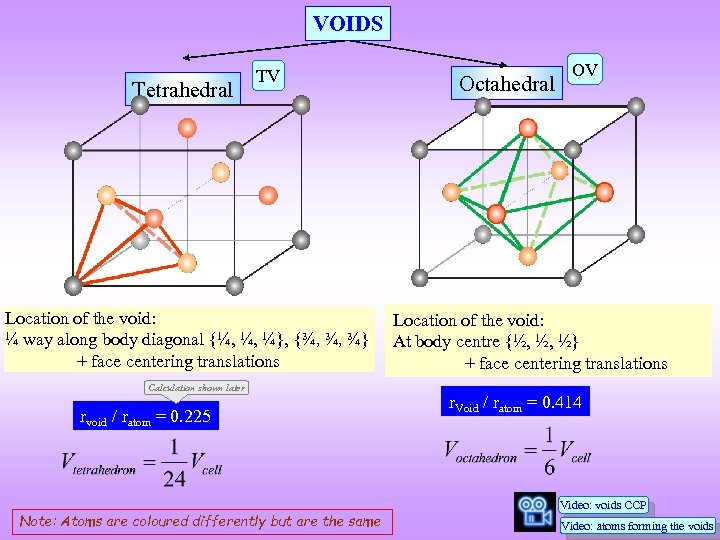VOIDS Tetrahedral TV Location of the void: ¼ way along body diagonal {¼, ¼, ¼}, {¾, ¾, ¾} + face centering translations Calculation shown later rvoid / ratom = 0. 225 Note: Atoms are coloured differently but are the same Octahedral OV Location of the void: At body centre {½, ½, ½} + face centering translations r. Void / ratom = 0. 414 Video: voids CCP Video: atoms forming the voids

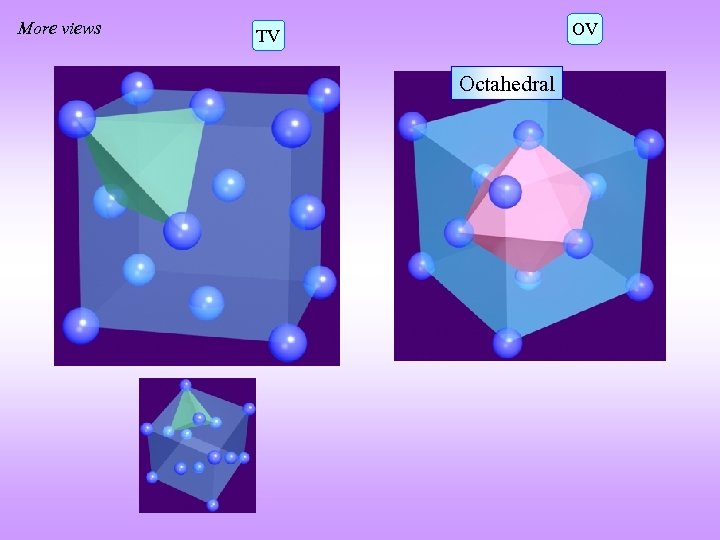More views OV TV Tetrahedral Octahedral

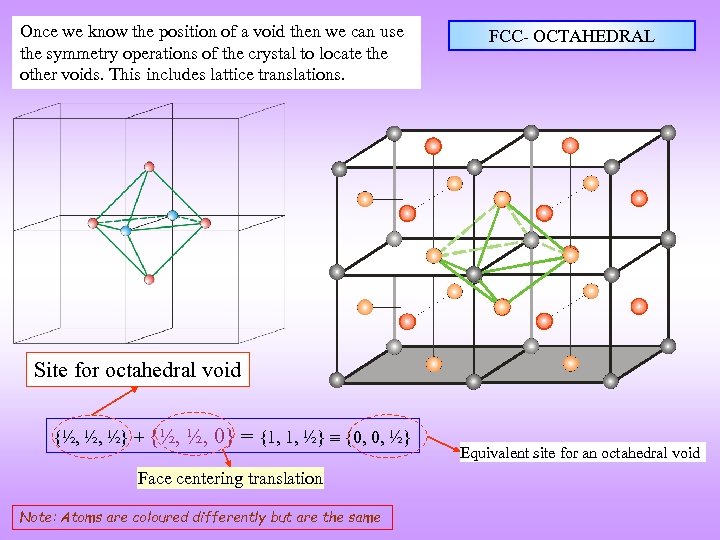Once we know the position of a void then we can use the symmetry operations of the crystal to locate the other voids. This includes lattice translations. FCC- OCTAHEDRAL Site for octahedral void {½, ½, ½} + {½, ½, 0} = {1, 1, ½} {0, 0, ½} Face centering translation Note: Atoms are coloured differently but are the same Equivalent site for an octahedral void

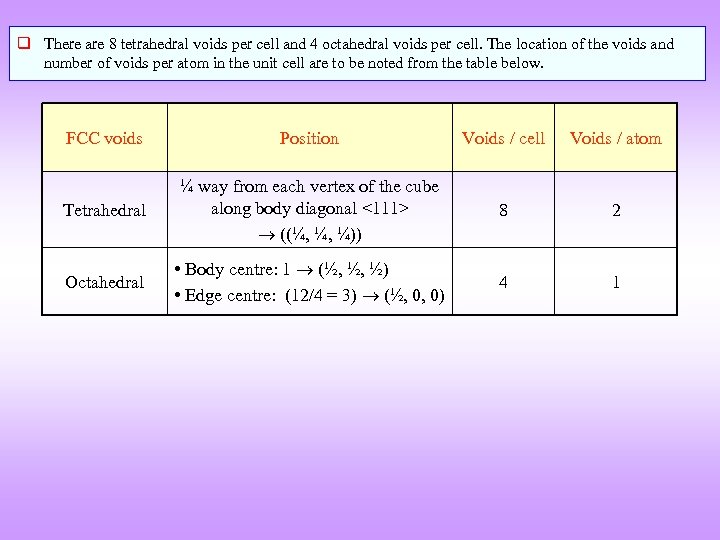q There are 8 tetrahedral voids per cell and 4 octahedral voids per cell. The location of the voids and number of voids per atom in the unit cell are to be noted from the table below. FCC voids Position Voids / cell Voids / atom Tetrahedral ¼ way from each vertex of the cube along body diagonal <111> ((¼, ¼, ¼)) 8 2 Octahedral • Body centre: 1 (½, ½, ½) • Edge centre: (12/4 = 3) (½, 0, 0) 4 1

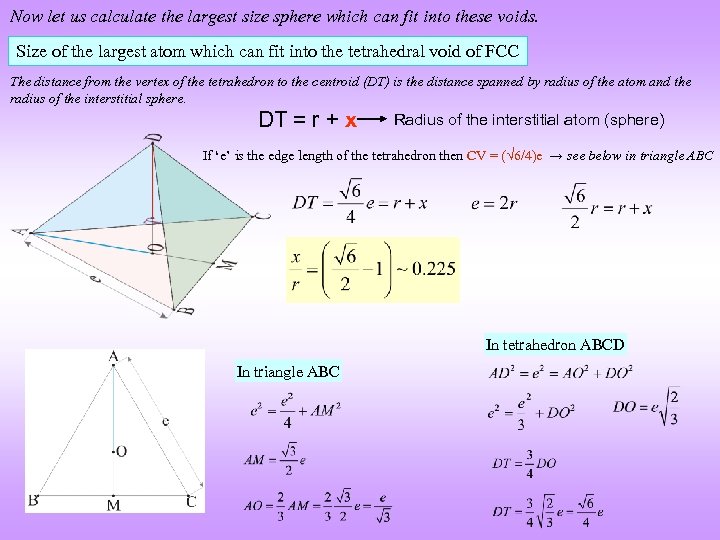Now let us calculate the largest size sphere which can fit into these voids. Size of the largest atom which can fit into the tetrahedral void of FCC The distance from the vertex of the tetrahedron to the centroid (DT) is the distance spanned by radius of the atom and the radius of the interstitial sphere. DT = r + x Radius of the interstitial atom (sphere) If ‘e’ is the edge length of the tetrahedron then CV = ( 6/4)e → see below in triangle ABC In tetrahedron ABCD In triangle ABC

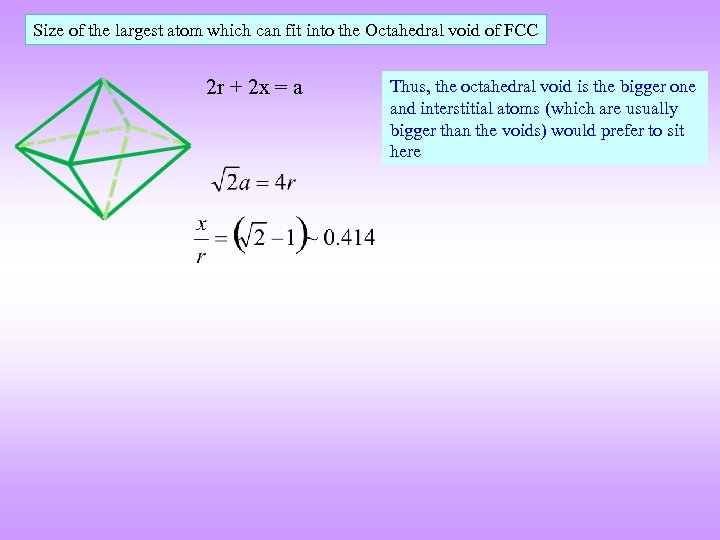Size of the largest atom which can fit into the Octahedral void of FCC 2 r + 2 x = a Thus, the octahedral void is the bigger one and interstitial atoms (which are usually bigger than the voids) would prefer to sit here

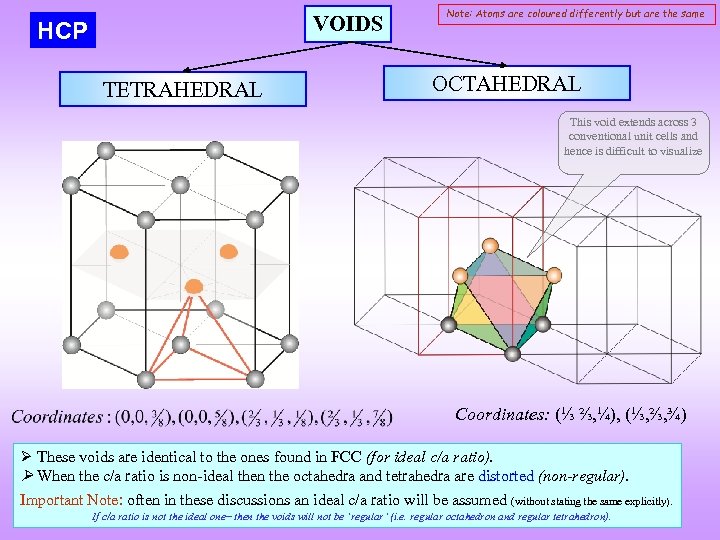VOIDS HCP TETRAHEDRAL Note: Atoms are coloured differently but are the same OCTAHEDRAL This void extends across 3 conventional unit cells and hence is difficult to visualize Coordinates: (⅓ ⅔, ¼), (⅓, ⅔, ¾) These voids are identical to the ones found in FCC (for ideal c/a ratio). When the c/a ratio is non-ideal then the octahedra and tetrahedra are distorted (non-regular). Important Note: often in these discussions an ideal c/a ratio will be assumed (without stating the same explicitly). If c/a ratio is not the ideal one then the voids will not be ‘regular’ (i. e. regular octahedron and regular tetrahedron).

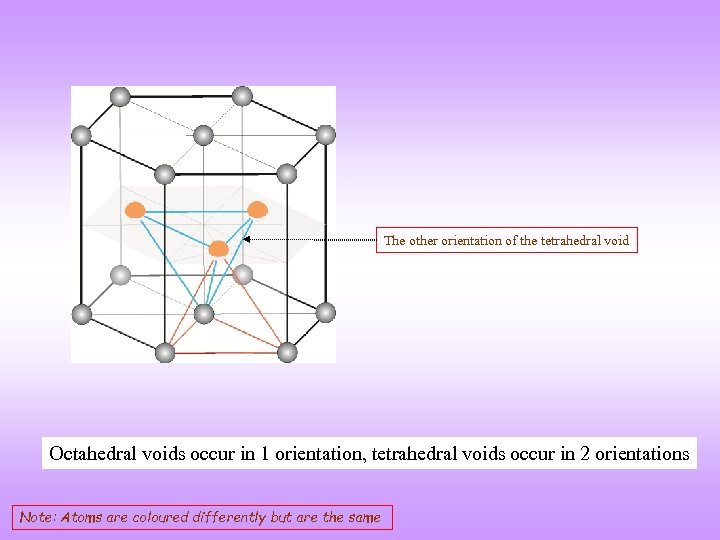The other orientation of the tetrahedral void Octahedral voids occur in 1 orientation, tetrahedral voids occur in 2 orientations Note: Atoms are coloured differently but are the same

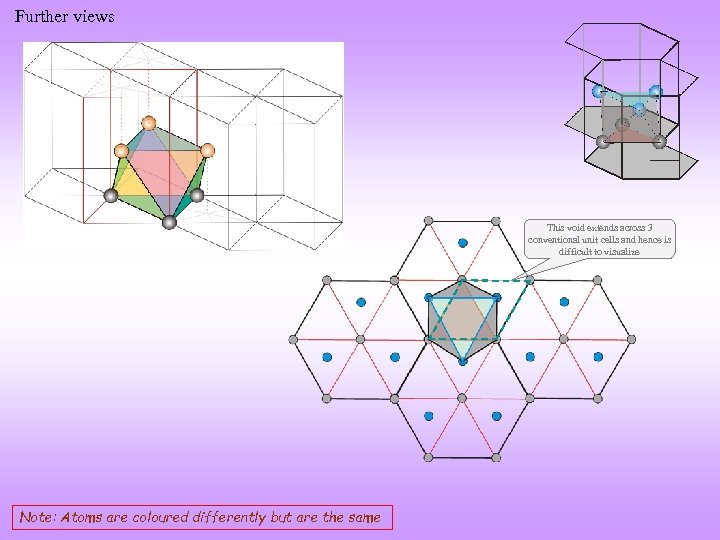Further views This void extends across 3 conventional unit cells and hence is difficult to visualize Note: Atoms are coloured differently but are the same

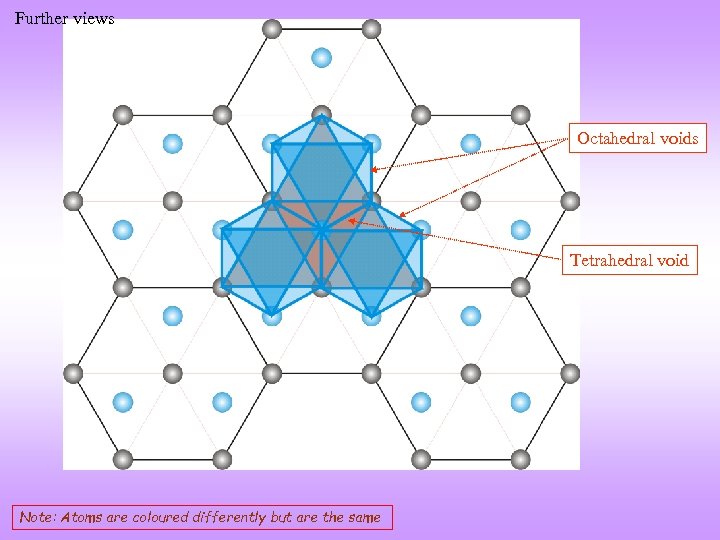Further views Octahedral voids Tetrahedral void Note: Atoms are coloured differently but are the same

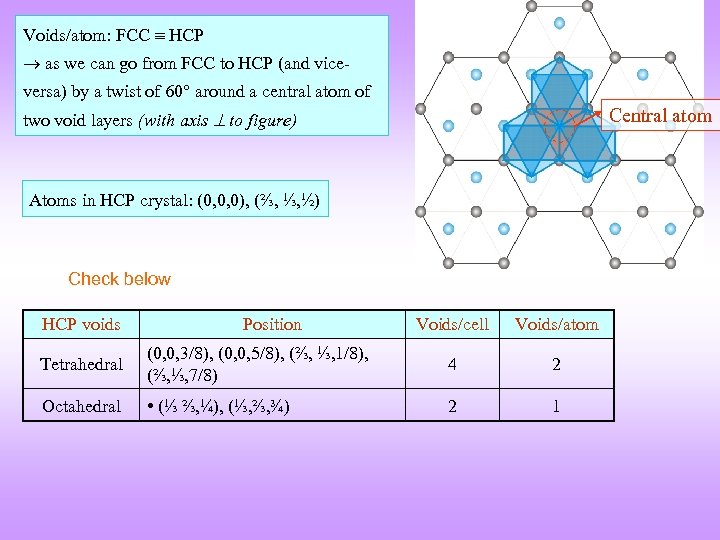Voids/atom: FCC HCP as we can go from FCC to HCP (and viceversa) by a twist of 60 around a central atom of Central atom two void layers (with axis to figure) Atoms in HCP crystal: (0, 0, 0), (⅔, ⅓, ½) Check below HCP voids Position Voids/cell Voids/atom Tetrahedral (0, 0, 3/8), (0, 0, 5/8), (⅔, ⅓, 1/8), (⅔, ⅓, 7/8) 4 2 Octahedral • (⅓ ⅔, ¼), (⅓, ⅔, ¾) 2 1

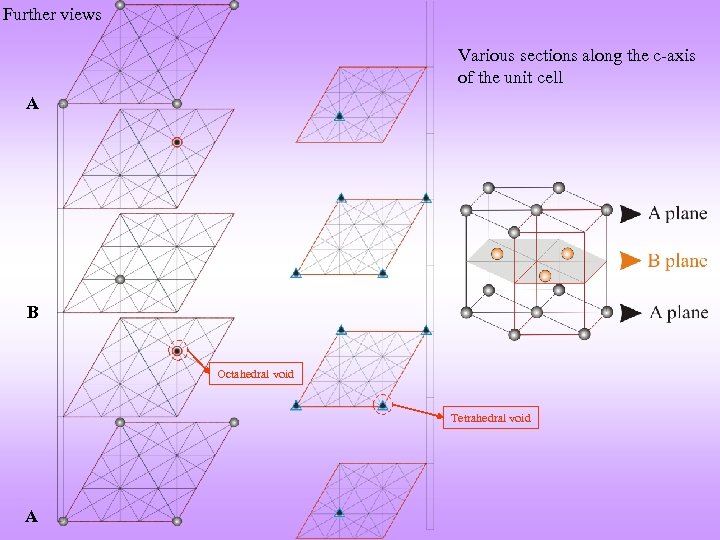Further views Various sections along the c-axis of the unit cell A B Octahedral void Tetrahedral void A

Further views with some models Visualizing these voids can sometimes be difficult especially in the HCP crystal. ‘How the tetrahedral and octahedral void fill space? ’ is shown in the accompanying video Video: Polyhedral voids filling space

Voids in BCC crystal q Let us start with some surprising facts (which we shall list later as well): (i) In a CCP crystal the octahedral void can host a bigger sphere than the tetrahedral void– the reverse is true in BCC crystals. (ii) In the case of Fe the solubility of C in close packed CCP structure is more than the non-close packed BCC structure. (ii) In BCC Fe, C sits in the octahedral void (which can host a smaller sphere) in preference to the tetrahedral void (which can host a larger sphere). q The solubility of C in Fe (both FCC & BCC) is much lower than the available interstitial void space. q There are NO voids in a ‘BCC crystal’ which have the shape of a regular polyhedron (one of the 5 Platonic solids) q The voids in BCC crystal are: distorted ‘octahedral’ and distorted tetrahedral → the correct term should be non-regular instead of distorted (the ‘distortions’ are ‘pretty regular’ as we shall see shortly). q The distorted octahedral void is in a sense a ‘linear void’! an sphere of correct size sitting in the void touches only two of the six atoms surrounding it q Carbon prefers to sit in this smaller ‘octahedral void’ for reasons which we shall see soon.

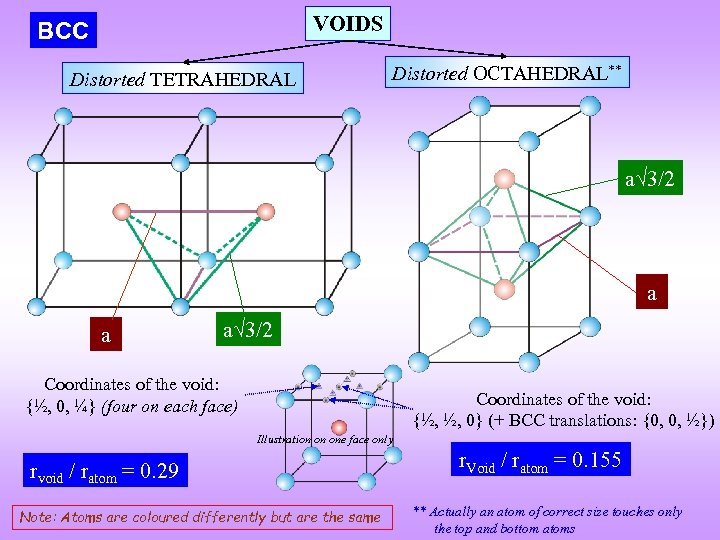VOIDS BCC Distorted TETRAHEDRAL Distorted OCTAHEDRAL** a 3/2 a a a 3/2 Coordinates of the void: {½, 0, ¼} (four on each face) Coordinates of the void: {½, ½, 0} (+ BCC translations: {0, 0, ½}) Illustration on one face only rvoid / ratom = 0. 29 Note: Atoms are coloured differently but are the same r. Void / ratom = 0. 155 ** Actually an atom of correct size touches only the top and bottom atoms

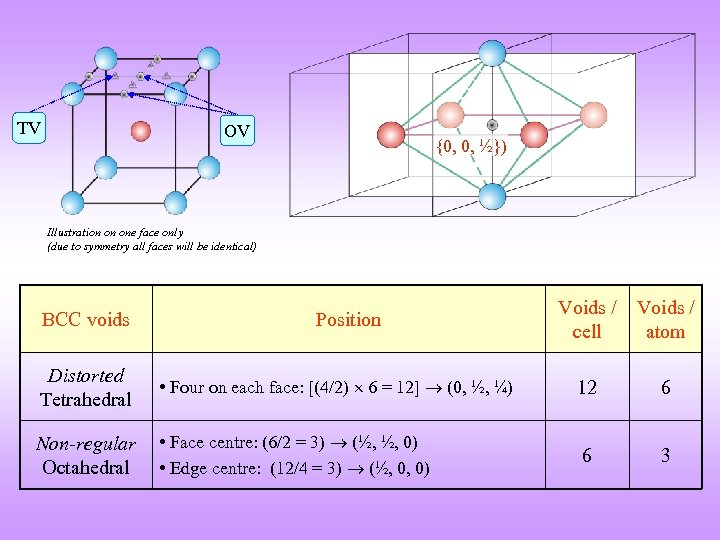TV OV {0, 0, ½}) Illustration on one face only (due to symmetry all faces will be identical) BCC voids Position Voids / cell Voids / atom Distorted Tetrahedral • Four on each face: [(4/2) 6 = 12] (0, ½, ¼) 12 6 Non-regular Octahedral • Face centre: (6/2 = 3) (½, ½, 0) • Edge centre: (12/4 = 3) (½, 0, 0) 6 3

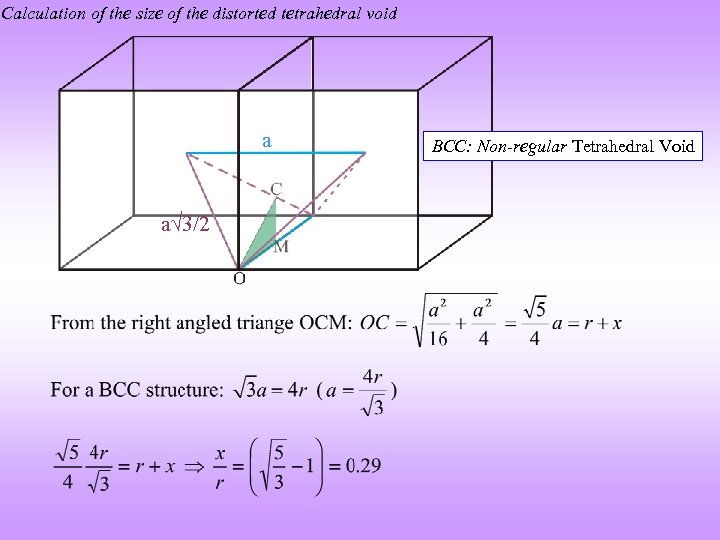Calculation of the size of the distorted tetrahedral void a a 3/2 BCC: Non-regular Tetrahedral Void

Calculation of the size of the distorted octahedral void Non-regular Octahedral Void As the distance OA > OB the atom in the void touches only the atom at B (body centre). void is actually a ‘linear’ void* a 3/2 a * Point regarding ‘Linear Void’ § Because of this aspect the OV along the 3 axes can be differentiated into OVx, OVy & OVz § Similarly the TV along x, y, z can be differentiated This implies:

Where does the carbon atom sit in the BCC and FCC forms of iron? How does it affect the solubility of carbon in these forms of Fe? Surprising facts! q C dissolves more in the close packed structure (FCC, -Fe) (albeit at higher temperatures at 1 atm. pressure where FCC is stable) than in the open structure (BCC-Fe). q Solubility CCP Fe 2. 06 wt. % at 1147ºC, BCC Fe 0. 008 wt. % at RT & 0. 025% at 723 C. q C sits in the smaller octahedral void in BCC in preference to the larger tetrahedral void. q Fe carbon alloys are important materials and hence we consider them next. q The octahedral void in FCC is the larger one and less distortion occurs when carbon sits there this aspect contributes to a higher solubility of C in -Fe. q The distorted (non-regular) octahedral void in BCC is the smaller one but (surprisingly) carbon sits there in preference to the distorted tetrahedral void (the bigger one) - (we shall see the reason shortly). q Due to small size of the voids in BCC the distortion caused is more and the solubility of C in -Fe is small this is rather surprising at a first glance as BCC is the more open structure but we have already seen that the number of voids in BCC is more than that in FCC i. e. BCC has more number of smaller voids. See next slide for figures

Spend some time over this slide FCC Relative size of voids, interstitials and Fe atom Void (Oct) Void (Tet) Size of Fe atom CCP crystal Fe. CCP C N Size of the OV H Size of Carbon atom Relative sizes of voids w. r. t to atoms Note the difference in size of the atoms BCC Size of Fe atom BCC crystal Size of the TV Fe. BCC Size of the OV

§ We had mentioned that the octahedral void in BCC is a linear one (interstitial atom actually touches only two out of the 6 atoms surrounding it). § In the next slide we make a approximate calculation to see till what size will it continue to touch only two Fe atoms (these are ‘ideal’ simplified geometrical calculations and in reality other complications will have to be considered).

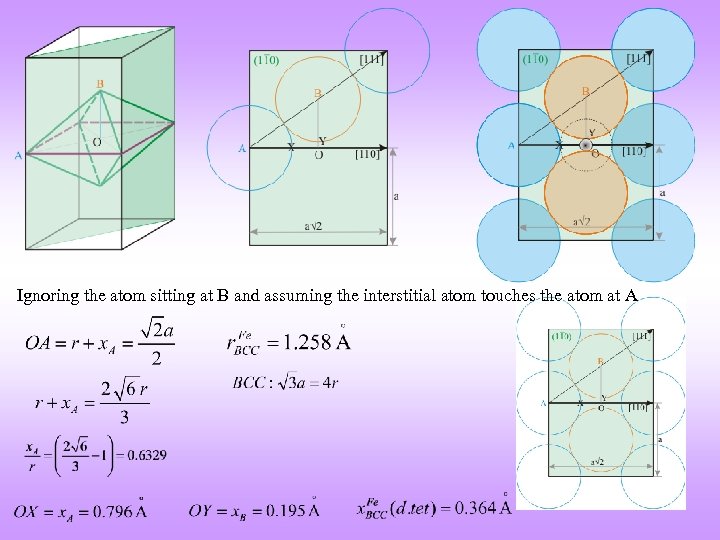Ignoring the atom sitting at B and assuming the interstitial atom touches the atom at A

§ This implies for x/r ratios between 0. 15 and 0. 63 the interstitial atom has to push only two atoms. § (xcarbon/r. Fe)BCC ~ 0. 6 § This explains why Carbon preferentially sits in the apparently smaller octahedral void in BCC.

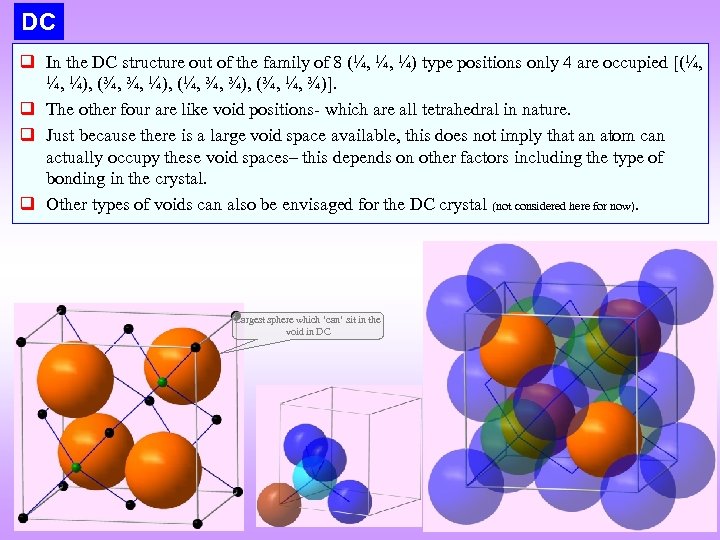DC q In the DC structure out of the family of 8 (¼, ¼, ¼) type positions only 4 are occupied [(¼, ¼, ¼), (¾, ¾, ¼), (¼, ¾, ¾), (¾, ¼, ¾)]. q The other four are like void positions- which are all tetrahedral in nature. q Just because there is a large void space available, this does not imply that an atom can actually occupy these void spaces– this depends on other factors including the type of bonding in the crystal. q Other types of voids can also be envisaged for the DC crystal (not considered here for now). Largest sphere which ‘can’ sit in the void in DC

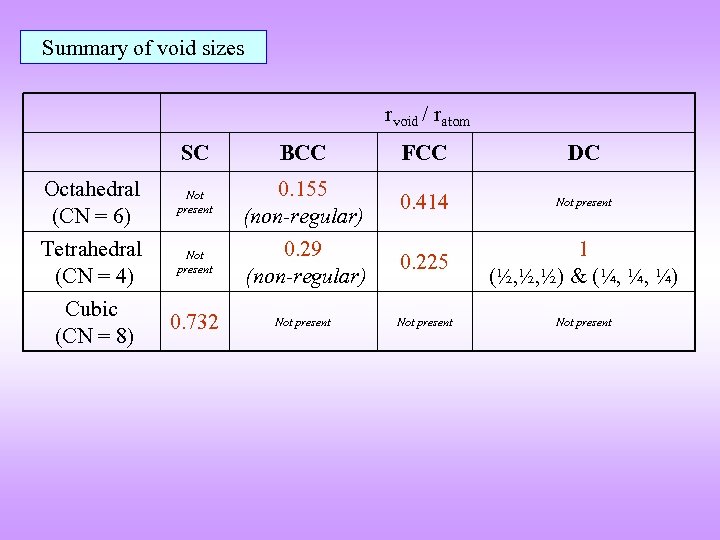Summary of void sizes rvoid / ratom SC BCC FCC DC Octahedral (CN = 6) Not present 0. 155 (non-regular) 0. 414 Not present Tetrahedral (CN = 4) Not present 0. 29 (non-regular) 0. 225 1 (½, ½, ½) & (¼, ¼, ¼) Cubic (CN = 8) 0. 732 Not present

Funda Check Some points and checks on voids! q Voids should not be confused with vacancies- vacancies are due to missing atoms or ions in crystals. q Holes should also not be confused with voids- holes are ‘missing electrons’ from the valence band of a solid. q In other contexts a ‘void’ could also imply a larger void* (of the size of nanometers or microns) and not the void between atoms in a crystal structure. q Voids have complicated shapes- we usually use a polyhedral version – the coordination polyhedron around a sphere of ‘correct size’. q Sometimes, as in the case of ‘octahedral void’ in the BCC- the second nearest neighbours are also included in constructing the coordination polyhedron. q In ionic crystals, unlike metallic crystals the cation ‘does not sit’ in the void formed by the anions- the cation is bigger than the anion. The void size calculation is to demarcate the regimes of various coordination structures. q If an interstitial atom wants to jump from one metastable equilibrium position to another- it has to cross an energy barrier. q Diffusivity of interstitial atoms (like C in Fe) is expected to be faster at a given temperature, as compared to substitutional atoms. This is because, typically most of the interstitial sites are vacant and hence an interstitial atom can jump from one site to neighbouring site. q The solubility of an interstitial element is often much smaller than the available void space. This is due to the overall strain energy cost of introducing an interstitial solute. * Schematic of a ‘large void’ implied under some circumstances