Part 3 Linear Programming 3 3 Theoretical Analysis

Part 3 Linear Programming 3. 3 Theoretical Analysis

Matrix Form of the Linear Programming Problem

LP Solution in Matrix Form

Tableau in Matrix Form

Criteria for Determining A Minimum Feasible Solution

Theorem (Improvement of Basic Feasible Solution) • Given a non-degenerate basic feasible solution with corresponding objective function f 0, suppose for some j there holds cj-fj<0. Then there is a feasible solution with objective value f

Optimality Condition If for some basic feasible solution cj-fj or rj is larger than or equal to zero for all j, then the solution is optimal.

Symmetric Form of Duality (1)

Symmetric Form of Duality (2) 1. MAX in primal; MIN in dual. 2. <= in constraints of primal; >= in constraints of dual. 3. Number of constraints in primal = Number of variable in dual 4. Number of variables in primal = Number of constraints in dual 5. Coefficients of x in objective function = RHS of constraints in dual 6. RHS of the constraints in primal = Coefficients of y in dual 7. f(xopt)=g(yopt)

Symmetric Form of Duality (3)

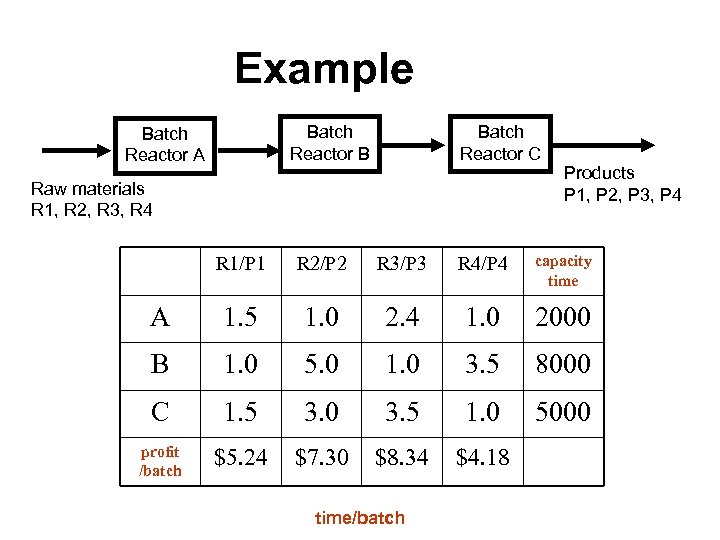Example Batch Reactor B Batch Reactor A Batch Reactor C Raw materials R 1, R 2, R 3, R 4 Products P 1, P 2, P 3, P 4 R 1/P 1 R 2/P 2 R 3/P 3 R 4/P 4 capacity time A 1. 5 1. 0 2. 4 1. 0 2000 B 1. 0 5. 0 1. 0 3. 5 8000 C 1. 5 3. 0 3. 5 1. 0 5000 profit /batch $5. 24 $7. 30 $8. 34 $4. 18 time/batch

Example: Primal Problem

Example: Dual Problem

Property 1 For any feasible solution to the primal problem and any feasible solution to the dual problem, the value of the primal objective function being maximized is always equal to or less than the value of the dual objective function being minimized.

Proof

Property 2

Proof

Duality Theorem If either the primal or dual problem has a finite optimal solution, so does the other, and the corresponding values of objective functions are equal. If either problem has an unbounded objective, the other problem has no feasible solution.

Additional Insights

Symmetric Form of Duality (3)

LP Solution in Matrix Form

Relations associated with the Optimal Feasible Solution of the Primal problem

Example PRIMAL DUAL

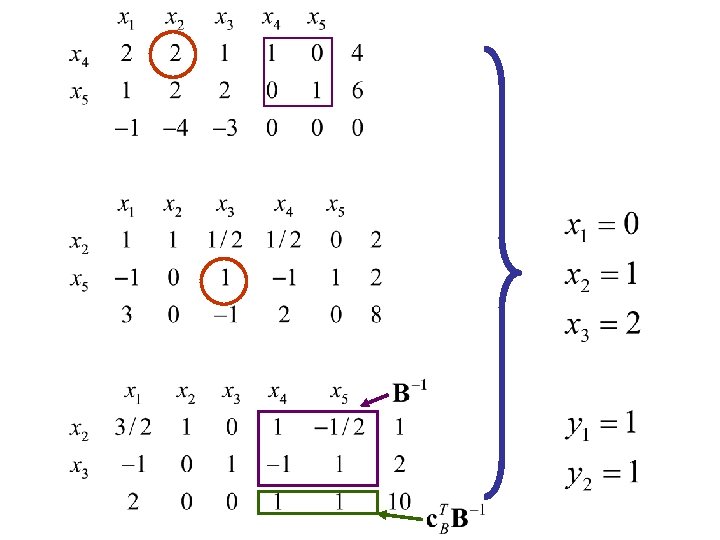
Tableau in Matrix Form

Example: The Primal Diet Problem How can we determine the most economical diet that satisfies the basic minimum nutritional requirements for good health? We assume that 1. There available at the market n different foods that the ith food sells at a price ci per unit. 2. There are m basic nutritional ingredients and, to achieve a balanced diet, each individual must receive at least bj unit of the jth nutrient per day. 3. Each unit of food i contains aji units of the jth nutrient.

Primal Formulation

The Dual Diet Problem Imagine a pharmaceutical company that produces in pill form each of the nutrients considered important by the dietician. The pharmaceutical company tries to convince the dietician to buy pills, and thereby supplies the nutrients directly rather than through purchase of various food. The problem faced by the drug company is that of determining positive unit prices y 1, y 2, …, ym for the nutrients so as to maximize the revenue while at the same time being competitive with real food. To be competitive with the real food, the cost a unit of food made synthetically from pure nutrients bought from the druggist must be no greater than ci, the market price of the food, i. e. y 1 a 1 i + y 2 a 2 i + … + ym ami <= ci.

Dual Formulation

Shadow Prices How does the minimum cost change if we change the right hand side b? If the changes are small, then the corner which was optimal remains optimal. The choice of basic variables does not change. At the end of simplex method, the corresponding m columns of A make up the basis matrix B.