 Part 2 Analysis of Variance 1
Part 2 Analysis of Variance 1
 СHAPTER QUESTIONS 1. Measures of Variability: Range, mean absolute deviation (MAD), Variance, Standard Deviation, Coefficient of Variation 2. Measures of dispersion for ungrouped data 3. Measures of dispersion for grouped data 4. Mean and variance of the alternative feature
СHAPTER QUESTIONS 1. Measures of Variability: Range, mean absolute deviation (MAD), Variance, Standard Deviation, Coefficient of Variation 2. Measures of dispersion for ungrouped data 3. Measures of dispersion for grouped data 4. Mean and variance of the alternative feature
 Variability and Measures of variability 1) (apple, . . . , apple) (in other words, all apples) 2) (apple, . . . , apple, pear) (apples and a pear), 3) (apple, pear, apple, . . . , pear) (a mixture of apples and pears). Of course, these examples can also be presented in the form of sets of numbers, as is usually done in textbooks on statistics: 1) (1, 1, . . . , 1), 2) (1, 1, . . . , 1, 0), 3) (1, 0, 0, 1, . . . , 0).
Variability and Measures of variability 1) (apple, . . . , apple) (in other words, all apples) 2) (apple, . . . , apple, pear) (apples and a pear), 3) (apple, pear, apple, . . . , pear) (a mixture of apples and pears). Of course, these examples can also be presented in the form of sets of numbers, as is usually done in textbooks on statistics: 1) (1, 1, . . . , 1), 2) (1, 1, . . . , 1, 0), 3) (1, 0, 0, 1, . . . , 0).
 • Range – The range of a set of measurements is the difference between the largest and smallest values in the data set. – Its major advantage is the ease with which it can be computed. – It is very sensitive to the smallest and largest data values – Its major shortcoming is its failure to provide information on the dispersion of the values between the two end points.
• Range – The range of a set of measurements is the difference between the largest and smallest values in the data set. – Its major advantage is the ease with which it can be computed. – It is very sensitive to the smallest and largest data values – Its major shortcoming is its failure to provide information on the dispersion of the values between the two end points.
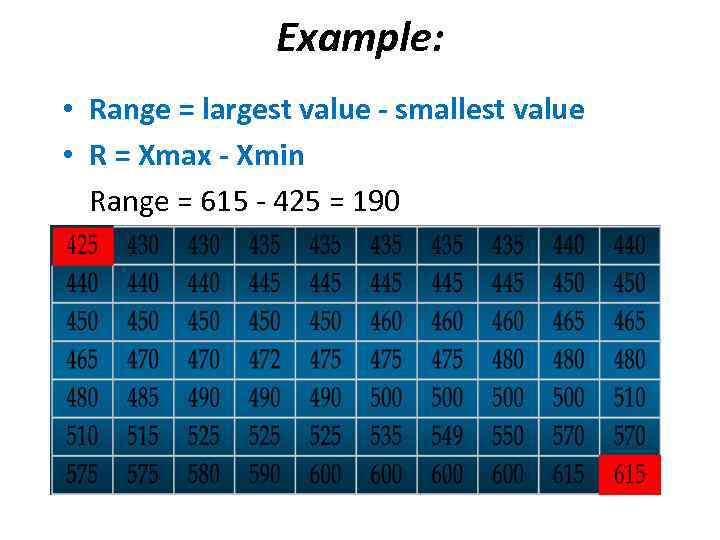 Example: • Range = largest value - smallest value • R = Xmax - Xmin Range = 615 - 425 = 190
Example: • Range = largest value - smallest value • R = Xmax - Xmin Range = 615 - 425 = 190
 Percentiles • A percentile provides information about how the data are spread over the interval from the smallest value to the largest value. • Admission test scores for colleges and universities are frequently reported in terms of percentiles.
Percentiles • A percentile provides information about how the data are spread over the interval from the smallest value to the largest value. • Admission test scores for colleges and universities are frequently reported in terms of percentiles.
 Percentiles • The pth percentile of a data set is a value such that at least p percent of the items take on this value or less and at least (100 - p) percent of the items take on this value or more. – Arrange the data in ascending order. – Compute index i, the position of the pth percentile. – i = (p/100)n – If i is not an integer, round up. The p th percentile is the value in the i th position. – If i is an integer, the p th percentile is the average of the values in positions i and i +1.
Percentiles • The pth percentile of a data set is a value such that at least p percent of the items take on this value or less and at least (100 - p) percent of the items take on this value or more. – Arrange the data in ascending order. – Compute index i, the position of the pth percentile. – i = (p/100)n – If i is not an integer, round up. The p th percentile is the value in the i th position. – If i is an integer, the p th percentile is the average of the values in positions i and i +1.
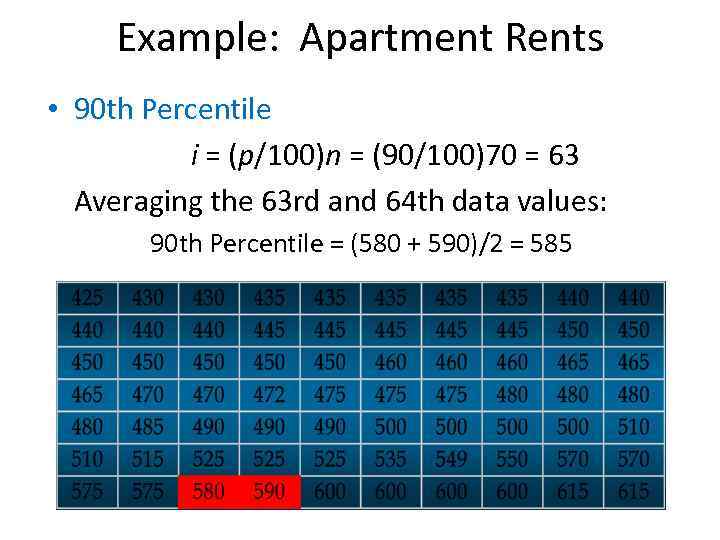 Example: Apartment Rents • 90 th Percentile i = (p/100)n = (90/100)70 = 63 Averaging the 63 rd and 64 th data values: 90 th Percentile = (580 + 590)/2 = 585
Example: Apartment Rents • 90 th Percentile i = (p/100)n = (90/100)70 = 63 Averaging the 63 rd and 64 th data values: 90 th Percentile = (580 + 590)/2 = 585
 Quartiles • Quartiles are specific percentiles • First Quartile = 25 th Percentile • Second Quartile = 50 th Percentile = =Median • Third Quartile = 75 th Percentile
Quartiles • Quartiles are specific percentiles • First Quartile = 25 th Percentile • Second Quartile = 50 th Percentile = =Median • Third Quartile = 75 th Percentile
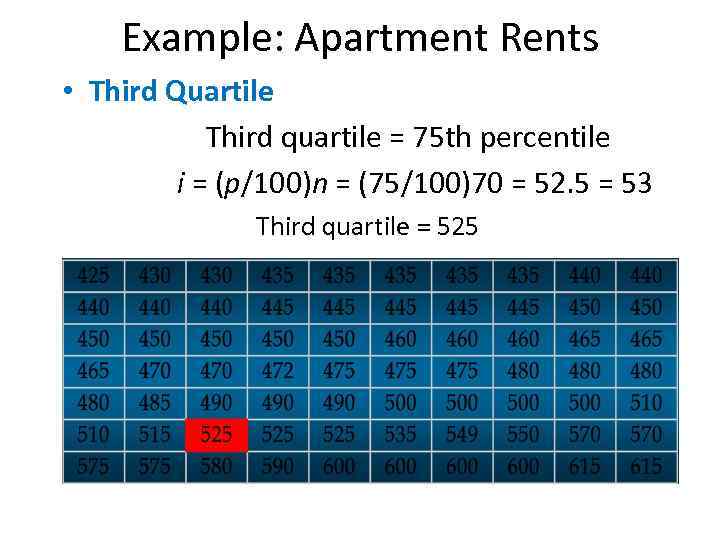 Example: Apartment Rents • Third Quartile Third quartile = 75 th percentile i = (p/100)n = (75/100)70 = 52. 5 = 53 Third quartile = 525
Example: Apartment Rents • Third Quartile Third quartile = 75 th percentile i = (p/100)n = (75/100)70 = 52. 5 = 53 Third quartile = 525
 Interquartile Range • The interquartile range of a data set is the difference between the third quartile and the first quartile. • It is the range for the middle 50% of the data. • It overcomes the sensitivity to extreme data values.
Interquartile Range • The interquartile range of a data set is the difference between the third quartile and the first quartile. • It is the range for the middle 50% of the data. • It overcomes the sensitivity to extreme data values.
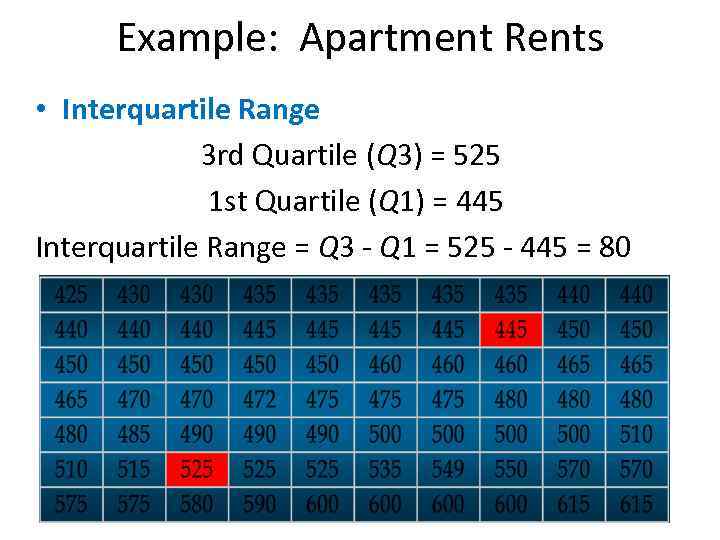 Example: Apartment Rents • Interquartile Range 3 rd Quartile (Q 3) = 525 1 st Quartile (Q 1) = 445 Interquartile Range = Q 3 - Q 1 = 525 - 445 = 80
Example: Apartment Rents • Interquartile Range 3 rd Quartile (Q 3) = 525 1 st Quartile (Q 1) = 445 Interquartile Range = Q 3 - Q 1 = 525 - 445 = 80
 • Variance and standard deviation Determine how far the observations are from their mean. Where: – = sample mean – x = values of the sample – n = sample size 13
• Variance and standard deviation Determine how far the observations are from their mean. Where: – = sample mean – x = values of the sample – n = sample size 13
 • Variance and standard deviation Determine how far the observations are from their mean. Where: μ = population mean x = values of the population N = population size 14
• Variance and standard deviation Determine how far the observations are from their mean. Where: μ = population mean x = values of the population N = population size 14
 • The variance is a measure of variability that utilizes all the data. • It is based on the difference between the value of each observation (xi) and the mean ( for a sample, m for a population).
• The variance is a measure of variability that utilizes all the data. • It is based on the difference between the value of each observation (xi) and the mean ( for a sample, m for a population).
 • Coefficient of variation – Measures the standard deviation relative to the mean. – It is expressed as a percentage. – Used to compare samples that are measured in different units. 16
• Coefficient of variation – Measures the standard deviation relative to the mean. – It is expressed as a percentage. – Used to compare samples that are measured in different units. 16
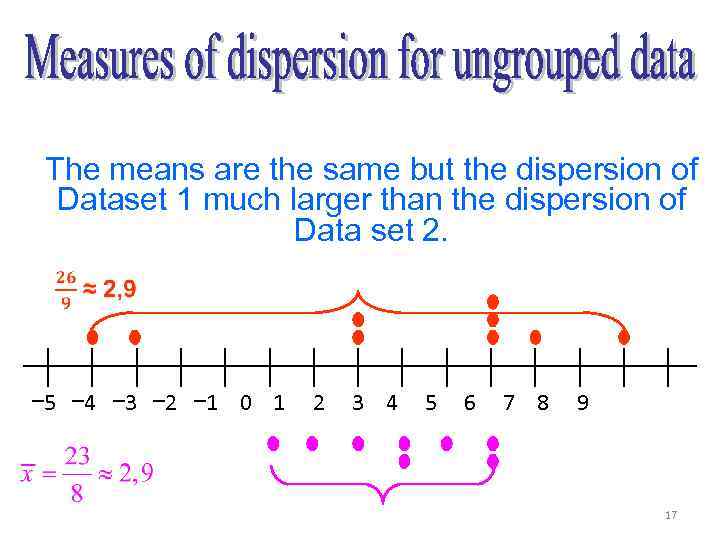 Example - Given the following data sets: means 2 same but 5 dispersion of the 5 st: 1 The -4 -3 are the 2 5 6 8 Dataset 1 much larger than the dispersion of 2 nd : 0 1 2 Data set 2. 4 3 3 5 5 − 4 − 3 − 2 − 1 0 1 2 3 4 5 6 7 8 9 17
Example - Given the following data sets: means 2 same but 5 dispersion of the 5 st: 1 The -4 -3 are the 2 5 6 8 Dataset 1 much larger than the dispersion of 2 nd : 0 1 2 Data set 2. 4 3 3 5 5 − 4 − 3 − 2 − 1 0 1 2 3 4 5 6 7 8 9 17
 Example – Given the following data sets: 1 st: − 4 − 3 2 2 5 5 5 6 2 nd : 0 1 2 3 3 4 5 8 5 The range of the measurements is given by: R = Largest value – smallest value R = 8 – (− 4) R = 5 − 0 R = 12 R = 5 18
Example – Given the following data sets: 1 st: − 4 − 3 2 2 5 5 5 6 2 nd : 0 1 2 3 3 4 5 8 5 The range of the measurements is given by: R = Largest value – smallest value R = 8 – (− 4) R = 5 − 0 R = 12 R = 5 18
 Example – Given the following data sets: 1 st: − 4 − 3 2 2 5 5 5 6 2 nd : 0 1 2 3 3 4 5 8 5 The MAD (mean absolute deviation) of the measurements is given by: MAD = 3, 23 MAD = 1, 4 19
Example – Given the following data sets: 1 st: − 4 − 3 2 2 5 5 5 6 2 nd : 0 1 2 3 3 4 5 8 5 The MAD (mean absolute deviation) of the measurements is given by: MAD = 3, 23 MAD = 1, 4 19
 Example – Given the following data sets: 1 st: − 4 − 3 2 2 5 5 5 6 8 2 nd: 0 1 2 3 3 4 5 5 he variance of the measurements is given by: 20
Example – Given the following data sets: 1 st: − 4 − 3 2 2 5 5 5 6 8 2 nd: 0 1 2 3 3 4 5 5 he variance of the measurements is given by: 20
 Example – Given the following data sets: 1 st: − 4 − 3 2 2 5 5 5 6 8 2 nd : 0 1 2 3 3 4 5 5 e standard deviation of the measurements is given 21
Example – Given the following data sets: 1 st: − 4 − 3 2 2 5 5 5 6 8 2 nd : 0 1 2 3 3 4 5 5 e standard deviation of the measurements is given 21
 • Consider another example, which will allow us even greater precision in measuring variability. Define the following sets: C = (0, 0, 1) and D = (99, 99, 100). These samples are characterized by the same variance (one element differs from the rest by 1; σC =σD =0, 5), but we clearly see that the "consequences" of this variability are much smaller for the set D than the "consequences" for the set C: a difference of one is not so important if the point of reference is 99 or 100 when compared to the same difference if the reference point is 0 or 1.
• Consider another example, which will allow us even greater precision in measuring variability. Define the following sets: C = (0, 0, 1) and D = (99, 99, 100). These samples are characterized by the same variance (one element differs from the rest by 1; σC =σD =0, 5), but we clearly see that the "consequences" of this variability are much smaller for the set D than the "consequences" for the set C: a difference of one is not so important if the point of reference is 99 or 100 when compared to the same difference if the reference point is 0 or 1.
 • Therefore, another measure of variability takes into account this aspect. This is the coefficient of variation, СV, (usually given as a percentage): • For the sets C and D, it is respectively: • СVC = 200 % and СVD = 0, 5 %. • This is the correct measure of the variability of these samples.
• Therefore, another measure of variability takes into account this aspect. This is the coefficient of variation, СV, (usually given as a percentage): • For the sets C and D, it is respectively: • СVC = 200 % and СVD = 0, 5 %. • This is the correct measure of the variability of these samples.
 Example – Given the following data sets: 1 st: − 4 − 3 2 2 5 5 5 6 2 nd : 0 1 2 3 3 4 5 8 5 The coefficient of variation of the measurements is given by: 24
Example – Given the following data sets: 1 st: − 4 − 3 2 2 5 5 5 6 2 nd : 0 1 2 3 3 4 5 8 5 The coefficient of variation of the measurements is given by: 24
 • Consider the samples: • A = (2, -2) and B = (1000000, -1000000). • The average value is the same for both samples and equal to 0. We already know that what differentiates between these samples is their variability: the standard deviation for sample A is σ =2, 8284, while for sample B the standard deviation is σ =1414214, i. e. 500, 000 times larger.
• Consider the samples: • A = (2, -2) and B = (1000000, -1000000). • The average value is the same for both samples and equal to 0. We already know that what differentiates between these samples is their variability: the standard deviation for sample A is σ =2, 8284, while for sample B the standard deviation is σ =1414214, i. e. 500, 000 times larger.
 • Variance and standard deviation (sample) Where: – f = frequencies of class intervals – x = class midpoints of class intervals – n = sample size 26
• Variance and standard deviation (sample) Where: – f = frequencies of class intervals – x = class midpoints of class intervals – n = sample size 26
 • Variance and standard deviation (population) Where: – f = frequencies of class intervals – x = class midpoints of class intervals – N = population size 27
• Variance and standard deviation (population) Where: – f = frequencies of class intervals – x = class midpoints of class intervals – N = population size 27
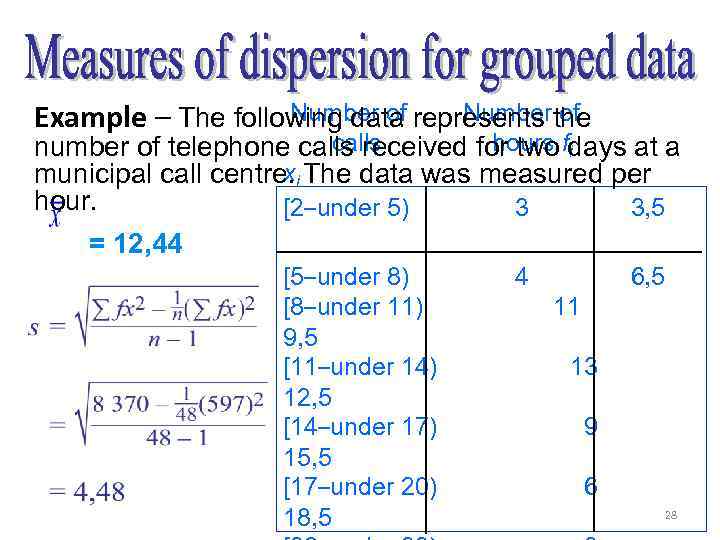 Number of Example – The following data represents the calls hours i number of telephone calls received for two fdays at a x municipal call centre. i The data was measured per hour. [2–under 5) 3 3, 5 = 12, 44 [5–under 8) [8–under 11) 9, 5 [11–under 14) 12, 5 [14–under 17) 15, 5 [17–under 20) 18, 5 4 6, 5 11 13 9 6 28
Number of Example – The following data represents the calls hours i number of telephone calls received for two fdays at a x municipal call centre. i The data was measured per hour. [2–under 5) 3 3, 5 = 12, 44 [5–under 8) [8–under 11) 9, 5 [11–under 14) 12, 5 [14–under 17) 15, 5 [17–under 20) 18, 5 4 6, 5 11 13 9 6 28
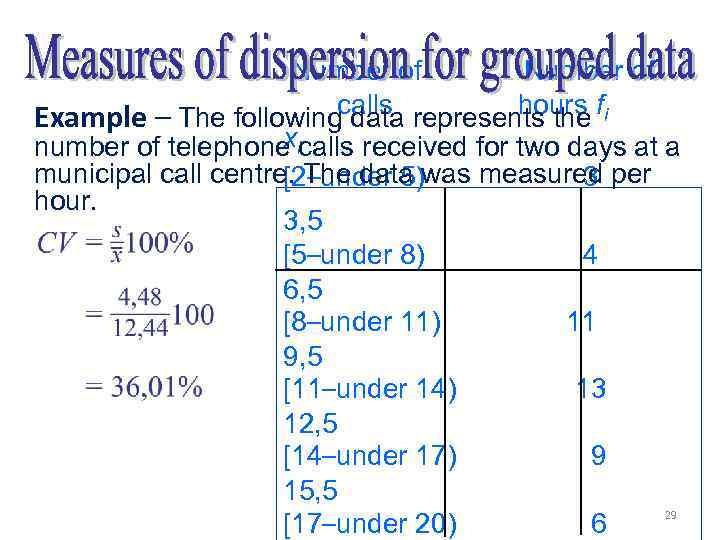 Number of hours Example – The followingcalls represents the fi data x number of telephone icalls received for two days at a municipal call centre. The data was measured per [2–under 5) 3 hour. 3, 5 [5–under 8) 4 6, 5 [8–under 11) 11 9, 5 [11–under 14) 13 12, 5 [14–under 17) 9 15, 5 29 [17–under 20) 6
Number of hours Example – The followingcalls represents the fi data x number of telephone icalls received for two days at a municipal call centre. The data was measured per [2–under 5) 3 hour. 3, 5 [5–under 8) 4 6, 5 [8–under 11) 11 9, 5 [11–under 14) 13 12, 5 [14–under 17) 9 15, 5 29 [17–under 20) 6
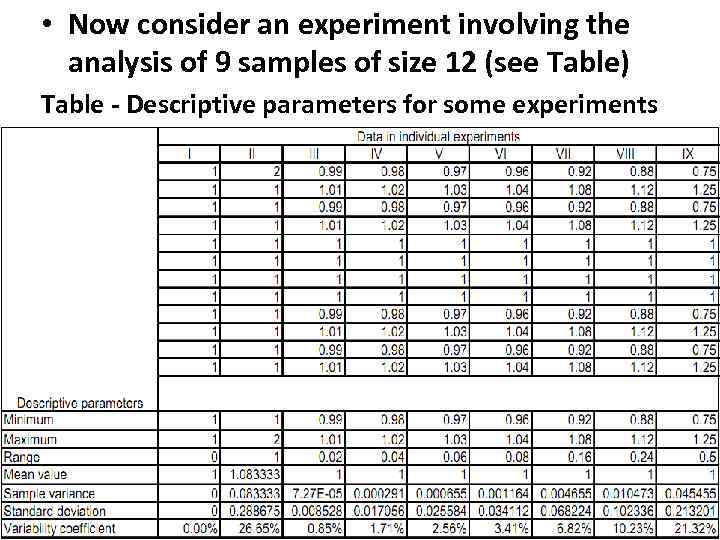 • Now consider an experiment involving the analysis of 9 samples of size 12 (see Table) Table - Descriptive parameters for some experiments
• Now consider an experiment involving the analysis of 9 samples of size 12 (see Table) Table - Descriptive parameters for some experiments
 CHARACTERISTICS OF THE VARIFNCE 1. If the individual characteristic of the values data decrease or increase on a constant number (A), the variance does not change.
CHARACTERISTICS OF THE VARIFNCE 1. If the individual characteristic of the values data decrease or increase on a constant number (A), the variance does not change.
 • 2. If the individual characteristic of the data values to divide or to multiply by a constant factor (A), then the variance decreases (or increases) in the square of a constant factor:
• 2. If the individual characteristic of the data values to divide or to multiply by a constant factor (A), then the variance decreases (or increases) in the square of a constant factor:
 • 3. Thus the sum of the squared deviations of the numbers in a data set from the mean is a minimum value :
• 3. Thus the sum of the squared deviations of the numbers in a data set from the mean is a minimum value :
 • 4. If a constant value equal to zero, then the variance is equal to the difference between the mean square of the data values and the square of the mean: or If A=0, then the following equality holds:
• 4. If a constant value equal to zero, then the variance is equal to the difference between the mean square of the data values and the square of the mean: or If A=0, then the following equality holds:
 • So, there is a second method of calculating the variance : • Where the mean of square values is :
• So, there is a second method of calculating the variance : • Where the mean of square values is :
 • The short-cut formula has been derived for calculating the sample variance. This is handy when the data being evaluated number more than a few items. This equation is the short-cut formula used to compute the sample variance. The sample standard deviation is computed by taking the square root of this variance.
• The short-cut formula has been derived for calculating the sample variance. This is handy when the data being evaluated number more than a few items. This equation is the short-cut formula used to compute the sample variance. The sample standard deviation is computed by taking the square root of this variance.
 Mean and variance of the alternative feature • Besides the variance of quantitative attributes it is often necessary to determine the variation of qualitative or altérnative attributes. • An alternative attribute is an attribute that can have only two values: the occurrence or non-occurrence of the event. • In practice, for example, it is studied the quality of manufactured products by splitting it into a qualitative or defective.
Mean and variance of the alternative feature • Besides the variance of quantitative attributes it is often necessary to determine the variation of qualitative or altérnative attributes. • An alternative attribute is an attribute that can have only two values: the occurrence or non-occurrence of the event. • In practice, for example, it is studied the quality of manufactured products by splitting it into a qualitative or defective.
 Mean and variance of the alternative feature • Alternate attribute takes the value 1 if the event occurred. And it is equal to 0, if the event did not occurred. • The share values of the attribute for which the event occurred. We will denote as p, and if it do not come - as q. p + q = 1
Mean and variance of the alternative feature • Alternate attribute takes the value 1 if the event occurred. And it is equal to 0, if the event did not occurred. • The share values of the attribute for which the event occurred. We will denote as p, and if it do not come - as q. p + q = 1
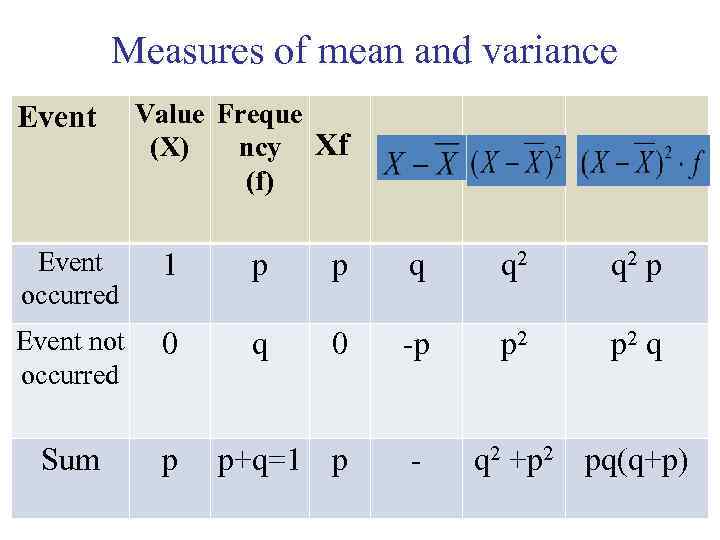 Measures of mean and variance Event Value Freque (Х) ncy Xf (f) Event occurred 1 p p q q 2 p Event not occurred 0 q 0 -p p 2 q Sum p p+q=1 p - q 2 +p 2 pq(q+p)
Measures of mean and variance Event Value Freque (Х) ncy Xf (f) Event occurred 1 p p q q 2 p Event not occurred 0 q 0 -p p 2 q Sum p p+q=1 p - q 2 +p 2 pq(q+p)
 • Mean of the alternative sign : • where р – share of the units that have an attribute; • q - share of the units which have not an attribute.
• Mean of the alternative sign : • where р – share of the units that have an attribute; • q - share of the units which have not an attribute.
 • Variance of the alternative feature: Variance • The standard deviation:
• Variance of the alternative feature: Variance • The standard deviation:
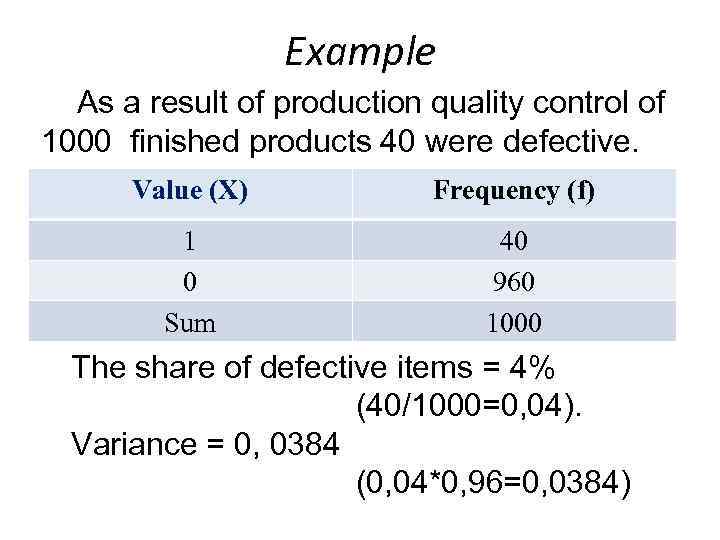 Example As a result of production quality control of 1000 finished products 40 were defective. Value (X) Frequency (f) 1 0 Sum 40 960 1000 The share of defective items = 4% (40/1000=0, 04). Variance = 0, 0384 (0, 04*0, 96=0, 0384)
Example As a result of production quality control of 1000 finished products 40 were defective. Value (X) Frequency (f) 1 0 Sum 40 960 1000 The share of defective items = 4% (40/1000=0, 04). Variance = 0, 0384 (0, 04*0, 96=0, 0384)
 • Further Measures of variations you have calculated independently
• Further Measures of variations you have calculated independently
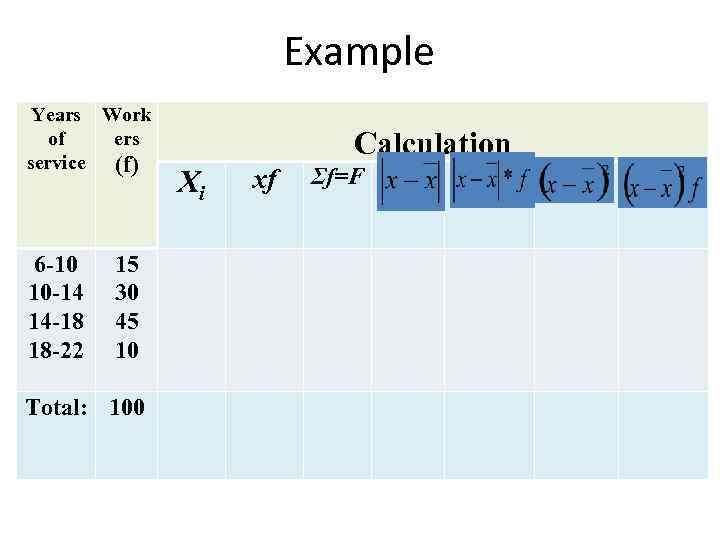 Example Years Work of ers service (f) 6 -10 10 -14 14 -18 18 -22 15 30 45 10 Calculation Хi xf Σf=F Total: 100
Example Years Work of ers service (f) 6 -10 10 -14 14 -18 18 -22 15 30 45 10 Calculation Хi xf Σf=F Total: 100
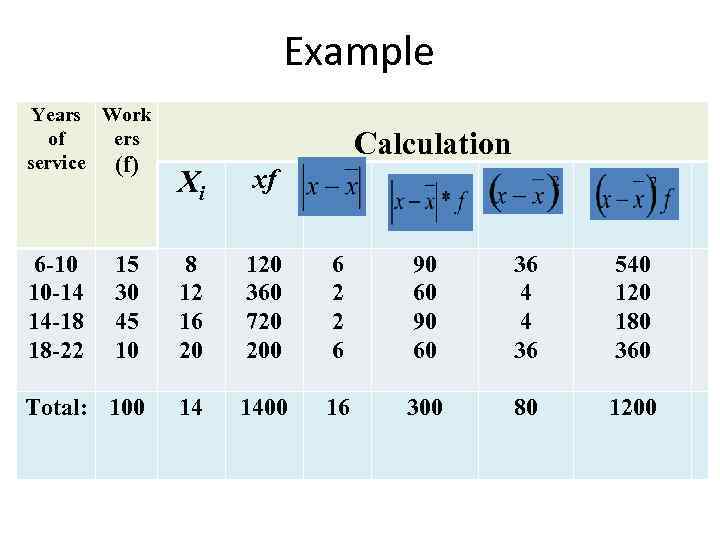 Example Years Work of ers service (f) Calculation Хi xf 15 30 45 10 8 12 16 20 120 360 720 200 6 2 2 6 90 60 36 4 4 36 540 120 180 360 Total: 100 14 1400 16 300 80 1200 6 -10 10 -14 14 -18 18 -22
Example Years Work of ers service (f) Calculation Хi xf 15 30 45 10 8 12 16 20 120 360 720 200 6 2 2 6 90 60 36 4 4 36 540 120 180 360 Total: 100 14 1400 16 300 80 1200 6 -10 10 -14 14 -18 18 -22
 Calculation: • Range: R = 22 -6 =16 (years) • mean: • MAD: • Variance: σ2 • Standard deviation: σ • CV
Calculation: • Range: R = 22 -6 =16 (years) • mean: • MAD: • Variance: σ2 • Standard deviation: σ • CV


