Part 1 Positive Equality for Uninterpreted functions in

Part 1: Positive Equality for Uninterpreted functions in Eager Encoding

Eliminating Function applications n Two applications of an uninterpreted function f in a formula n f(x 1) and f(x 2) Ackermann’s Encoding Bryant, German, Velev’s Encoding f(x 1) vf 1 f(x 1) f(x 2) vf 2 f(x 2) x 1= x 2 vf 1 = vf 2 – 2– vf 1 ITE(x 1= x 2, vf 1, vf 2)

Positive Equality Optimization Goal n Replace as many of the vfi variables with constant values Exploit the positive structure of the formula Overall Benefit n n – 3– The function-free formula has smaller number of integer variables Reduces the number of interpretations to check for validity

Eliminating Function applications n Two applications of an uninterpreted function f in a formula n f(x 1) and f(x 2) Ackermann’s Encoding Bryant, German, Velev’s Encoding f(x 1) vf 1 f(x 1) f(x 2) vf 2 f(x 2) x 1= x 2 vf 1 = vf 2 – 4– vf 1 ITE(x 1= x 2, vf 1, vf 2) Favors positive equality analysis

EUF n Logic of Equality with Uninterpreted Functions Terms ITE(F, T 1, T 2) f (T 1, …, Tk) If-then-else Function application Formulas F, F 1 F 2 Boolean connectives T 1 = T 2 Equation p (T 1, …, Tk) Predicate application Special Cases v a – 5– Domain variable (order-0 function) Propositional variable (order-0 predicate)

EUF and small-model property Small Model Property for Validity [Ackermann ’ 54] n n Suffices to consider a domain with k values n k is the number of distinct function application terms in the formula Number of cases (interpretations) to check: k! Function-application terms: {x, y, g(x), g(y), f(g(x), f(g(y) } = f = x g f g y (x=y) (f(g(x)) = f(g(y)) k=6 – 6–

Positive Equality for EUF [Bryant, German, Velev CAV’ 99] General (g) Functions x, y Classify formulas, terms, functions into l Positive (p) l General (g) = p-formulas Positive (p) formulas l Negated even no. of times l Do not control ITE Positive (p) terms l l f f p-terms = g g g-formulas Never appears in a g-formula equation Positive (p) function symbols – 7– Positive (p) Functions f, g All applications are p-terms x y (x=y) (f(g(x)) = f(g(y))

Maximally Diverse Interpretations An interpretation I is maximally diverse if: n For any p-function symbol f 1. I [f(T 1) = f(T 2)] iff I [T 1=T 2] 2. I [f(T)] I [g(U)], for any other function symbol g where f(T 1), f(T 2), g(U) are terms in the formula = g h = g g x y – 8– Terms h x g (x) Equal? y g (y) y Potentially Only if x = y No

Maximally Diverse Interpretations An interpretation I is maximally diverse if: n For any p-function symbol f 1. I [f(T 1) = f(T 2)] iff I [T 1=T 2] 2. I [f(T 1)] I [g(U)], for any other function symbol g where f(T 1), f(T 2), g(U) are terms in the formula Property n – 9– Formula valid if and only if true under all maximally diverse interpretations

Justification of Maximal Diversity Property = g Create Worst Case for Validity n n n h = g g h x y Falsify positive equation Function applications yield distinct results Function arguments distinct For a formula F n – 10 – For any interpretation I, there is a maximally diverse interpretation J, such that J[F] I[F]

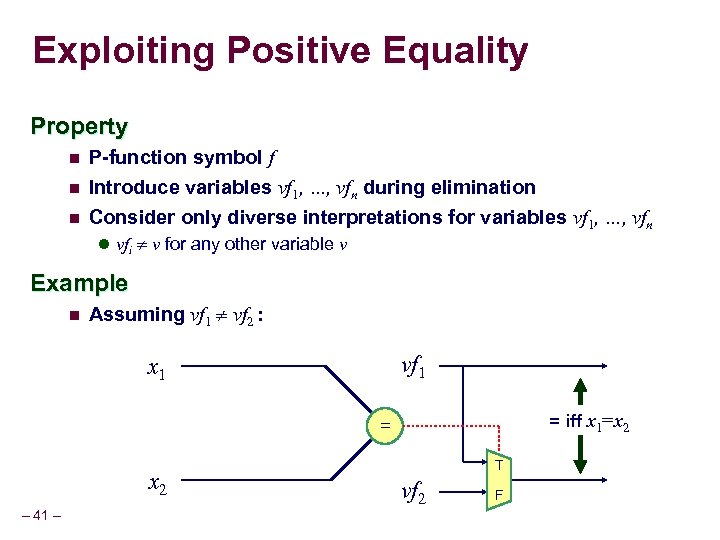
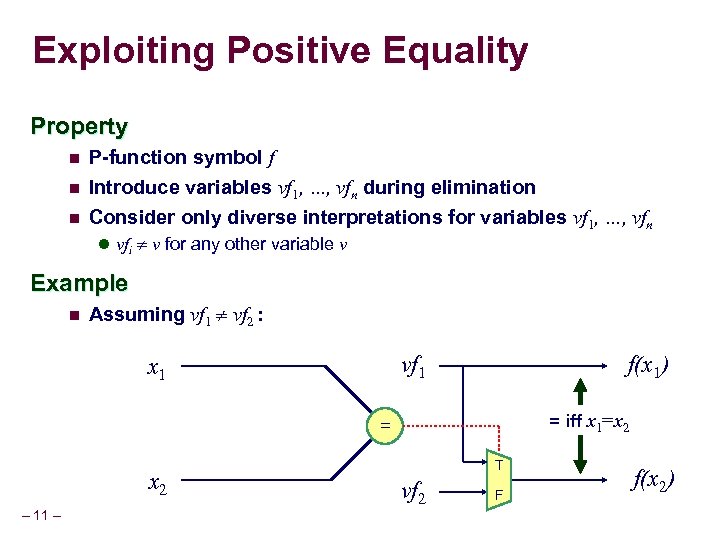Exploiting Positive Equality Property n n n P-function symbol f Introduce variables vf 1, …, vfn during elimination Consider only diverse interpretations for variables vf 1, …, vfn l vfi v for any other variable v Example n Assuming vf 1 vf 2 : f(x 1) vf 1 x 1 = iff x 1=x 2 = x 2 – 11 – T vf 2 F f(x 2)

Summary: Positive equality optimization 1. Eliminate function applications 1. Introduce vf 1, …, vfn while eliminating function symbol f 2. For a p-function symbol f 1. Replace vf 1, …, vfn with distinct constants 3. The only variables in the function-free formula are the vfi variables for g function symbols n m = number of g-function applications – 12 –

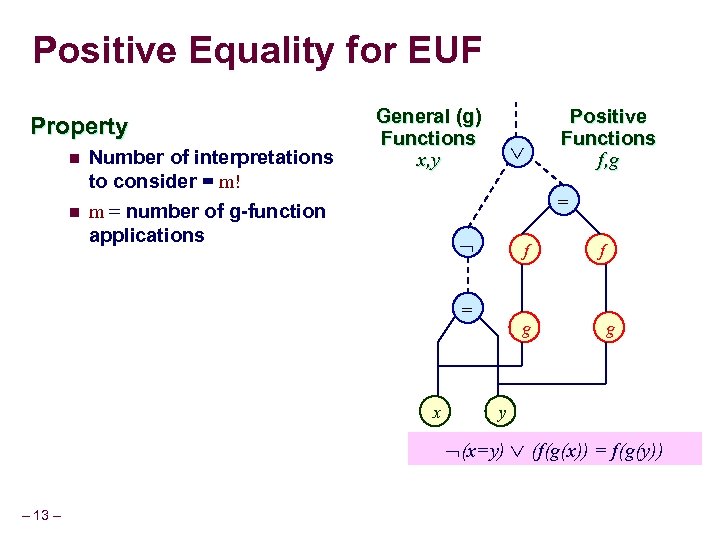Positive Equality for EUF Property n n Number of interpretations to consider = m! m = number of g-function applications General (g) Functions x, y Positive Functions f, g = f = x g f g y (x=y) (f(g(x)) = f(g(y)) – 13 –

Positive Equality for EUF General (g) Functions x, y Property n n Number of interpretations to consider = m! m = number of g-function applications Positive Functions f, g Function-application terms: {x, y, g(x), g(y), f(g(x)), f(g(y)) } p applications: {g(x), g(y), f(g(x)), f(g(y)) } g applications: {x, y} m=2 (x=y) (f(g(x)) = f(g(y)) Search Space reduced from 6! to 2! – 14 –

Application of positive equality Pipelined processor verification l Bryant, German and Velev CAV’ 99, Velev and Bryant DAC’ 00, . . n Observation: Most uninterpreted functions which appear in pipeline data-path are p-functions l E. g. ALU, Incrementer for PC, …. Other Infinite-state system verification l Bryant, Lahiri, Seshia CAV’ 02 n – 15 – Improves efficiency in benchmarks from cache-coherence verification, out-of-order processors, software benchmarks

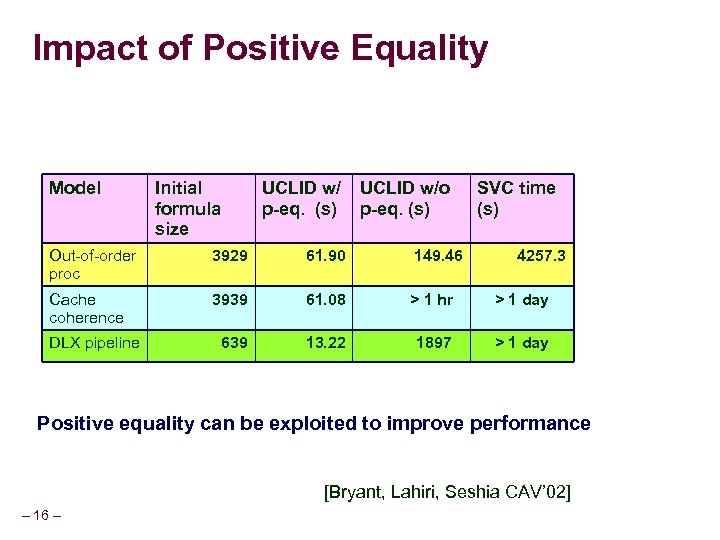Impact of Positive Equality Model Initial formula size UCLID w/ p-eq. (s) UCLID w/o p-eq. (s) SVC time (s) Out-of-order proc 3929 61. 90 149. 46 Cache coherence 3939 61. 08 > 1 hr > 1 day 639 13. 22 1897 > 1 day DLX pipeline 4257. 3 Positive equality can be exploited to improve performance [Bryant, Lahiri, Seshia CAV’ 02] – 16 –

Ackermann’s encoding and positive equality n Two applications of an uninterpreted function f in a formula n f(x 1) and f(x 2) Can’t assign distinct values to vf 1, vf 2 for p-function symbol f Ackermann’s Encoding n f(x 1) vf 1 f(x 2) vf 2 x 1= x 2 vf 1 = vf 2 – 17 – Ignores the case when x 1= x 2

Limitation of positive equality analysis Limitation of previous approach n Not “robust” General Functions x, f l Entire analysis fails even Positive Functions = when a single application is negative f f f Function-application terms: {x, f(x), f 2(x), f 3(x), f 4(x) } p-applications: {} – 18 – g-applications: {x, f(x), f 2(x), f 3(x), f 4(x) } = f x (f(x)=x) (f(f(x)))) = f(f(f((x)))

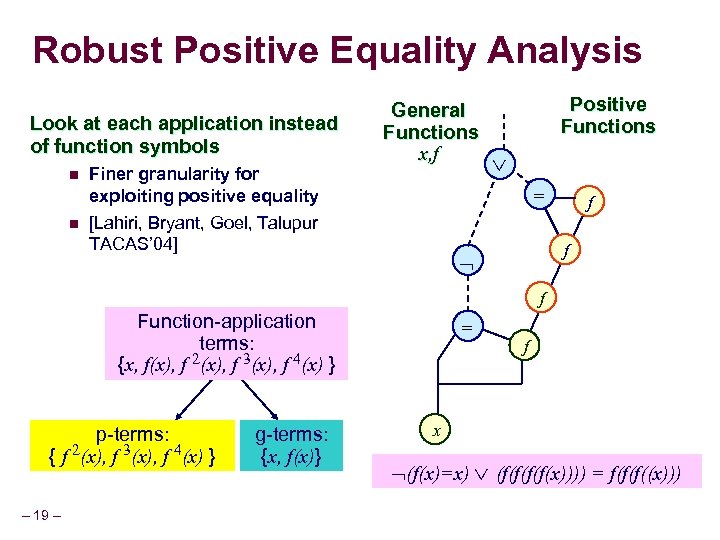Robust Positive Equality Analysis Look at each application instead of function symbols n n Finer granularity for exploiting positive equality General Functions x, f Positive Functions = [Lahiri, Bryant, Goel, Talupur TACAS’ 04] f f f Function-application terms: {x, f(x), f 2(x), f 3(x), f 4(x) } p-terms: 2(x), f 3(x), f 4(x) } {f – 19 – g-terms: {x, f(x)} = f x (f(x)=x) (f(f(x)))) = f(f(f((x)))

Robust Positive Equality Analysis Goal n If a variable vfi is a result of eliminating a p-term, then try to assign it a distinct constant Question n Can we always assign the vfi variables for any p-term a distinct value? l Not always n Can we compute the set of p-terms that maximizes the number of vfi variables that can be assigned distinct values? l In general, NP-complete – 20 –

Outline Robust positive equality n “Robust” maximal diversity theorem Exploiting robust positive equality n n Obstacles Solutions Results Related work – 21 –

Robust Maximal Diversity For an interpretation I n A p-term f(T) is called is g-arg-distinct, if there is no g-term f(U), such that I [T] = I [U]. An interpretation I is robust maximally diverse if: n For every g-arg-distinct p-term f(T 1), 1. I [f(T 1) = f(T 2)] iff I [T 1=T 2] 2. I [f(T)] I [g(U)], for any other function symbol g where f(T 1), f(T 2), g(U) are terms in the formula – 22 –

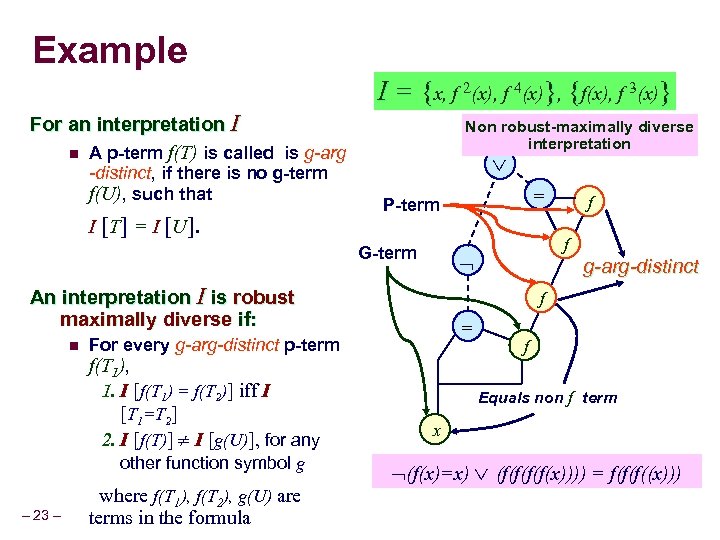Example I = {x, f 2(x), f 4(x)}, {f(x), f 3(x)} For an interpretation I n A p-term f(T) is called is g-arg -distinct, if there is no g-term f(U), such that I [T] = I [U]. Non robust-maximally diverse interpretation G-term – 23 – For every g-arg-distinct p-term f(T 1), 1. I [f(T 1) = f(T 2)] iff I [T 1=T 2] 2. I [f(T)] I [g(U)], for any other function symbol g where f(T 1), f(T 2), g(U) are terms in the formula f f An interpretation I is robust maximally diverse if: n = P-term g-arg-distinct f = f Equals non f term x (f(x)=x) (f(f(x)))) = f(f(f((x)))

Robust Maximal Diversity Theorem n Formula valid if and only if true under all robust maximally diverse interpretations Generalization of positive equality n Any robust-maximally diverse interpretation is a maximally diverse interpretations l The subset inclusion can be proper Consequence n – 24 – Fewer interpretations to consider to check validity

Exploiting Robust Positive Equality n Function applications f(x 1), …, f(xn) n Introduce variables vf 1, …, vfn during elimination f(x 1), …, f(xl), …, f(xi), …, f(xn) Contains all the g-terms for f Value of vfi = Value of f(xi) n when xi does not equal {x 1, …, xi-1} n – 25 – i. e. when f(xi) is g-arg-distinct By Robust maximal diversity theorem n Assign a distinct constant to vfi , when i>l

What we need Eliminate the g-terms as early as possible n n Constrained by the sub-expression ordering e. g. f(x) has to be eliminated before eliminating f(f (x)) Need the best topological order n Respects the sub-expression orderings n Maximizes the number of vf variables that can be assigned distinct constant value l Need to define this objective function precisely – 26 –

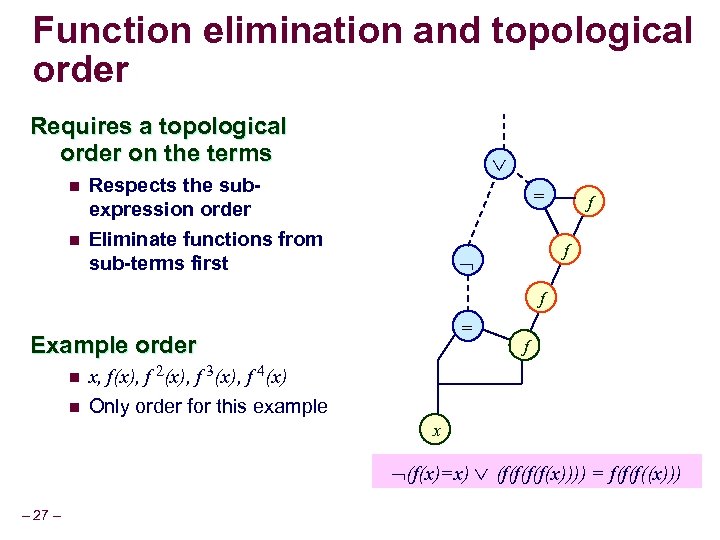Function elimination and topological order Requires a topological order on the terms n n Respects the subexpression order Eliminate functions from sub-terms first = f f f = Example order n x, f(x), f 2(x), f 3(x), f 4(x) n f Only order for this example x (f(x)=x) (f(f(x)))) = f(f(f((x))) – 27 –

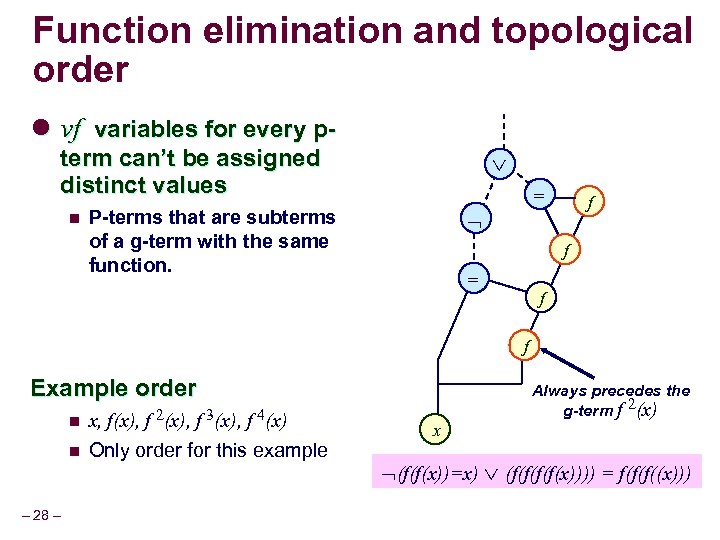Function elimination and topological order l vf variables for every pterm can’t be assigned distinct values n = P-terms that are subterms of a g-term with the same function. f f = f f Example order n n – 28 – x, f(x), f 2(x), f 3(x), f 4(x) Only order for this example x Always precedes the g-term f 2(x) (f(f(x))=x) (f(f(x)))) = f(f(f((x)))

Topological ordering and the p-terms n Topological order < Pos<(f) n Set of p-terms of f which do not precede any gterms of f in < Pos< = f Pos<(f) – 29 –

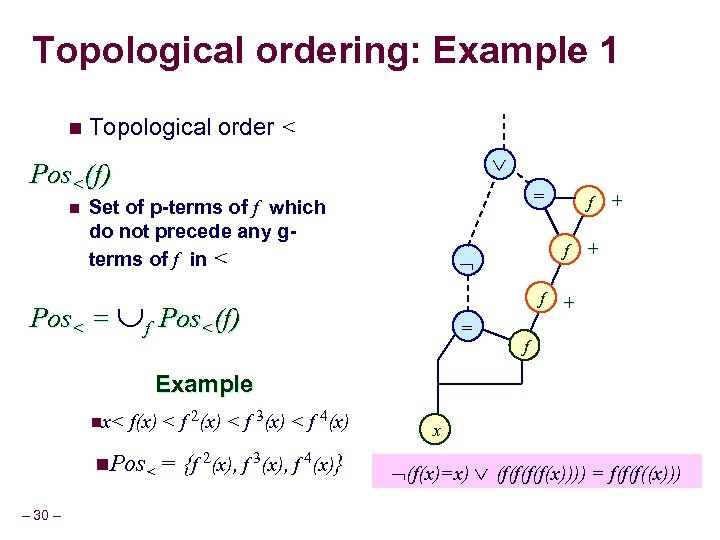Topological ordering: Example 1 n Topological order < Pos<(f) n = Set of p-terms of f which do not precede any gterms of f in < f + f + Pos< = f Pos<(f) = f Example nx< f(x) < f 2(x) < f 3(x) < f 4(x) n. Pos< = {f 2(x), f 3(x), f 4(x)} – 30 – x (f(x)=x) (f(f(x)))) = f(f(f((x)))

Topological ordering n Topological order < Property l Pos<(f) n Set of p-terms of f which do not precede any gterms of f in < Pos< = f Pos<(f) – 31 – The vfi variables which results when eliminating terms in Pos< can be assigned a distinct constant value Goal l Find the topological order “<” that maximizes the size of Pos<

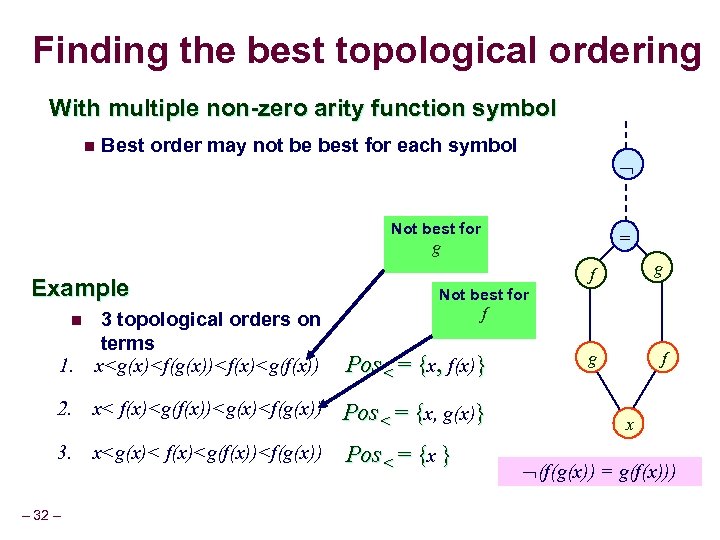Finding the best topological ordering With multiple non-zero arity function symbol n Best order may not be best for each symbol Not best for = g Example f f f 1. 2. x< f(x)

Obtaining best topological order Complexity n NP-complete l Polynomial when only 1 non-zero arity function symbol n Reduction from the maximum independent set problem Greedy heuristic to find a good order n n – 33 – Assign higher priorities to p-terms of functions with greater number of “potential” terms in Pos< Finds the optimal order for most of the examples we have seen so far.

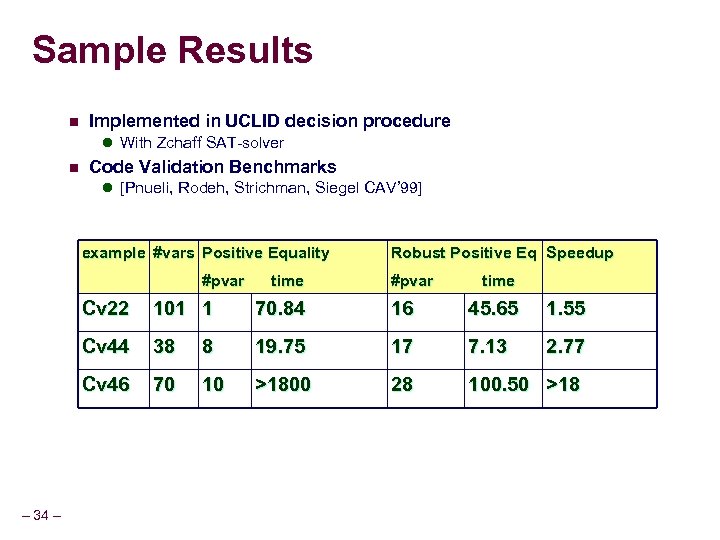Sample Results n Implemented in UCLID decision procedure l With Zchaff SAT-solver n Code Validation Benchmarks l [Pnueli, Rodeh, Strichman, Siegel CAV’ 99] example #vars Positive Equality #pvar time Robust Positive Eq Speedup #pvar time Cv 22 70. 84 16 45. 65 1. 55 Cv 44 38 8 19. 75 17 7. 13 2. 77 Cv 46 – 34 – 101 1 70 10 >1800 28 100. 50 >18

Observations Robust positive equality improves efficiency n Useful in practice Small overhead (+5%) over positive equality analysis n n – 35 – Efficient implementation can further reduce this overhead Seldom affects total time when translation time to SAT is a small fraction of the overall time

Related work Pnueli, Rodeh, Strichman & Siegel CAV’ 99 n Removes function applications by Ackermann’s reduction n Range allocation for the resultant formula l Assigns smaller ranges for g-terms Rodeh & Strichman CAV’ 01 n n – 36 – Uses Bryant, German & Velev’s function elimination method + range allocation Has similarities and differences with our work

Conclusions Positive Equality n Simplifies function-free formula by reducing the number of variables in the formula Robust Positive Equality n n Generalization of positive equality Improves applicability for more general benchmarks Can be extended for CLU logic n n – 37 – T 1 < T 2 + c [BLS 02; Lahiri MS Thesis] Can we generalize it for linear arithmetic + EUF?

Questions – 38 –

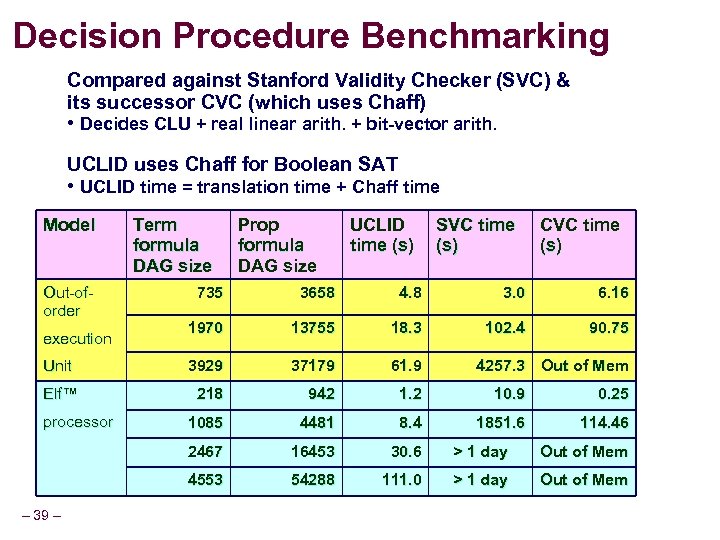Decision Procedure Benchmarking Compared against Stanford Validity Checker (SVC) & its successor CVC (which uses Chaff) • Decides CLU + real linear arith. + bit-vector arith. UCLID uses Chaff for Boolean SAT • UCLID time = translation time + Chaff time Model Out-oforder Term formula DAG size Prop formula DAG size UCLID time (s) SVC time (s) CVC time (s) 735 3658 4. 8 3. 0 6. 16 1970 13755 18. 3 102. 4 90. 75 Unit 3929 37179 61. 9 Elf™ 218 942 1. 2 10. 9 0. 25 1085 4481 8. 4 1851. 6 114. 46 2467 16453 30. 6 > 1 day Out of Mem 4553 54288 111. 0 > 1 day Out of Mem execution processor – 39 – 4257. 3 Out of Mem

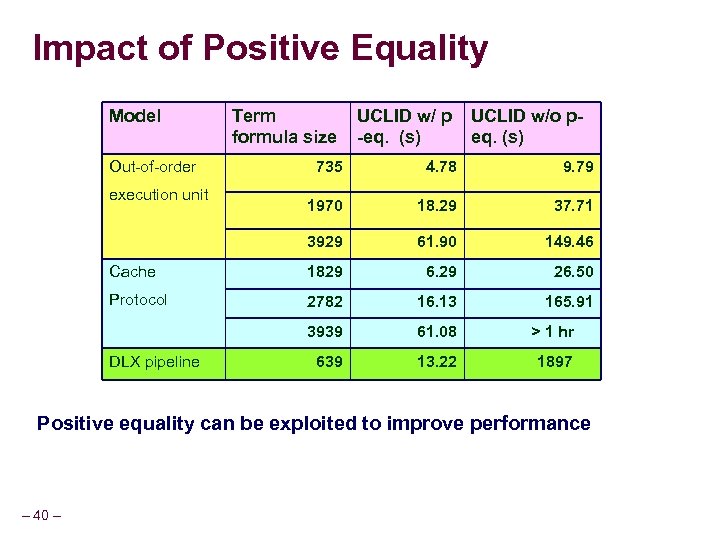Impact of Positive Equality Model Out-of-order Term formula size UCLID w/ p -eq. (s) UCLID w/o peq. (s) 735 4. 78 9. 79 1970 18. 29 37. 71 3929 61. 90 149. 46 Cache 1829 6. 29 26. 50 Protocol 2782 16. 13 165. 91 3939 61. 08 > 1 hr 639 13. 22 1897 execution unit DLX pipeline Positive equality can be exploited to improve performance – 40 –

Exploiting Positive Equality Property n n n P-function symbol f Introduce variables vf 1, …, vfn during elimination Consider only diverse interpretations for variables vf 1, …, vfn l vfi v for any other variable v Example n Assuming vf 1 vf 2 : vf 1 x 1 = iff x 1=x 2 = x 2 – 41 – T vf 2 F

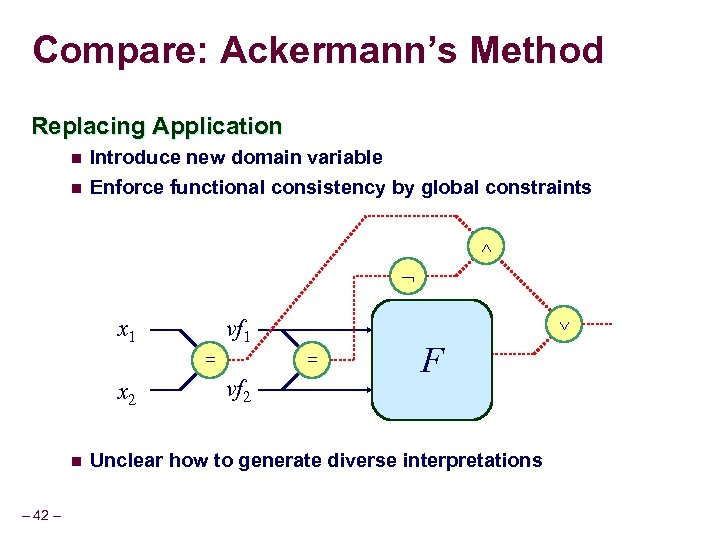Compare: Ackermann’s Method Replacing Application n Introduce new domain variable n Enforce functional consistency by global constraints x 1 = x 2 n – 42 – vf 1 f = vf 2 f F Unclear how to generate diverse interpretations

Decision Procedures in Verification Work-horse for many automated verification methodologies n Processor and Protocol verification l Pipelined processor verification » Burch & Dill CAV’ 94, Bryant, German & Velev CAV’ 99, … l Out-of-order processor and cache coherence verification » Lahiri, Seshia & Bryant FMCAD’ 02, Bryant, Lahiri & Seshia CAV’ 02 n Predicate abstraction l Software verification » SLAM (MSR), BLAST (Berkeley), MAGIC (CMU), … l Protocol verification » Das, Dill & Park CAV’ 99, – 43 –

Decision Procedures for quantifierfree fragment of first-order logic Principal theories n n Logic of equality with uninterpreted functions l f(x) = f(g(y)) Linear arithmetic l Difference-bound logic subset ( T 1 < T 2 + c) l Full linear arithmetic n Arrays l read and write operations Tools n n n – 44 – SVC/CVC from Stanford (FMCAD ’ 96, CAV’ 02, CAV ‘ 04) UCLID from CMU (CAV’ 02, CAV’ 04) ICS from SRI (CAV ’ 01) Simplify/Verifun from HP (CAV ’ 03) Zapato from Microsoft (CAV ’ 04) ……

Revisiting Positive Equality Shuvendu K. Lahiri Randal E. Bryant Amit Goel Muralidhar Talupur Carnegie Mellon University

Conclusions Generalization of Bryant et al’s positive equality analysis n Subsumes original positive equality Exploiting robust positive equality in a decision procedure n Problems and heuristics Future Work n Integrate smaller range-allocation for the g-terms l Pnueli et al. CAV’ 99, Talupur et al. CAV’ 04 – 46 –

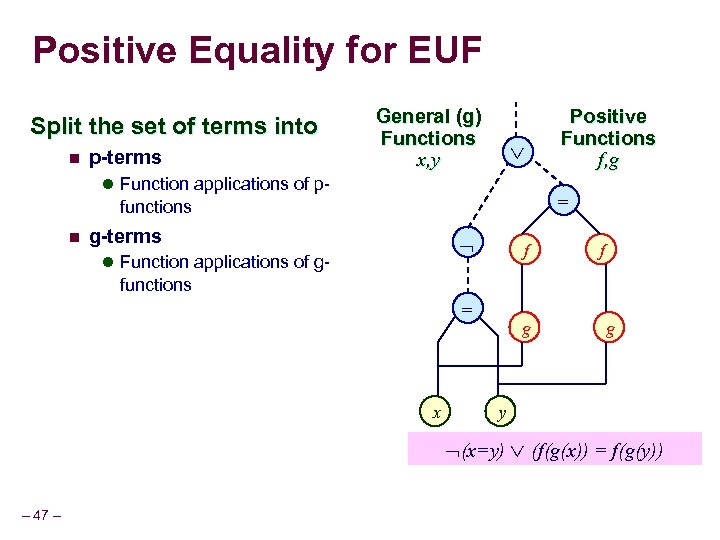Positive Equality for EUF Split the set of terms into n p-terms General (g) Functions x, y l Function applications of p- = functions n Positive Functions f, g g-terms l Function applications of g- f f functions = x g g y (x=y) (f(g(x)) = f(g(y)) – 47 –

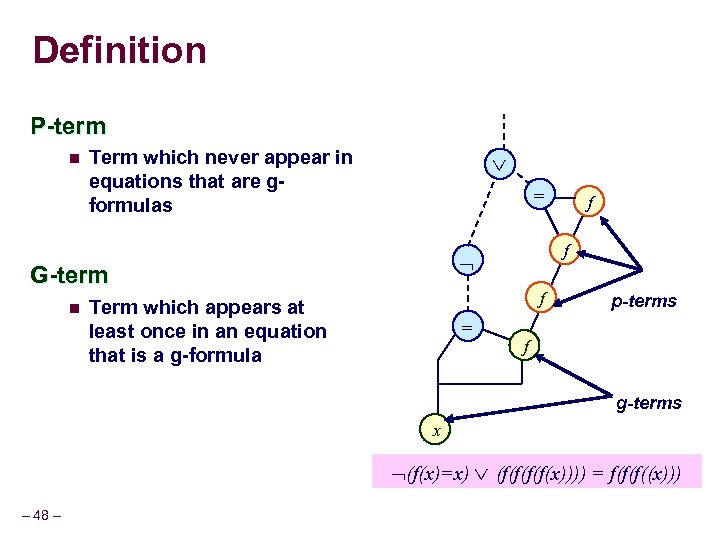Definition P-term n Term which never appear in equations that are gformulas = n f G-term f Term which appears at least once in an equation that is a g-formula = f p-terms f g-terms x (f(x)=x) (f(f(x)))) = f(f(f((x))) – 48 –

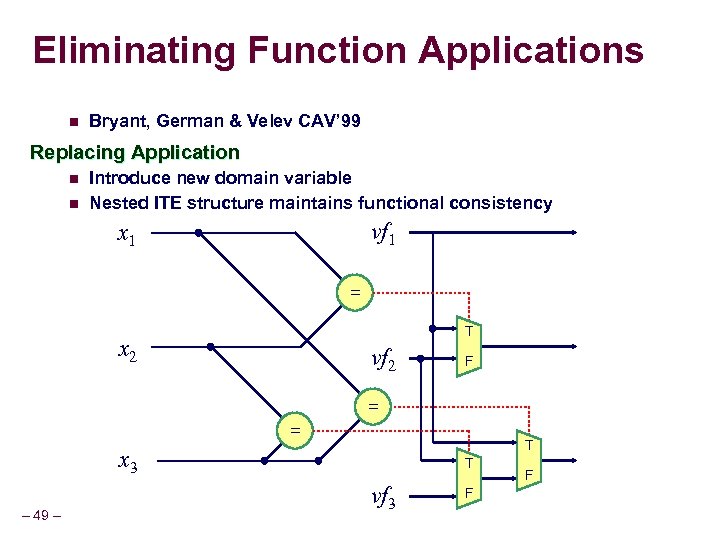Eliminating Function Applications n Bryant, German & Velev CAV’ 99 Replacing Application n n Introduce new domain variable Nested ITE structure maintains functional consistency f vf 1 x 1 = f vf x 2 T 2 F = = x 3 – 49 – T f T vf 3 F F

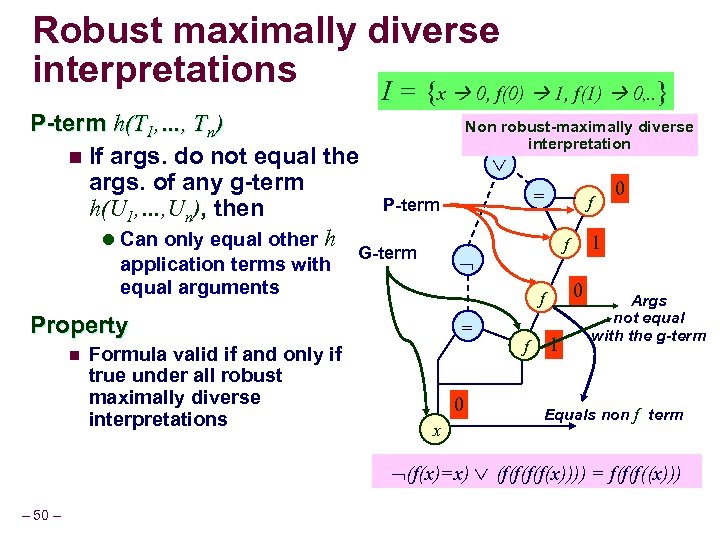Robust maximally diverse interpretations I = {x 0, f(0) 1, f(1) 0, . . } P-term h(T 1, …, Tn) n If args. do not equal the args. of any g-term h(U 1, …, Un), then l Can only equal other h application terms with equal arguments Non robust-maximally diverse interpretation P-term G-term Formula valid if and only if true under all robust maximally diverse interpretations f 0 f = 0 x f 1 0 1 f Property n = Args not equal with the g-term Equals non f term (f(x)=x) (f(f(x)))) = f(f(f((x))) – 50 –

Heuristic for obtaining topological order Potentially positive terms for a function f n The p-terms of f that are not sub-terms of any g-term of f Steps 1. 2. Sort the function symbols by the number of potentially positive terms For each function f in sorted order: n Put all the g-terms of f (and their subterms) in the topological order 3. – 51 – Put all the remaining pterms in the topological order

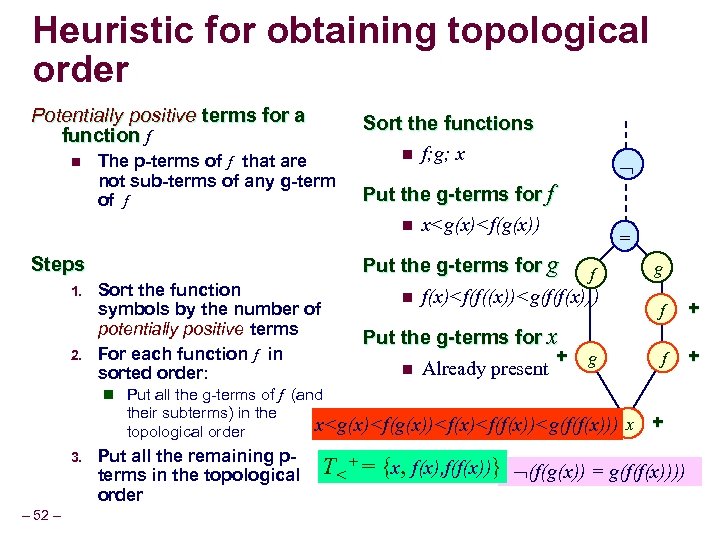Heuristic for obtaining topological order Potentially positive terms for a function f n The p-terms of f that are not sub-terms of any g-term of f 2. Put the g-terms for f n x

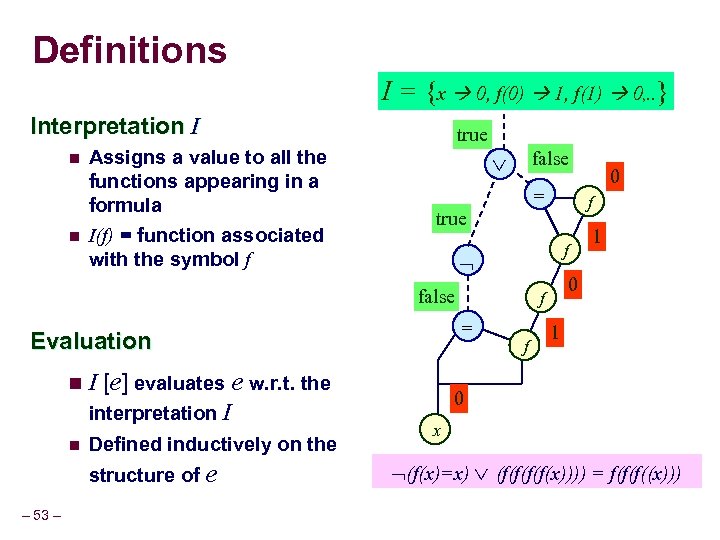Definitions I = {x 0, f(0) 1, f(1) 0, . . } Interpretation I n n Assigns a value to all the functions appearing in a formula I(f) = function associated with the symbol f true false = f n. I n Defined inductively on the structure of e – 53 – f 1 0 f = Evaluation [e] evaluates e w. r. t. the interpretation I f true false 0 1 0 x (f(x)=x) (f(f(x)))) = f(f(f((x)))

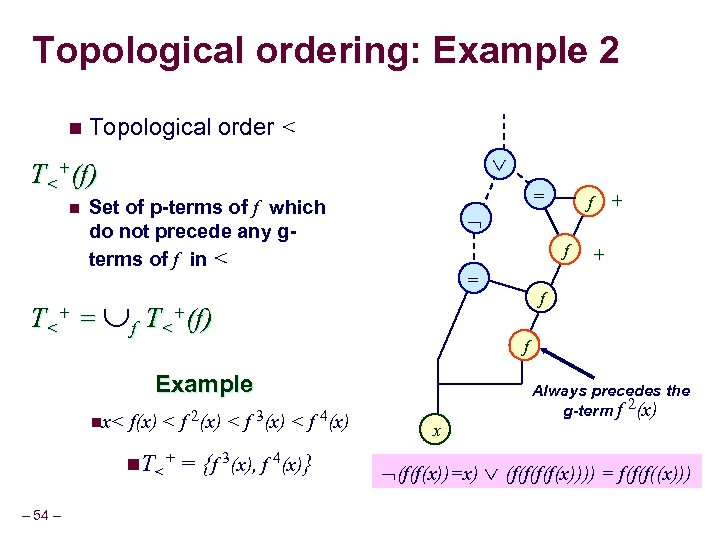Topological ordering: Example 2 n Topological order < T<+(f) n = Set of p-terms of f which do not precede any gterms of f in < f = T<+ = f T<+(f) f(x) < f 2(x) < f 3(x) < f 4(x) n. T<+ = {f 3(x), f 4(x)} – 54 – + f f Example nx< f + x Always precedes the g-term f 2(x) (f(f(x))=x) (f(f(x)))) = f(f(f((x)))

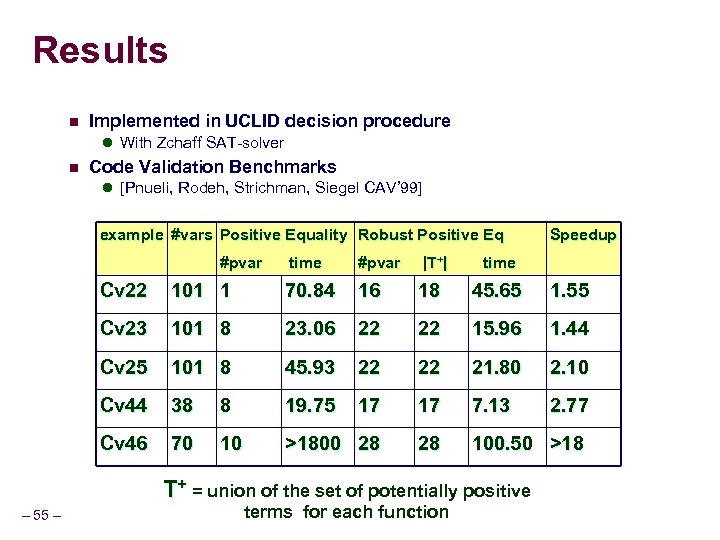Results n Implemented in UCLID decision procedure l With Zchaff SAT-solver n Code Validation Benchmarks l [Pnueli, Rodeh, Strichman, Siegel CAV’ 99] example #vars Positive Equality Robust Positive Eq #pvar time #pvar |T+| Speedup time Cv 22 101 1 70. 84 16 18 45. 65 1. 55 Cv 23 101 8 23. 06 22 22 15. 96 1. 44 Cv 25 101 8 45. 93 22 22 21. 80 2. 10 Cv 44 38 8 19. 75 17 17 7. 13 2. 77 Cv 46 70 10 >1800 28 28 100. 50 >18 T+ = union of the set of potentially positive – 55 – terms for each function

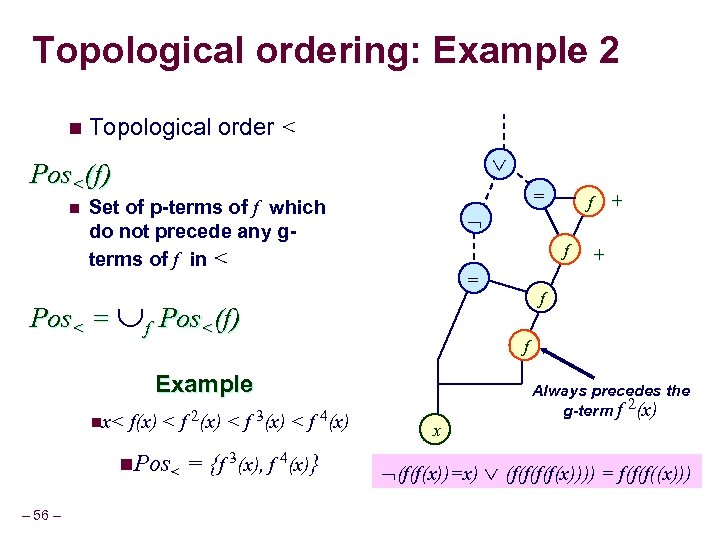Topological ordering: Example 2 n Topological order < Pos<(f) n = Set of p-terms of f which do not precede any gterms of f in < f = Pos< = f Pos<(f) f(x) < f 2(x) < f 3(x) < f 4(x) n. Pos< – 56 – = {f 3(x), f 4(x)} + f f Example nx< f + x Always precedes the g-term f 2(x) (f(f(x))=x) (f(f(x)))) = f(f(f((x)))

Finding the best topological ordering With multiple non-zero arity function symbol n Best order may not be best for each symbol = f Example 1. 3 topological orders on terms x

Relevant papers l “Exploiting positive equality in a logic of equality with uninterpreted functions” n Bryant, German and Velev, CAV’ 99 l “Revisiting Positive Equality” n n – 58 – Lahiri, Bryant, Goel and Talupur, TACAS’ 04 Generalization of positive equality

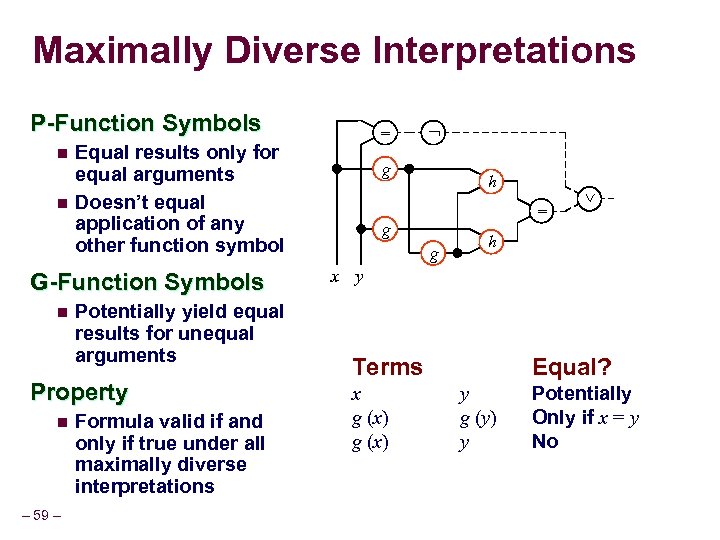Maximally Diverse Interpretations P-Function Symbols n n Equal results only for equal arguments Doesn’t equal application of any other function symbol G-Function Symbols n Potentially yield equal results for unequal arguments Property n – 59 – = Formula valid if and only if true under all maximally diverse interpretations g h = g g h x y Terms x g (x) Equal? y g (y) y Potentially Only if x = y No

Robust maximally diverse interpretations For every p-term h(T 1, …, Tn) n If args. do not equal the args. of any g-term h(U 1, …, Un), then l Can only equal other h application terms with equal arguments Property n – 60 – Formula valid if and only if true under all robust maximally diverse interpretations

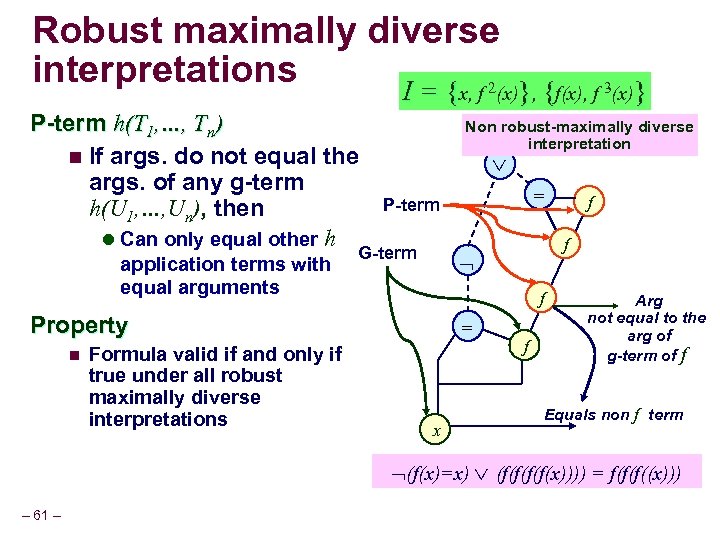Robust maximally diverse interpretations I = {x, f 2(x)}, {f(x), f 3(x)} P-term h(T 1, …, Tn) n If args. do not equal the args. of any g-term h(U 1, …, Un), then l Can only equal other h application terms with equal arguments Non robust-maximally diverse interpretation G-term f Formula valid if and only if true under all robust maximally diverse interpretations = x f f Property n = P-term f Arg not equal to the arg of g-term of f Equals non f term (f(x)=x) (f(f(x)))) = f(f(f((x))) – 61 –