ПАРНАЯ И МНОЖЕСТВЕННАЯ ЛИНЕЙНАЯ РЕГРЕССИЯ Лекция доктора физ

ПАРНАЯ И МНОЖЕСТВЕННАЯ ЛИНЕЙНАЯ РЕГРЕССИЯ Лекция доктора физ. -мат. наук, профессора ЩЕТИНИНОЙ Е. К.

В многофакторном регрессионном анализе в сравнении с парным регрессионным анализом возникают, как минимум, две новые проблемы: необходимо решить проблему спецификации (определить какие из переменных оказывают на показатель существенное влияние, какие нет); при анализе влияния конкретного фактора Xi на показатель Y следует отделить влияние на Y переменной от Xi влияния других факторных переменных.

Множественной линейной регрессией Y на X называется линейная стохастическая зависимость между показателем Y и фактором X (1) неизвестные параметры модели U характеризует влияние на показатель Y отличных от X факторов (остатки, отклонения) оценки параметров оценка модели (1)

Множественной линейной регрессией Y на называется линейная стохастическая зависимость между показателем Y и факторами (1) неизвестные параметры модели U характеризует влияние на показатель Y отличных от факторов (остатки, отклонения) оценки параметров оценка модели (1)

Методом наименьших квадратов (МНК), который разработали К. Гаусс , П. Лаплас , оценки параметров модели подбирают, минимизируя сумму квадратов отклонений фактических значений показателя от его расчетных значений. Система нормальных уравнений Гаусса

Матричная форма записи оценки модели (1) (2) Здесь введены переменные вектор-столбец фактических значений показателя матрица значений факторов

вектор-столбец оценок параметров модели вектор-столбец расчетных значений показателя

Методом наименьших квадратов находим значения компонент вектора оценок B (3) Для корректного применения МНК предполагается существование обратной матрицы

Важным этапом корреляционного анализа зависимостей является оценка практической значимости синтезированной модели, которую проводят при помощи показателей тесноты связи между и. Множественным коэффициентом кореляции называют парный коэффициент корреляции между фактическими и теоретическими значениями показателя. Чем ближе R к 1, тем точнее данная модель описывает исследуемый процесс.

Для парной линейной регрессии справедливо равенство

Коэффициент детерминации составляет одну из наиболее эффективных оценок адекватности регрессионной модели. Он является мерой качества модели и ее прогностической силы. Коэффициент детерминации указывает, какая часть дисперсии результативного показателя объясняется построенной регрессионной зависимостью.

Средняя ошибка аппроксимации определяет среднее относительное отклонение между фактическими и теоретическими уровнями показателями для построенной модели. Если средняя ошибка аппроксимации не превосходит 5%, то модель считают адекватной фактическим данным.

Для получения выводов о практической значимости модели показателям тесноты связи дают количественную оценку на основе шкалы Чеддока. 0, 8— 0, 9— 0, 99 Очень высокая Заметная 0, 7 --0, 8 Высокая 0, 6— 0, 7 Слабая Очень слабая Характери стика силы связи <0, 5 Средняя Величина показателя

Проверка значимости уравнения множественной регрессии проводится по критерию Фишера По таблицам критических точек Фишера находят уравнение регрессии является значимым, коэффициент множественной корреляции значимо отличается от нуля, между показателем и всеми факторами существует линейная корреляционна зависимость

Проверка значимости уравнения парной регрессии По таблицам критических точек Фишера находят уравнение регрессии является значимым, коэффициент множественной корреляции значимо отличается от нуля, между показателем и фактором существует линейная корреляционна зависимость

Проверка значимости параметра уравнения регрессии проводится по критерию Стьюдента диагональный элемент матрицы По таблицам критических точек Стьюдента находят параметр значимо отличается от нуля, между показателем и фактором существует линейная корреляционна зависимость. Проверка значимости параметра имеет второстепенное значение, поскольку постоянная регерссии чаще всего не имеет экономического смысла

Проверка значимости параметра уравнения парной регрессии проводится по критерию Стьюдента По таблицам критических точек Стьюдента находят параметр значимо отличается от нуля, между показателем и фактором существует линейная корреляционна зависимость Проверка значимости парной модели регрессии эквивалентна проверке значимости параметра регрессии.

Доверительный интервал для Парная регрессия Доверительный интервал для

Доверительный интервал для Парная регрессия Доверительный интервал для

Экономический смысл параметров регрессии Если фактор Xk изменится на единицу своего измерения при прочих равных условиях, то показатель Y изменится в среднем на bk единиц своего измерения. Параметр b 0 определяет уровень показателя Y при нулевом уровне объясняющих переменных (факторов). Интерпретация оценок параметров уравнения парной регрессии полностью аналогична.

Коэффициент эластичности показателя Y по фактору Xk является безразмерной величиной, определяющей влияние этого фактора на показатель Если фактор Xk изменится на 1%, то показатель Y изменится на Для линейной регрессии чаще всего коэффициент эластичности вычисляют для среднего Если фактор Xk изменится в среднем на 1%, то показатель Y изменится в среднем на

Прогнозирование Точечное Интервальный доверительный надежностью Y 0. прогноз представляет собой интервал, который с заданной покрывает ожидаемую величину

Пример. Директор по экономике отвечает за увеличение прибыли предприятия от торговых операций. Самым важным источником прибыли является прибыль от реализации произведенных товаров. Директор исследует этот показатель на основе десяти наблюдений в филиалах за изменением прибыли и другими переменными. Y – прибыль от реализации продукции предприятия, тыс. грн. X 1 – затраты на рекламу продукции, тыс. грн. X 2 – расходы на автотранспортный парк предприятия, тыс. грн. X 3 – объем производства, тыс. т

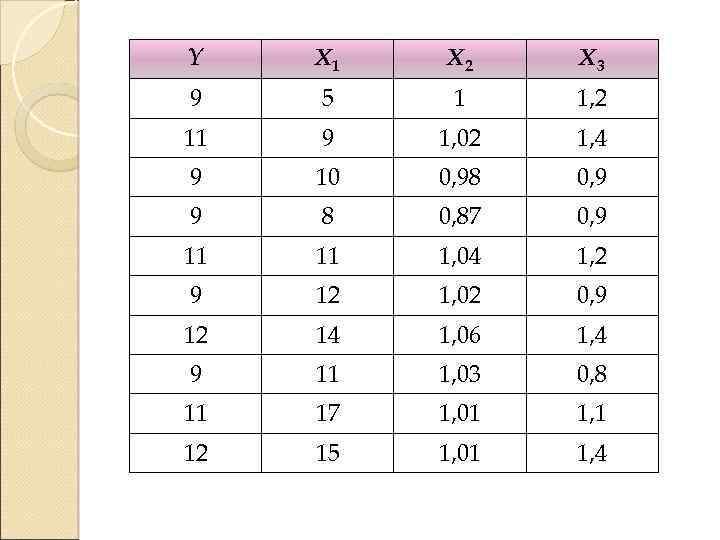Y X 1 X 2 X 3 9 5 1 1, 2 11 9 1, 02 1, 4 9 10 0, 98 0, 9 9 8 0, 87 0, 9 11 11 1, 04 1, 2 9 12 1, 02 0, 9 12 14 1, 06 1, 4 9 11 1, 03 0, 8 11 17 1, 01 1, 1 12 15 1, 01 1, 4

БЛАГОДАРЮ ЗА ВНИМАНИЕ ! ! !