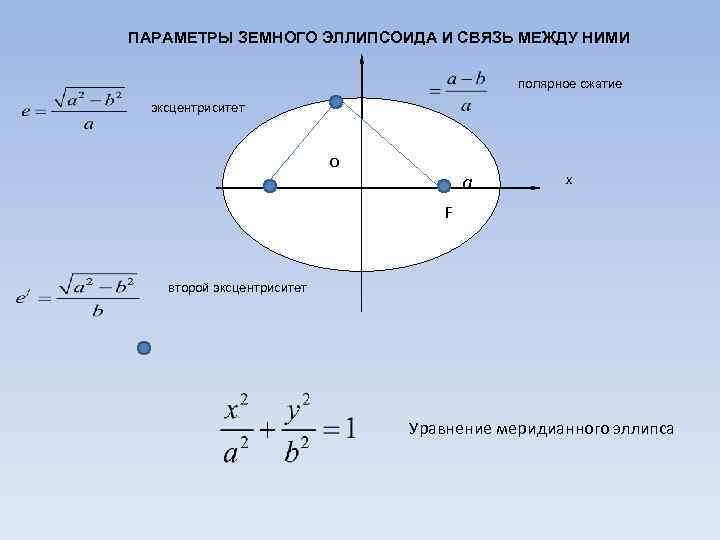
ПАРАМЕТРЫ ЗЕМНОГО ЭЛЛИПСОИДА И СВЯЗЬ МЕЖДУ НИМИ полярное

ПАРАМЕТРЫ ЗЕМНОГО ЭЛЛИПСОИДА И СВЯЗЬ МЕЖДУ НИМИ полярное сжатие эксцентриситет o a x F второй эксцентриситет Уравнение меридианного эллипса

несложно получить формулы связи различных параметров: ) = a =

СИСТЕМЫ КООРДИНАТ ВЫСШЕЙ ГЕОДЕЗИИ И СВЯЗЬ МЕЖДУ НИМИ Уравнение поверхности эллипсоида вращения в системе пространственных прямоугольных координат имеет вид

z (y) P G L Q O B n (x) Если в x = 0 или y = 0 получим уравнения меридианных эллипсов

z=0 получим уравнение геодезического экватора, который представляет собой окружность радиуса a

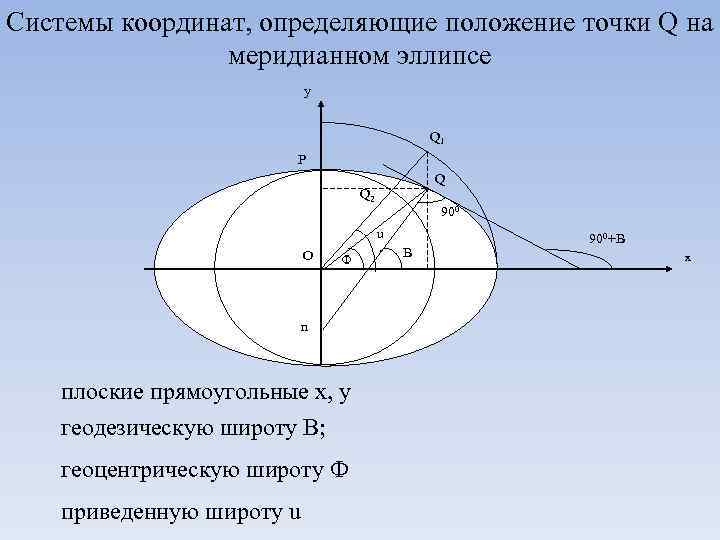Системы координат, определяющие положение точки Q на меридианном эллипсе y Q 1 P Q Q 2 900 u O Ф n плоские прямоугольные x, y геодезическую широту B; геоцентрическую широту Ф приведенную широту u B 900+B x

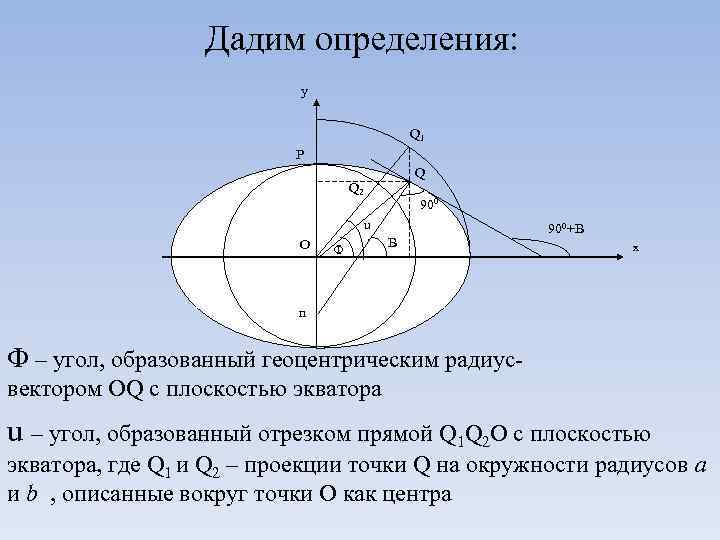Дадим определения: y Q 1 P Q Q 2 900 u O Ф B 900+B x n Ф – угол, образованный геоцентрическим радиусвектором OQ с плоскостью экватора u – угол, образованный отрезком прямой Q 1 Q 2 O с плоскостью экватора, где Q 1 и Q 2 – проекции точки Q на окружности радиусов a и b , описанные вокруг точки О как центра

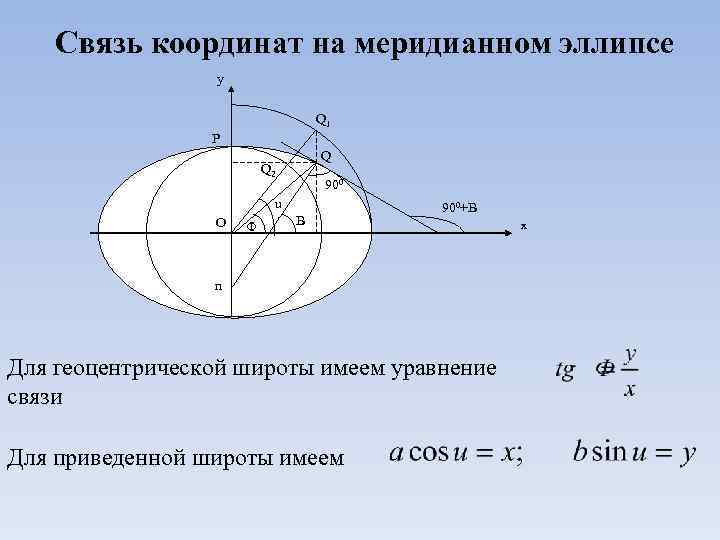Связь координат на меридианном эллипсе y Q 1 P Q Q 2 900 u O Ф B 900+B n Для геоцентрической широты имеем уравнение связи Для приведенной широты имеем x

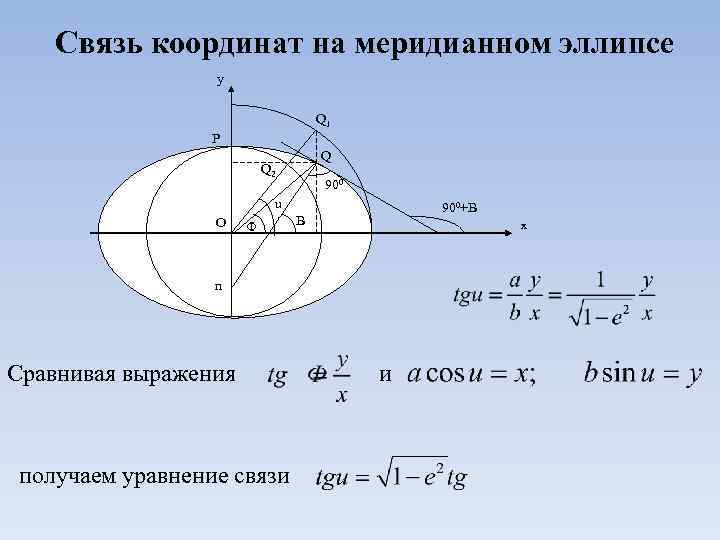Связь координат на меридианном эллипсе y Q 1 P Q Q 2 900 u O Ф 900+B B x n Сравнивая выражения получаем уравнение связи и

Связь координат на меридианном эллипсе y Q 1 P Q Q 2 900 u O Ф B 900+B n Применительно к данному рисунку можем записать x

Дифференцируем по переменной x уравнение меридианного эллипса Получим: откуда имеем для производной Приравнивая правые части уравнений

Учитывая выражения запишем следующие уравнения связи широт

Используя полученные уравнения имея в виду уравнения получаем выражения для плоских прямоугольных координат x, y в функции широт:

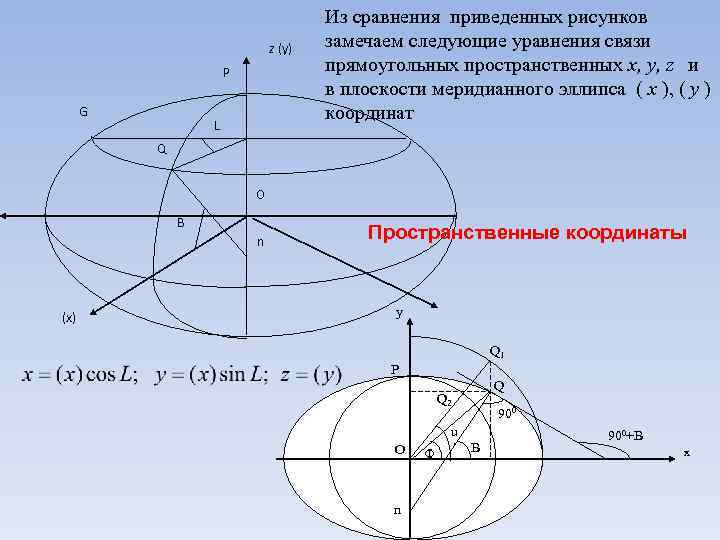z (y) P G L Из сравнения приведенных рисунков замечаем следующие уравнения связи прямоугольных пространственных x, y, z и в плоскости меридианного эллипса ( x ), ( y ) координат Q O B n (x) Пространственные координаты y Q 1 P Q Q 2 900 u O n Ф B 900+B x

Пространственные координаты Подставляя в выражения для ( x ) и ( y ) получим уравнения связи W называют первой основной функцией широты

Пространственные координаты Если точка Q не расположена на поверхности эллипсоида и характеризуется геодезической высотой Н, то уравнения связи пространственных прямоугольных и геодезических широт , долгот и высот принимают вид Радиус кривизны 1 вертикала (отрезок Qn) z (y) P G L Q O B (x) n

Пространственные координаты Возведя в квадрат уравнения для х и у системы и найдя их сумму получаем Полученное уравнение совместно с уравнением для z приводит к уравнению решается методом последовательных приближений

Пространственные координаты Для удобства вычислений формулу преобразовывают Путем замены в правой части В результате, получим Определив долготу и широту по приведенным формулам, геодезическую высоту можно определить