ПАРАМЕТРИЗАЦИЯ МОДЕЛИ ЛЕКЦИЯ План лекции

ПАРАМЕТРИЗАЦИЯ МОДЕЛИ ЛЕКЦИЯ

План лекции 1. Оценка параметров линейной регрессии, основанная на методе наименьших квадратов

Определение параметров экономико- статистической модели заключается в установлении числовых характеристик выбранной ранее математической зависимости. Для определения параметров РМ могут применяться различные методы: 1. Графический метод 2. Метод наименьших квадратов (МНК)

Определение параметров линейной РМ на примере линейной парной регрессии Y x = a 0 + a 1 * x или Y = a 0 + a 1 * x + Δ i Y – факт значение зависимой переменной; Y x – теоретическое значение, полученное из уравнения регрессии, при подстановке факт значений независимой переменной x; a 0, a 1 – параметры, коэф. уравнения; Δ i - с лучайная величина, характеризующая отклонение фактического значения зависимой переменной от теоретически найденного.

Применение МНК позволяет более точно находить параметры функции при помощи решения системы нормальных уравнений. После выбора уравнения, наиболее соответствующего корреляционной зависимости, необходимо определить числовые значения параметров уравнения а 0 и а 1.

Согласно МНК неизвестные параметры уравнения а 0 и а 1 считаются правильными, при которых сумма квадратов отклонений фактических данных ( Y i факт) от расчетных ( Y x расч ) , найденных по уравнению регрессии, является минимальной.

S = (Yi – Yxi )2 → Min Из всего множества линий на графике выбирается линия регрессии таким образом, чтобы сумма квадратов расстояний по вертикали между точками и этой линией была минимальной. Yi– Yxi = Δ i Следовательно, S = Δ i 2 → Min

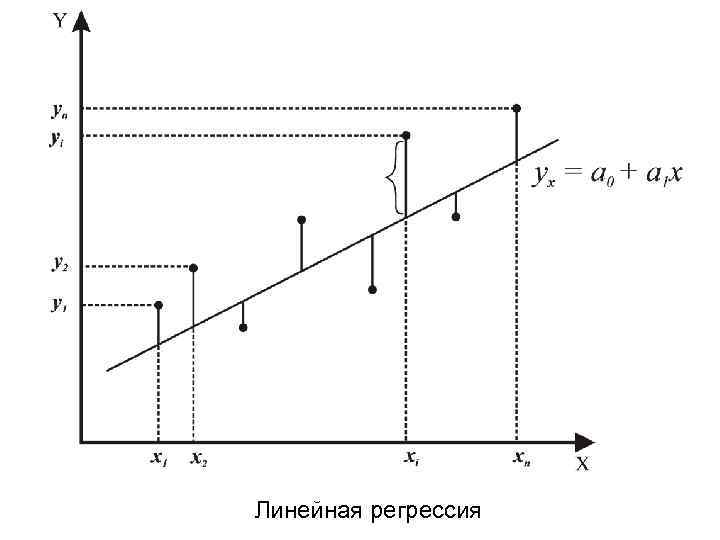Линейная регрессия

С целью найти минимум функции, надо вычислить частные производные по каждому из параметров a 0 a 1 и при равнять их к нулю. Тогда: S = Δi 2 = (Yi – Yxi )2 = (Yi – a 0 – a 1 x)2

l d. S / da 0 = 2 (Yi – a 0 – a 1 x) =0 Или Yi – na 0 – a 1 x = 0 d. S / da 1 = 2 (Yi – a 0 – a 1 x) x =0 Или x Y i – a 0 x – a 1 x 2 = 0

В результате преобразований получим систему нормальных уравнений. Для отыскания параметров уравнения регрессии необходимо решить следующие системы нормальных уравнений:

для парной линейной зависимости

для параболы

Для множественной линейной зависимости

Для гиперболической зависимости

Решая систему нормальных уравнений методом подстановки, последовательного исключения переменных либо методом определителей, найдем искомые оценки параметров a 0 и a 1.