ПАРАМЕТРИЗАЦИЯ КОТОРОТКОВОЛНОВОЙ РАДИАЦИИ НА ПОВЕРХНОСТИ МОРЯ Массовые наблюдения

ПАРАМЕТРИЗАЦИЯ КОТОРОТКОВОЛНОВОЙ РАДИАЦИИ НА ПОВЕРХНОСТИ МОРЯ Массовые наблюдения коротковолновой радиации в морских условиях практически отсутствуют, так как попутные суда не экипированы пиранометрами и пиргеометрами. Таким образом, инсоляция должна быть рассчитана из местоположения судна, времени суток и информации об облачности, оцениваемой визуально моряками. Такие оценки - относительно грубые, однако они представляют основу наших знаний о коротковолновой радиации на сегодня.

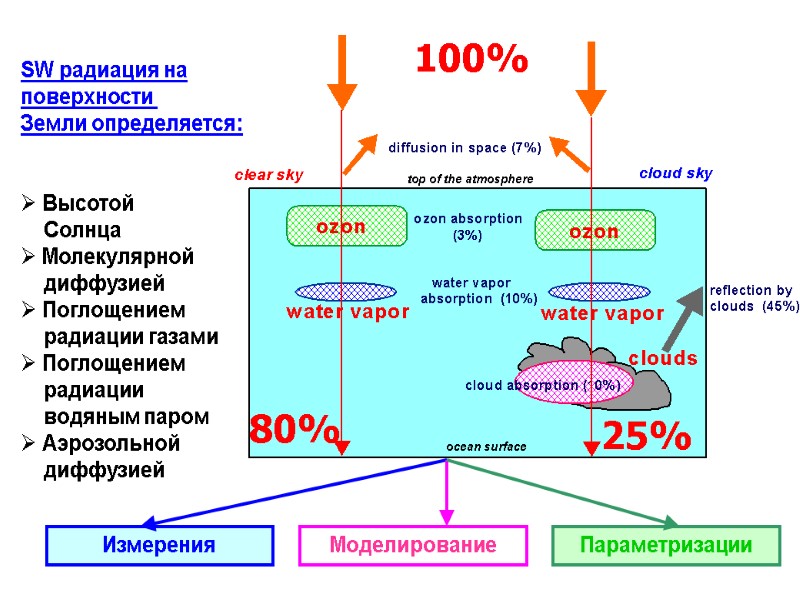
SW радиация на поверхности Земли определяется: Высотой Солнца Молекулярной диффузией Поглощением радиации газами Поглощением радиации водяным паром Аэрозольной диффузией Измерения Моделирование Параметризации

Поток коротковолновой радиации (SW) может быть параметризован (т.е. выражен в терминах параметров измеряемых in-situ) как: Qsw = Qt TF (1) где Qt =S0 cos h (2) Qt - коротковолновая радиация на верхней границе атмосферы, S0 - Соленчная постоянная, h - высота Солнца, TF - фактор пропускания атмосферы, который должен параметризоваться в терминах облачности и термодинамических параметров атмосферы. Что мы действительно измеряем у поверхности моря? SST,°C Ta,°C q, g/kg C (Cn, Cl), okta

Два подхода к параметризации коротковолновой радиации Одношаговые параметризации: фактор пропускания зависит от облачности и термодинамических характеристик атмосферы Двухшаговые параметризации: атмосферное пропускание разделяется на модификацию радиации чистым небом и эффект облачности

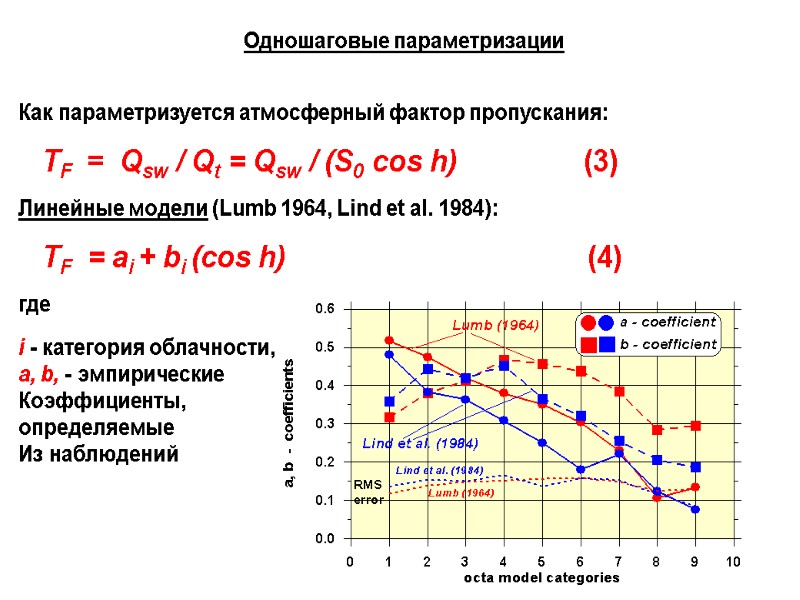
Одношаговые параметризации Как параметризуется атмосферный фактор пропускания: TF = Qsw / Qt = Qsw / (S0 cos h) (3) Линейные модели (Lumb 1964, Lind et al. 1984): TF = ai + bi (cos h) (4) где i - категория облачности, a, b, - эмпирические Коэффициенты, определяемые Из наблюдений

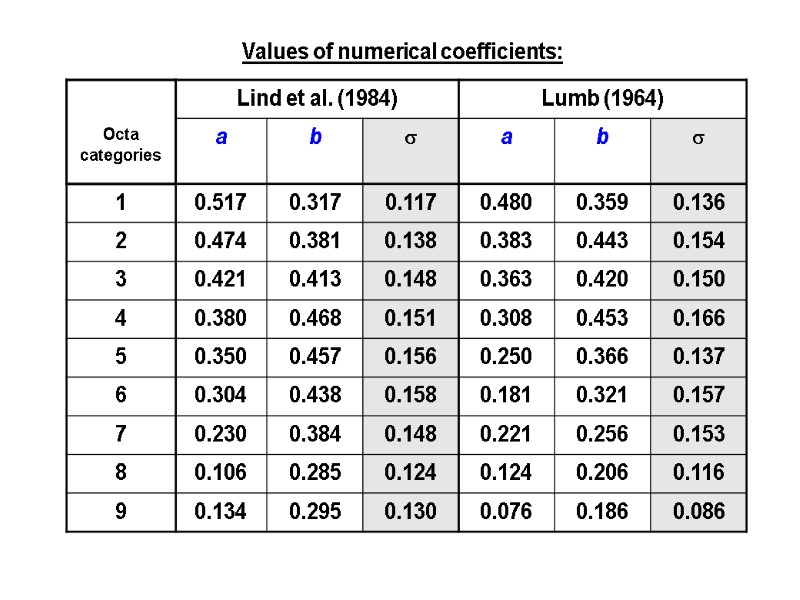
Values of numerical coefficients:

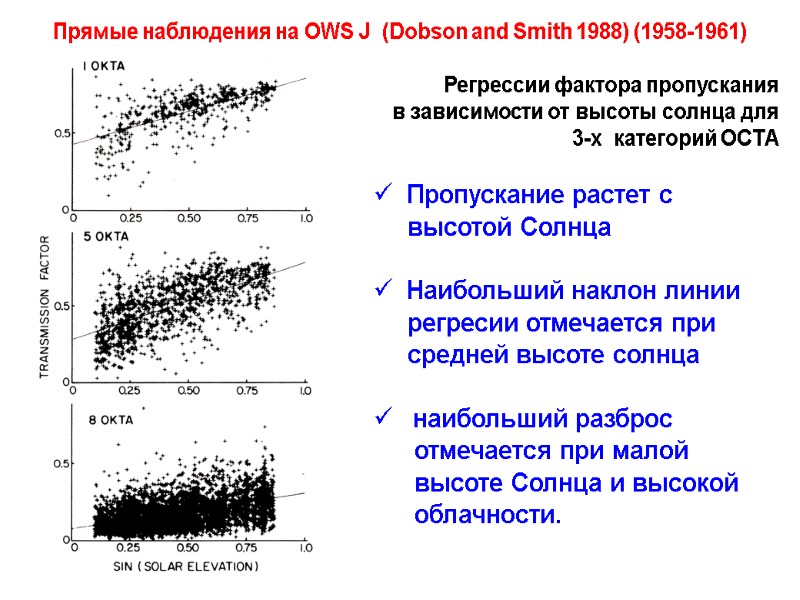
Прямые наблюдения на OWS J (Dobson and Smith 1988) (1958-1961) Регрессии фактора пропускания в зависимости от высоты солнца для 3-х категорий OCTA Пропускание растет с высотой Солнца Наибольший наклон линии регресии отмечается при средней высоте солнца наибольший разброс отмечается при малой высоте Солнца и высокой облачности.

Нелинейные модели: Экспериментальный анализ атмосферного фактора пропускания (Paltridge and Platt 1976, Dobson and Smith 1988): TF = F exp(-D0 /(cos h)) {C[exp(-Di /(cos h))+Ei ]+(1-C)} F приходящей радиации чистого неба, которая не поглощена атмосферными примесями D0 оптическая плотность чистого неба i категория облачности Di оптическая плотность облаков Ei фактор пропускания диффузной радиации через облака (1-C) доля неба, не покрытая облаками

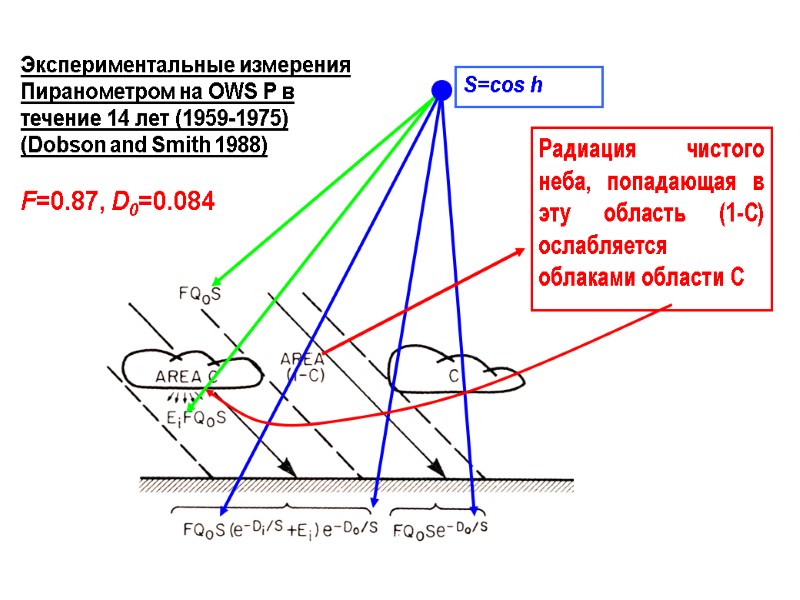
Экспериментальные измерения Пиранометром на OWS P в течение 14 лет (1959-1975) (Dobson and Smith 1988) F=0.87, D0=0.084

Резюме одношаговых параметризаций: Точность подхода назка, так как требуется рассмотрение радиационного переноса во всем столбе атмосферы Большинство параметров плохо определены, так как зависимость ослабления от измеряемых у поверхности величин крайне неопределенная Улучшение возможно, но требует знания трудно и редко измеряемых метеорологических параметров (типы облаков, код погоды) Рекомендации: Старайтесь избегать использования одношаговых параметризаций Никогда (!!) не используйте их в атмосферных моделях, даже если ваша модель радиационного переноса (RTM) в МОЦ плохо работает Если Вы, тем не менеее решили ее использовать, возьмите нелинейную схему Dobson and Smith (1988) с коэффициентами, полученными at Sable Island

Двухшаговые параметризации Чтобы уменьшить неопределенности, целесообразно разделить фактор атмосфрерной модификации коротковолновой радиации на два члена: Модификация коротковолновой радиации в условиях чистого неба (астрономия, температура, влажность, аэрозоли). Модификация радиации облачностью. В этом случае общая формула для SW радиации: Qsw = Q0 F(n, T, q, h) (4) Q0 радиация чистого неба на поверхности моря, являющаяся функцией асторономии и радиационного пропускания атмосферы чистого неба. F(n, T, q, h) эмпирическая функция балла облачности n, температуры воздуха T, влажности воздуха q, и высоты Солнца h Что надо параметризовать? Q0 и F(n, T, q, h)

1. Радиация чистого неба В большинстве схем она параметризуется через чисто астрономические параметры (широта и высота Солнца) и и эмпирические коэффициенты, учитывающие прозрачность атмосферного воздуха в остутствии облаков (e.g. Seckel and Beaudry 1973): Smithsonian formula Q0 = A0+A1cos+B1sin+A2cos2+B2sin2 (5)  = (t-21)(360/365), t время в днях года, L долгота Lat: 20S – 40N A0=-15.82+326.87cosL A1=9.63+192.44cos(L+90) B1=-3.27+108.70sinL A2=-0.64+7.80sin2(L-45) B2=-0.50+14.42cos2(L-5) Lat: 40N – 60N A0=342.61-1.97L-0.018L2 A1=52.08-5.86L+0.043L2 B1=-4.80+2.46L-0.017L2 A2=1.08-0.47L+0.011L2 B2=-38.79+2.43L-0.034L2

Smithsonian-формула – только для месячных значений! Для оценок часовых сумм солнечной радиации надо использовать формулу Lumb (1964): Q0 = 1353 (sin h) [0.61+0.20 (sin h)] Будьте осторожны !!! – всегда учитывайте, работаете Вы с месячными или суточными значениями

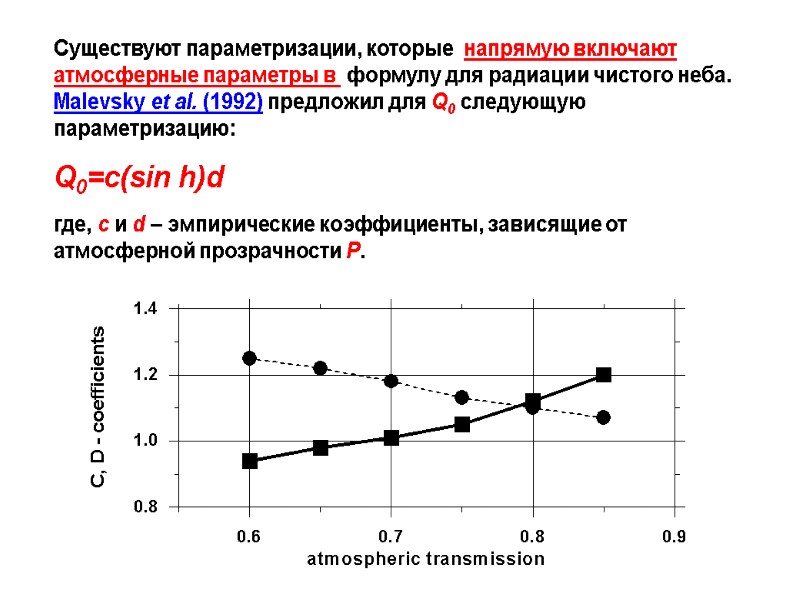
Существуют параметризации, которые напрямую включают атмосферные параметры в формулу для радиации чистого неба. Malevsky et al. (1992) предложил для Q0 следующую параметризацию: Q0=c(sin h)d где, c и d – эмпирические коэффициенты, зависящие от атмосферной прозрачности P.

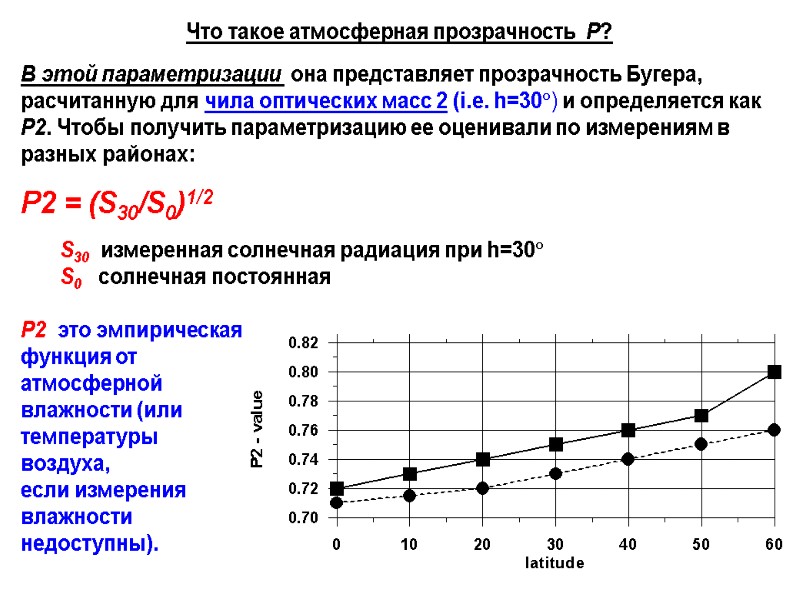
Что такое атмосферная прозрачность P? В этой параметризации она представляет прозрачность Бугера, расчитанную для чила оптических масс 2 (i.e. h=30) и определяется как P2. Чтобы получить параметризацию ее оценивали по измерениям в разных районах: P2 = (S30/S0)1/2 S30 измеренная солнечная радиация при h=30 S0 солнечная постоянная P2 это эмпирическая функция от атмосферной влажности (или температуры воздуха, если измерения влажности недоступны).

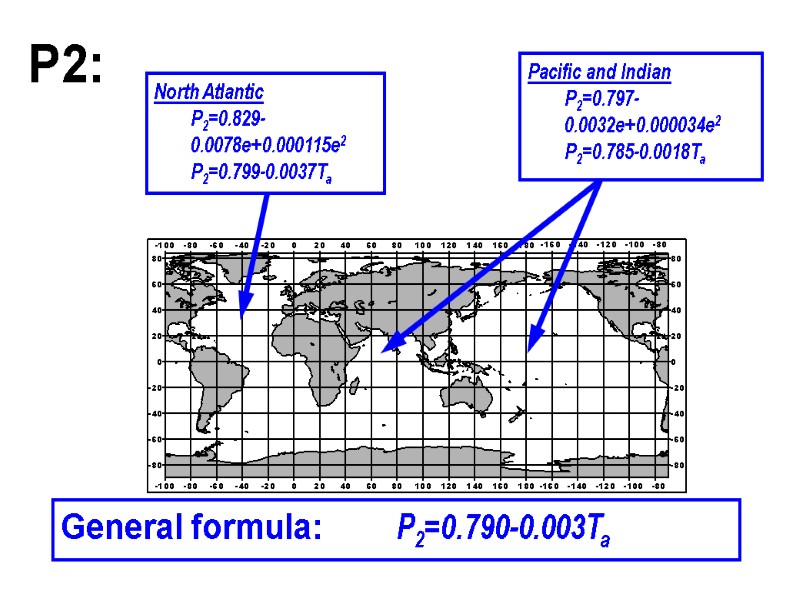
North Atlantic P2=0.829-0.0078e+0.000115e2 P2=0.799-0.0037Ta Pacific and Indian P2=0.797-0.0032e+0.000034e2 P2=0.785-0.0018Ta General formula: P2=0.790-0.003Ta P2:

2. Фактор ослабления радиации облаками ЧТО ЭТО ТАКОЕ? Это компромис между сложной физикой радиационного перноса в облачной атмосфере и доступностью данных, чтобы описать эту сложность. Очевидно, что наиболее физически обоснованное описание можно построить только на основе учета типов облаков и их высоты (e.g. Dobson and Smith 1988). Однако, единственным массовым и более-менее достоверно определяемым параметром является общая облачность.

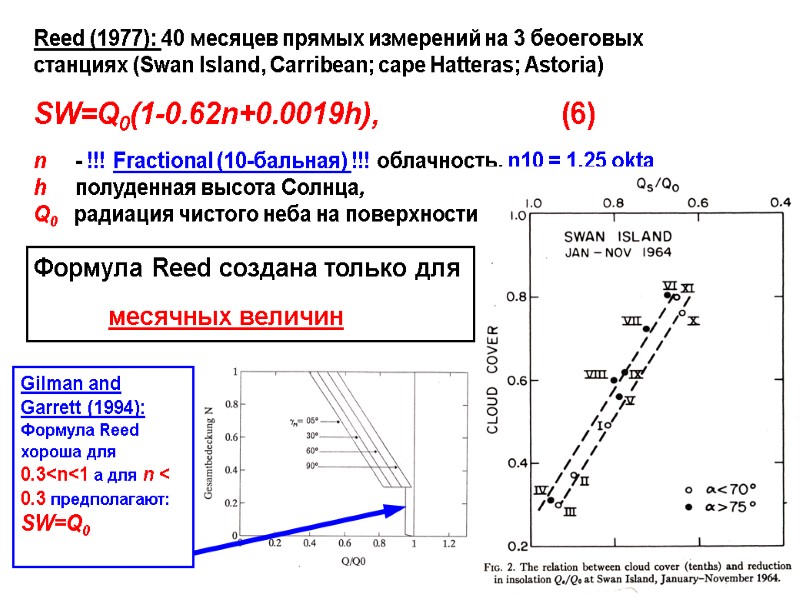
Reed (1977): 40 месяцев прямых измерений на 3 беоеговых станциях (Swan Island, Carribean; cape Hatteras; Astoria) SW=Q0(1-0.62n+0.0019h), (6) n - !!! Fractional (10-бальная) !!! облачность, n10 = 1.25 okta h полуденная высота Солнца, Q0 радиация чистого неба на поверхности Gilman and Garrett (1994): Формула Reed хороша для 0.3

Malevsky et al. (1992) предложил схему для совместного использования общей и нижней облачности что тоже доступно из наблюдений попутных судов. Эта параметризация основана на более чем 19000 наблюдений в разных широтных районах. Для общего балла облачности and средних океанских условий: SW=Q0(1+0.19nt-0.71nt), (7) nt - !!! Fractional (10-бальная) !!! общая облачность Эта схема учитывает вторичное отражение радиации от кромок облаков при малых углах наклона Солнца и малой облачности, что допускает, что “облачный” коэффициент становится больше 1. Эта формула дает общую зависимость и ее не стоит в виде (7) использовать в практике расчетов. Для практических расчетов (общая облачность и двух-слойная облачность) величины затабулированы (см программу). Параметризация Малевского используется для часовых сумм

Резюме двух-шаговых параметризаций: Большинство из них основано на наблюдениях в средних широтах. Тропическая облачность имеет несколько другие характеритики прозрачности. Сообщество специалистов в области атмосферной радиации избегают формул (6, 7), т.к. они предполагают постоянную оптическую плотность. В нормальной (RTM) возмущения поверхностной радиации индуцируются напрямую облачностью (n =1 in (6,7)). По той же причине спутниковые наблюдения радиации и облачности, равно как и оптической плотности облаков крайне важны. Тем не менее, формулы (6,7) будут использоваться еще очень долго.

Альбедо на поверхности моря Не вся солнечная радиация, приходящая на поверхность, усваивается оканом. Часть ее отражается от водной поверхности. Qsw=Qsw (1-A) A=Qsw / Qsw Теоретически альбедо определяется законом Френеля для полного внутреннего зеркального отражения: Три причины не использовать напрямую закон Френеля: Переменная прозрачность воды Шероховатость воды Влияние дифузивной кортоковолновой радиации ЧТО ДЕЛАТЬ?

Измерения и параметризация Широкополосное альбедо измеряется парой пиранометров, один из которых направлен вверх, а другой вниз, при этом, чтобы исключить влияние восходящей длиноволновой радиации нижний должен быть защищен. Это создает очевидные трудности Для судов в открытом океане. Более частыми являются наблюдения на платформах. Payne (1972) произвел наиболее уникальные измерения с платформы in Buzzards Bay, MA (41°N), и представил результаты, в терминах только двух параметров solar altitude и atmospheric transmittance. Последняя – отношение солнечной радиации фактически измеренной на поверхности радиции на верхней границе, определяемой солнечной постоянной, временем года и суток и широтой (Paltridge and Platt 1976).

Solar transmittance is affected by absorption or scattering from atmospheric constituents, mainly water vapor, ozone, aerosols and clouds. Thus, Payne’s (1972) parameterization actually relates to the varying ratio of diffusive to direct shortwave radiation. The Frenel laws predict (and common observation confirms) that reflectivity at a water surface increases toward glancing angles of incidence. For high solar altitude and clear skies the albedo is small, but any increases in the diffuse component due to cloudiness will reduce the average angle of incidence and increase the albedo. For low solar altitude, the addition of cloudiness has the opposite effect.

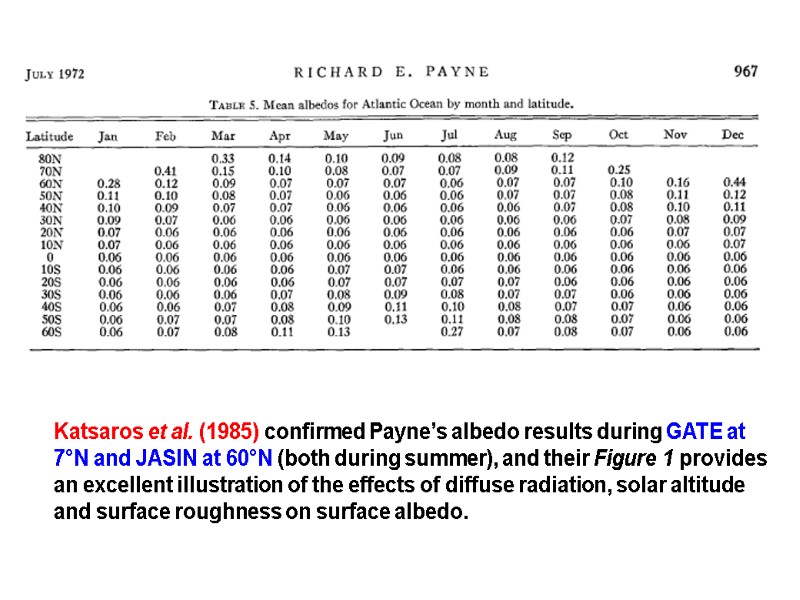
Katsaros et al. (1985) confirmed Payne’s albedo results during GATE at 7°N and JASIN at 60°N (both during summer), and their Figure 1 provides an excellent illustration of the effects of diffuse radiation, solar altitude and surface roughness on surface albedo.

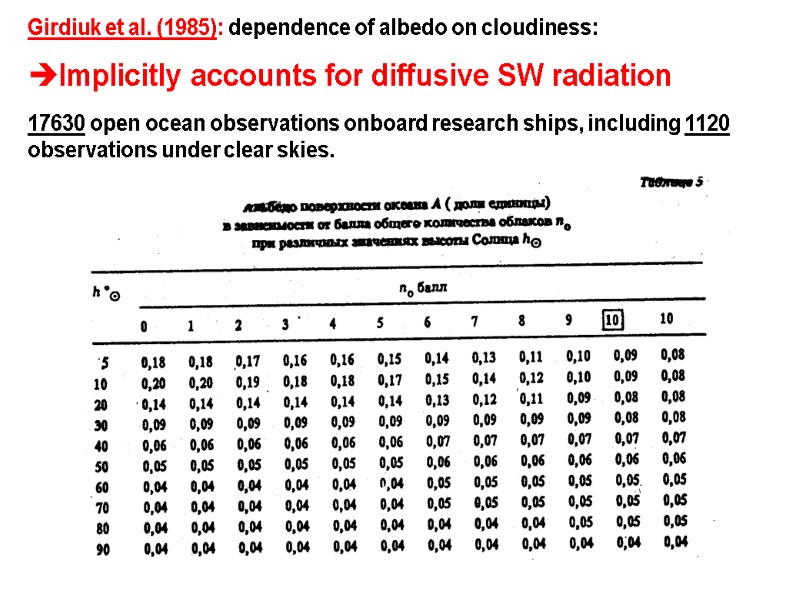
Girdiuk et al. (1985): dependence of albedo on cloudiness: Implicitly accounts for diffusive SW radiation 17630 open ocean observations onboard research ships, including 1120 observations under clear skies.

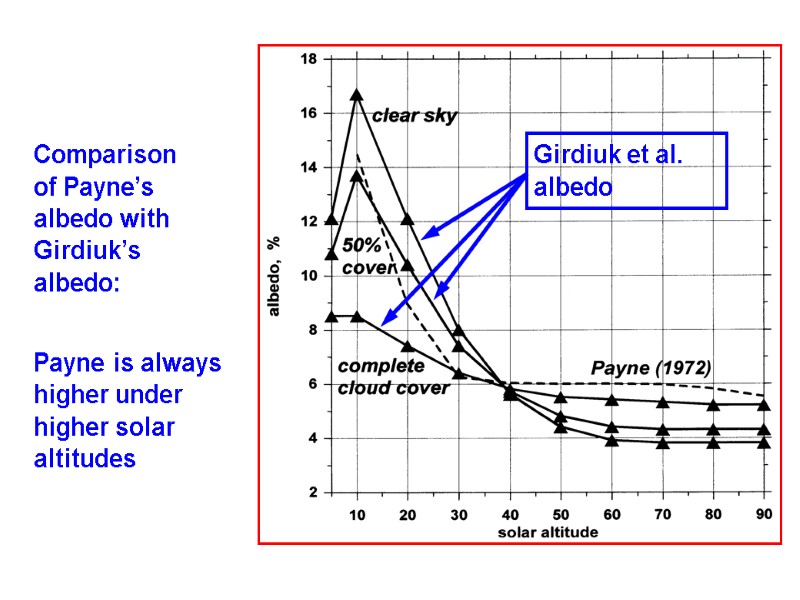
Comparison of Payne’s albedo with Girdiuk’s albedo: Payne is always higher under higher solar altitudes

MORE – Meridional oceanic radiative experiment IFM-GEOMAR / IORAS, A. Macke / S. Gulev Try to become part of MORE Contact: Prof. Andreas Macke: 600-4057, [email protected]

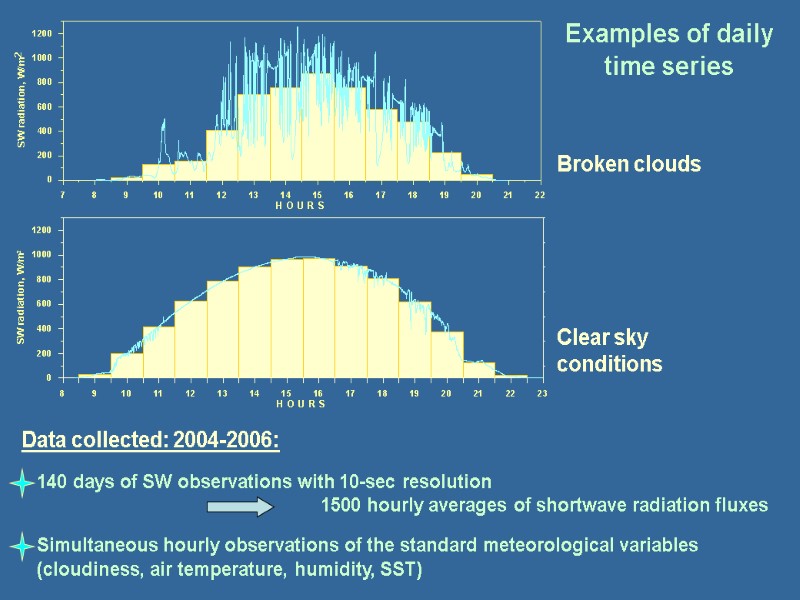
Data collected: 2004-2006: 140 days of SW observations with 10-sec resolution 1500 hourly averages of shortwave radiation fluxes Simultaneous hourly observations of the standard meteorological variables (cloudiness, air temperature, humidity, SST) Examples of daily time series Broken clouds Clear sky conditions

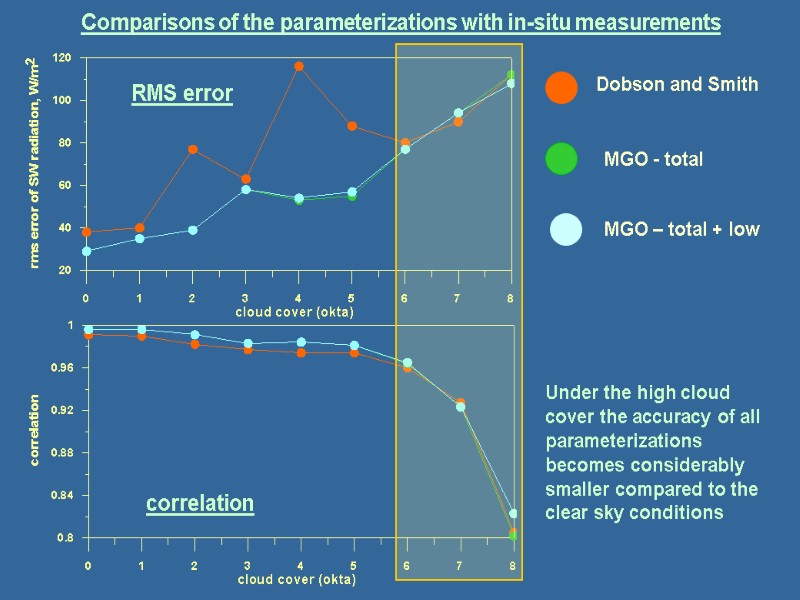
Comparisons of the parameterizations with in-situ measurements RMS error correlation Dobson and Smith MGO - total MGO – total + low Under the high cloud cover the accuracy of all parameterizations becomes considerably smaller compared to the clear sky conditions

The largest uncertainty is observed under the overcast conditions For the further improvement of parameterization we analyzed the dependency of atmospheric transmission on the cloud types and the state of the Sun disk. ☼2 ☼1 ☼0 ☼cloudy State of the Sun disk Different cloud types 8 octa - Ns 8 octa - Ns

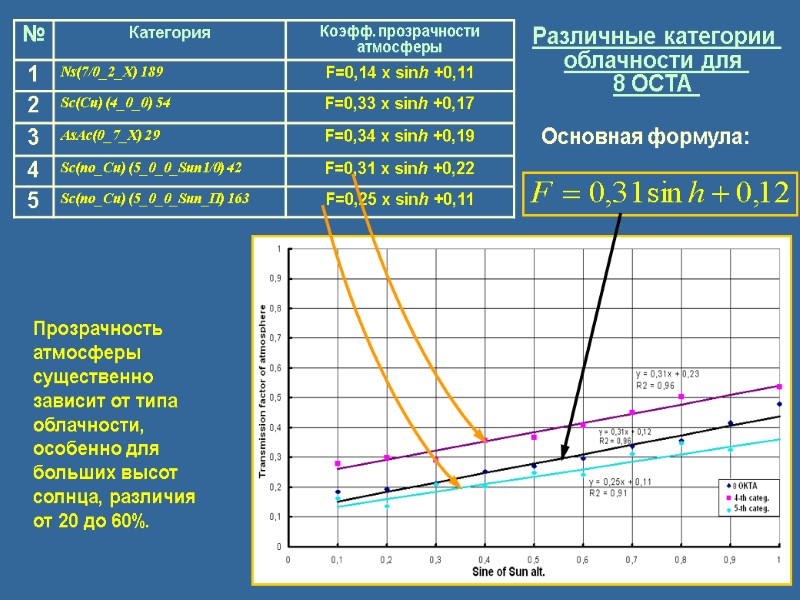
Различные категории облачности для 8 OCTA Основная формула: Прозрачность атмосферы существенно зависит от типа облачности, особенно для больших высот солнца, различия от 20 до 60%.

/helios/u2/gulev/handout/ radiation.f – collection of SW radiation F77 codes RSWM – Malevsky scheme for monthly means RSW – Malevsky scheme for individual values RSWD – Dobson and Smith scheme radiation1.f – another collection of SW radiation F77 codes (German comments!!!!) RSWISI – Reed’s scheme for monthly means Try to compare Malevsky, Dobson and Reed’s schemes: Clear sky, dependence on solar altitude Cloud cover octa=4, dependence on solar altitude h=10, h=30, h=60, dependence on cloud cover (in oktas)

READING Dobson, F., and S. D. Smith,1988: Bulk model of solar radiation at sea. Q.J.R.Meterol.Soc., 114,165-182. Girdiuk, G.V., T.V.Kirillova, and S.P.Malevsky, 1985: Cloudiness influence on the oceanic albedo. Meterol. Hydrol., 12, 63-69. Gulev, S.K., 1995: Long-term variability of sea-air heat transfer in the North Atlantic Ocean. Int.J.Climatol., 15, 825-852. Lumb, F.E., 1964: The influence of cloud on hourly amount of total solar radiation at the sea surface. Quart. J. Roy. Meteor. Soc., 90, 43-56. Malevsky, S.P., G.V.Girdiuk, and B.Egorov, 1992b: Radiation balance of the ocean surface. Hydrometeoizdat, Leningrad, 148 pp. Niekamp, K., 1992: Untersuchung zur Gute der Parametrizierung von Malevsky-Malevich zur Bestimmung der solaren Einsrahlung an der Oceanoberflache. Diploma MSc, Institut fuer Meereskunde, Kiel, 108 pp. Payne, R.E., 1972: Albedo at the sea surface. J.Atmos.Sci., 29, 959-970. Reed, R.K., 1977: On estimating insolation over the ocean. J.Phys.Oceanogr. 7, 482-485. Seckel, G.R., and F.H.Beaudry, 1973: The radiation from sun and sky over the Pacific Ocean (Abstratct) Trans. Am. Geophys. Union, 54, 1114.