Параметрический дискриминантый анализ в случае нормальных классов 1

Параметрический дискриминантый анализ в случае нормальных классов 1

Параметрический дискриминантый анализ в случае нормальных классов Пусть l-й класс описывается k-мерным нормальным законом распределения с вектором математических ожиданий и ковариационной матрицей (общей для всех p-классов ). Оценки параметров распределения находятся по обучающим выборкам объемом nl: где - значение j–го показателя для i-го наблюдения l–й выборки. 2

- оценка коэффициента ковариации между xj и xq - ми переменными, полученная по суммарной выборке объемом n. 3

Оценка плотности распределения l-й совокупности имеет вид: где - вектор-столбец текущих переменных; - несмещенная оценка ковариационной матрицы; - определитель ковариационной матрицы; - вектор средних значений переменных для l-ой обучающей выборки. 4

Правило классификации: Наблюдение относится к классу l 0 тогда и только тогда 5

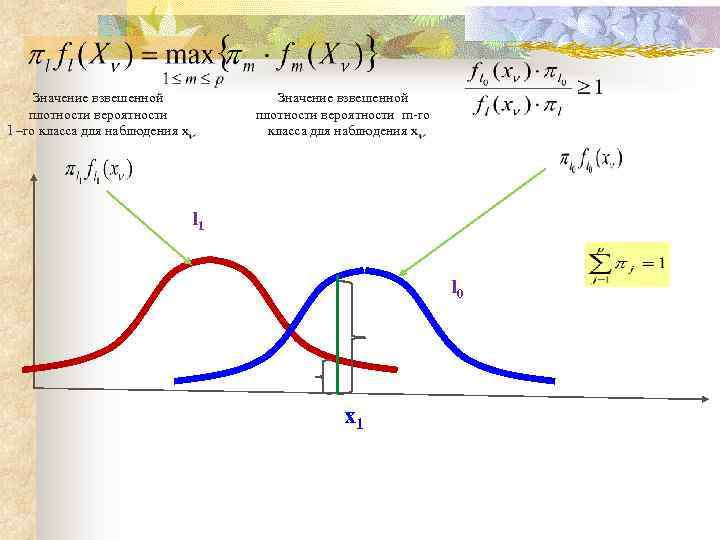Значение взвешенной плотности вероятности l –го класса для наблюдения x Значение взвешенной плотности вероятности m-го класса для наблюдения x l 1 l 0 x 1

Рассмотрим случай: p=2, Пусть из рассматриваемых нормальных генеральных совокупностей X и Y взяты две выборки объемом n 1 и n 2, по данным которых получены оценки параметров распределения: и пусть - значения показателя наблюдения, подлежащего классификации. . 7

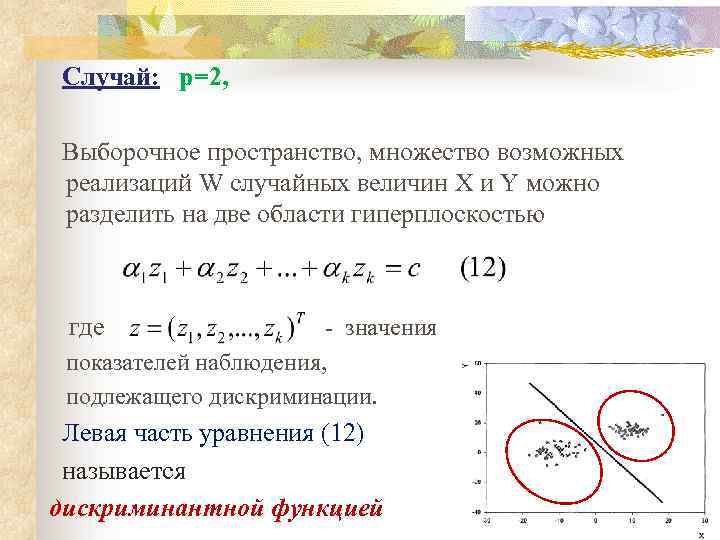Случай: p=2, Выборочное пространство, множество возможных реализаций W случайных величин X и Y можно разделить на две области гиперплоскостью где - значения показателей наблюдения, подлежащего дискриминации. Левая часть уравнения (12) называется дискриминантной функцией 8

Дискриминантная функция может быть представлена в виде и позволяет перейти от к-мерного пространства к одномерному. - вектор коэффициентов дискриминантной функции. 9

Таким образом, две подобласти пространства можно задать неравенствами: Если имеется элемент выборки то его относим к X, при и к Y при Таким образом, задача дискриминации сводится к определению коэффициентов дискриминантной функции и константы с. , 10

Алгоритм классификации n n v v Предположим, что известны априорные вероятности известно, что наблюдаемый объект принадлежит к первой X или второй Y генеральной совокупности. Также известны ущербы от ошибочной классификации: C(Y/X) – потери от ошибочного отнесения вектора наблюдения Z 0, принадлежащего совокупности (X), к совокупности (Y), а также C(X/Y) – потери от ошибочного отнесения Z 0 к X вместо Y. 11

Алгоритм классификации Предполагается также, что неизвестны параметры генеральной совокупности При таких условиях задача дискриминации решается с помощью, так называемой, обобщенной байесовской процедуры классификации. 12

n n Сначала по обучающим выборкам n 1 и n 2 находят оценки параметров генеральных совокупностей X и Y, вектор средних и оценку ковариационной матрицы - несмещенные оценки ковариационных матриц 13

n n В этом случае вектор оценок коэффициентов дискриминантной функции можно получить по формуле: оценка дискриминантной функции: (16) 14

Воспользовавшись оценкой дискриминантной функции получим n 1 значение этой функции для первой выборки Х n среднее значение из (17) и (18) следует, что 15

Аналогично для второй выборки Y получим: и 16

Константа оценивается выражением если принять, что Тогда, если а если , то Z 0 относится к X, , то Z 0 относится к Y. 17

Процедура дискриминации для случая р>2 Рассмотрим процедуру дискриминации для случая р>2 нормально распределенных генеральных совокупностей с параметрами , где l=1, 2, …, p. Согласно (10) оценку плотности fl(x) совокупности можно представить как: где – несмещенная оценка ковариационной матрицы , полученная по р - выборкам:

Процедура дискриминации для случая р>2 где – оценка ковариационной матрицы, полученная по l-ой выборке. Элемент матрицы определяется по формуле (9). - вектор-столбец текущих переменных; - вектор средних значений, полученных по l-ой обучающей выборке.

Предположив, что логарифм отношения правдоподобия (11) можно представить в виде Преобразуем левую часть неравенства 2 1 1 2

Преобразовав выражение, стоящее в квадратных скобках, получим: получено из 1 получено из 2

После преобразования окончательно получим:

Правило дискриминации: если для всех , где m=1, 2, …, р выполняется неравенство , то наблюдение X относится к l-ой совокупности ( ). В случае, когда: если для всех неравенство , , где m=1, 2, …, р выполняется то наблюдение X относится к l-ой совокупности.

Приведенное правило эквивалентно критерию: Наблюдение, определяемое вектором X, следует отнести к той совокупности X(l), расстояние Махаланобиса до центра которой минимально: а, следовательно, согласно (20) апостериорная плотность максимальна.

Спасибо за внимание! 25

После преобразования окончательно получим: и окончательно