Parameters to Control the Droplet Size Di Vi

Parameters to Control the Droplet Size. Di Vi Do m, s Orifice Disk Solid Surface Df Variables Reynolds Number (Re = Vi Do / n) Weber Number (We =r Vi 2 Do / s) Contact Angel (b) D = Df/Do Vf/Vi = Vi t / D o

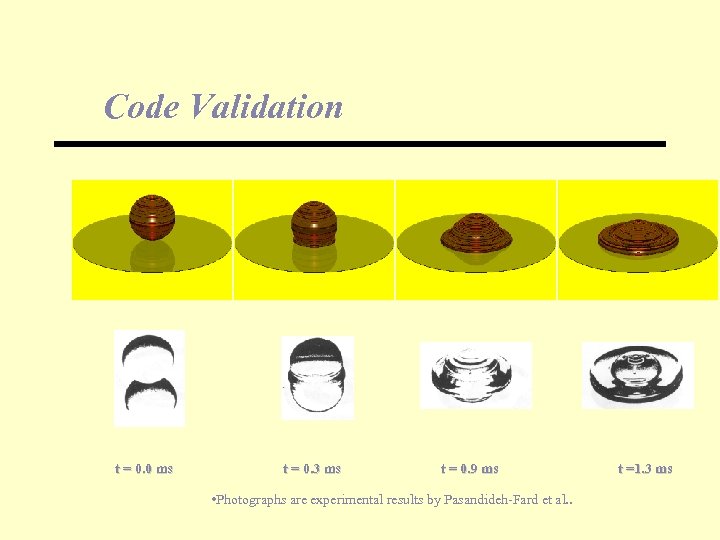Code Validation t = 0. 0 ms t = 0. 3 ms t = 0. 9 ms • Photographs are experimental results by Pasandideh-Fard et al. . t =1. 3 ms

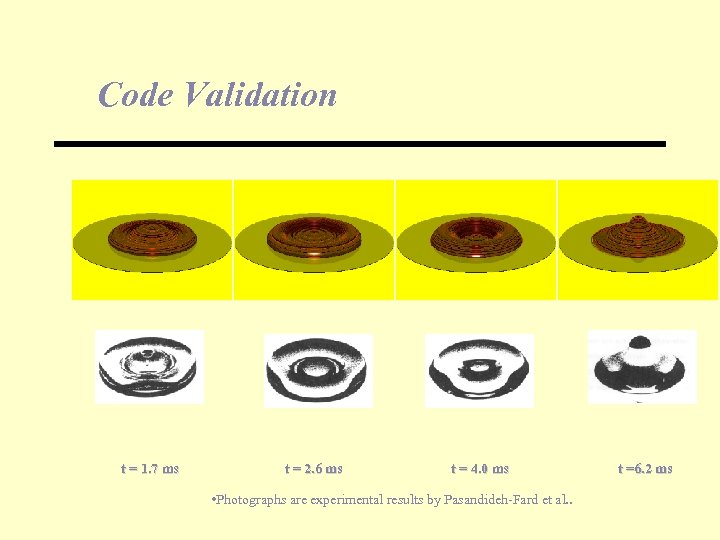Code Validation t = 1. 7 ms t = 2. 6 ms t = 4. 0 ms • Photographs are experimental results by Pasandideh-Fard et al. . t =6. 2 ms

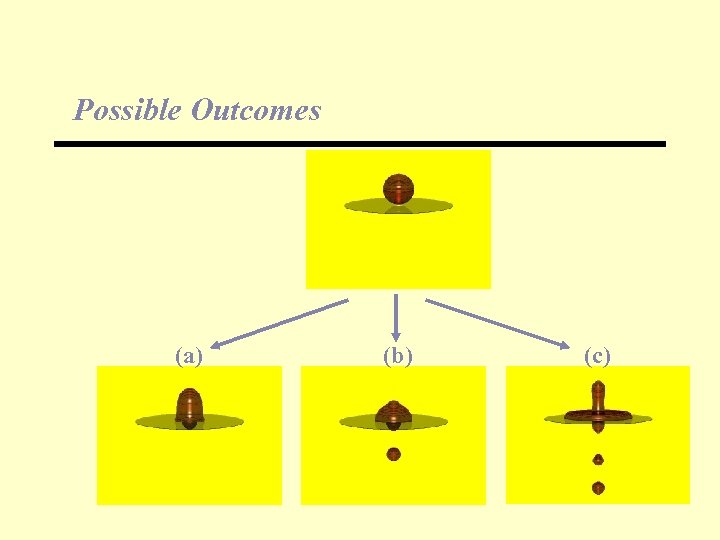Possible Outcomes (a) (b) (c)

Possible Outcomes: 1 - No Drops Re=240, We= 7. 2 Di=2 mm Do=0. 5 mm b=900

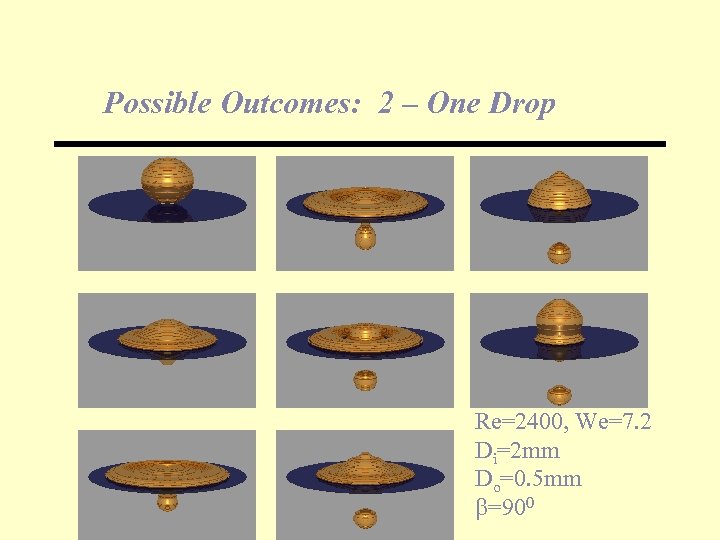Possible Outcomes: 2 – One Drop Re=2400, We=7. 2 Di=2 mm Do=0. 5 mm b=900

Possible Outcomes: 3 – Two Drops Re=600, We=14. 4 Di=2 mm Do=0. 5 mm b=900

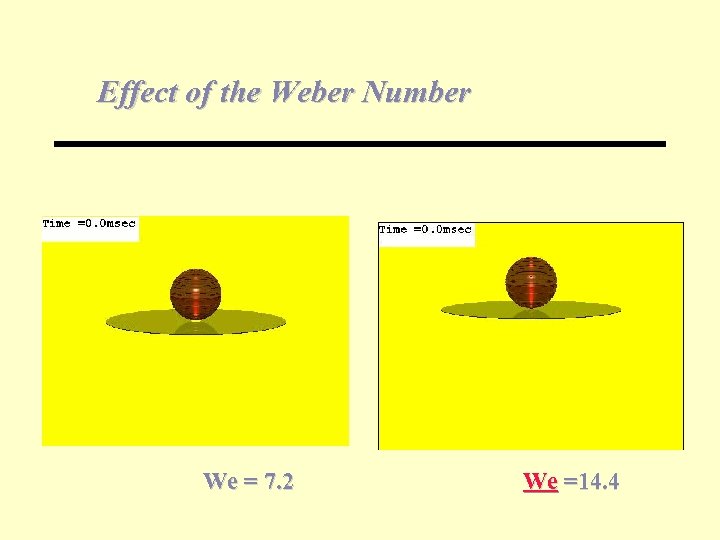Effect of the Weber Number We = 7. 2 We =14. 4

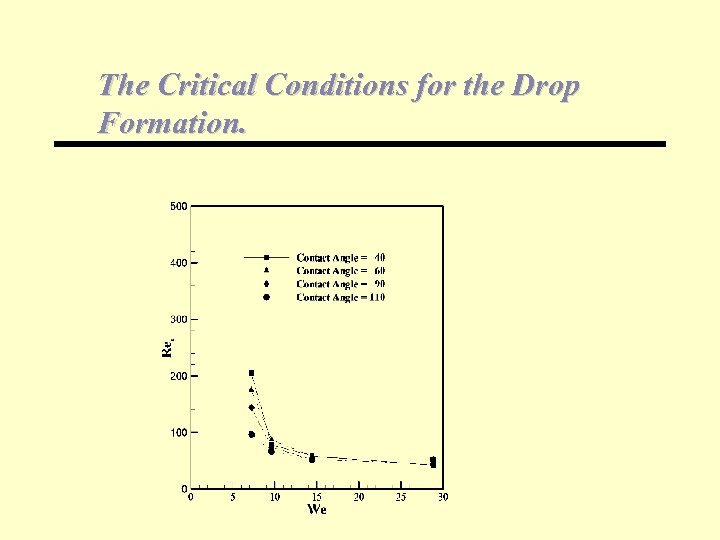The Critical Conditions for the Drop Formation.

The Critical Conditions for the Drop Formation.

Conclusion • Droplet-on-Orifice Impacting Droplet Generation • Mechanism: • Penetration of the portion of the liquid on top of the orifice; • Spreading of the mother drop on the solid surface; • Recoil of the mother drop; • Pull back of the penetrated liquid mass.

Conclusion • There is an optimum Di for smallest Df • There is an optimum Do for smallest Df • As Vi , Df ; • We , Ds ; • Re is not a proper scaling parameter (Re , V/Vi ); • Smallest drop size ratio of 1. 67 is achieved; • Drop velocity ratios of less than 0. 5 are achievable.