 Параллельный перенос Презентацию подготовила Перцева наталья
Параллельный перенос Презентацию подготовила Перцева наталья
 Пусть а – данный вектор. Построим равный ему вектор. Достроим до параллелограмма ММ 1 N 1 N. M 1 N 1 a M N
Пусть а – данный вектор. Построим равный ему вектор. Достроим до параллелограмма ММ 1 N 1 N. M 1 N 1 a M N
 Параллельный перенос Таким образом: Параллельным переносом на вектор а называется отображение плоскости на себя, при котором каждая точка М отображается в такую точку М 1, что вектор ММ 1 равен вектору а
Параллельный перенос Таким образом: Параллельным переносом на вектор а называется отображение плоскости на себя, при котором каждая точка М отображается в такую точку М 1, что вектор ММ 1 равен вектору а
 Параллельный перенос является движением, т. е. отображением плоскости на себя, сохраняющим расстояние M 1 a M N N 1 Доказательство: Пусть при параллельном переносе на вектор а точки M и N отображаются в точки M 1 и N 1. Так как все векторы равны. Следовательно: Векторы параллельны и равны, а значит четырехугольник ММ 1 N 1 N – параллелограмм.
Параллельный перенос является движением, т. е. отображением плоскости на себя, сохраняющим расстояние M 1 a M N N 1 Доказательство: Пусть при параллельном переносе на вектор а точки M и N отображаются в точки M 1 и N 1. Так как все векторы равны. Следовательно: Векторы параллельны и равны, а значит четырехугольник ММ 1 N 1 N – параллелограмм.
 Вывод: Значит, расстояние между векторами и точками равно. Таким образом, параллельный перенос сохраняет расстояние между точками и поэтому представляет собой движение.
Вывод: Значит, расстояние между векторами и точками равно. Таким образом, параллельный перенос сохраняет расстояние между точками и поэтому представляет собой движение.
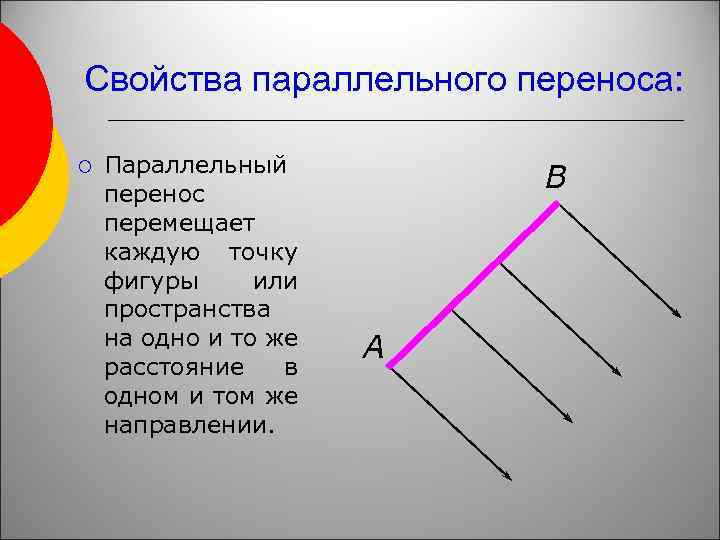 Свойства параллельного переноса: ¡ Параллельный перенос перемещает каждую точку фигуры или пространства на одно и то же расстояние в одном и том же направлении. В А
Свойства параллельного переноса: ¡ Параллельный перенос перемещает каждую точку фигуры или пространства на одно и то же расстояние в одном и том же направлении. В А
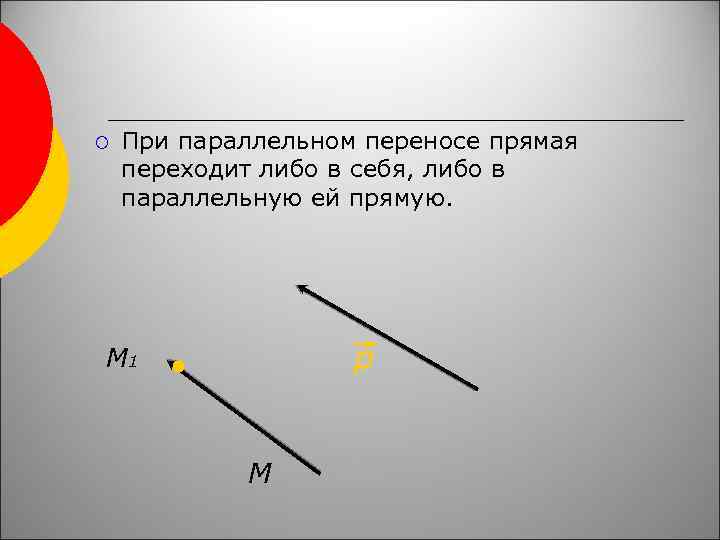 ¡ При параллельном переносе прямая переходит либо в себя, либо в параллельную ей прямую. p М 1 М
¡ При параллельном переносе прямая переходит либо в себя, либо в параллельную ей прямую. p М 1 М
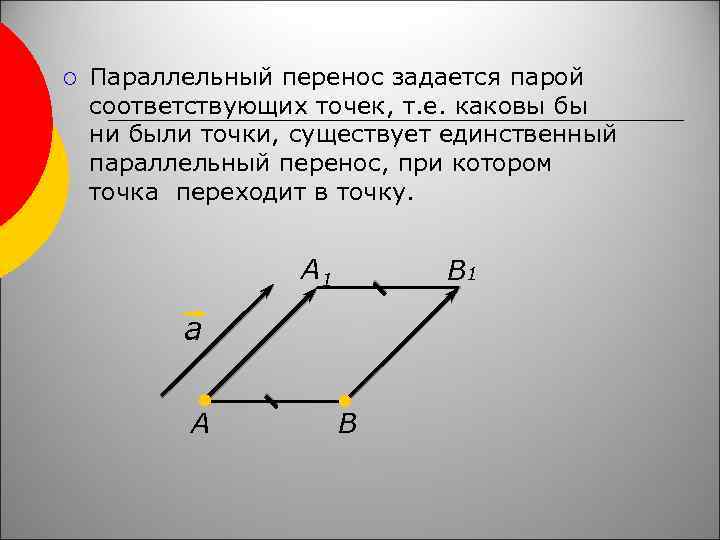 ¡ Параллельный перенос задается парой соответствующих точек, т. е. каковы бы ни были точки, существует единственный параллельный перенос, при котором точка переходит в точку. А 1 B 1 а А В
¡ Параллельный перенос задается парой соответствующих точек, т. е. каковы бы ни были точки, существует единственный параллельный перенос, при котором точка переходит в точку. А 1 B 1 а А В
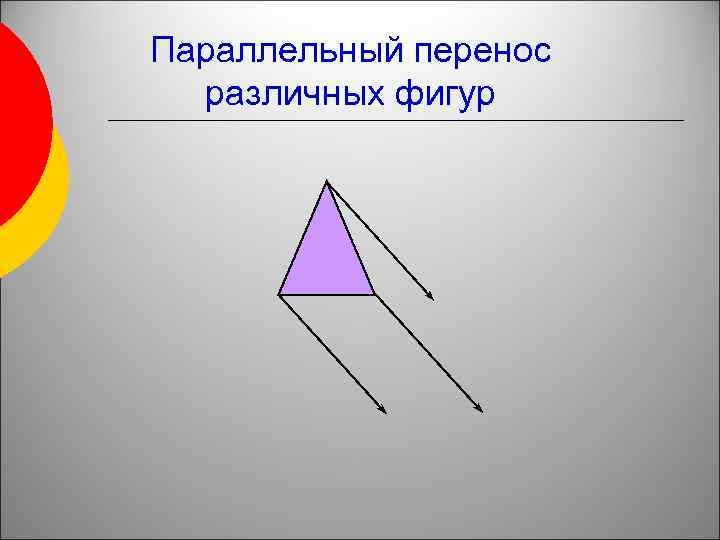 Параллельный перенос различных фигур
Параллельный перенос различных фигур
 Параллельный перенос в пространстве Параллельным переносом в пространстве называется такое преобразование, при котором произвольная точка (x; y; z) фигуры переходит в точку (x + a; y + b; z + c), где числа a, b, с одни и те же для всех точек (x; y; z).
Параллельный перенос в пространстве Параллельным переносом в пространстве называется такое преобразование, при котором произвольная точка (x; y; z) фигуры переходит в точку (x + a; y + b; z + c), где числа a, b, с одни и те же для всех точек (x; y; z).
 Параллельный перенос в пространстве обладает следующими свойствами: 1. Параллельный перенос есть движение. 2. При параллельном переносе точки смещаются по параллельным прямым на одно и то же расстояние. 3. При параллельном переносе каждая прямая переходит в параллельную ей прямую или в себя. 4. Каковы бы ни были точки A и A', существует единственный параллельный перенос, при котором точка A переходит в точку A'. 5. При параллельном переносе в пространстве каждая плоскость переходит либо в себя, либо в параллельную ей плоскость.
Параллельный перенос в пространстве обладает следующими свойствами: 1. Параллельный перенос есть движение. 2. При параллельном переносе точки смещаются по параллельным прямым на одно и то же расстояние. 3. При параллельном переносе каждая прямая переходит в параллельную ей прямую или в себя. 4. Каковы бы ни были точки A и A', существует единственный параллельный перенос, при котором точка A переходит в точку A'. 5. При параллельном переносе в пространстве каждая плоскость переходит либо в себя, либо в параллельную ей плоскость.
 Решим задачу C’ C D’ D A’ A B B’
Решим задачу C’ C D’ D A’ A B B’
 Спасибо за внимание
Спасибо за внимание