Параллельный перенос на плоскости Выполнил Красовский Дмитрий Студент

Параллельный перенос на плоскости Выполнил Красовский Дмитрий Студент группы М-2 ФМФИ

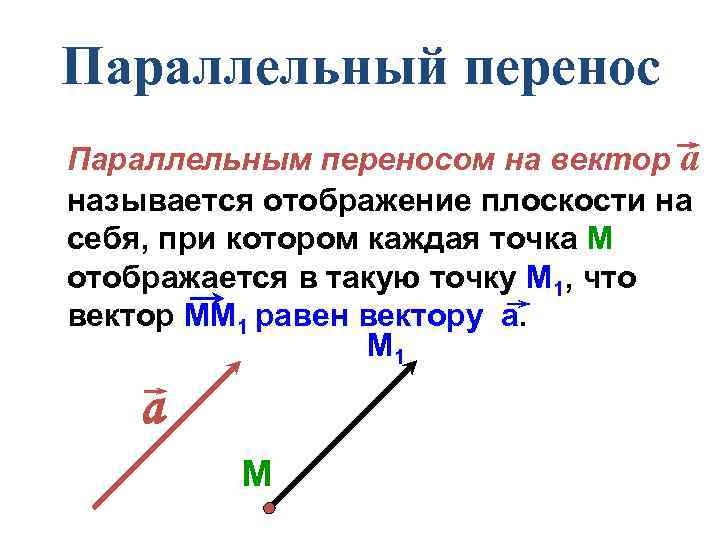Параллельный перенос Параллельным переносом на вектор а называется отображение плоскости на себя, при котором каждая точка М отображается в такую точку М 1, что вектор ММ 1 равен вектору а. М 1 а М

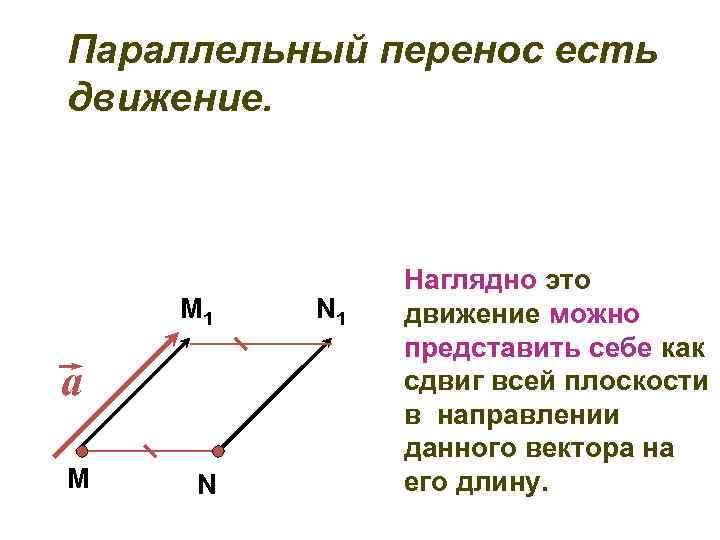Параллельный перенос есть движение. M 1 a М N N 1 Наглядно это движение можно представить себе как сдвиг всей плоскости в направлении данного вектора на его длину.

Наглядно параллельный перенос определяется как преобразование, при котором точки смещаются в одном и том же направлении на одно и то же расстояние (рис. 198). Такое определение не является математически строгим, потому что в нем употребляется выражение «в одном и том же направлении» , которое само нуждается в точном определении. В связи с этим параллельному переносу мы дадим другое, отвечающее тому же наглядному представлению, но уже строгое определение. Введем на плоскости декартовы координаты х, у. Преобразование фигуры F, при котором произвольная ее точка (х; у) переходит в точку (х + а; у + b), где а и b одни и те же для всех точек (х; у), называется параллельным переносом (рис. 199). Параллельный перенос задается формулами x' = x + а, у' = у + b.

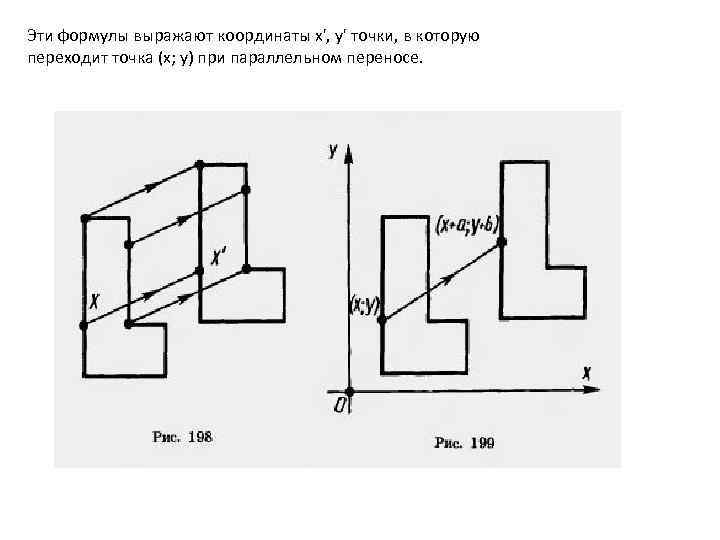Эти формулы выражают координаты х', у' точки, в которую переходит точка (х; у) при параллельном переносе.

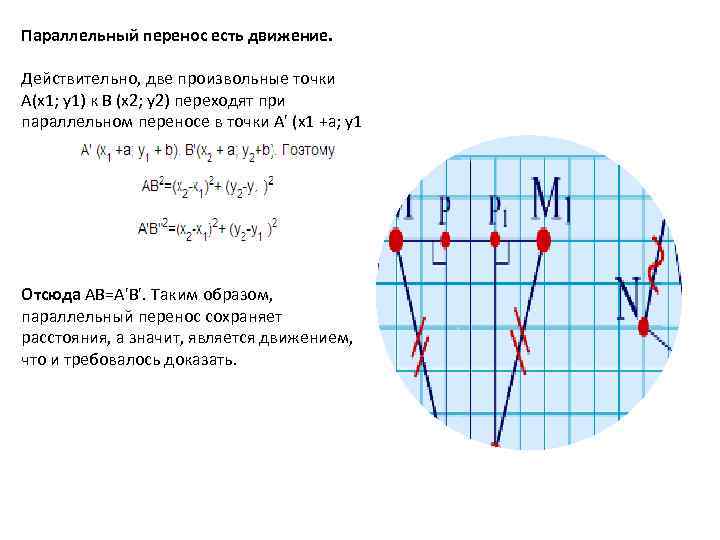Параллельный перенос есть движение. Действительно, две произвольные точки А(х1; у1) к В (х2; у2) переходят при параллельном переносе в точки А' (х1 +а; у1 + b), В'(х2 + а; y 2+b). Поэтому Отсюда АВ=А'В'. Таким образом, параллельный перенос сохраняет расстояния, а значит, является движением, что и требовалось доказать.

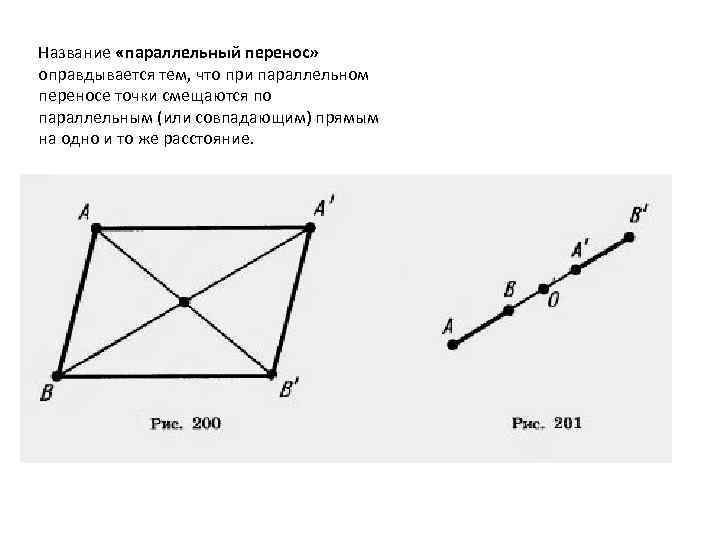Название «параллельный перенос» оправдывается тем, что при параллельном переносе точки смещаются по параллельным (или совпадающим) прямым на одно и то же расстояние.

Действительно, пусть точки A (x 1; y 1) и В (x 2; y 2) переходят в точки A'(x 1+а; y 1 + b) и В' (х2 + а; y 2 + b) (рис. 200). Середина отрезка АВ' имеет координаты. Те же координаты имеет и середина отрезка А'В. Отсюда следует, что диагонали четырехугольника АА'В'В пересекаются и точкой пересечения делятся пополам. Значит, этот четырехугольник — параллелограмм. А у параллелограмма противолежащие стороны А А' и ВВ' параллельны и равны. Заметим, что у параллелограмма АА'В'В параллельны и две другие противолежащие стороны — АВ и А 'В'. Отсюда следует, что при параллельном, переносе прямая переходит в параллельную прямую (или в себя).

Замечание. В предыдущем доказательстве предполагалось, что точка В не лежит на прямой АА'. В случае, когда точка В лежит на прямой АА', точка В' тоже лежит на этой прямой, так как середина отрезка АВ' совпадает с серединой отрезка ВА' (рис. 201). Значит, все точки А, В, А', В' лежат на одной прямой. Далее Таким образом, в этом случае точки А и В смещаются по прямой АВ на одно и то же расстояние а прямая АВ переходит в себя.

Параллельный перенос на плоскости в системе координат. Введем на плоскости систему координат O, X, Y. Преобразование фигуры F, при котором произвольная ее точка M (x; y) переходит в точку M' (x+a; y+b) , где a и b – одни и те же для всех точек (x; y), называется параллельным переносом.

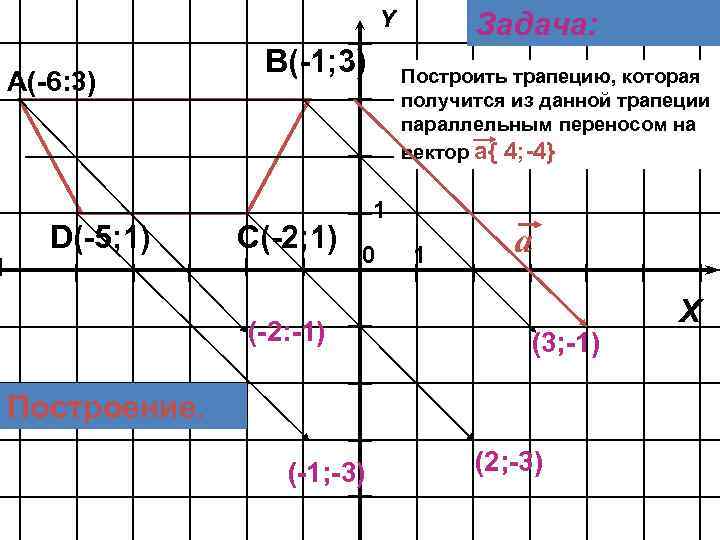Y А(-6: 3) D(-5; 1) В(-1; 3) С(-2; 1) Задача: Построить трапецию, которая получится из данной трапеции параллельным переносом на вектор а{ 4; -4} 1 0 (-2: -1) 1 а (3; -1) Построение. (-1; -3) (2; -3) X

Y В(-4; 3) А(-6; 1) С(-3; 3) D(-1; 1) 1 0 1 X Задача: Построить трапецию, которая получится из данной трапеции параллельным переносом на вектор АD (на вектор BC).

Y B 1(1; 3) C 1(2; 3) 1 A 1(-1; 1) 0 1 D 1(4; 1) X 1 вариант (ответ) 2 вариант

Y B 1 (-3; 3) C 1(-2; 3) A 1 (-5; 1) 1 D 1(0; 1) 0 1 X 2 вариант (ответ)