Параллельные вычисления. Анализ эффективности алгоритмов линейной алгебры Руководитель: Биллиг Владимир Арнольдович Автор: Старовойтов Игорь Викторович 1
Цель работы Оценка эффективности инструментариев параллельных вычислений -. Net TPL и Open MP. 2
Актуальность Роль параллельных вычислений возрастает; Существуют различные инструментарии, позволяющие организовать параллельные вычисления. 3
Предметная область В данной дипломной работе мы проводим разработку библиотеки параллельных алгоритмов для решения задач линейной алгебры. Главными объектами анализа являются последовательные и параллельные алгоритмы с применением соответствующих инструментов. 4
Задачи Основные операции над матрицами – основными объектами линейной алгебры: Умножение матриц; Вычисление определителя матрицы; Умножение n матриц (задача о порядке перемножения матриц); Решение систем линейных уравнений с n правыми частями; Возведение матрицы в степень; Обращение квадратных матриц. 5
TPL Основные преимущества Task Parallel Library: Минимум изменений при модификации кода; Parallel. For, Parallel. Foreach –распараллеливание циклов; Parallel. Invoke – распараллеливание задач. 6
Выбор программных средств разработки и проектирования Средства разработки: Платформа. Net Язык программирования: С# 7
Умножение матриц Результатом работы алгоритма является матрица C размерами m * n, где элементы матрицы вычисляются по формуле: где i = 1, 2, …m; j = 1, 2, …n. Модифицируем данный последовательный алгоритм. Всего мы имеем три цикла по m, n и q итераций соответственно. При этом итерации по m и n независимы. Итерации по q затрагивают общую переменную, поэтому не могут быть эффективно распараллелены. Возможны следующие варианты распределения итераций: Распределение задачи по m * n блоков; Распределение по m блоков. 8
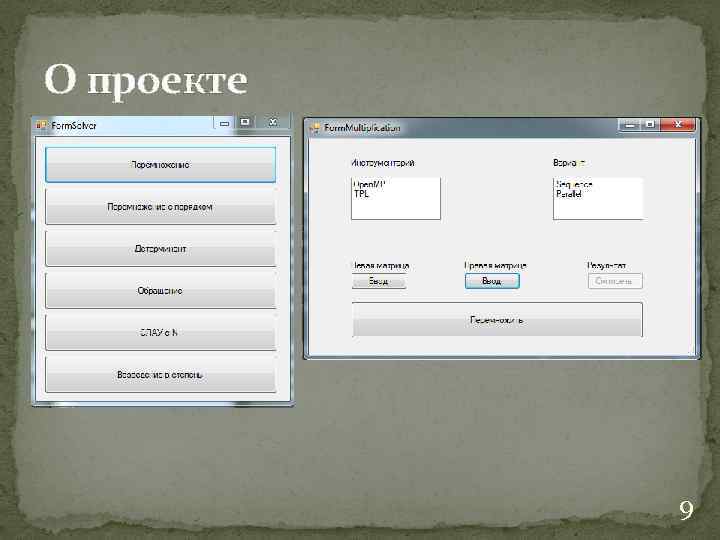
О проекте 9
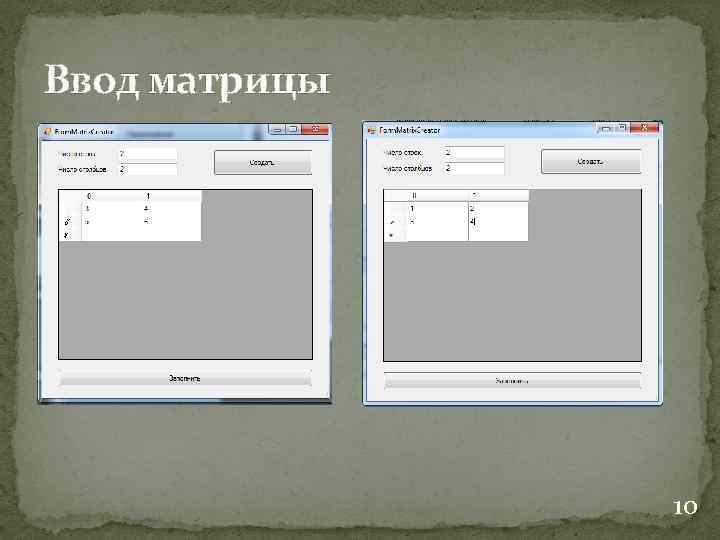
Ввод матрицы 10
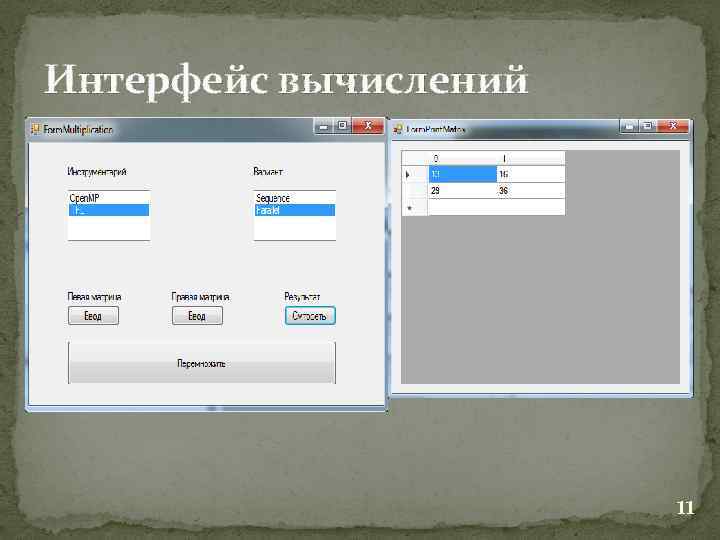
Интерфейс вычислений 11
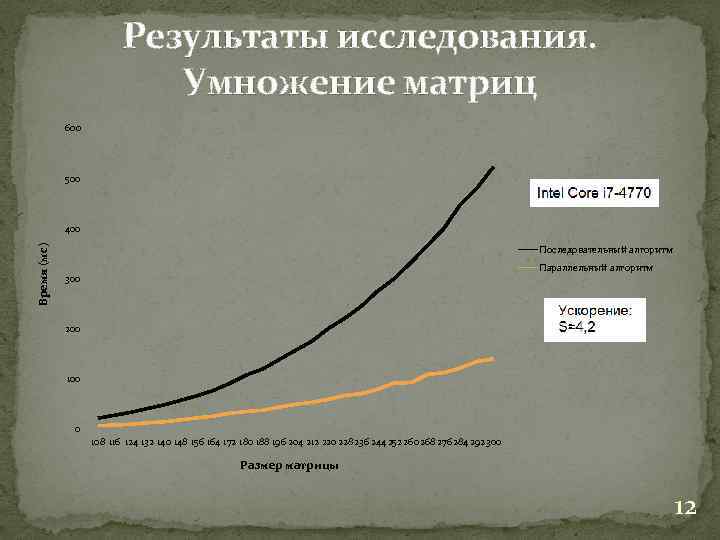
Результаты исследования. Умножение матриц 600 500 Время (мс) 400 Последовательный алгоритм Параллельный алгоритм 300 200 100 0 108 116 124 132 140 148 156 164 172 180 188 196 204 212 220 228 236 244 252 260268 276 284 292 300 Размер матрицы 12
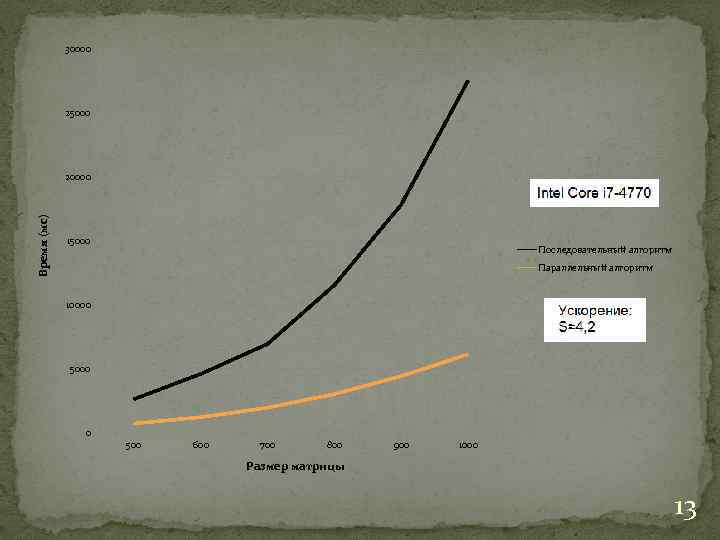
30000 25000 Время (мс) 20000 15000 Последовательный алгоритм Параллельный алгоритм 10000 5000 0 500 600 700 800 900 1000 Размер матрицы 13
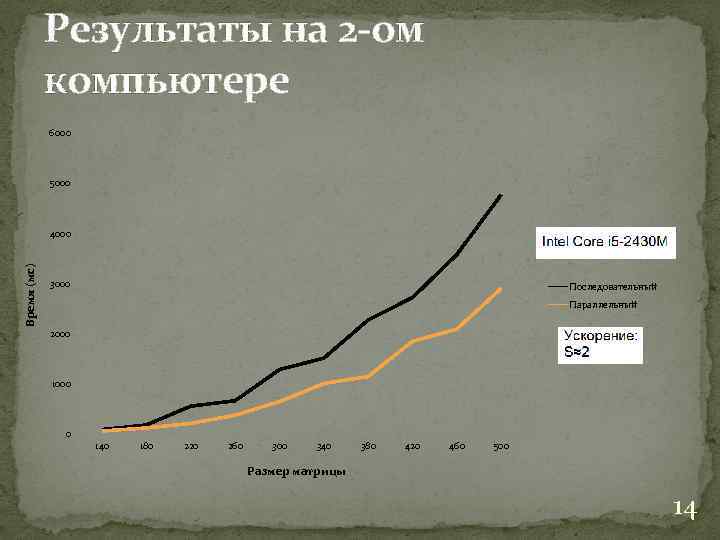
Результаты на 2 -ом компьютере 6000 5000 Время (мс) 4000 3000 Последовательный Параллельный 2000 1000 0 140 180 220 260 300 340 380 420 460 500 Размер матрицы 14
Как видно из результатов тестирования, последовательный алгоритм проигрывает параллельному алгоритму. На меньших размерах проигрыш идет незначительный, однако с увеличением размеров идет существенный отрыв. Результаты на разных компьютерах идентичны результатам полученным мною. Разница лишь в том, что время выполнения операций напрямую зависит от количество ядер компьютера. Чем больше ядер, тем больше и ускорение. Проведя сравнение результатов, стоит заметить ускорение примерно равно числу физических ядер процессора. 15
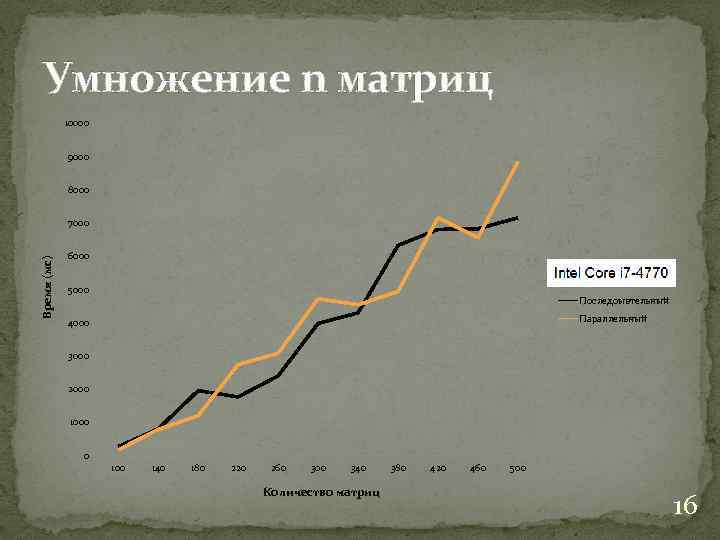
Умножение n матриц 10000 9000 8000 Время (мс) 7000 6000 5000 Последоывтельный Параллельный 4000 3000 2000 1000 0 100 140 180 220 260 300 340 Количество матриц 380 420 460 500 16
Итоги В данной работе мы затронули широкий спектр задач. Как видно из результатов исследования параллельный алгоритм не всегда эффективный по сравнению с последовательным. Эффективность зависит от количество распараллеленных частей в алгоритмах задач. Например «Умножение матриц» распараллелилась хорошо, а вот «Умножение n матриц» имеет минимум параллельного кода, поэтому параллелизм дал минимум ускорения. 17
Спасибо за внимание! 18
Скачать презентацию Параллельные вычисления Анализ эффективности алгоритмов линейной алгебры Руководитель
Старовойтов.pptx