Параллельность прямых и плоскостей в пространстве Каракулова М

Параллельность прямых и плоскостей в пространстве. Каракулова М. С. 2 о 2

Содержание 1. Аксиомы группы С 2. Следствие из аксиом 3. Доказательство 4. Взаимное расположение прямых в пространстве 5. Теорема о параллельных прямых 6. Следствие из теоремы 7. Признак параллельности прямой и плоскости 8. Признак параллельности прямых 9. Признак параллельности 2 -х плоскостей 10. Теорема 11. Свойство параллельных плоскостей 12. Задача

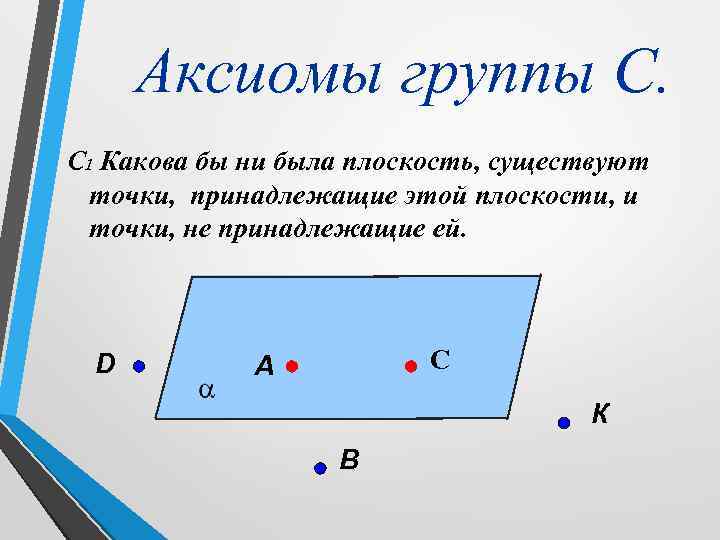Аксиомы группы С. С 1 Какова бы ни была плоскость, существуют точки, принадлежащие этой плоскости, и точки, не принадлежащие ей. D А С К B

Аксиомы группы С. С 2 Если две различные плоскости имеют общую точку, то они пересекаются по прямой, проходящей через эту точку. С а

Аксиомы группы С. С 3 Если две различные прямые имеют общую точку, то через них можно провести плоскость, и притом только одну. С a b

Следствия из аксиом m М α Т Через любую прямую и не принадлежащую ей точку можно провести плоскость, и притом только одну.

Следствия из аксиом В m А α Т Если две точки прямой принадлежат плоскости, то вся прямая принадлежит плоскости

Следствия из аксиом В М А α Т Через 3 точки, не лежащие на одной прямой, можно провести плоскость, и притом только одну.

Доказательство Проведем АВ прямые АВ и АМ. Они различны (т. к. А, В, М не лежат на одной прямой), но имеют общую точку А. Тогда по аксиоме С 3 через них можно просвети плоскость и притом только одну.

Взаимное расположение прямых в пространстве.

Пересекающиеся прямые - это прямые, лежащие в одной плоскости и имеющие одну общую точку, которую называют точкой пересечения. а∩b=O b O а β

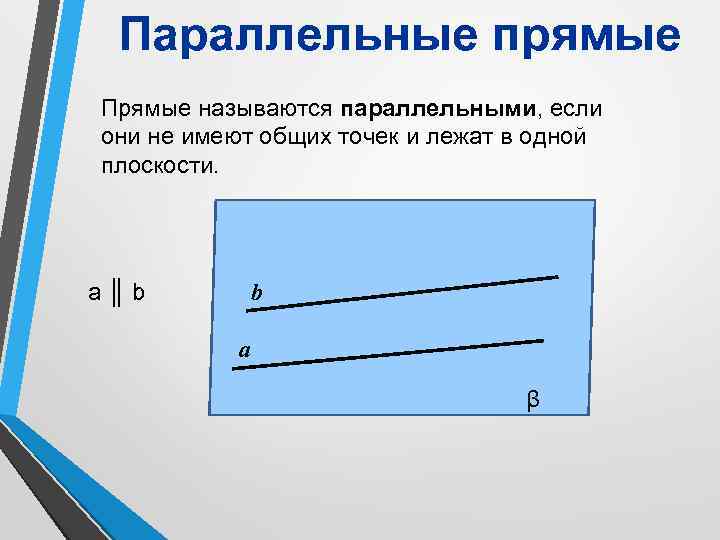Параллельные прямые Прямые называются параллельными, если они не имеют общих точек и лежат в одной плоскости. a ║ b b а β

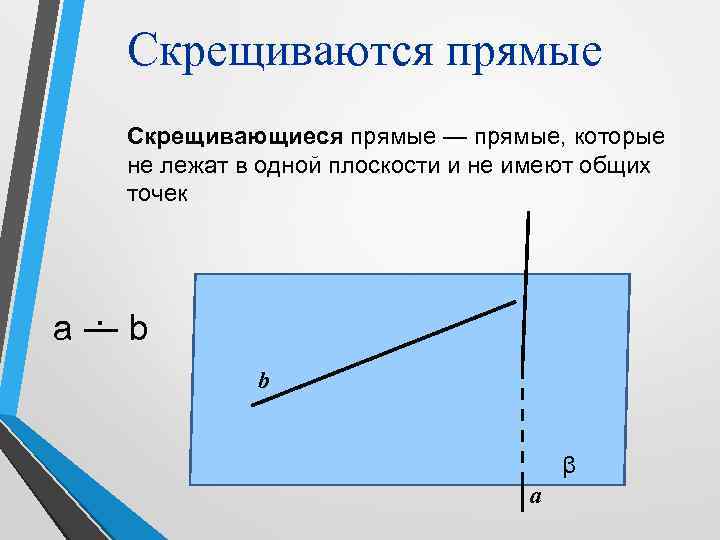Скрещиваются прямые Скрещивающиеся прямые — прямые, которые не лежат в одной плоскости и не имеют общих точек . a ― b b β а

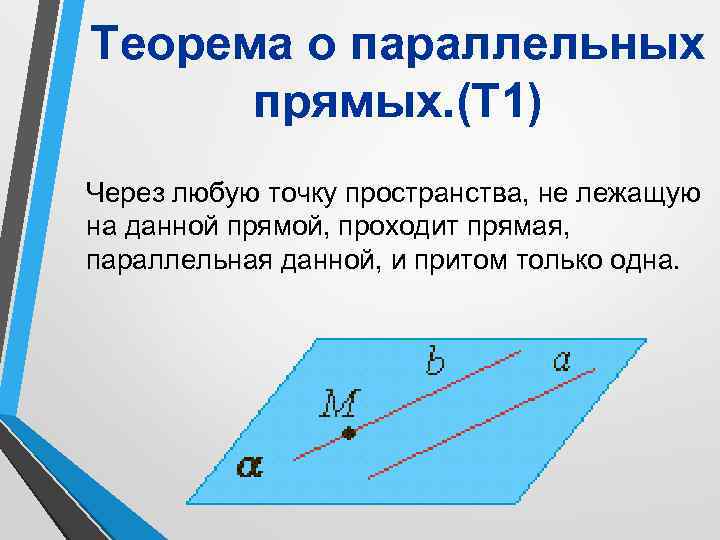Теорема о параллельных прямых. (Т 1) Через любую точку пространства, не лежащую на данной прямой, проходит прямая, параллельная данной, и притом только одна.

Признак параллельности прямых Две прямые, параллельные третьей прямой, параллельны другу. Если: a ║ c и b ║ c, то а ║ b С

Признак параллельности прямой и плоскости Если прямая, не лежащая в данной плоскости, параллельна какой-нибудь прямой, лежащей в этой плоскости, то она параллельна и самой плоскости.

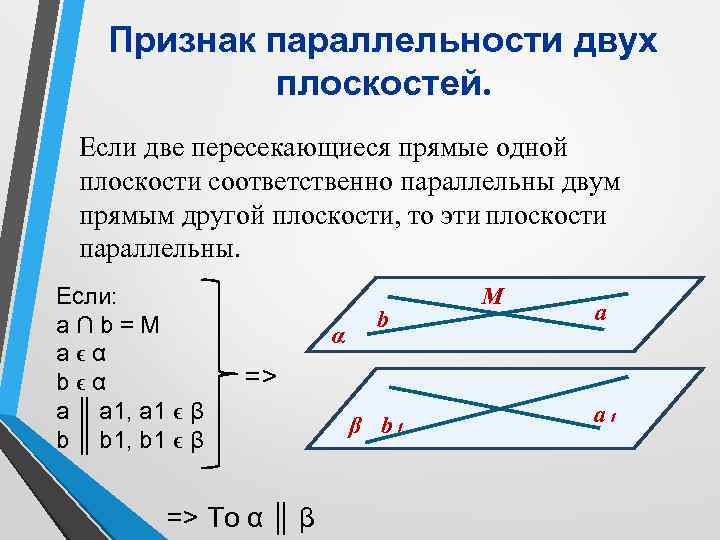Признак параллельности двух плоскостей. Если две пересекающиеся прямые одной плоскости соответственно параллельны двум прямым другой плоскости, то эти плоскости параллельны. Если: a ∩ b = M a ϵ α b ϵ α a ║ a 1, a 1 ϵ β b ║ b 1, b 1 ϵ β α b M а => => То α ║ β β b₁ а₁

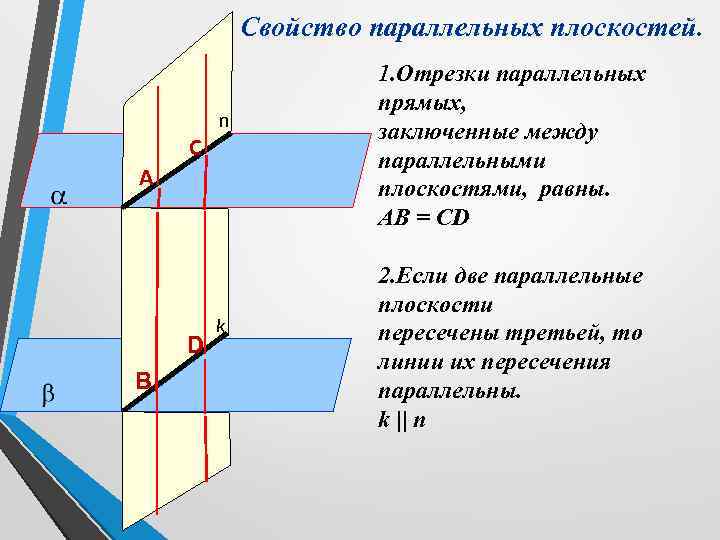Свойство параллельных плоскостей. С 1. Отрезки параллельных прямых, заключенные между параллельными плоскостями, равны. AB = CD D 2. Если две параллельные плоскости пересечены третьей, то линии их пересечения параллельны. k || n n А В k

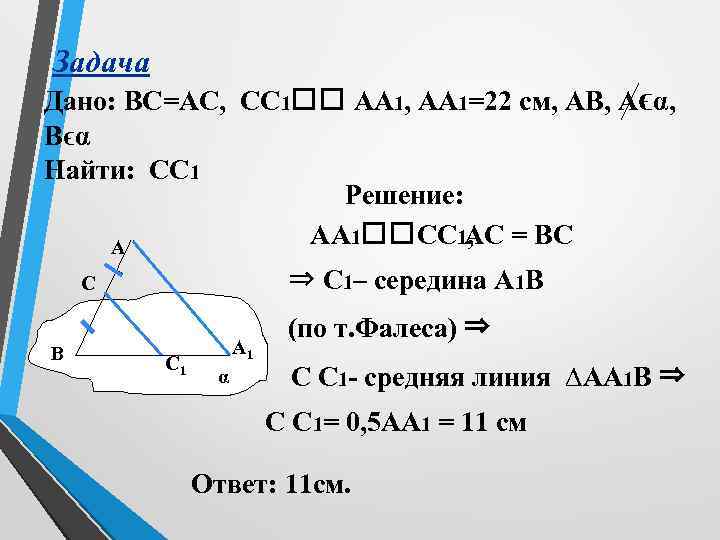Задача Дано: ВС=АС, СС 1 АА 1, АА 1=22 см, АВ, Аϵα, Вϵα Найти: СС 1 Решение: АА 1 СС 1 АС = ВС , А ⇒ С 1– середина А 1 В С 1 А 1 α (по т. Фалеса) ⇒ С С 1 - средняя линия ∆АА 1 В ⇒ С С 1= 0, 5 АА 1 = 11 см Ответ: 11 см.