Parallelizing the Data Cube Ph D Oral Defence

Parallelizing the Data Cube Ph. D Oral Defence Todd Eavis July 23, 2003

Overview ● Motivation for Parallel, Relational OLAP ● Core Algorithms and Methods ● Primary Systems Contributions ● Experimental Evaluation and Results ● Conclusions and Future Work

– Motivation for Parallel, Relational OLAP – Core Algorithms and Methods – Primary Systems Contributions – Experimental Evaluation and Results – Conclusions and Future Work

Why study OLAP and the Data Cube? ● On-line Analytical Processing: the foundation for a range of essential business applications – ● ● ● sales and marketing analysis, planning and budgeting 4 billion dollar industry by 2005 Data Cube: a core OLAP construct, first proposed in 1996 by Gray et al [GBLP], that supports sophisticated multi-dimensional data analysis Relevance to the Research Community? Results of Citeseer queries: – – ● OLAP: 797 papers Data Cube: 362 papers Our interest: Data Cube Generation and Querying

Scale of OLAP Data Warehouses ● ● ● Average size of production data warehouses currently 700 GB [survey. com/Olap Report] Expected to reach 4 TB by 2004 1/3 currently <= 50 GB. In two years, this number will drop to just 6% Biggest data warehouses growing by a factor of 20 [Winter Report] Biggest expected to exceed 100 TB within 2 years Our Interest: Exploiting Parallel Algorithms

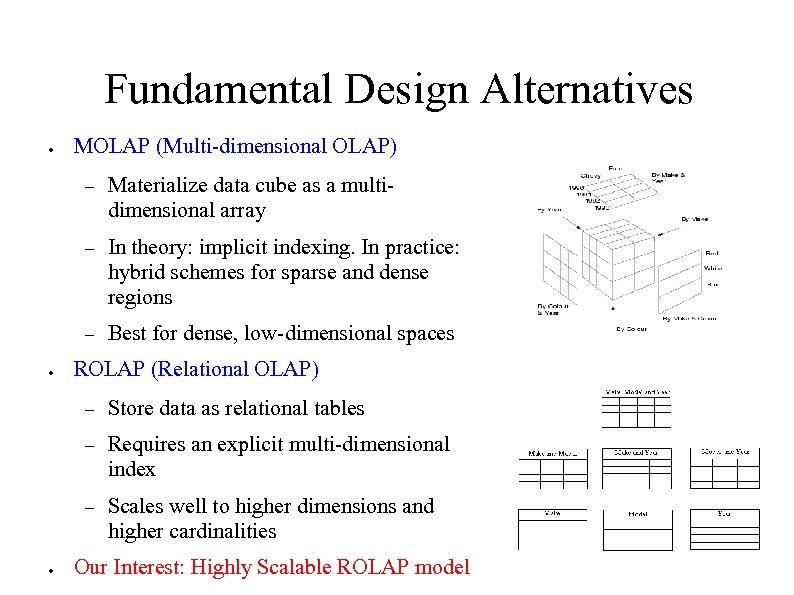
Fundamental Design Alternatives ● MOLAP (Multi-dimensional OLAP) – – In theory: implicit indexing. In practice: hybrid schemes for sparse and dense regions – ● Materialize data cube as a multidimensional array Best for dense, low-dimensional spaces ROLAP (Relational OLAP) – – Requires an explicit multi-dimensional index – ● Store data as relational tables Scales well to higher dimensions and higher cardinalities Our Interest: Highly Scalable ROLAP model

– Motivation for Parallel, Relational OLAP – Core Algorithms and Methods – Primary Systems Contributions – Experimental Evaluation and Results – Conclusions and Future Work

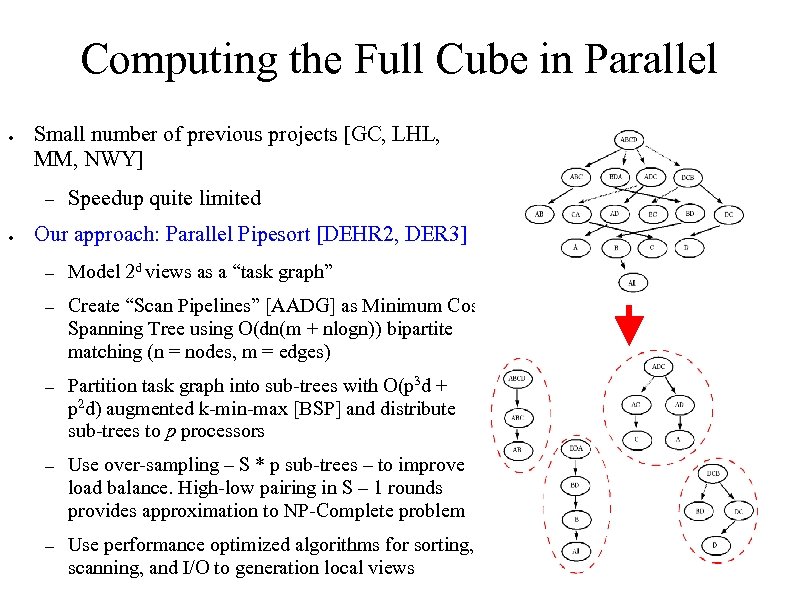
Computing the Full Cube in Parallel ● Small number of previous projects [GC, LHL, MM, NWY] – ● Speedup quite limited Our approach: Parallel Pipesort [DEHR 2, DER 3] – Model 2 d views as a “task graph” – Create “Scan Pipelines” [AADG] as Minimum Cost Spanning Tree using O(dn(m + nlogn)) bipartite matching (n = nodes, m = edges) – Partition task graph into sub-trees with O(p 3 d + p 2 d) augmented k-min-max [BSP] and distribute sub-trees to p processors – Use over-sampling – S * p sub-trees – to improve load balance. High-low pairing in S – 1 rounds provides approximation to NP-Complete problem – Use performance optimized algorithms for sorting, scanning, and I/O to generation local views

Computing Partial Cubes in Parallel ● ● ● Important in practice for environments with higher dimensions and/or specific visualization needs Little previous work, only partial solutions [BR, GC, SAG] Our approach: Greedy algorithms for “Schedule Tree” construction [DER 2, DER 5] – Solution consists of algorithms for generating efficieint “Essential Trees” (red) and algorithms for adding beneficial non-selected nodes (blue) – Greedy method: record “ state” information in Plan Objects. Incrementally add nodes with maximum benefit – Pre-sorting “candidate” views by estimated size can reduce run-time from O(n 3) to O(n 2) – O(d*n) heuristic extensions for higher dimensional space. A “confidence factor” β limits risk

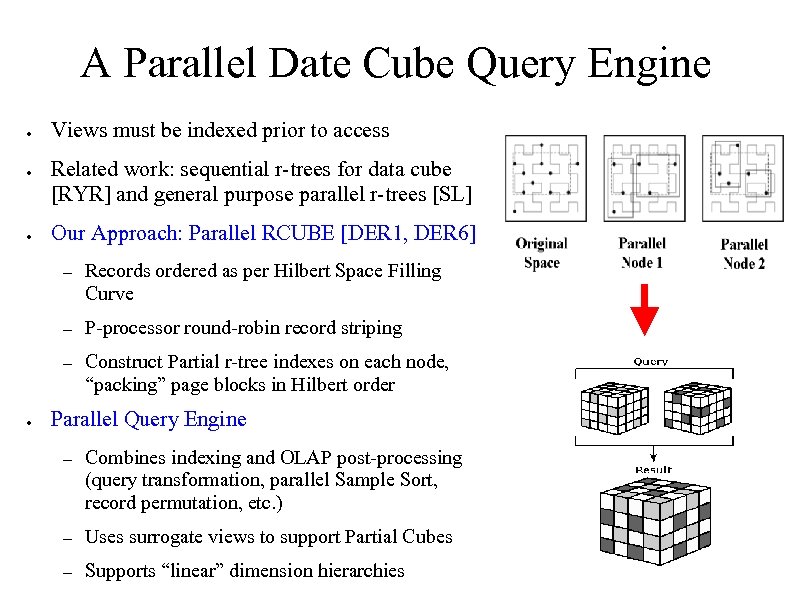
A Parallel Date Cube Query Engine ● ● ● Views must be indexed prior to access Related work: sequential r-trees for data cube [RYR] and general purpose parallel r-trees [SL] Our Approach: Parallel RCUBE [DER 1, DER 6] – – P-processor round-robin record striping – ● Records ordered as per Hilbert Space Filling Curve Construct Partial r-tree indexes on each node, “packing” page blocks in Hilbert order Parallel Query Engine – Combines indexing and OLAP post-processing (query transformation, parallel Sample Sort, record permutation, etc. ) – Uses surrogate views to support Partial Cubes – Supports “linear” dimension hierarchies

The Virtual Data Cube ● ● Motivation: Hide the complexity of Data Cube algorithms and implementation Requires no knowledge of: – Format or extent of indexing – Degree of materialization (full or partial) – Representation of hierarchies – Physical order of view attributes – Degree of parallelism

– Motivation for Parallel, Relational OLAP – Core Algorithms and Methods – Primary Systems Contributions – Experimental Evaluation and Results – Conclusions and Future Work

Systems Overview ● Full, robust Data Cube “prototype” [DER 4] ● Approximately 20, 000 lines of code – ● ● C/C++, LEDA, MPI, STL Template-based graph algorithms Designed for, and evaluated on, contemporary parallel machines: – – ● “Shared nothing” Linux cluster (Dalhousie) “Shared disk” Sun. Fire multi-processor (HPCVL) Supporting systems include: – Flex/Bison based data generator – Batch query generator

Key Performance Issues ● Dynamic selection of “best” sorting algorithm – ● Minimization of data movement – ● Use of horizontal and vertical indirection New pipeline aggregation algorithm – ● Radix sort versus quicksort “Lazy” aggregation Streamlined I/O – I/O manager – Independent I/O and computation threads

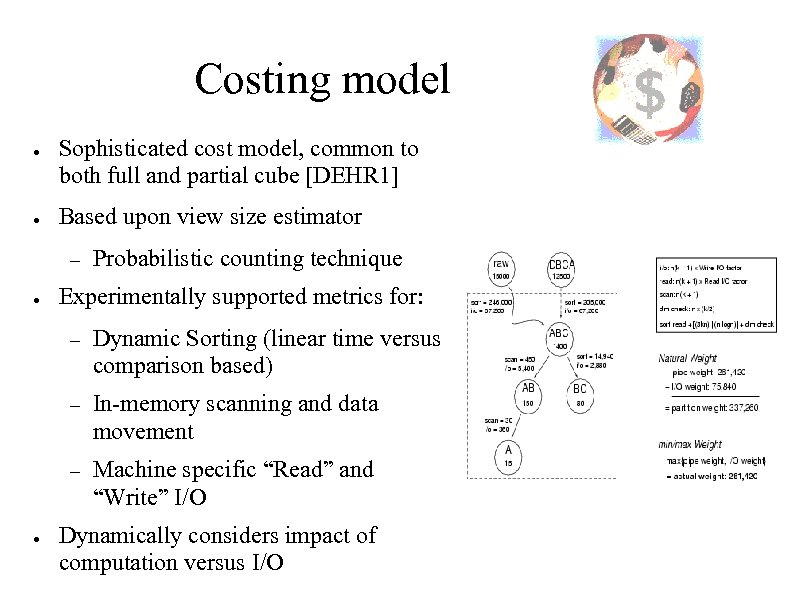
Costing model ● ● Sophisticated cost model, common to both full and partial cube [DEHR 1] Based upon view size estimator – ● Probabilistic counting technique Experimentally supported metrics for: – – In-memory scanning and data movement – ● Dynamic Sorting (linear time versus comparison based) Machine specific “Read” and “Write” I/O Dynamically considers impact of computation versus I/O

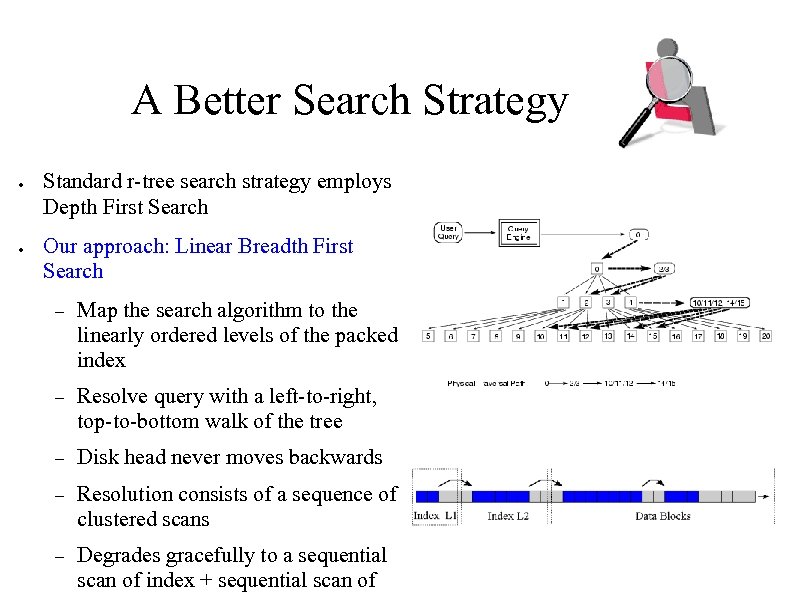
A Better Search Strategy ● ● Standard r-tree search strategy employs Depth First Search Our approach: Linear Breadth First Search – Map the search algorithm to the linearly ordered levels of the packed index – Resolve query with a left-to-right, top-to-bottom walk of the tree – Disk head never moves backwards – Resolution consists of a sequence of clustered scans – Degrades gracefully to a sequential scan of index + sequential scan of

– Motivation for Parallel, Relational OLAP – Core Algorithms and Methods – Primary Systems Contributions – Experimental Evaluation and Results – Conclusions and Future Work

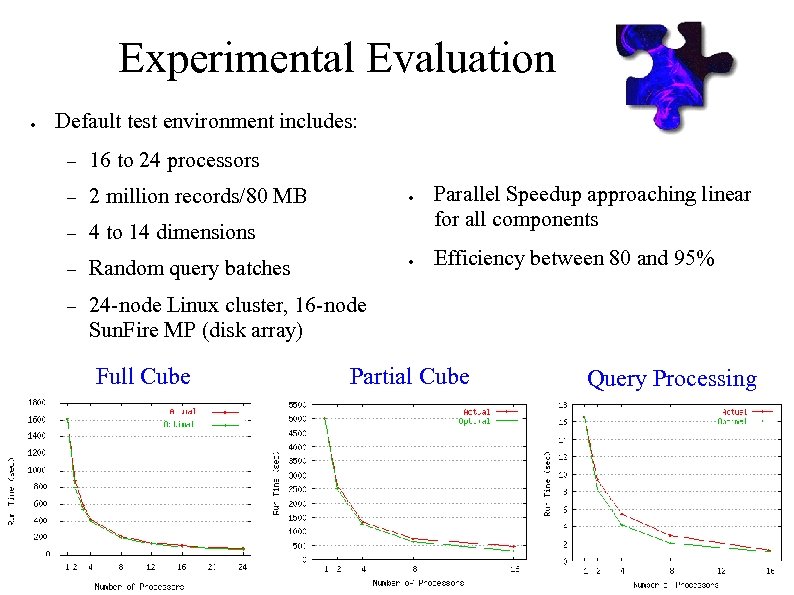
Experimental Evaluation ● Default test environment includes: – 16 to 24 processors – 2 million records/80 MB – 4 to 14 dimensions – Random query batches – 24 -node Linux cluster, 16 -node Sun. Fire MP (disk array) Full Cube ● ● Parallel Speedup approaching linear for all components Efficiency between 80 and 95% Partial Cube Query Processing

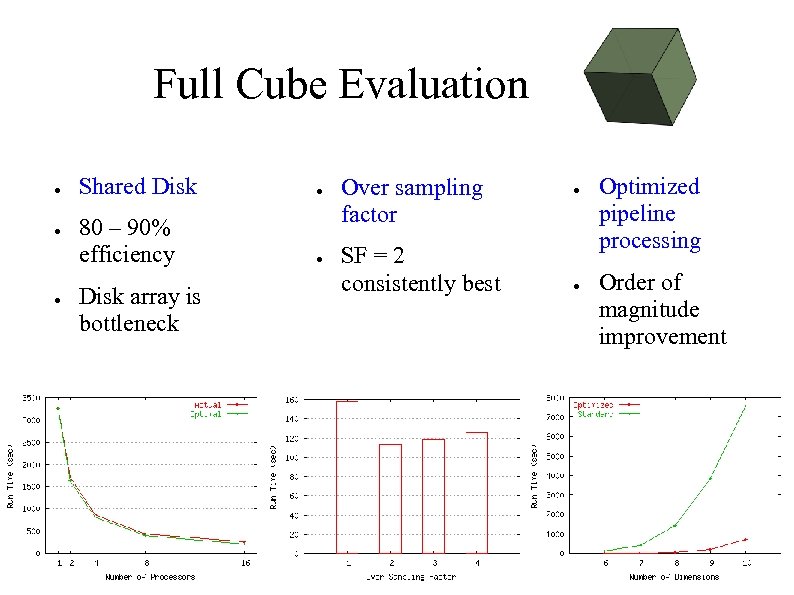
Full Cube Evaluation ● ● ● Shared Disk ● 80 – 90% efficiency ● Disk array is bottleneck Over sampling factor SF = 2 consistently best ● ● Optimized pipeline processing Order of magnitude improvement

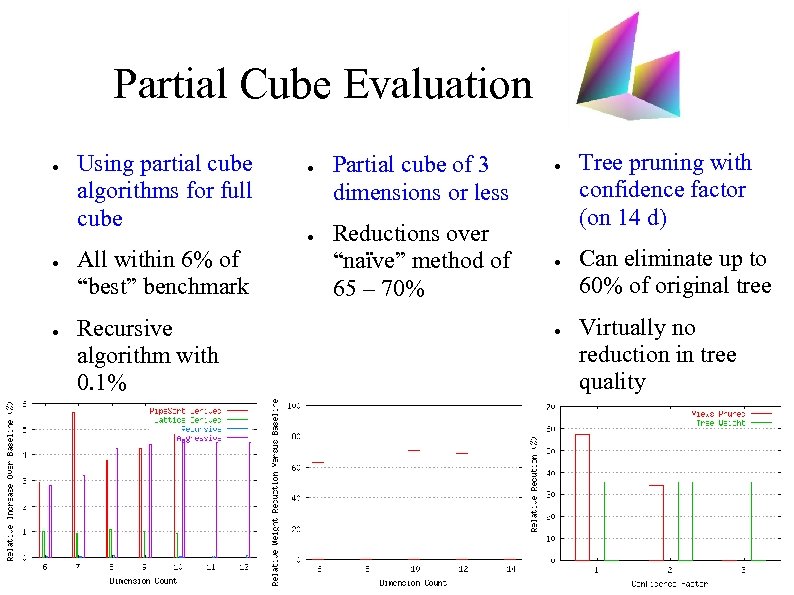
Partial Cube Evaluation ● ● ● Using partial cube algorithms for full cube All within 6% of “best” benchmark Recursive algorithm with 0. 1% ● ● Partial cube of 3 dimensions or less Reductions over “naïve” method of 65 – 70% ● ● ● Tree pruning with confidence factor (on 14 d) Can eliminate up to 60% of original tree Virtually no reduction in tree quality

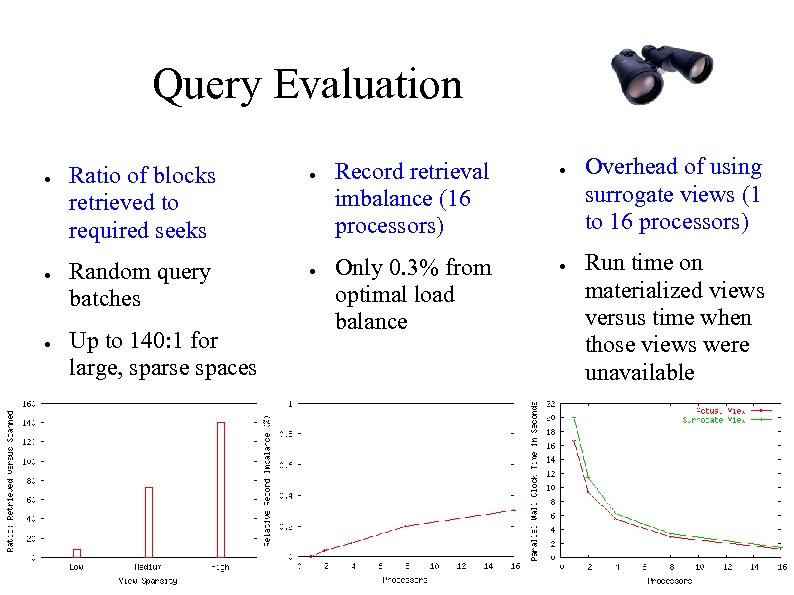
Query Evaluation ● ● ● Ratio of blocks retrieved to required seeks Random query batches Up to 140: 1 for large, sparse spaces ● ● Record retrieval imbalance (16 processors) Only 0. 3% from optimal load balance ● ● Overhead of using surrogate views (1 to 16 processors) Run time on materialized views versus time when those views were unavailable

– Motivation for Parallel, Relational OLAP – Core Algorithms and Methods – Primary Systems Contributions – Experimental Evaluation and Results – Conclusions and Future Work

Thesis Conclusions ● ● ROLAP a viable alternative to MOLAP in parallel setting Partial cubes can be efficiently generated ROLAP cubes can be efficiently indexed Virtual cube abstraction can be efficiently supported

Research Highlights ● First parallel ROLAP system in the Data Cube literature ● A balanced approach to data cube research – – Systems engineering – ● Algorithm design Extensive performance analysis Evaluated on contemporary parallel machines – – ● Commodity-style shared nothing cluster Shared disk architectures Integration of three “independent” data cube research projects into a single cohesive OLAP framework – the Virtual Cube

Future Work ● Automated partial cube specification – ● Extension of “virtual cube” Parallel Query optimization – In addition to range queries or linear hierarchies – High volume query environments ● OLAP visualization ● New projects are building on the current base – Generation of Iceberg Cubes – Mining of association rules

Thank You! References: Our own Virtual Data Cube Research References: The Data Cube Literature DEHR 1 F. Dehne, T. Eavis, S. Hambrusch and A. Rau-Chaplin, Parallelizing The Data Cube, Parallel and Distributed Databases: An International Journal, 2001 GBLP J. Gray and A. Bosworth and A. Layman and H. Pirahesh", Data Cube: A Relational Aggregation Operator Generalizing Group-By, Cross-Tab, and Sub. Totals", ICDE, 1996 DER 1 F. Dehne, Todd Eavis, A. Rau-Chaplin, Distributed Multidimensional ROLAP Indexing for the Data Cube, CCGrid, 2003. GC S. Goil and A. Choudhary, A Parallel Scalable Infrastructure for OLAP and Data Mining, IDEAS, 1999 LHL H. Lu, X. Huang and Z. Li, , Computing Data Cubes Using Massively DER 2 F. Dehne, T. Eavis and A. Rau-Chaplin, Computing Partial Data Cubes for Parallel Data Warehousing Applications, Euro PVM-MPI, 2001. Parallel Processors, PCW '97, 1997 DER 3 F. Dehne, T. Eavis, and A. Rau-Chaplin, Coarse Grained Parallel On- MM S. Muto and M. Kitsuregawa, A dynamic Load Balancing Strategy for Parallel Datacube Computation, WDW O, 1999 Line Analytical Processing (OLAP) For Data Mining, ICCS, 2001. DER 4 F. Dehne, T. Eavis, and A. Rau-Chaplin, A Cluster Architecture for NWY R. Ng, A. Wagner and Y. Yin, Iceberg-cube Computation with PC Clusters, SIGMOD, 2001 Parallel Data Warehousing, CCGrid, 2001. DEHR 2 F. Dehne, S. Hambrusch, T. Eavis, and A. Rau-Chaplin, Parallelizing The Data Cube, ICDT, 2001. AADG S. Agarwal and R. Agrawal and P. Deshpande and A. Gupta and J. Naughton and R. Ramakrishnan and S. Sarawagi, On the Computation of Multidimensional aggregates, VLDB, 1996 CHER Y. Chen, F. Dehne, Todd Eavis, A. Rau-Chaplin, Parallel ROLAP BSP R. Becker and S. Schach and Y. Perl, A shifting algorithm for min-max tree Data Cube Construction on Shared Nothing Multi-Processors, IPDPS, 2003. partitioning, Journal of the ACM, 1982 BR K. Beyer and R. Ramakrishnan, Bottom-up computation of sparse and Iceberg DER 5 F Dehne, T. Eavis, and A. Rau-Chaplin, Computing Partial Data CUBEs, SIGMOD, 1999 Cubes, Submitted to HICCS, 2003. RYR N. Roussopoulos and Y. Kotidis and M. Roussopolis, Cubetree: Organization of the bulk incremental updates on the data cube , SIGMOD, 1997 DER 6 F Dehne, T. Eavis, and A. Rau-Chaplin, RCUBE: Parallel Multi. Dimensional ROLAP Indexing, Submitted to Journal of to Data Mining and SL B. Schnitzer and S. Leutenegger, Master-client r-trees: a new parallel Knowledge Discovery. , 2003 architecture, SSDM, 1999