Параллелепипед. Тетраэдр. КОНУС Понятие многогранника Поверхность,






















parallelepiped._tetraedr._secheniya.ppt
- Размер: 4.2 Мб
- Автор:
- Количество слайдов: 94
Описание презентации Параллелепипед. Тетраэдр. КОНУС Понятие многогранника Поверхность, по слайдам
 Параллелепипед. Тетраэдр.
Параллелепипед. Тетраэдр.
 КОНУС
КОНУС
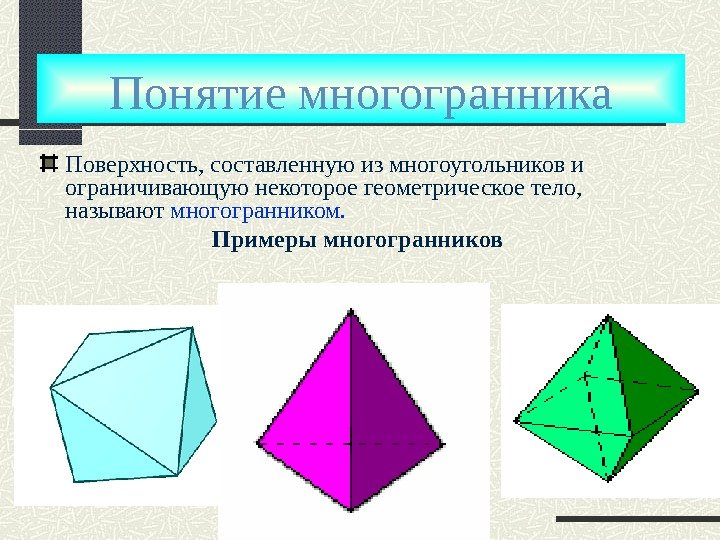
 Понятие многогранника Поверхность, составленную из многоугольников и ограничивающую некоторое геометрическое тело, называют многогранником. Примеры многогранников
Понятие многогранника Поверхность, составленную из многоугольников и ограничивающую некоторое геометрическое тело, называют многогранником. Примеры многогранников
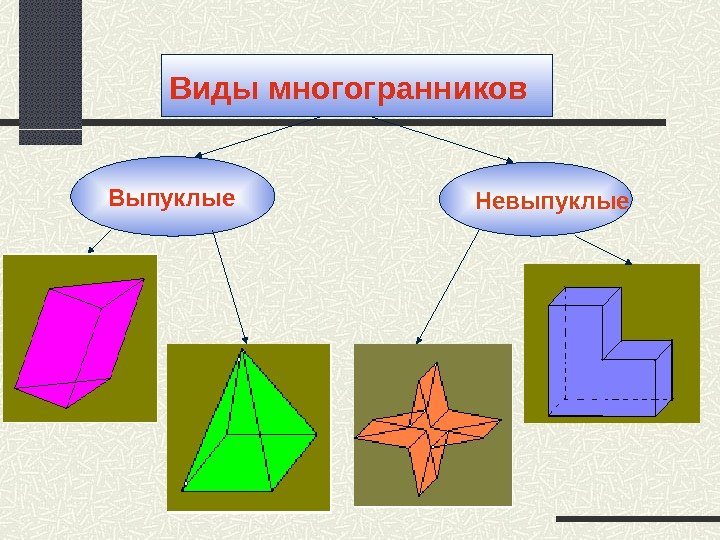
 Виды многогранников Выпуклые Невыпуклые
Виды многогранников Выпуклые Невыпуклые
 Примеры многогранников Большой курносый икосододекаэдр
Примеры многогранников Большой курносый икосододекаэдр
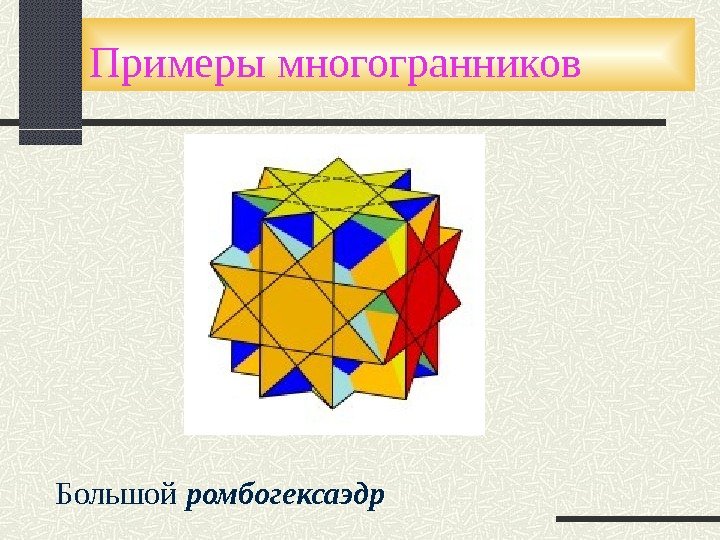
 Примеры многогранников Большой ромбогексаэдр
Примеры многогранников Большой ромбогексаэдр
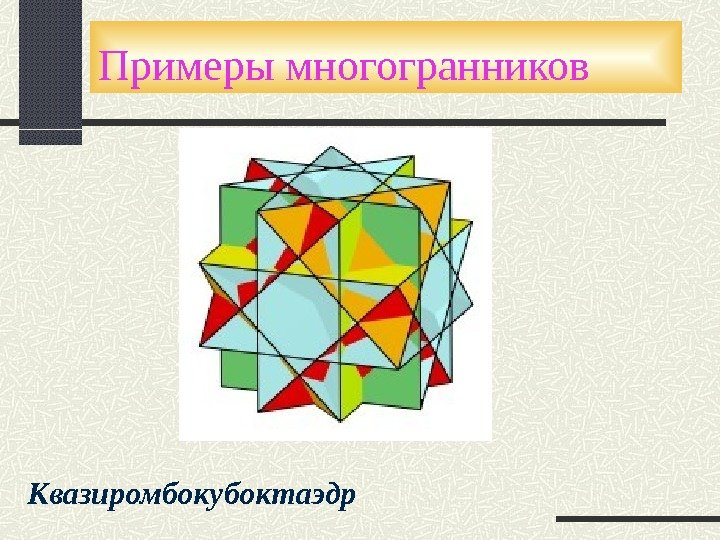
 Примеры многогранников Квазиромбокубоктаэдр
Примеры многогранников Квазиромбокубоктаэдр
 Выпуклый многогранник Многогранник называется выпуклым , если он расположен по одну сторону от плоскости каждой его грани. Все грани выпуклого многогранника являются выпуклыми многоугольниками. В выпуклом многограннике сумма всех плоских углов при каждой его вершине меньше 360 градусов.
Выпуклый многогранник Многогранник называется выпуклым , если он расположен по одну сторону от плоскости каждой его грани. Все грани выпуклого многогранника являются выпуклыми многоугольниками. В выпуклом многограннике сумма всех плоских углов при каждой его вершине меньше 360 градусов.
 Призма Призмой называется многогранник , который состоит из двух плоских многоугольников, лежащих в разных плоскостях и совмещаемых параллельным переносом, и всех отрезков, соединяющих соответствующие точки этих многоугольников.
Призма Призмой называется многогранник , который состоит из двух плоских многоугольников, лежащих в разных плоскостях и совмещаемых параллельным переносом, и всех отрезков, соединяющих соответствующие точки этих многоугольников.
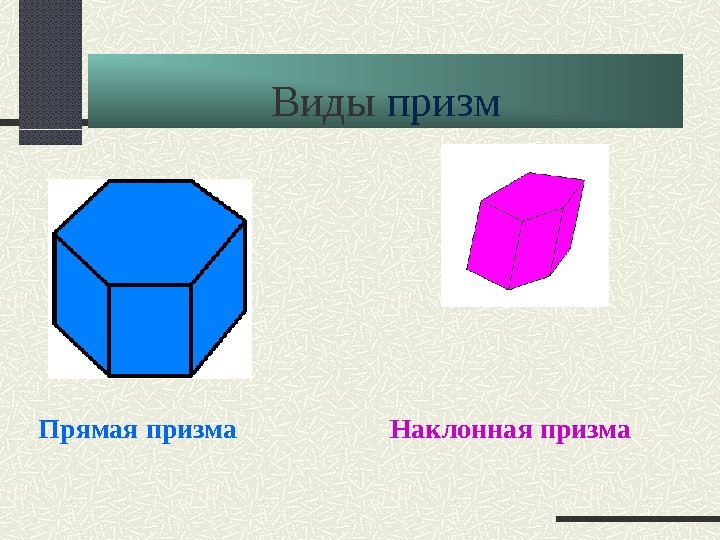
 Виды призм Прямая призма Наклонная призма
Виды призм Прямая призма Наклонная призма
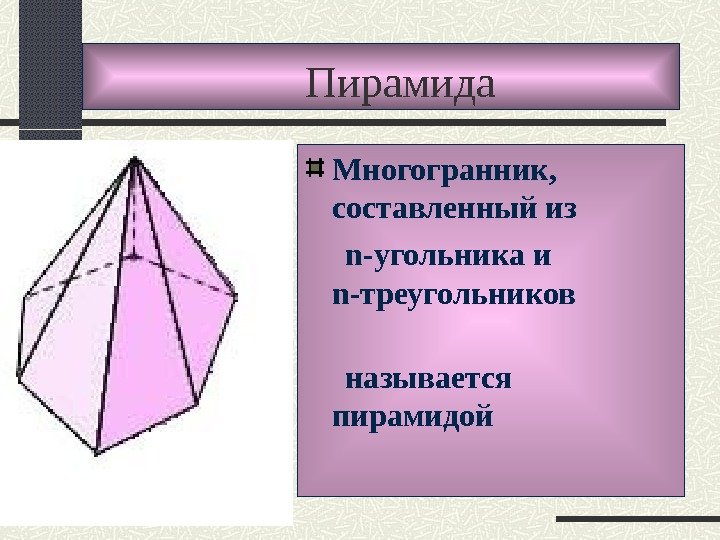
 Пирамида Многогранник, составленный из n- угольника и n- треугольников называется пирамидой
Пирамида Многогранник, составленный из n- угольника и n- треугольников называется пирамидой
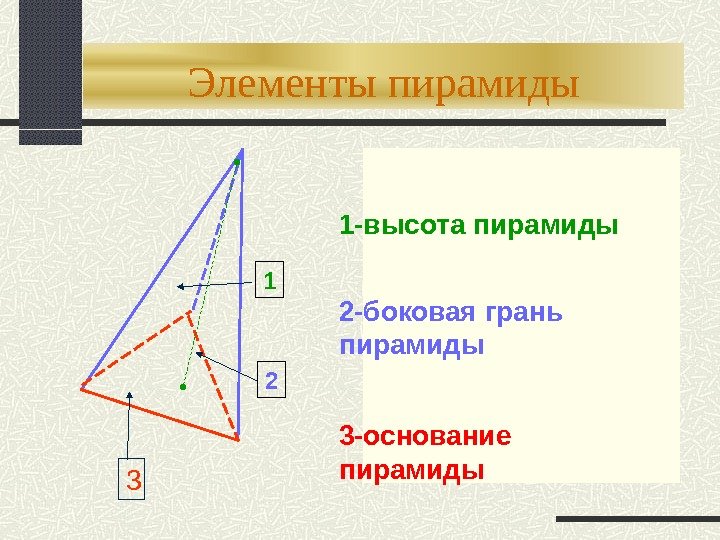
 Элементы пирамиды 1 2 3 1 -высота пирамиды 2 -боковая грань пирамиды 3 -основание пирамиды
Элементы пирамиды 1 2 3 1 -высота пирамиды 2 -боковая грань пирамиды 3 -основание пирамиды
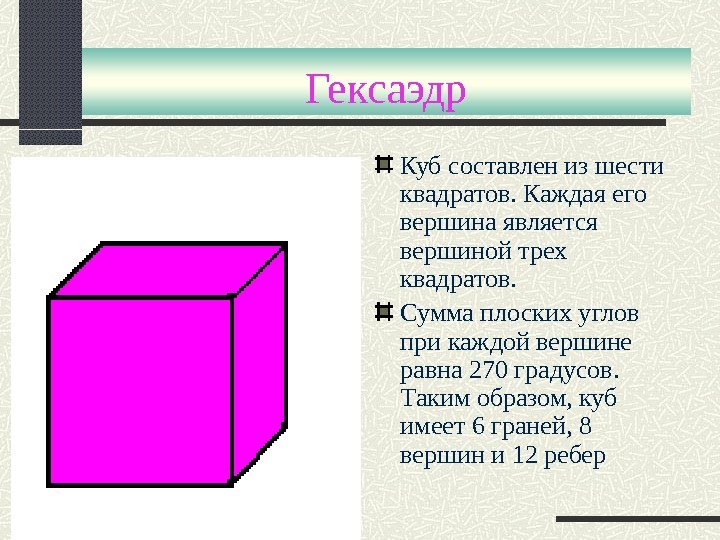
 Гексаэдр Куб составлен из шести квадратов. Каждая его вершина является вершиной трех квадратов. Сумма плоских углов при каждой вершине равна 270 градусов. Таким образом, куб имеет 6 граней, 8 вершин и 12 ребер
Гексаэдр Куб составлен из шести квадратов. Каждая его вершина является вершиной трех квадратов. Сумма плоских углов при каждой вершине равна 270 градусов. Таким образом, куб имеет 6 граней, 8 вершин и 12 ребер
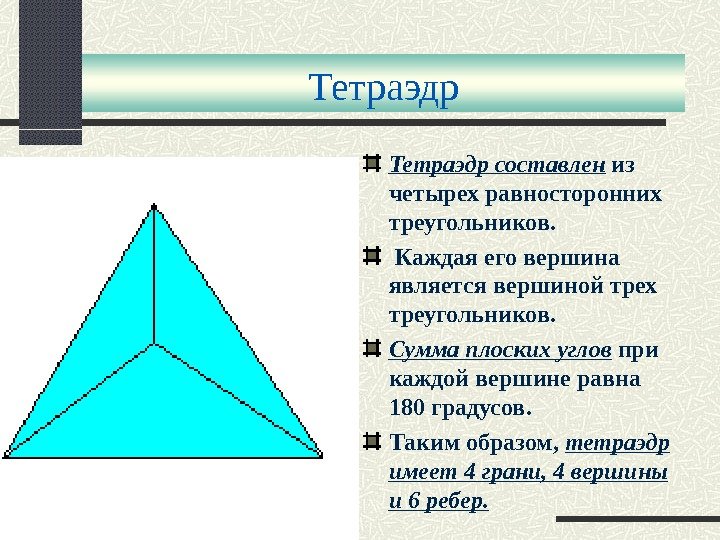
 Тетраэдр составлен из четырех равносторонних треугольников. Каждая его вершина является вершиной трех треугольников. Сумма плоских углов при каждой вершине равна 180 градусов. Таким образом, тетраэдр имеет 4 грани, 4 вершины и 6 ребер.
Тетраэдр составлен из четырех равносторонних треугольников. Каждая его вершина является вершиной трех треугольников. Сумма плоских углов при каждой вершине равна 180 градусов. Таким образом, тетраэдр имеет 4 грани, 4 вершины и 6 ребер.
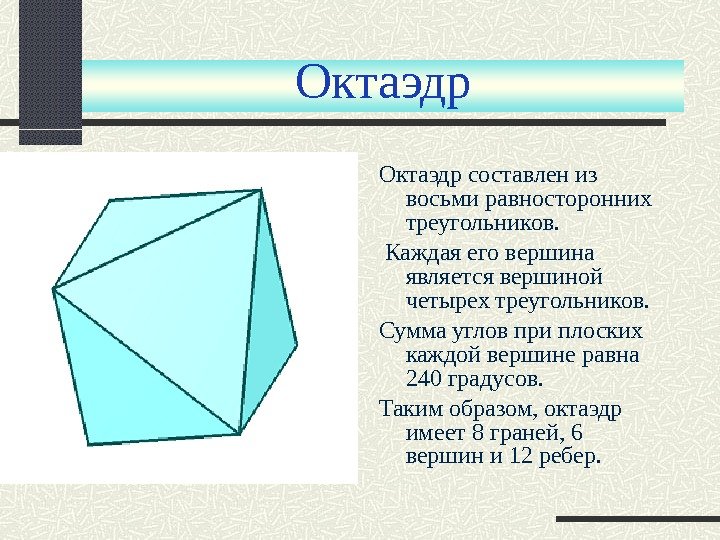
 Октаэдр составлен из восьми равносторонних треугольников. Каждая его вершина является вершиной четырех треугольников. Сумма углов при плоских каждой вершине равна 240 градусов. Таким образом, октаэдр имеет 8 граней, 6 вершин и 12 ребер.
Октаэдр составлен из восьми равносторонних треугольников. Каждая его вершина является вершиной четырех треугольников. Сумма углов при плоских каждой вершине равна 240 градусов. Таким образом, октаэдр имеет 8 граней, 6 вершин и 12 ребер.
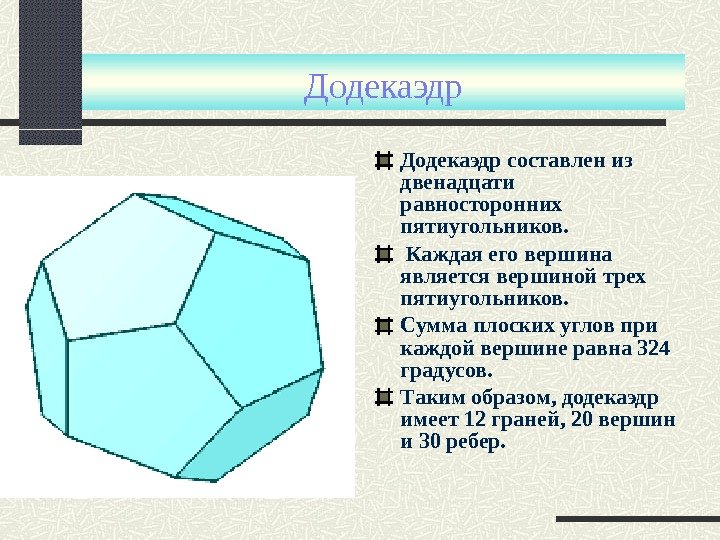
 Додекаэдр составлен из двенадцати равносторонних пятиугольников. Каждая его вершина является вершиной трех пятиугольников. Сумма плоских углов при каждой вершине равна 324 градусов. Таким образом, додекаэдр имеет 12 граней, 20 вершин и 30 ребер.
Додекаэдр составлен из двенадцати равносторонних пятиугольников. Каждая его вершина является вершиной трех пятиугольников. Сумма плоских углов при каждой вершине равна 324 градусов. Таким образом, додекаэдр имеет 12 граней, 20 вершин и 30 ребер.
 Икосаэдр составлен из двадцати равносторонних треугольников. Каждая его вершина является вершиной пяти треугольников. Сумма плоских углов при каждой вершине равна 300 градусов. Таким образом икосаэдр имеет 20 граней, 12 вершин и 30 ребер.
Икосаэдр составлен из двадцати равносторонних треугольников. Каждая его вершина является вершиной пяти треугольников. Сумма плоских углов при каждой вершине равна 300 градусов. Таким образом икосаэдр имеет 20 граней, 12 вершин и 30 ребер.
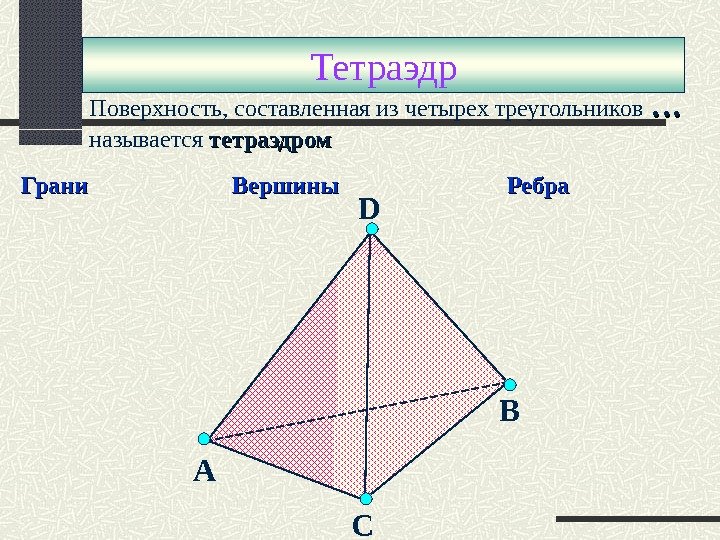
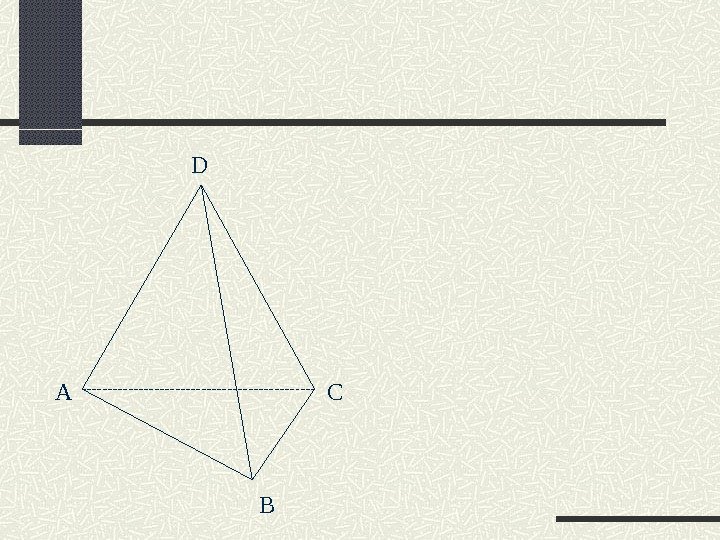
 D А С ВПоверхность, составленная из четырех треугольников …… называется тетраэдром Грани Вершины Ребра Тетраэдр
D А С ВПоверхность, составленная из четырех треугольников …… называется тетраэдром Грани Вершины Ребра Тетраэдр
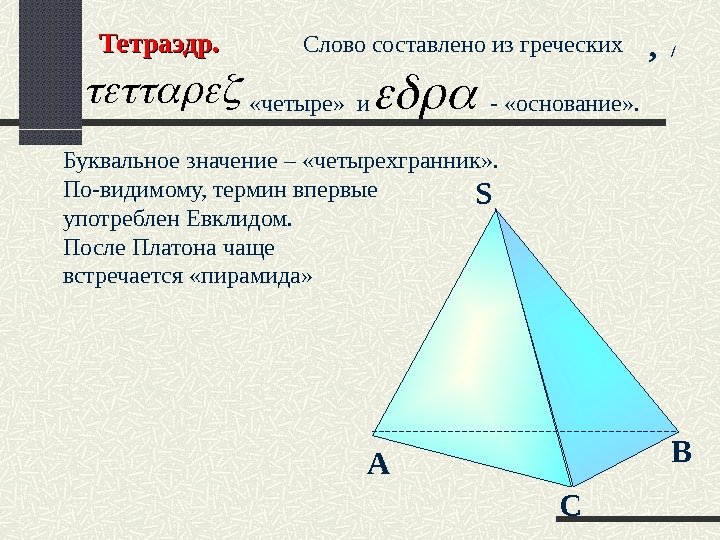
 Тетраэдр. Слово составлено из греческих «четыре» и — «основание» . Буквальное значение – «четырехгранник» . По-видимому, термин впервые употреблен Евклидом. После Платона чаще встречается «пирамида» , / СА ВS S
Тетраэдр. Слово составлено из греческих «четыре» и — «основание» . Буквальное значение – «четырехгранник» . По-видимому, термин впервые употреблен Евклидом. После Платона чаще встречается «пирамида» , / СА ВS S
 D А С ВПротивоположные ребраоснование А СВD основание
D А С ВПротивоположные ребраоснование А СВD основание
 А В СDА 1 D 1 С 1 B 1 Диагональ параллелепипеда — отрезок, соединяющий противоположные вершины.
А В СDА 1 D 1 С 1 B 1 Диагональ параллелепипеда — отрезок, соединяющий противоположные вершины.
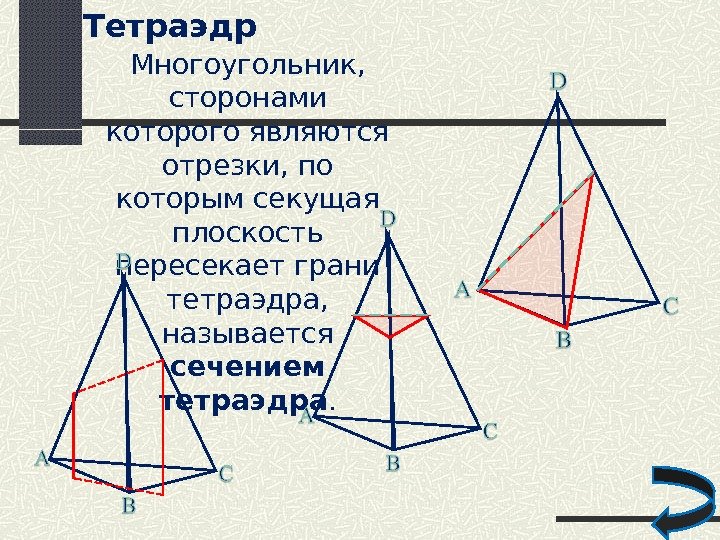
 Тетраэдр Многоугольник, сторонами которого являются отрезки, по которым секущая плоскость пересекает грани тетраэдра, называется сечением тетраэдра.
Тетраэдр Многоугольник, сторонами которого являются отрезки, по которым секущая плоскость пересекает грани тетраэдра, называется сечением тетраэдра.
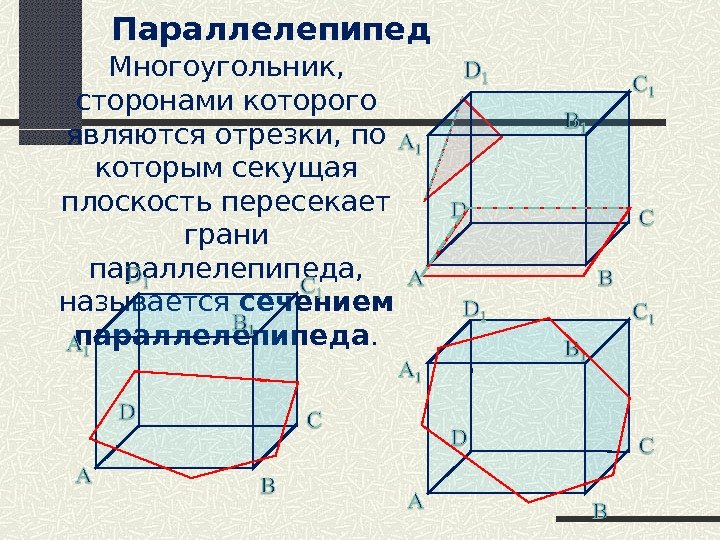
 Параллелепипед Многоугольник, сторонами которого являются отрезки, по которым секущая плоскость пересекает грани параллелепипеда, называется сечением параллелепипеда.
Параллелепипед Многоугольник, сторонами которого являются отрезки, по которым секущая плоскость пересекает грани параллелепипеда, называется сечением параллелепипеда.
 Сечение тетраэдра Т. к. тетраэдр имеет четыре грани, то его сечениями могут быть только треугольники и четырёхугольники.
Сечение тетраэдра Т. к. тетраэдр имеет четыре грани, то его сечениями могут быть только треугольники и четырёхугольники.
 Правила построения сечений ТЕТРАЭДРА а)Проводим прямые через точки, лежащие в одной плоскости; б) Ищем прямые пересечения плоскости сечения с гранями многогранника, для этого: — ищем точки пересечения прямой принадлежащей плоскости сечения с прямой, принадлежащей одной из граней (лежащие в одной плоскости); — параллельные грани плоскость сечения пересекает по параллельным прямым.
Правила построения сечений ТЕТРАЭДРА а)Проводим прямые через точки, лежащие в одной плоскости; б) Ищем прямые пересечения плоскости сечения с гранями многогранника, для этого: — ищем точки пересечения прямой принадлежащей плоскости сечения с прямой, принадлежащей одной из граней (лежащие в одной плоскости); — параллельные грани плоскость сечения пересекает по параллельным прямым.
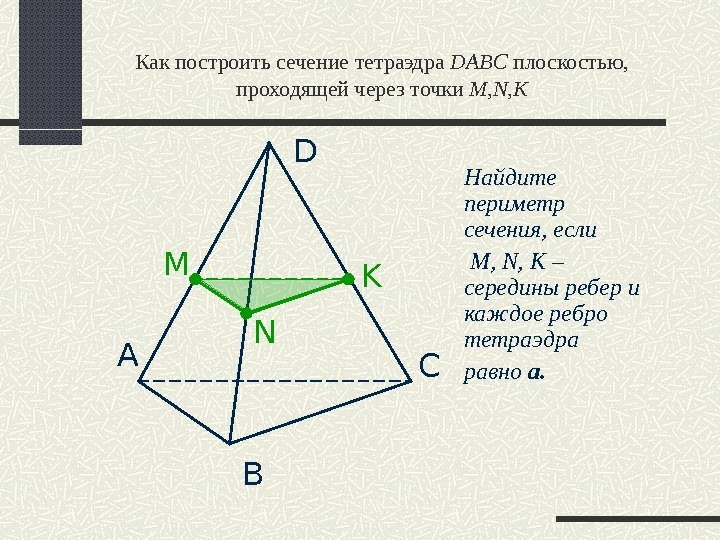
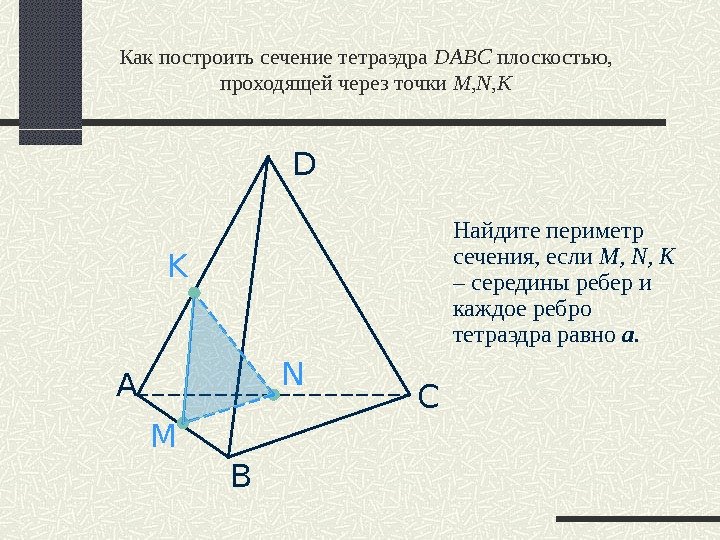
 А B D CNM KКак построить сечение тетраэдра DABC плоскостью, проходящей через точки M, N, K Найдите периметр сечения, если M, N, K – середины ребер и каждое ребро тетраэдра равно а.
А B D CNM KКак построить сечение тетраэдра DABC плоскостью, проходящей через точки M, N, K Найдите периметр сечения, если M, N, K – середины ребер и каждое ребро тетраэдра равно а.
 А B D CN M KКак построить сечение тетраэдра DABC плоскостью, проходящей через точки M, N, K Найдите периметр сечения, если M, N, K – середины ребер и каждое ребро тетраэдра равно а.
А B D CN M KКак построить сечение тетраэдра DABC плоскостью, проходящей через точки M, N, K Найдите периметр сечения, если M, N, K – середины ребер и каждое ребро тетраэдра равно а.
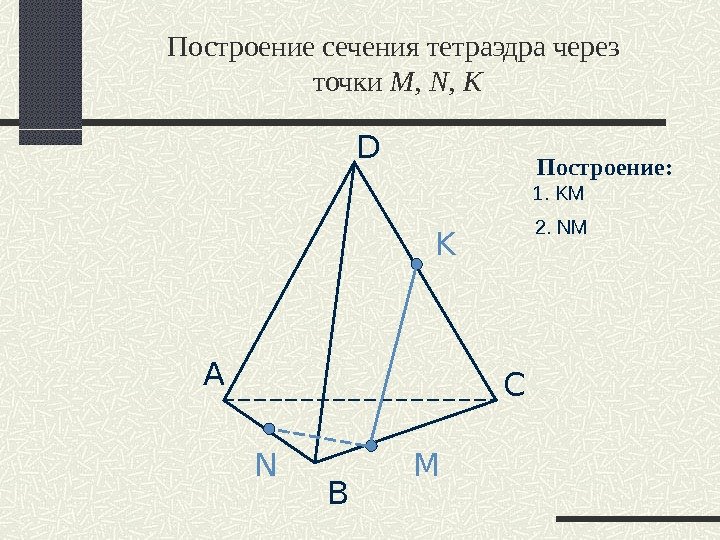
 Построение сечения тетраэдра через точки M, N, K А B D C N M K Построение: 1. KM 2. NM
Построение сечения тетраэдра через точки M, N, K А B D C N M K Построение: 1. KM 2. NM
 Построение сечения тетраэдра через точки M, N, K А B D C N M K F Построение: 3. NM ∩ АС =
Построение сечения тетраэдра через точки M, N, K А B D C N M K F Построение: 3. NM ∩ АС =
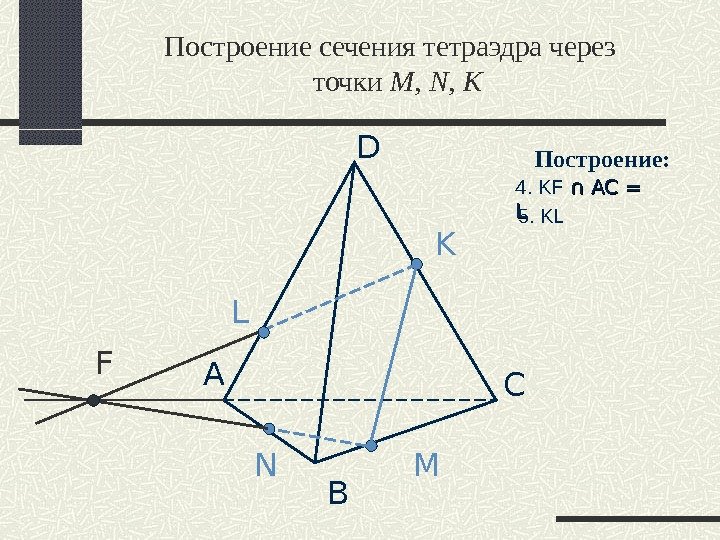
 Построение сечения тетраэдра через точки M, N, K А B D C N M K L F Построение: 4. KF ∩ АС = LL 5. KL
Построение сечения тетраэдра через точки M, N, K А B D C N M K L F Построение: 4. KF ∩ АС = LL 5. KL
 Построение сечения тетраэдра через точки M, N, K А B D C N M K L F Построение: 1. KM 2. NM 3. NM ∩ АС = FF 4. KF ∩ АС = LL 5. KL 6. LN 7. KLNM – искомое сечение
Построение сечения тетраэдра через точки M, N, K А B D C N M K L F Построение: 1. KM 2. NM 3. NM ∩ АС = FF 4. KF ∩ АС = LL 5. KL 6. LN 7. KLNM – искомое сечение
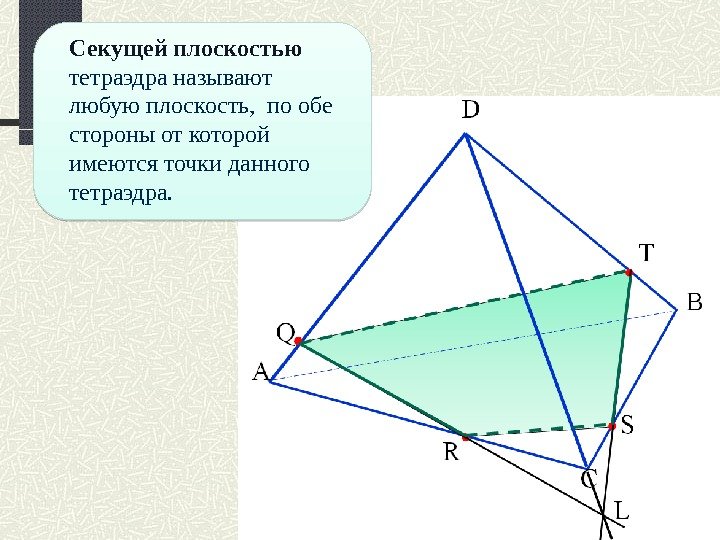
 Секущей плоскостью тетраэдра называют любую плоскость, по обе стороны от которой имеются точки данного тетраэдра.
Секущей плоскостью тетраэдра называют любую плоскость, по обе стороны от которой имеются точки данного тетраэдра.
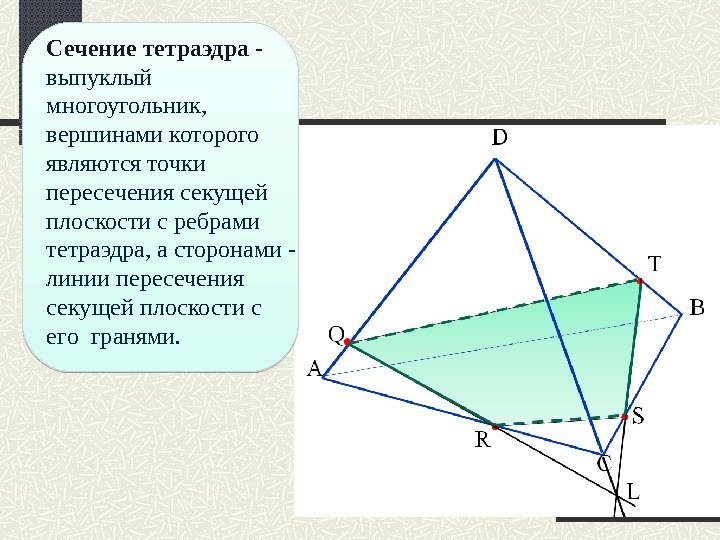
 Сечение тетраэдра — выпуклый многоугольник, вершинами которого являются точки пересечения секущей плоскости с ребрами тетраэдра, а сторонами — линии пересечения секущей плоскости с его гранями.
Сечение тетраэдра — выпуклый многоугольник, вершинами которого являются точки пересечения секущей плоскости с ребрами тетраэдра, а сторонами — линии пересечения секущей плоскости с его гранями.
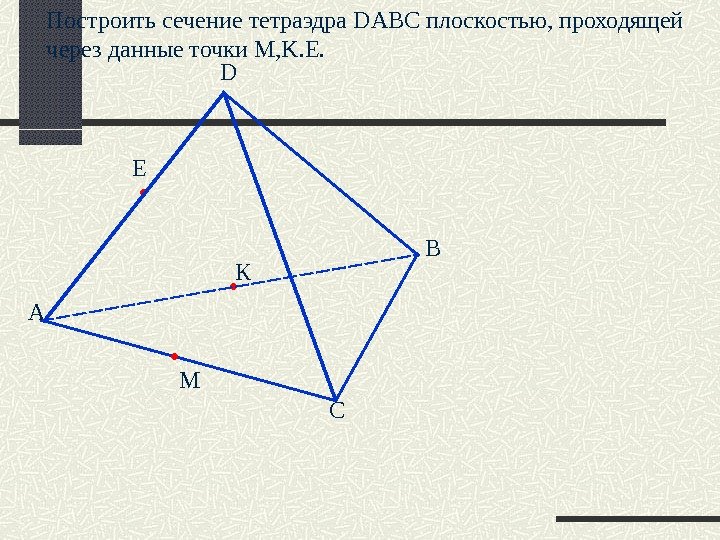
 Построить сечение тетраэдра DABC плоскостью, проходящей через данные точки M, K. E. А D B CЕ М К
Построить сечение тетраэдра DABC плоскостью, проходящей через данные точки M, K. E. А D B CЕ М К
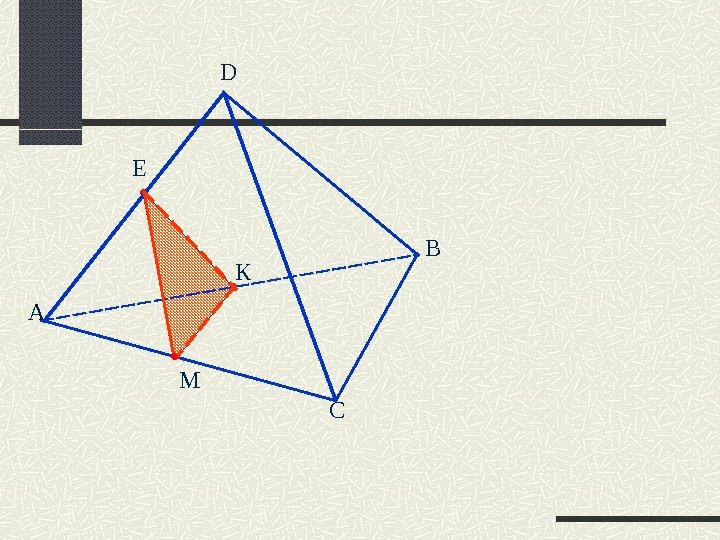
 А D B CЕ М К
А D B CЕ М К
 c. Построить сечение тетраэдра DABC плоскостью, проходящей через точку M, параллельно грани ВС D. А D B CМN P
c. Построить сечение тетраэдра DABC плоскостью, проходящей через точку M, параллельно грани ВС D. А D B CМN P
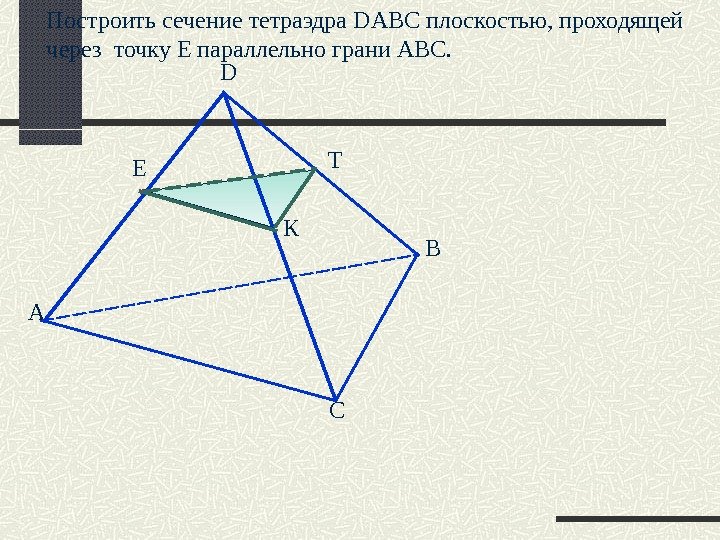
 Построить сечение тетраэдра DABC плоскостью, проходящей через точку Е параллельно грани АВС. А D B CЕ К Т
Построить сечение тетраэдра DABC плоскостью, проходящей через точку Е параллельно грани АВС. А D B CЕ К Т
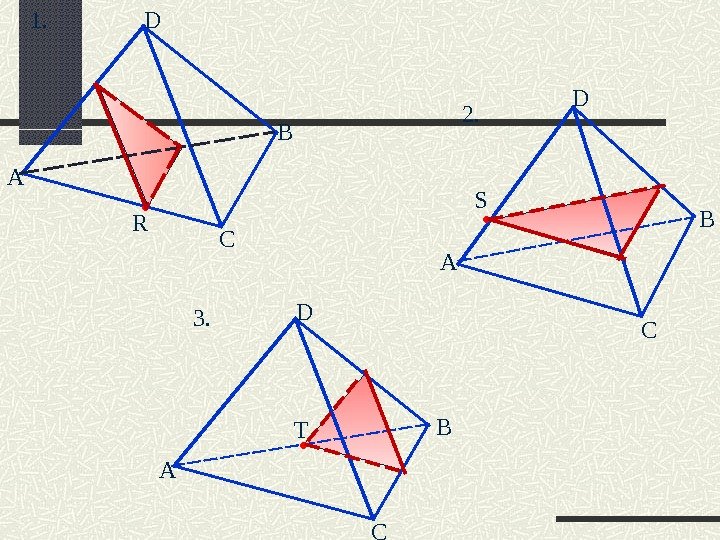
 Задание 1. Построить сечение тетраэдра ABCD , проходящее через точку R параллельно грани BCD. 2. Построить сечение тетраэдра ABCD , проходящее через точку S параллельно грани ABC. 3. Построить сечение тетраэдра ABCD , проходящее через точку T параллельно грани ACD.
Задание 1. Построить сечение тетраэдра ABCD , проходящее через точку R параллельно грани BCD. 2. Построить сечение тетраэдра ABCD , проходящее через точку S параллельно грани ABC. 3. Построить сечение тетраэдра ABCD , проходящее через точку T параллельно грани ACD.
 А D B C S 2. А D B C R 1. А D B CT 3.
А D B C S 2. А D B C R 1. А D B CT 3.
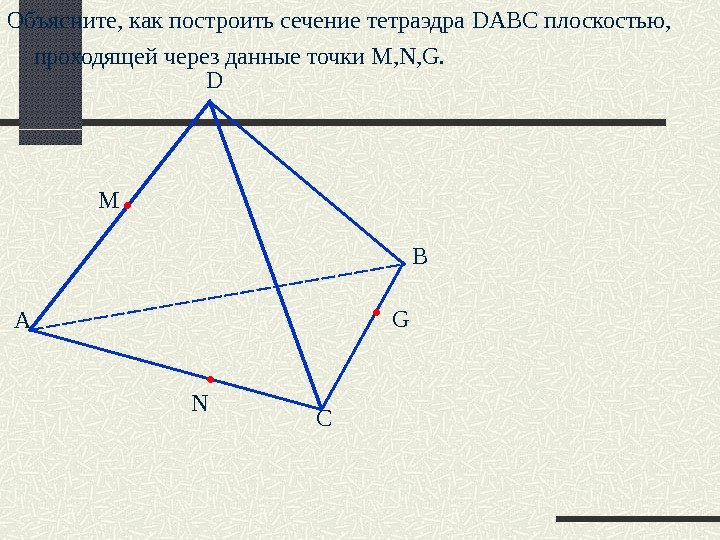
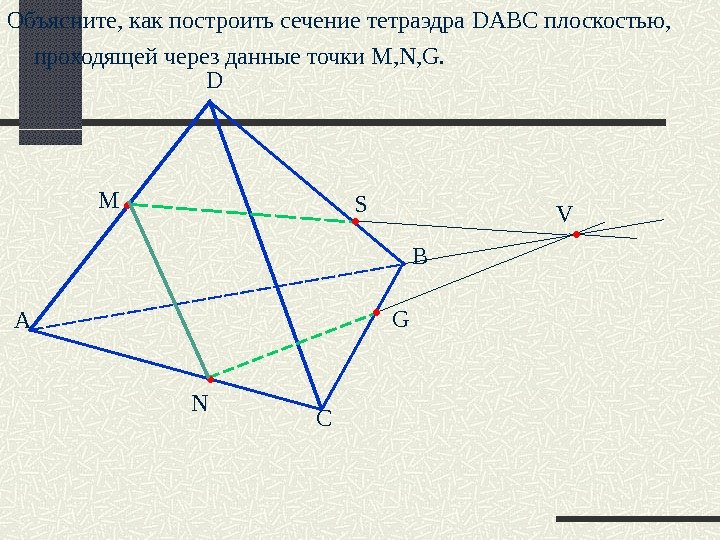
 А D B CNM GОбъясните, как построить сечение тетраэдра DABC плоскостью, проходящей через данные точки M, N, G.
А D B CNM GОбъясните, как построить сечение тетраэдра DABC плоскостью, проходящей через данные точки M, N, G.
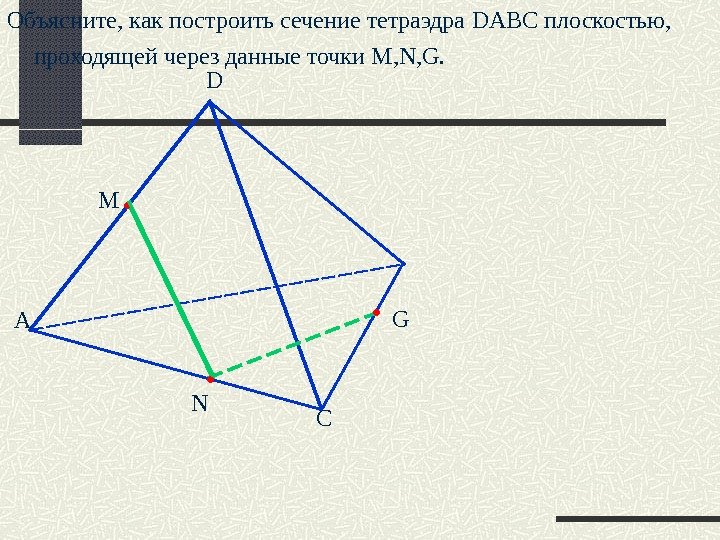
 А D CNM GОбъясните, как построить сечение тетраэдра DABC плоскостью, проходящей через данные точки M, N, G.
А D CNM GОбъясните, как построить сечение тетраэдра DABC плоскостью, проходящей через данные точки M, N, G.
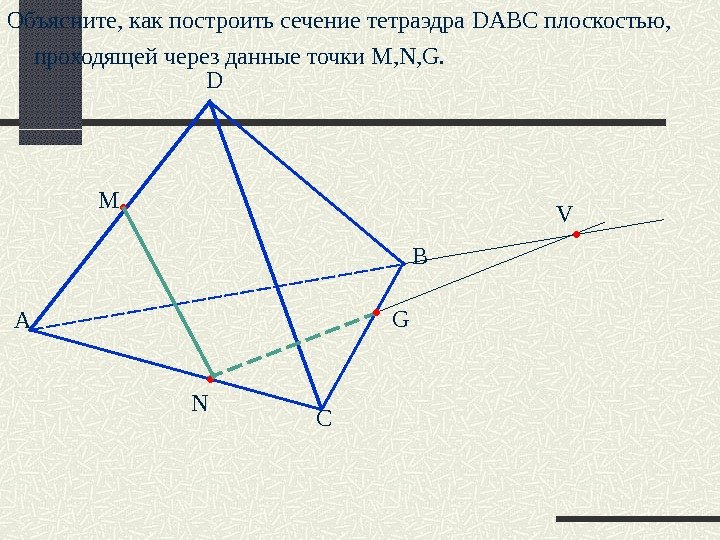
 А D B CNM V GОбъясните, как построить сечение тетраэдра DABC плоскостью, проходящей через данные точки M, N, G.
А D B CNM V GОбъясните, как построить сечение тетраэдра DABC плоскостью, проходящей через данные точки M, N, G.
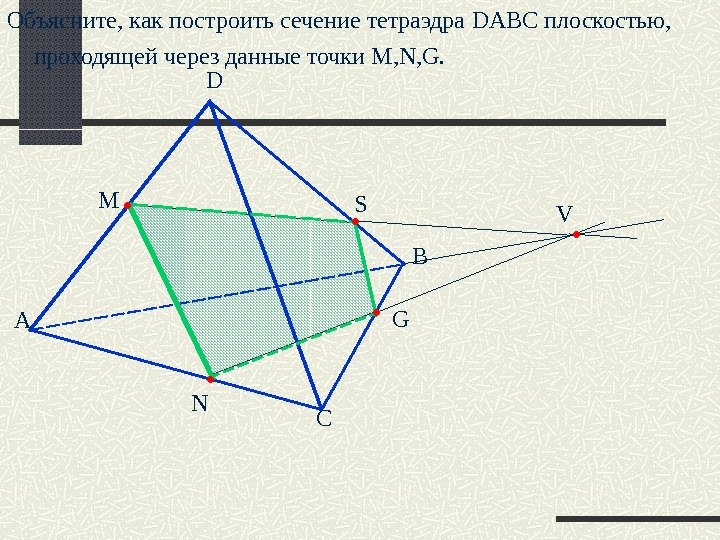
 А D B CNM S V GОбъясните, как построить сечение тетраэдра DABC плоскостью, проходящей через данные точки M, N, G.
А D B CNM S V GОбъясните, как построить сечение тетраэдра DABC плоскостью, проходящей через данные точки M, N, G.
 А D B CNM S V GОбъясните, как построить сечение тетраэдра DABC плоскостью, проходящей через данные точки M, N, G.
А D B CNM S V GОбъясните, как построить сечение тетраэдра DABC плоскостью, проходящей через данные точки M, N, G.
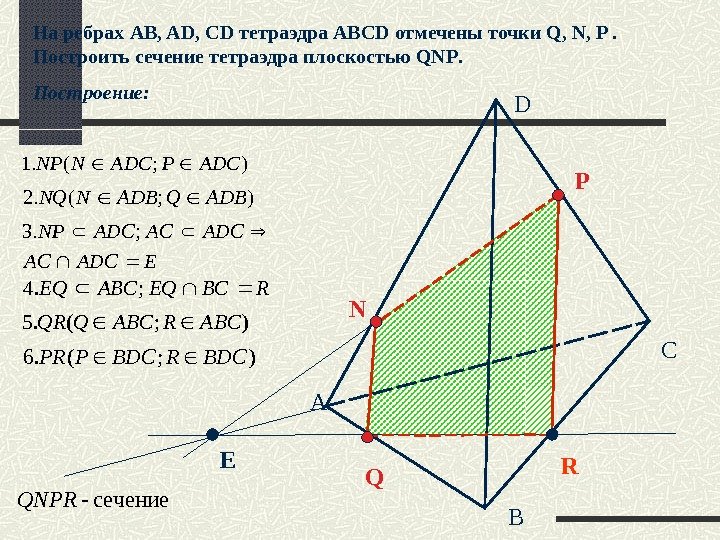
 А С В D N P Q); (. 1 ADCPADCNNP); (. 2 ADBQADBNNQ EADCACADCNP ; . 3 RBCEQABCEQ; . 4 RНа ребрах AB, AD, CD тетраэдра ABCD отмечены точки Q, N, P . Построить сечение тетраэдра плоскостью QNP. Построение: ); (. 5 ABCRABCQQR ); (. 6 BDCRBDCPPR сечение-QNPR
А С В D N P Q); (. 1 ADCPADCNNP); (. 2 ADBQADBNNQ EADCACADCNP ; . 3 RBCEQABCEQ; . 4 RНа ребрах AB, AD, CD тетраэдра ABCD отмечены точки Q, N, P . Построить сечение тетраэдра плоскостью QNP. Построение: ); (. 5 ABCRABCQQR ); (. 6 BDCRBDCPPR сечение-QNPR
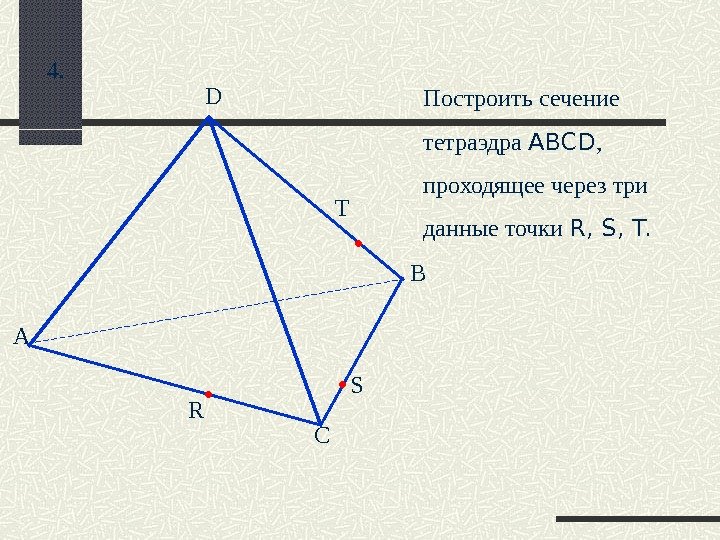
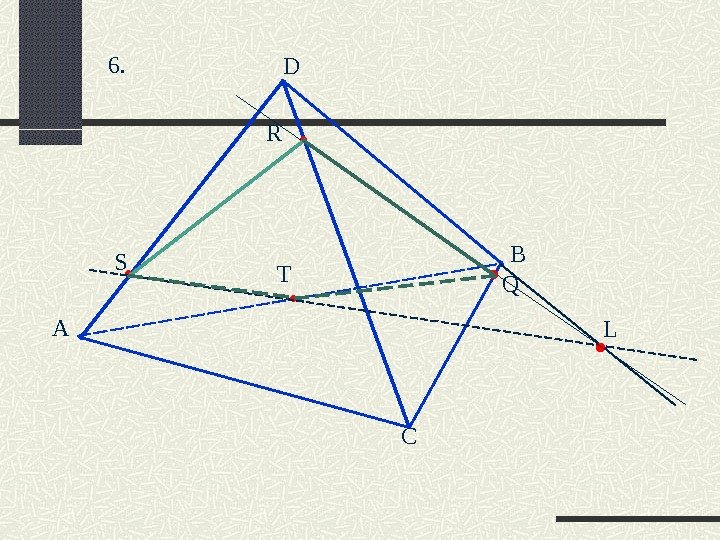
 А D B C R T S 4. Построить сечение тетраэдра ABCD , проходящее через три данные точки R, S, T.
А D B C R T S 4. Построить сечение тетраэдра ABCD , проходящее через три данные точки R, S, T.
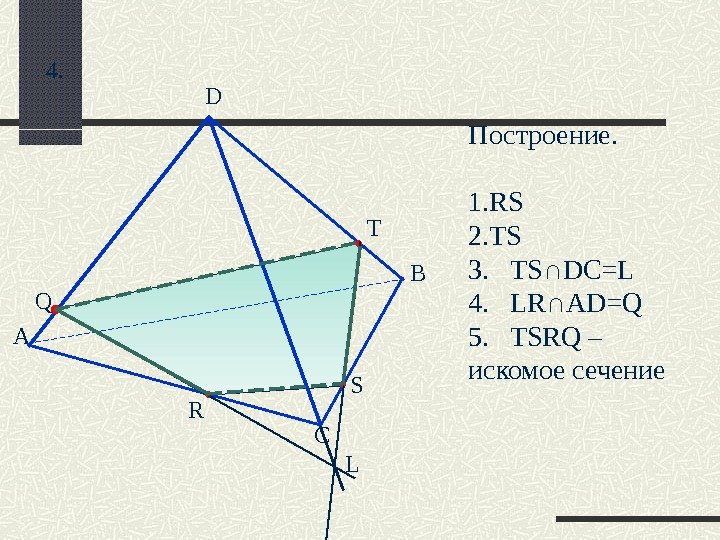
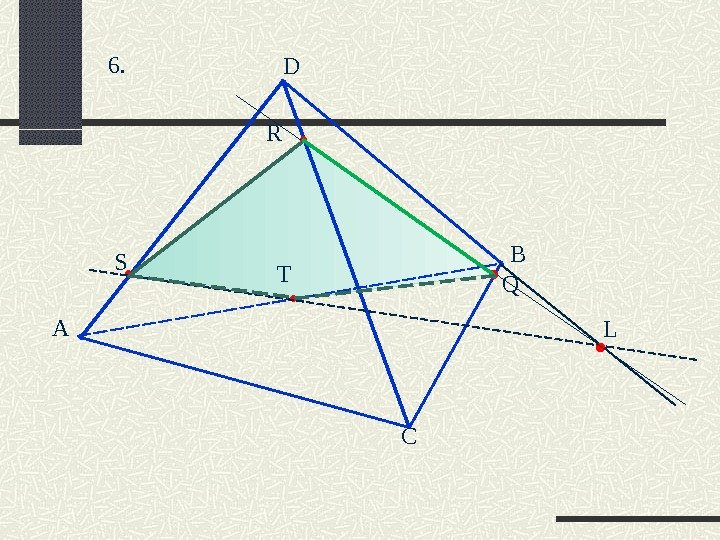
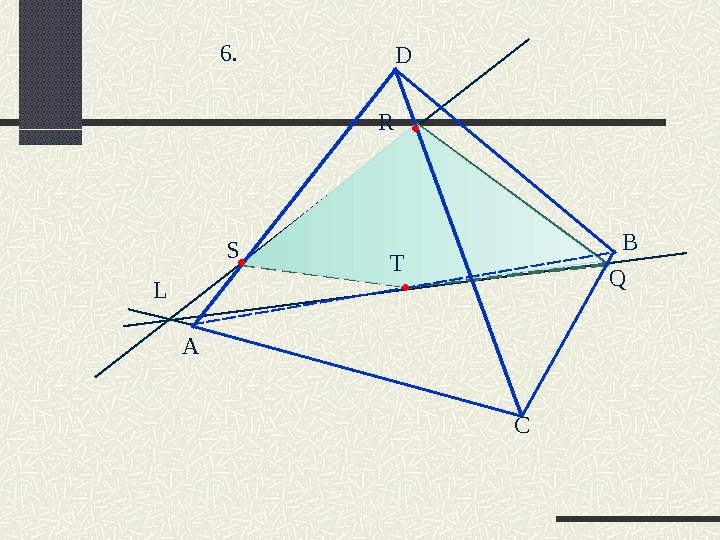
 А D B C R T S . Q L Построение. 1. RS 2. TS 3. TS∩DC=L 4. LR∩AD=Q 5. TSRQ – искомое сечение 4.
А D B C R T S . Q L Построение. 1. RS 2. TS 3. TS∩DC=L 4. LR∩AD=Q 5. TSRQ – искомое сечение 4.
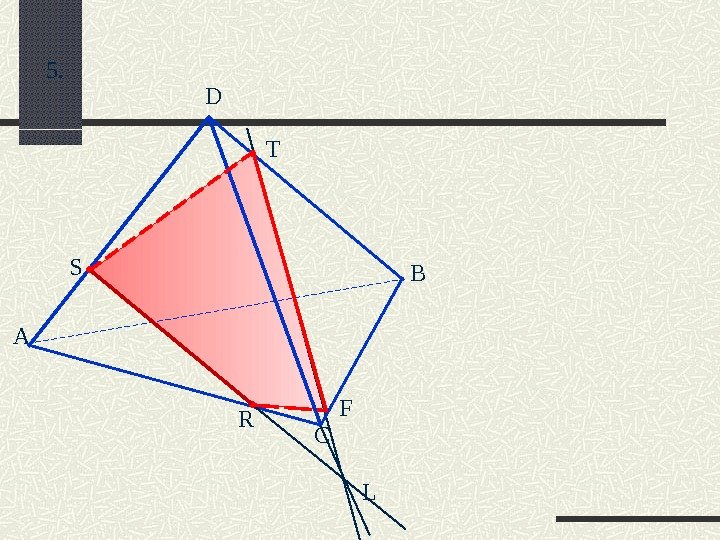
 А D B C R T S 5. L
А D B C R T S 5. L
 А D B C R T S 5. . F. L
А D B C R T S 5. . F. L
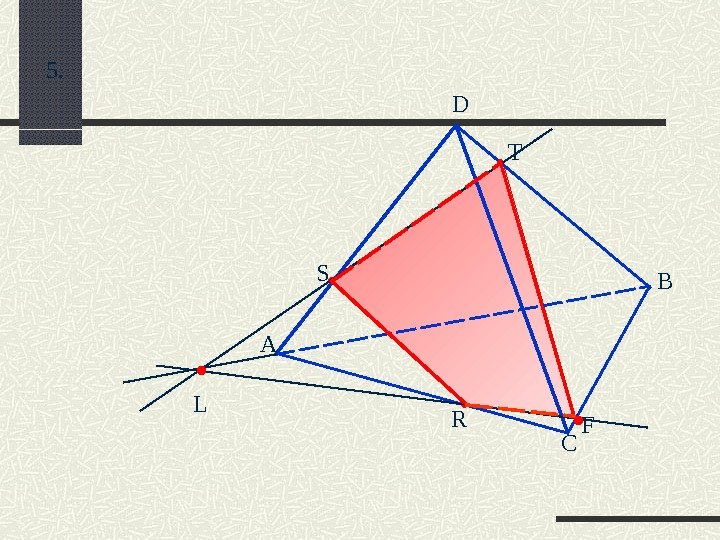
 А D B C TS 6. L. Q. R
А D B C TS 6. L. Q. R
 А D B C R TS 6. . L. Q
А D B C R TS 6. . L. Q
 А D B C R TS 6. . L. Q
А D B C R TS 6. . L. Q
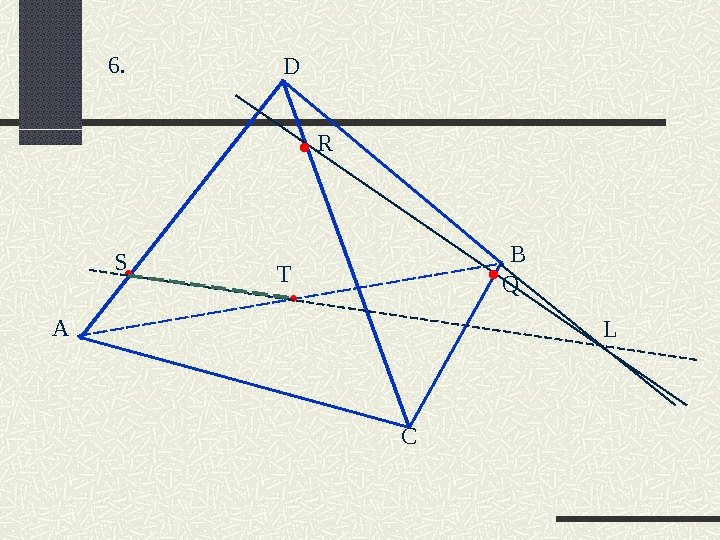
 L А D B C R TS 6. Q
L А D B C R TS 6. Q




 Индивидуальное задание Построить сечение тетраэдра по данным точкам
Индивидуальное задание Построить сечение тетраэдра по данным точкам
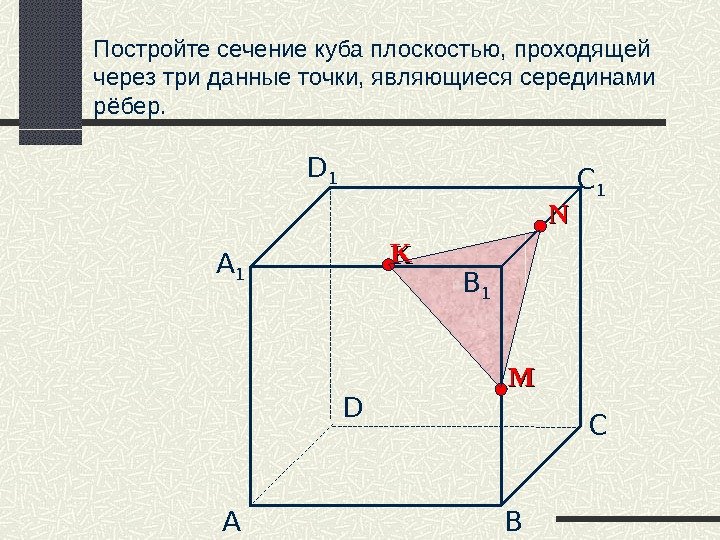
 Постройте сечение куба плоскостью, проходящей через три данные точки, являющиеся серединами рёбер. А B СDD 1 С 1 B 1 А 1 MMKK NN
Постройте сечение куба плоскостью, проходящей через три данные точки, являющиеся серединами рёбер. А B СDD 1 С 1 B 1 А 1 MMKK NN
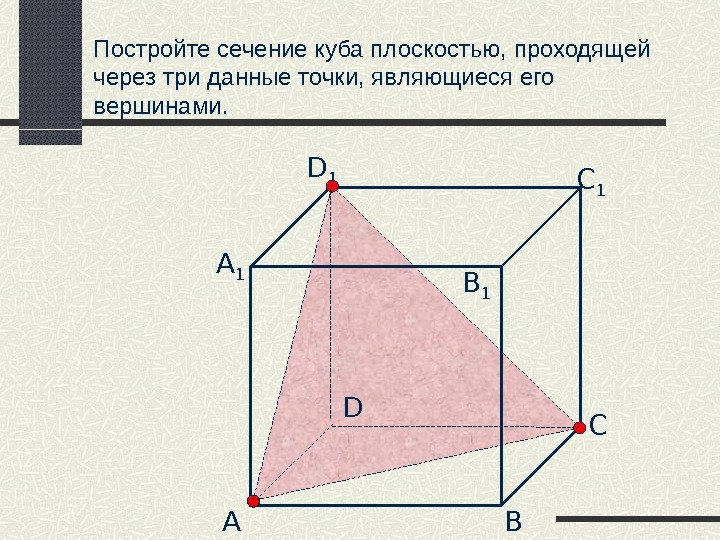
 Постройте сечение куба плоскостью, проходящей через три данные точки, являющиеся его вершинами. А B СDD 1 С 1 B 1 А
Постройте сечение куба плоскостью, проходящей через три данные точки, являющиеся его вершинами. А B СDD 1 С 1 B 1 А
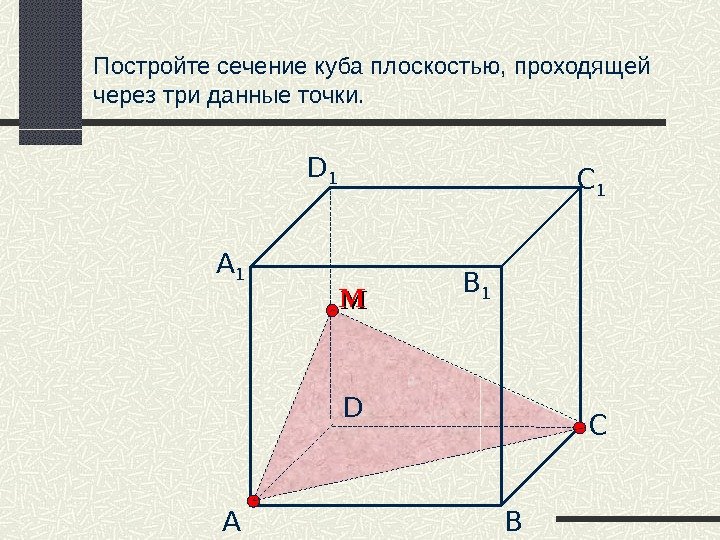
 Постройте сечение куба плоскостью, проходящей через три данные точки. А B СDD 1 С 1 B 1 А 1 ММ
Постройте сечение куба плоскостью, проходящей через три данные точки. А B СDD 1 С 1 B 1 А 1 ММ
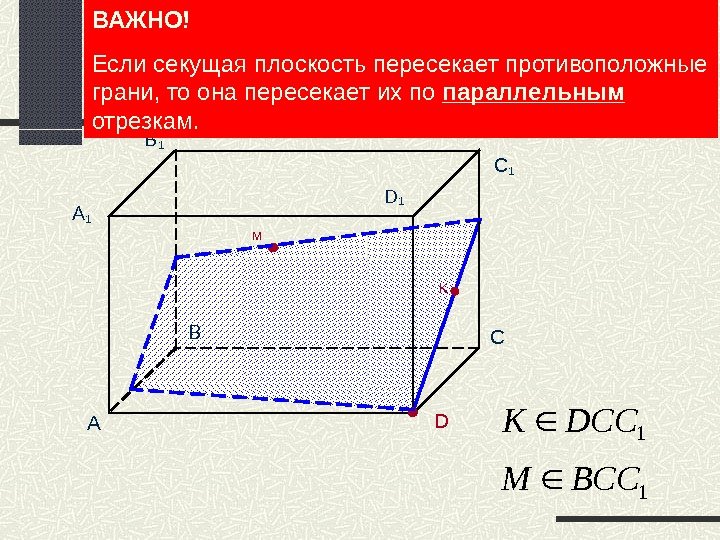
 A B СB 1 D KM C 1 A 11 DCCK 1 BCCM ВАЖНО! Если секущая плоскость пересекает противоположные грани, то она пересекает их по параллельным отрезкам.
A B СB 1 D KM C 1 A 11 DCCK 1 BCCM ВАЖНО! Если секущая плоскость пересекает противоположные грани, то она пересекает их по параллельным отрезкам.
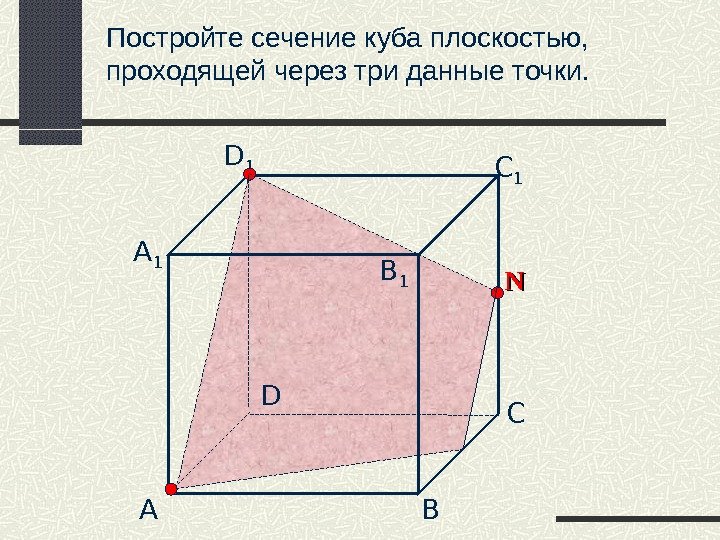
 Постройте сечение куба плоскостью, проходящей через три данные точки. А B СDD 1 С 1 B 1 А 1 NN
Постройте сечение куба плоскостью, проходящей через три данные точки. А B СDD 1 С 1 B 1 А 1 NN
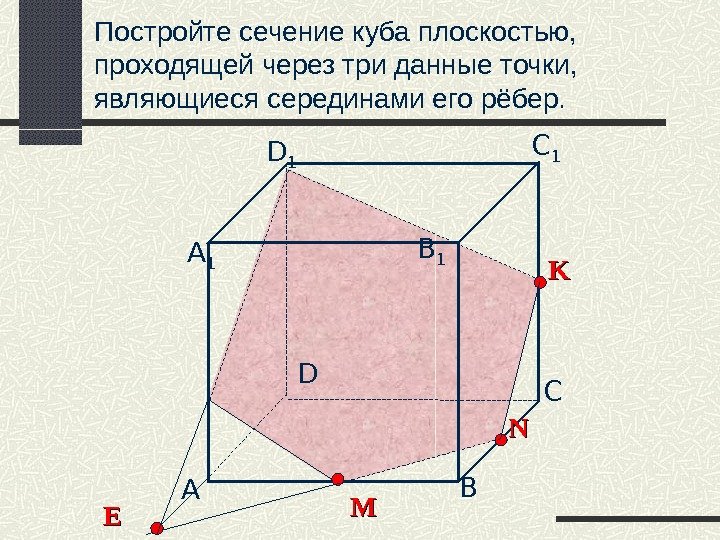
 Постройте сечение куба плоскостью, проходящей через три данные точки, являющиеся серединами его рёбер. А B СDD 1 С 1 B 1 А 1 KK NN MM ЕЕ
Постройте сечение куба плоскостью, проходящей через три данные точки, являющиеся серединами его рёбер. А B СDD 1 С 1 B 1 А 1 KK NN MM ЕЕ
 Постройте сечение куба плоскостью, проходящей через три данные точки, являющиеся серединами его рёбер. А B СDD 1 С 1 B 1 А 1 KK NN MMЕЕ
Постройте сечение куба плоскостью, проходящей через три данные точки, являющиеся серединами его рёбер. А B СDD 1 С 1 B 1 А 1 KK NN MMЕЕ
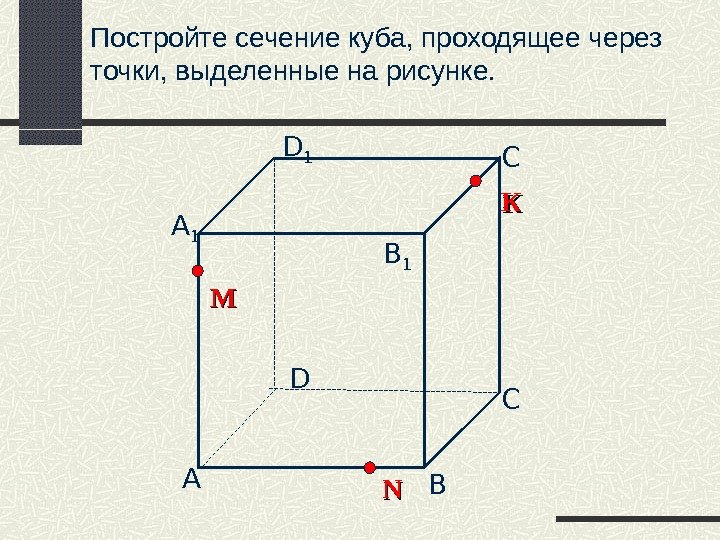
 Постройте сечение куба, проходящее через точки, выделенные на рисунке. А B СDD 1 С 1 B 1 NNMMА 1 КК
Постройте сечение куба, проходящее через точки, выделенные на рисунке. А B СDD 1 С 1 B 1 NNMMА 1 КК
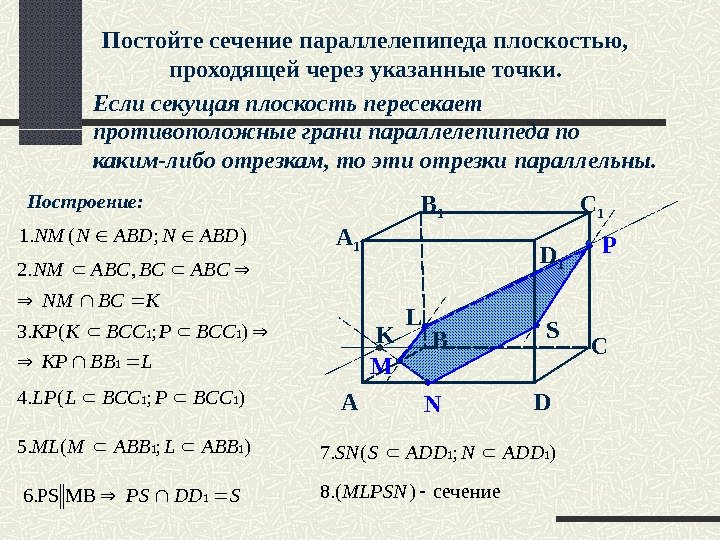
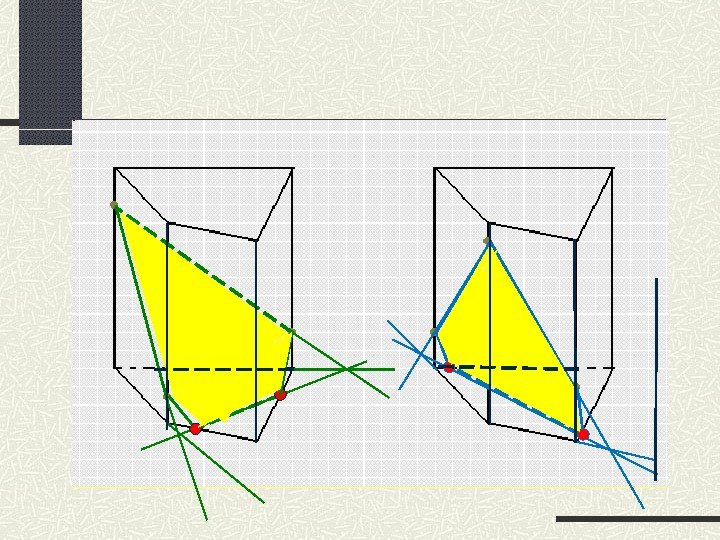
 Постойте сечение параллелепипеда плоскостью, проходящей через указанные точки. А M D СС 1 А 1 В D 1 В 1 N РЕсли секущая плоскость пересекает противоположные грани параллелепипеда по каким-либо отрезкам, то эти отрезки параллельны. SL KПостроение: ); (. 1 ABDNNM KBCNM ABCBCABCNM , . 2 LBBKP BCCPBCCKKP 1 11); (. 3 ); (. 511 ABBLABBMML ); (. 4 11 BCCPBCCLLP SDDPS 1 MBPS. 6 ); (. 7 11 ADDNADDSSN сечение). (8 MLPSN
Постойте сечение параллелепипеда плоскостью, проходящей через указанные точки. А M D СС 1 А 1 В D 1 В 1 N РЕсли секущая плоскость пересекает противоположные грани параллелепипеда по каким-либо отрезкам, то эти отрезки параллельны. SL KПостроение: ); (. 1 ABDNNM KBCNM ABCBCABCNM , . 2 LBBKP BCCPBCCKKP 1 11); (. 3 ); (. 511 ABBLABBMML ); (. 4 11 BCCPBCCLLP SDDPS 1 MBPS. 6 ); (. 7 11 ADDNADDSSN сечение). (8 MLPSN
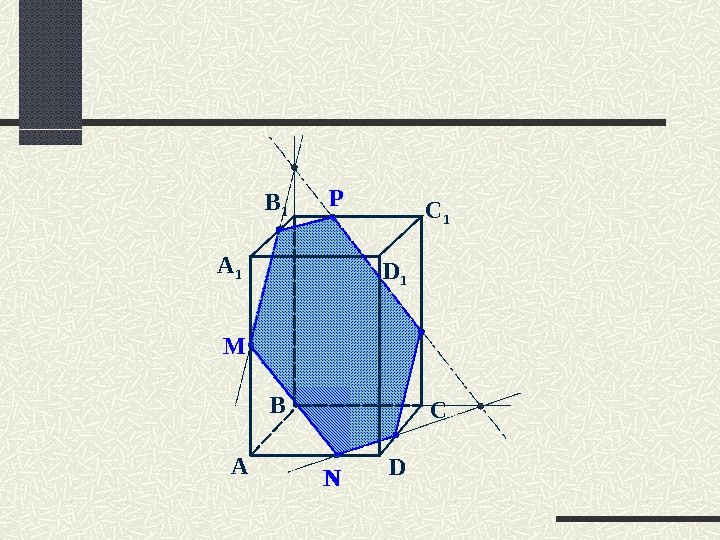
 АM D NА 1 В D 1 В 1 Р M С N С 1 В D 1 Р
АM D NА 1 В D 1 В 1 Р M С N С 1 В D 1 Р
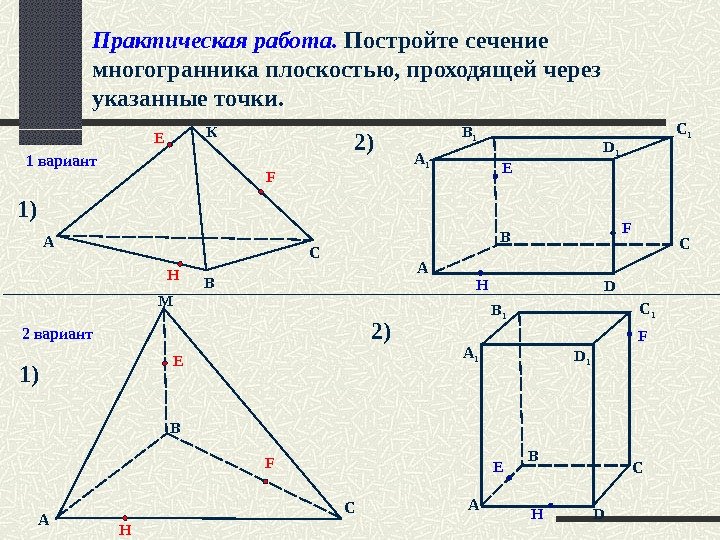
 Практическая работа. Постройте сечение многогранника плоскостью, проходящей через указанные точки. MA А 1 1) 1 ) 2 )В СК В A С A D CBA В С DB 1 С 1 D 1 C 1 B 1 A 1 D 1 E F H E H F HE FF H E 1 вариант 2 вариант
Практическая работа. Постройте сечение многогранника плоскостью, проходящей через указанные точки. MA А 1 1) 1 ) 2 )В СК В A С A D CBA В С DB 1 С 1 D 1 C 1 B 1 A 1 D 1 E F H E H F HE FF H E 1 вариант 2 вариант
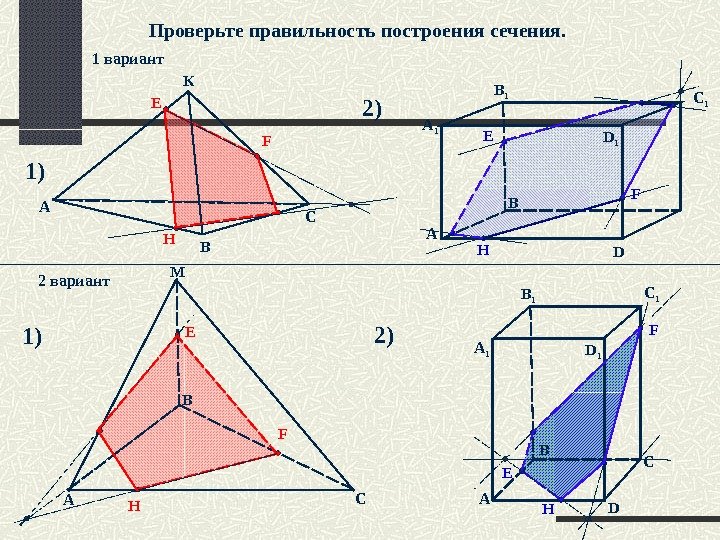
 Проверьте правильность построения сечения. MA А 1 1) 2 ) В СК В A С A D CBA В DB 1 С 1 D 1 C 1 B 1 A 1 D 1 E F H E H F HE FF H E 1 вариант 2 вариант 1) 2 )
Проверьте правильность построения сечения. MA А 1 1) 2 ) В СК В A С A D CBA В DB 1 С 1 D 1 C 1 B 1 A 1 D 1 E F H E H F HE FF H E 1 вариант 2 вариант 1) 2 )
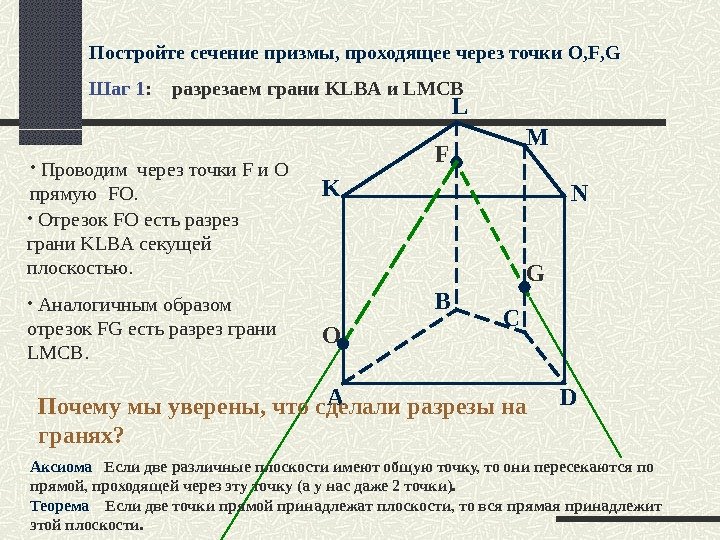
 A B C DK L M NF G • Проводим через точки F и O прямую FO. O • Отрезок FO есть разрез грани KLBA секущей плоскостью. • Аналогичным образом отрезок FG есть разрез грани LMCB. Аксиома Если две различные плоскости имеют общую точку, то они пересекаются по прямой, проходящей через эту точку (а у нас даже 2 точки). Теорема Если две точки прямой принадлежат плоскости, то вся прямая принадлежит этой плоскости. Почему мы уверены, что сделали разрезы на гранях ? Постройте сечение призмы, проходящее через точки O , F , G Шаг 1 : разрезаем грани KLBA и LM
A B C DK L M NF G • Проводим через точки F и O прямую FO. O • Отрезок FO есть разрез грани KLBA секущей плоскостью. • Аналогичным образом отрезок FG есть разрез грани LMCB. Аксиома Если две различные плоскости имеют общую точку, то они пересекаются по прямой, проходящей через эту точку (а у нас даже 2 точки). Теорема Если две точки прямой принадлежат плоскости, то вся прямая принадлежит этой плоскости. Почему мы уверены, что сделали разрезы на гранях ? Постройте сечение призмы, проходящее через точки O , F , G Шаг 1 : разрезаем грани KLBA и LM
 A B C DK L M NF G Шаг 2 : ищем след секущей плоскости на плоскости основания • Проводим прямую АВ до пересечения с прямой FO. O • Получим точку H , которая принадлежит и секущей плоскости, и плоскости основания. • Аналогичным образом получим точку R. Аксиома Если две различные плоскости имеют общую точку, то они пересекаются по прямой, проходящей через эту точку (а у нас даже 2 точки). Теорема Если две точки прямой принадлежат плоскости, то вся прямая принадлежит этой плоскости. H R • Через точки H и R проводим прямую HR – след секущей плоскости Почему мы уверены, прямая HR – след секущей плоскости на плоскости основания ?
A B C DK L M NF G Шаг 2 : ищем след секущей плоскости на плоскости основания • Проводим прямую АВ до пересечения с прямой FO. O • Получим точку H , которая принадлежит и секущей плоскости, и плоскости основания. • Аналогичным образом получим точку R. Аксиома Если две различные плоскости имеют общую точку, то они пересекаются по прямой, проходящей через эту точку (а у нас даже 2 точки). Теорема Если две точки прямой принадлежат плоскости, то вся прямая принадлежит этой плоскости. H R • Через точки H и R проводим прямую HR – след секущей плоскости Почему мы уверены, прямая HR – след секущей плоскости на плоскости основания ?
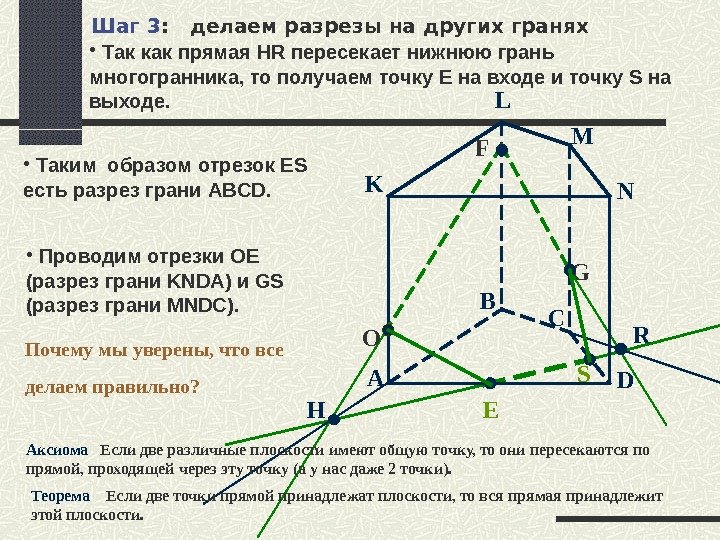
 A B C DK L M NF G O H R EШаг 3 : делаем разрезы на других гранях • Так как прямая HR пересекает нижнюю грань многогранника, то получаем точку E на входе и точку S на выходе. S • Таким образом отрезок ES есть разрез грани ABCD. • Проводим отрезки ОЕ (разрез грани KNDA ) и GS (разрез грани MNDC ). Почему мы уверены, что все делаем правильно ? Аксиома Если две различные плоскости имеют общую точку, то они пересекаются по прямой, проходящей через эту точку (а у нас даже 2 точки). Теорема Если две точки прямой принадлежат плоскости, то вся прямая принадлежит этой плоскости.
A B C DK L M NF G O H R EШаг 3 : делаем разрезы на других гранях • Так как прямая HR пересекает нижнюю грань многогранника, то получаем точку E на входе и точку S на выходе. S • Таким образом отрезок ES есть разрез грани ABCD. • Проводим отрезки ОЕ (разрез грани KNDA ) и GS (разрез грани MNDC ). Почему мы уверены, что все делаем правильно ? Аксиома Если две различные плоскости имеют общую точку, то они пересекаются по прямой, проходящей через эту точку (а у нас даже 2 точки). Теорема Если две точки прямой принадлежат плоскости, то вся прямая принадлежит этой плоскости.
 CB E S A DK L M NF GШаг 4 : выделяем сечение многогранника Все разрезы образовали пятиугольник OFGSE , который и является сечением призмы плоскостью, проходящей через точки O , F , G. O
CB E S A DK L M NF GШаг 4 : выделяем сечение многогранника Все разрезы образовали пятиугольник OFGSE , который и является сечением призмы плоскостью, проходящей через точки O , F , G. O
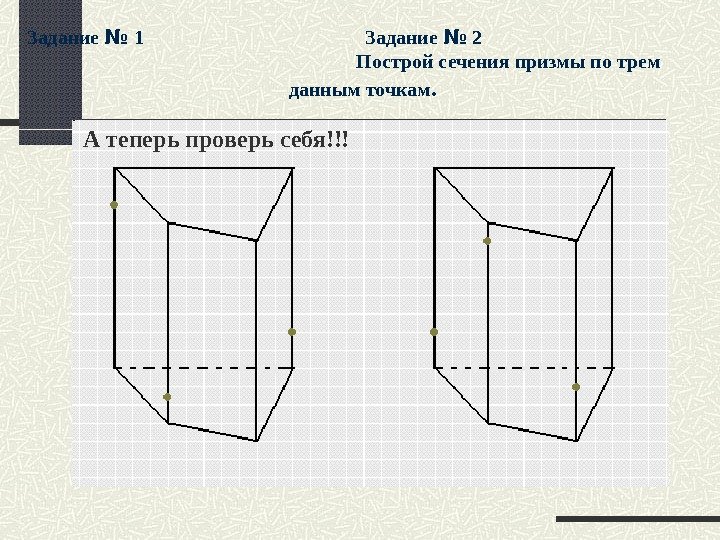
 Задание № 1 Задание № 2 Построй сечения призмы по трем данным точкам. А теперь проверь себя!!!
Задание № 1 Задание № 2 Построй сечения призмы по трем данным точкам. А теперь проверь себя!!!

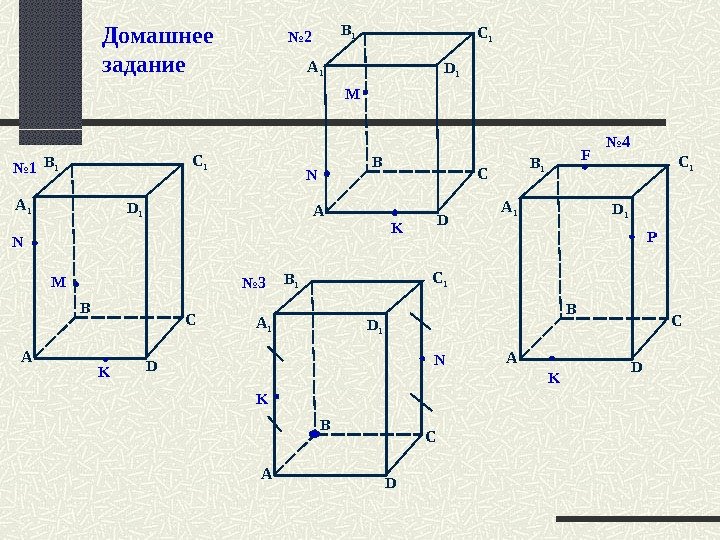
 A D CB C 1 B 1 A 1 D 1 MN K A D CB C 1 B 1 A 1 D 1 KN M A D CB C 1 B 1 A 1 D 1 Домашнее задание K N A D CB C 1 B 1 A 1 D 1 P K F№ 2 № 1 № 3 №
A D CB C 1 B 1 A 1 D 1 MN K A D CB C 1 B 1 A 1 D 1 KN M A D CB C 1 B 1 A 1 D 1 Домашнее задание K N A D CB C 1 B 1 A 1 D 1 P K F№ 2 № 1 № 3 №
 А В
А В
 Решение задач
Решение задач
 Да, путь познания не гладок. Но знайте вы со школьных лет: Загадок больше, чем разгадок. И поискам предела нет.
Да, путь познания не гладок. Но знайте вы со школьных лет: Загадок больше, чем разгадок. И поискам предела нет.
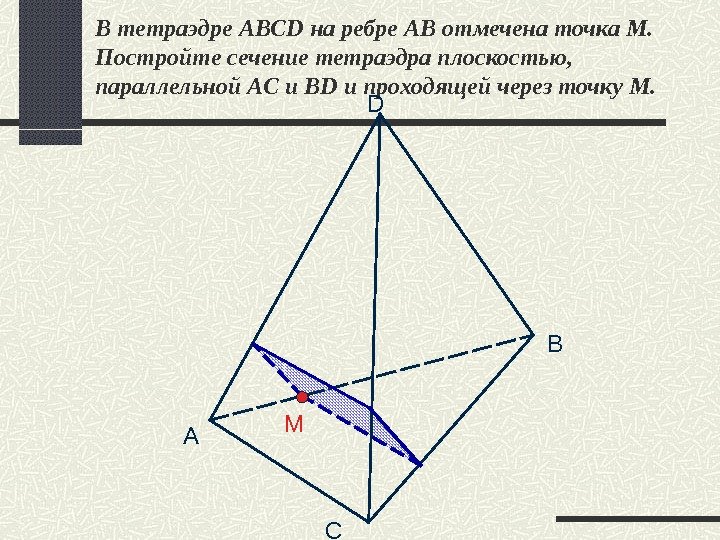
 В тетраэдре ABCD на ребре АВ отмечена точка М. Постройте сечение тетраэдра плоскостью, параллельной AC и BD и проходящей через точку М. A B C D M
В тетраэдре ABCD на ребре АВ отмечена точка М. Постройте сечение тетраэдра плоскостью, параллельной AC и BD и проходящей через точку М. A B C D M
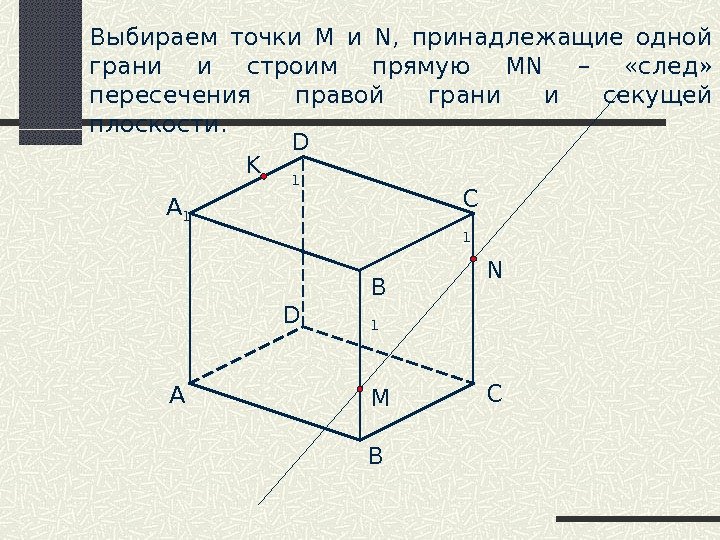
 A B CD B 1 C 1 D 1 M NKВыбираем точки М и N , принадлежащие одной грани и строим прямую MN – «след» пересечения правой грани и секущей плоскости.
A B CD B 1 C 1 D 1 M NKВыбираем точки М и N , принадлежащие одной грани и строим прямую MN – «след» пересечения правой грани и секущей плоскости.
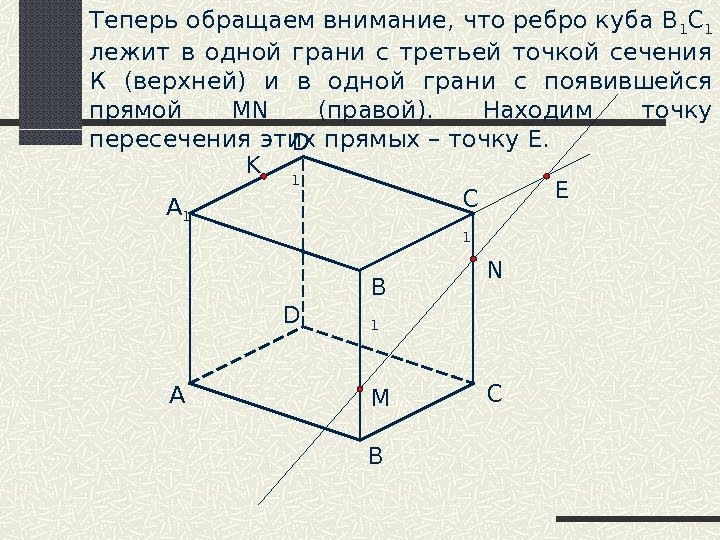
 A B CD B 1 C 1 D 1 M NK A 1 EТеперь обращаем внимание, что ребро куба В 1 С 1 лежит в одной грани с третьей точкой сечения К (верхней) и в одной грани с появившейся прямой MN (правой). Находим точку пересечения этих прямых – точку Е.
A B CD B 1 C 1 D 1 M NK A 1 EТеперь обращаем внимание, что ребро куба В 1 С 1 лежит в одной грани с третьей точкой сечения К (верхней) и в одной грани с появившейся прямой MN (правой). Находим точку пересечения этих прямых – точку Е.
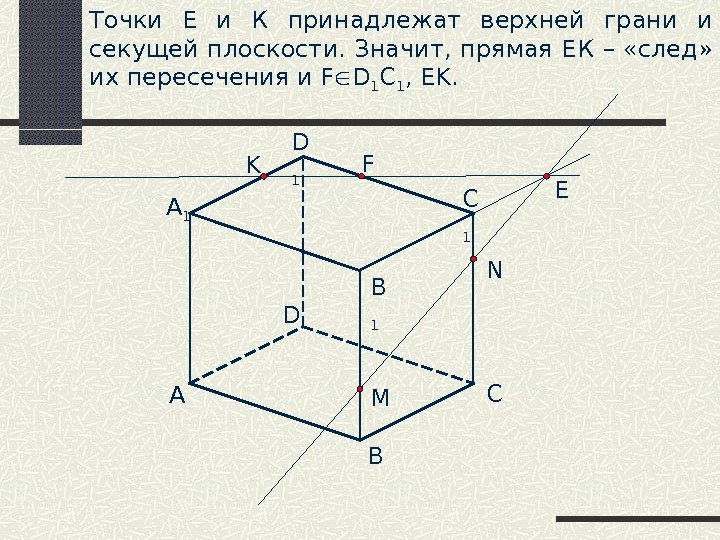
 A B CD B 1 C 1 D 1 M NK A 1 EТочки Е и К принадлежат верхней грани и секущей плоскости. Значит, прямая ЕК – «след» их пересечения и F D 1 C 1 , EK.
A B CD B 1 C 1 D 1 M NK A 1 EТочки Е и К принадлежат верхней грани и секущей плоскости. Значит, прямая ЕК – «след» их пересечения и F D 1 C 1 , EK.
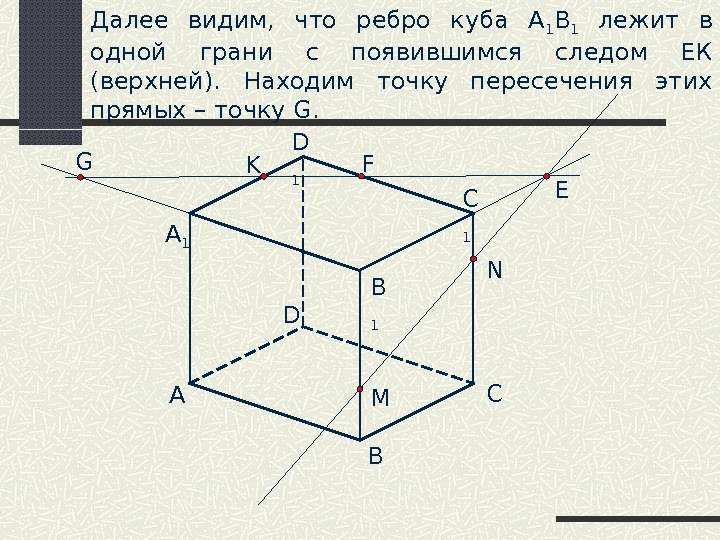
 A B CD B 1 C 1 D 1 M NK A 1 EFДалее видим, что ребро куба А 1 В 1 лежит в одной грани с появившимся следом ЕК (верхней). Находим точку пересечения этих прямых – точку G. G
A B CD B 1 C 1 D 1 M NK A 1 EFДалее видим, что ребро куба А 1 В 1 лежит в одной грани с появившимся следом ЕК (верхней). Находим точку пересечения этих прямых – точку G. G
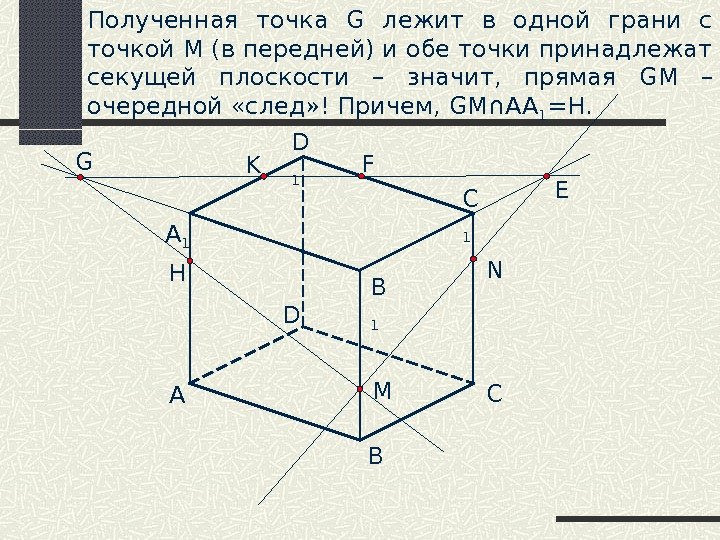
 A B CD B 1 C 1 D 1 M NK A 1 EFG Полученная точка G лежит в одной грани с точкой М (в передней) и обе точки принадлежат секущей плоскости – значит, прямая GM – очередной «след» ! Причем, GM ∩ АА 1 =Н. H
A B CD B 1 C 1 D 1 M NK A 1 EFG Полученная точка G лежит в одной грани с точкой М (в передней) и обе точки принадлежат секущей плоскости – значит, прямая GM – очередной «след» ! Причем, GM ∩ АА 1 =Н. H
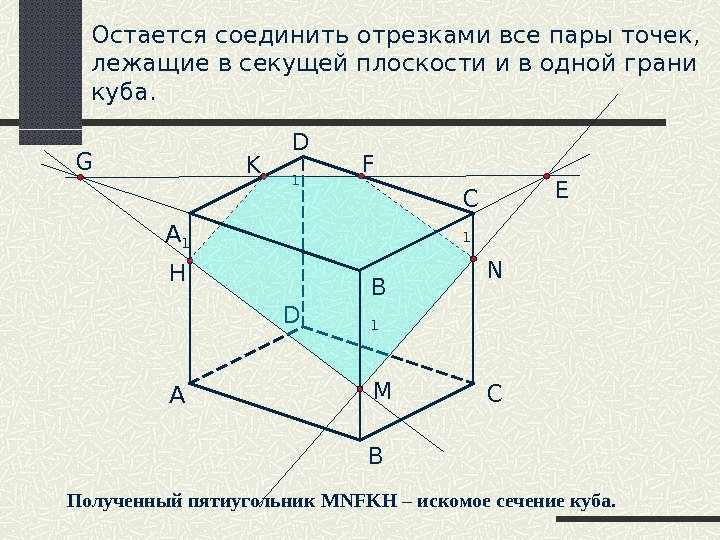
 A B CD C 1 D 1 M NK A 1 EFG HОстается соединить отрезками все пары точек, лежащие в секущей плоскости и в одной грани куба. Полученный пятиугольник MNFKH – искомое сечение куба.
A B CD C 1 D 1 M NK A 1 EFG HОстается соединить отрезками все пары точек, лежащие в секущей плоскости и в одной грани куба. Полученный пятиугольник MNFKH – искомое сечение куба.
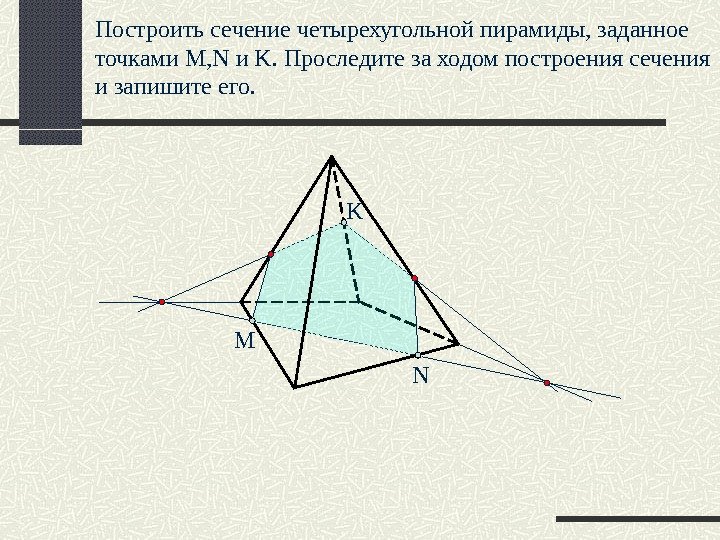
 M NKПостроить сечение четырехугольной пирамиды, заданное точками M, N и K. Проследите за ходом построения сечения и запишите его.
M NKПостроить сечение четырехугольной пирамиды, заданное точками M, N и K. Проследите за ходом построения сечения и запишите его.
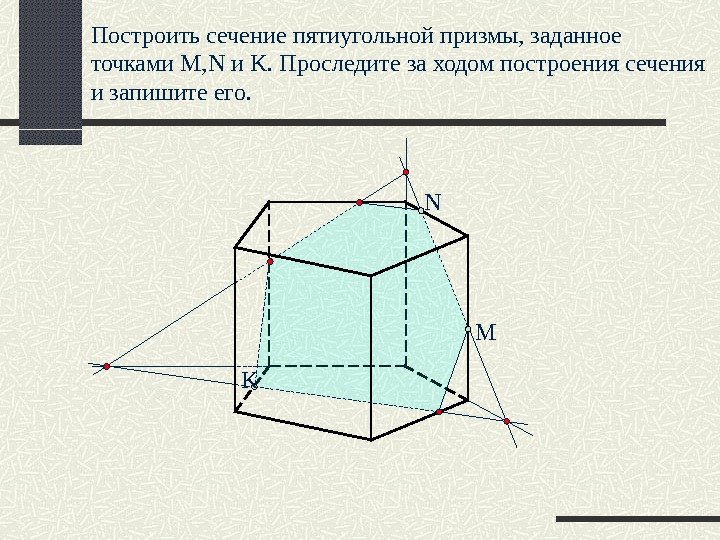
 Построить сечение пятиугольной призмы, заданное точками M, N и K. Проследите за ходом построения сечения и запишите его. MN K
Построить сечение пятиугольной призмы, заданное точками M, N и K. Проследите за ходом построения сечения и запишите его. MN K
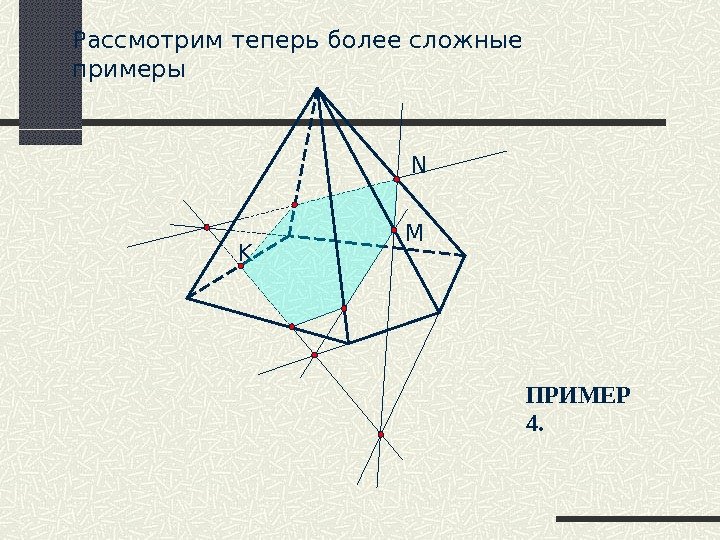
 M N KРассмотрим теперь более сложные примеры ПРИМЕР 4.
M N KРассмотрим теперь более сложные примеры ПРИМЕР 4.
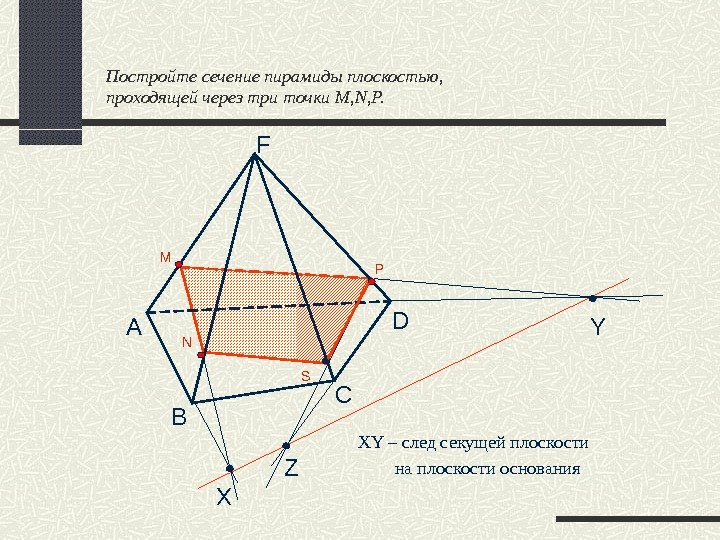
 Постройте сечение пирамиды плоскостью, проходящей через три точки M, N, P. XY – след секущей плоскости на плоскости основания. D C BА Z Y XM N P S
Постройте сечение пирамиды плоскостью, проходящей через три точки M, N, P. XY – след секущей плоскости на плоскости основания. D C BА Z Y XM N P S
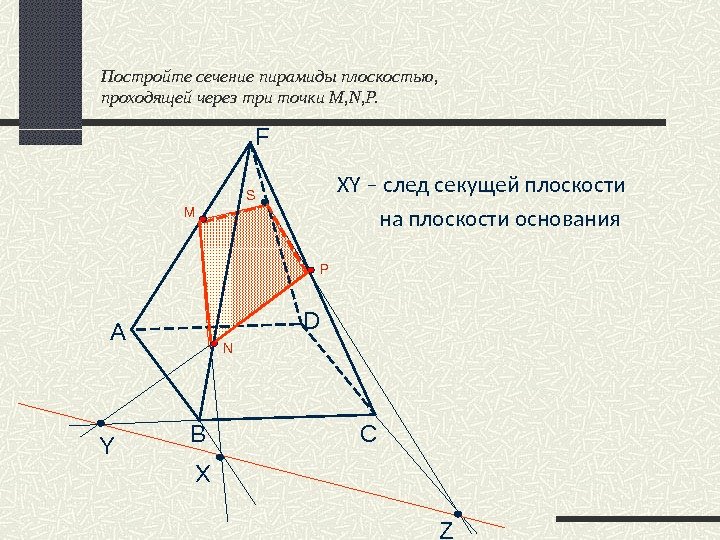
 XY – след секущей плоскости на плоскости основания D CB ZY XM N PSПостройте сечение пирамиды плоскостью, проходящей через три точки M, N, P. А
XY – след секущей плоскости на плоскости основания D CB ZY XM N PSПостройте сечение пирамиды плоскостью, проходящей через три точки M, N, P. А
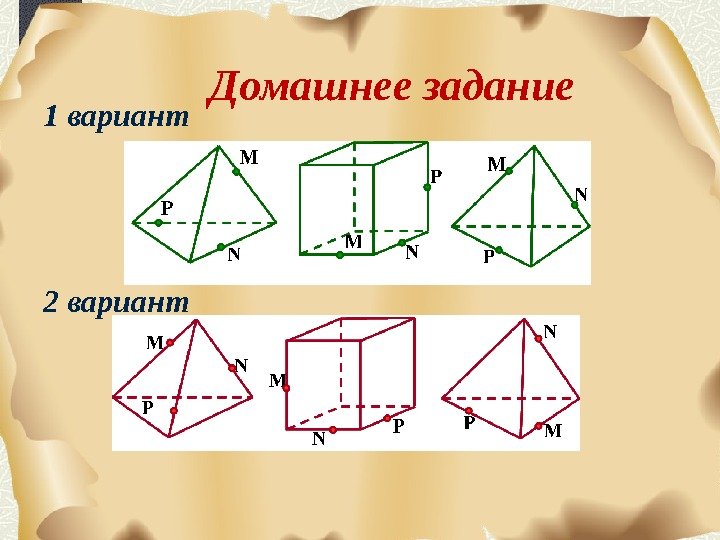
 Домашнее задание 1 вариант 2 вариант
Домашнее задание 1 вариант 2 вариант
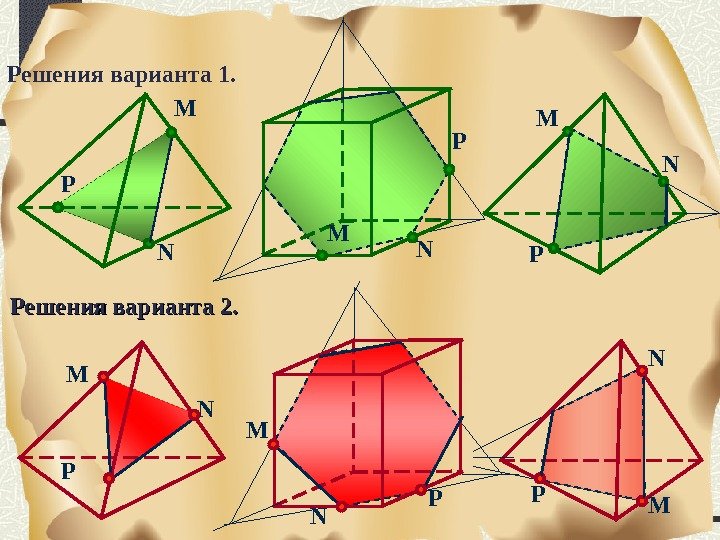
 P NM NP M N P MРешения варианта 1. Решения варианта 2. M N P MN P
P NM NP M N P MРешения варианта 1. Решения варианта 2. M N P MN P

